Algebra 2 by Richard Wright

Previous LessonTable of Contents Next Lesson

Are you not my student and
has this helped you?

2-05 Write Quadratic and Polynomial Models (4.9)

Mr. Wright teaches the lesson.

Objectives:

SDA NAD Content Standards (2018): AII.5.1, AII.5.2, AII.6.5, AII.7.1, AII.7.2

Medical lab
Figure 1: Collecting data in a medical lab. (Pixabay/Belova59)

Equations that model real life situations do not just magically appear out of thin air. In real life situations, people need to collect data which can plotted as points on a graph. Mathematical modeling turns those points into a function that models that situation.

Mathematical Modeling

Mathematical modeling is the process of finding a function that best fits the given points or data.

Find a Polynomial Model Given x-intercepts

In lesson 2-02, instructions were given to find a quadratic model given the x-intercepts and another point. The same idea can be used to write general polynomial models given the x-intercepts and one other point.

  1. Write a polynomial model in the form y = a(x – k1)(x – k2)(x – k3)… where there is one factor per x-intercept.
  2. Substitute the x-intercepts for the k's.
  3. Substitute the other point for x and y.
  4. Solve for a.
  5. Write the polynomial function.

Example 1

Write a polynomial model with x-intercepts (−2, 0), (1, 0), and (5, 0) and passes through (2, 4).

Solution

There are three x-intercepts so write the general polynomial with three factors.

y = a(x – k1)(x – k2)(x – k3)

Substitute the x-intercepts for the k's.

y = a(x – (–2))(x – 1)(x – 5)

y = a(x + 2)(x – 1)(x – 5)

Substitute the other point for x and y.

4 = a(2 + 4)(2 – 1)(2 – 5)

4 = a(–18)

$$ -\frac{2}{9}=a $$

Finally, write the function by substituting the x-intercepts and a into the general polynomial model.

$$ y=-\frac{2}{9}\left(x+4\right)\left(x-1\right)\left(x-5\right) $$

General Polynomial Models

If none of the special points, vertex or x-intercepts are given, then the process is a little longer. The first step is to determine the degree of the function. If the function is to through all the points, then the process of finding finite differences will show the degree.

Find the Degree of a Polynomial Using Finite Differences

To find the degree of a function using finite differences,

  1. Have a table of values with equally spaces x-values.
  2. Find the differences of successive y-values.
  3. Find the differences of successive differences from the previous step.
  4. Repeat until all the differences in a step are the same number (not zero).
  5. The number of levels of differences is the degree of the function.

Example 2

Find the degree of the polynomial function passing through (0, −4), (1, −4), (2, −2), (3, 8), (4, 32), (5, 76), (6, 146).

Solution

Write the points as a table.

x 0 1 2 3 4 5 6
y −4 −4 −2 8 32 76 146

Subtract the y-values.

x0123456
y−4−4−283276146
\/\/\/\/\/\/
0210244470

Subtract those differences.

x0123456
y−4−4−283276146
\/\/\/\/\/\/
0210244470
\/\/\/\/\/
28142046

Subtract those differences.

x0123456
y−4−4−283276146
\/\/\/\/\/\/
0210244470
\/\/\/\/\/
28142046
\/\/\/\/
6666

These differences are all the same. It took three levels of subtracting for the differences to be constant, so the degree of the function is 3.

To find a polynomial function that passes through given points,

  1. Use finite difference to find the degree.
  2. Use either of the following methods.

      3. Method 1: Solve a System of Equations by Hand (This lesson uses Method 2)

      Figure 2: Regression in TI-84
      1. Write a general polynomial function of the given degree such as y = ax3 + bx2 + cx + d.
      2. Substitute a point for x and y to get an equation where the variables are the coefficients.
      3. Substitute another point in the general polynomial for x and y to get a second equation where the variables are the coefficients.
      4. Continue substituting points until there the same number of equations as coefficients.
      5. Solve the system of equations using something like elimination to find the values of the coefficients.
      6. Write the equation by substituting the coefficients into the general polynomial.

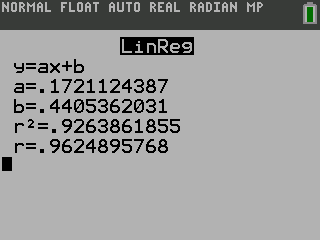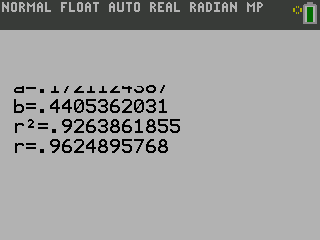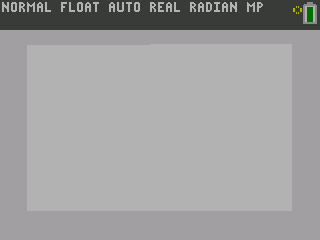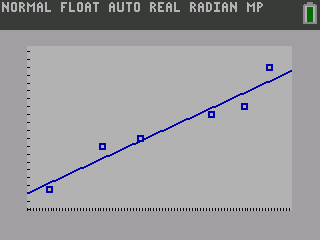
      Method 2: Use a Regression on a Graphing Calculator

      Figure 3: Regression in NumWorks
      1. Finding Linear Regression on a TI-84
        1. Push STAT and select Edit….
        2. Enter the x-values in List 1 (L1) and the y-values in List 2 (L2).
        3. To see the graph of the points
          1. Push Y= and clear any equations.
          2. While still in Y=, go up and highlight Plot1 and press ENTER.
          3. Press ZOOM and select ZoomStat.
        4. Push STAT and move over to the CALC menu.
        5. Select the type of regression.
        6. Make sure the Xlist: is L1, the Ylist: is L1, the FreqList: is blank, and the Store RegEQ: is Y1.
          1. Get Y1 by pressing VARS and select Y-VARS menu.
          2. Select Function….
          3. Select Y1.
        7. Press Calculate
        8. The calculator will display the equation. To see the graph of the points and line, press GRAPH.

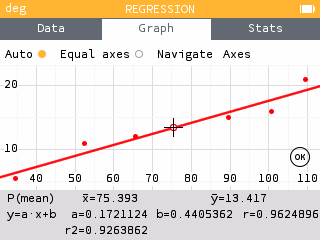
          9. Note: Older TI graphing calculators do not have the screen in steps 6 and 7. After selecting the LinReg(ax+b), the screen just shows "LinReg(ax+b)". Press ENTER again to see the result. To see the graph, enter the equation into the Y= screen and press GRAPH.

      2. Finding Linear Regression on a NumWorks graphing calculator
        1. On the home screen select Regression.
        2. In the Data tab, enter the points.
        3. Move to the Graph tab.
        4. The default is a linear regression and is displayed at the bottom of the screen. To change the regression type
          1. Press OK.
          2. Select Regression.
          3. Select the desired regression type.

Example 3

Find the polynomial function passing through the (0, −4), (1, −4), (2, −2), (3, 8), (4, 32), (5, 76), (6, 146).

Solution

These are the same points as example 2, so the degree is 3. This example will illustrate method 2: using a graphing calculator to do a regression.

TI-84 NumWorks

Push STAT and select Edit…

Enter the x-values in List 1 (L1) and the y-values in List 2 (L2).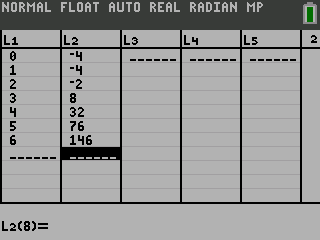

Figure 4: Stat table in TI-84

Push STAT and move over to the CALC menu.

Select the type of regression.

Make sure the Xlist: is L1, the Ylist: is L1, the FreqList: is blank, and the Store RegEQ: is Y1.

Get Y1 by pressing VARS and select Y-VARS menu.

Select Function….

Select Y1.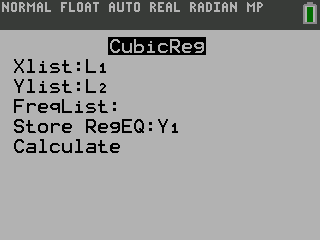

Figure 5: Regression screen in TI-84

Press Calculate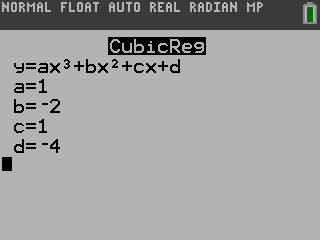

Figure 6: Regression results in TI-84

On the home screen select Regression.

In the Data tab, enter the points.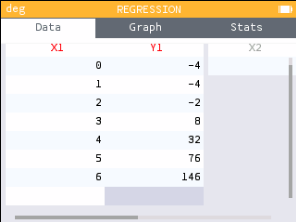

Figure 7: Stat table in NumWorks

Move to the Graph tab.

The default is a linear regression and is displayed at the bottom of the screen. To change the regression type

  1. Press OK.
  2. Select Regression.
  3. Select the desired regression type.
Figure 8: Regression in NumWorks
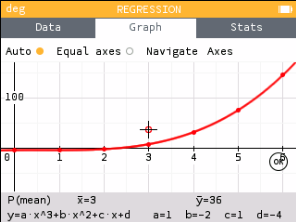
Both calculators say that a = 1, b = −2, c = 1, and d = −4. Substitute those into the general polynomial function given on the calculator. The polynomial function through those points is y = x3 − 2x2 + x − 4.

Example 4

Find the polynomial function through (0, −16), (1, −10.5), (2, −4), (3, 3.5), (4, 12), (5, 21.5), (6, 32).

Solution

Because these are not special points, use finite differences to find the degree.

x0123456
y−16−10.5−43.51221.532
\/\/\/\/\/\/
5.56.57.58.59.510.5
\/\/\/\/\/
11111

There were two levels of finite differences, so the degree is 2 so it is quadratic.

Use technology to find the quadratic function.

Figure 9: Regression in NumWorks

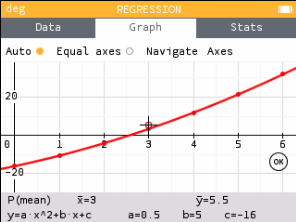
The polynomial function through the points is y = 0.5x2 + 5x − 16.

Finding Best-Fitting Polynomial Models

Finite differences do not work to find the degree of the polynomial for data measured many experiments or studies. This is because many situations do not have an exact model, just an approximation. These situations use a regression which is a calculated best-fitting model.

To find the best-fitting polynomial model using a graphing calculator, use method 2 from above. It may be necessary to try a couple different degrees to find the best fit. For example, the cubic may be close, but the quartic might be closer.

Example 5

Find the best-fitting polynomial model for the population of Michigan given in the table. Then estimate the population in 2050.

Year 1900 1910 1920 1930 1940 1950 1960 1970 1980 1990 2000 2010
Population (millions) 2.42 2.83 3.72 4.83 5.32 6.41 7.83 8.88 9.21 9.31 9.92 9.93

Use the number of years after 1900 as the x-coordinate. It is usually called t for time. The population is y. Notice population is in millions.

Enter the data in the STAT or Regression table.

Figure 10: Data table in NumWorks

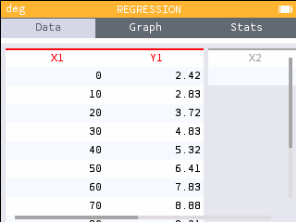
Try several regressions to see which is best.

Figure 11: Quadratic Regression
Figure 12: Cubic Regression
Figure 13: Quartic Regression

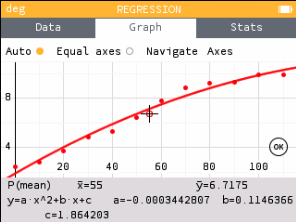
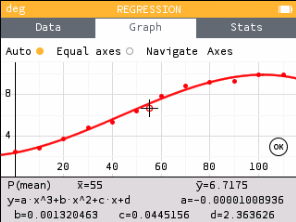
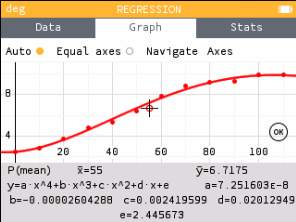
Notice that the cubic seems to fit better than the quadratic. Also notice that the quartic and cubic look almost identical. When that happens use the lower degree. Thus, this situation should use the cubic model.

y = −0.0000101x3 + 0.00132x2 + 0.0445x + 2.364

Substitute more meaningful variables for x and y. Use t for x and P for y.

P = −0.0000101t3 + 0.00132t2 + 0.0445t + 2.364

To estimate the population in 2050, substitute t = 150.

P = −0.0000101(150)3 + 0.00132(150)2 + 0.0445(150) + 2.364

P = 4.65

The population would be 4.65 million if this trend continues. Since this is half of the population in 2000 and 2010 and population tends to grow over long periods of time, this model is likely not valid for 2050.

Practice Problems

217 #1, 3, 5, 7, 9, 11, 13, 14, 17, 19, Mixed Review = 15

    Mixed Review

  1. (2-04) Graph y = (x − 3)(x − 1)(x + 1) and identify the x-intercepts.
  2. (2-04) Use the graph to estimate the turning points.
  3. (2-03) Write an inequality for the graph.
  4. (2-02) Find the quadratic model with x-intercepts 3 and 5 and passes through (4, 3).
  5. (2-01) Find the quadratic model with vertex (2, −5) and passes through (0, 3).

Answers

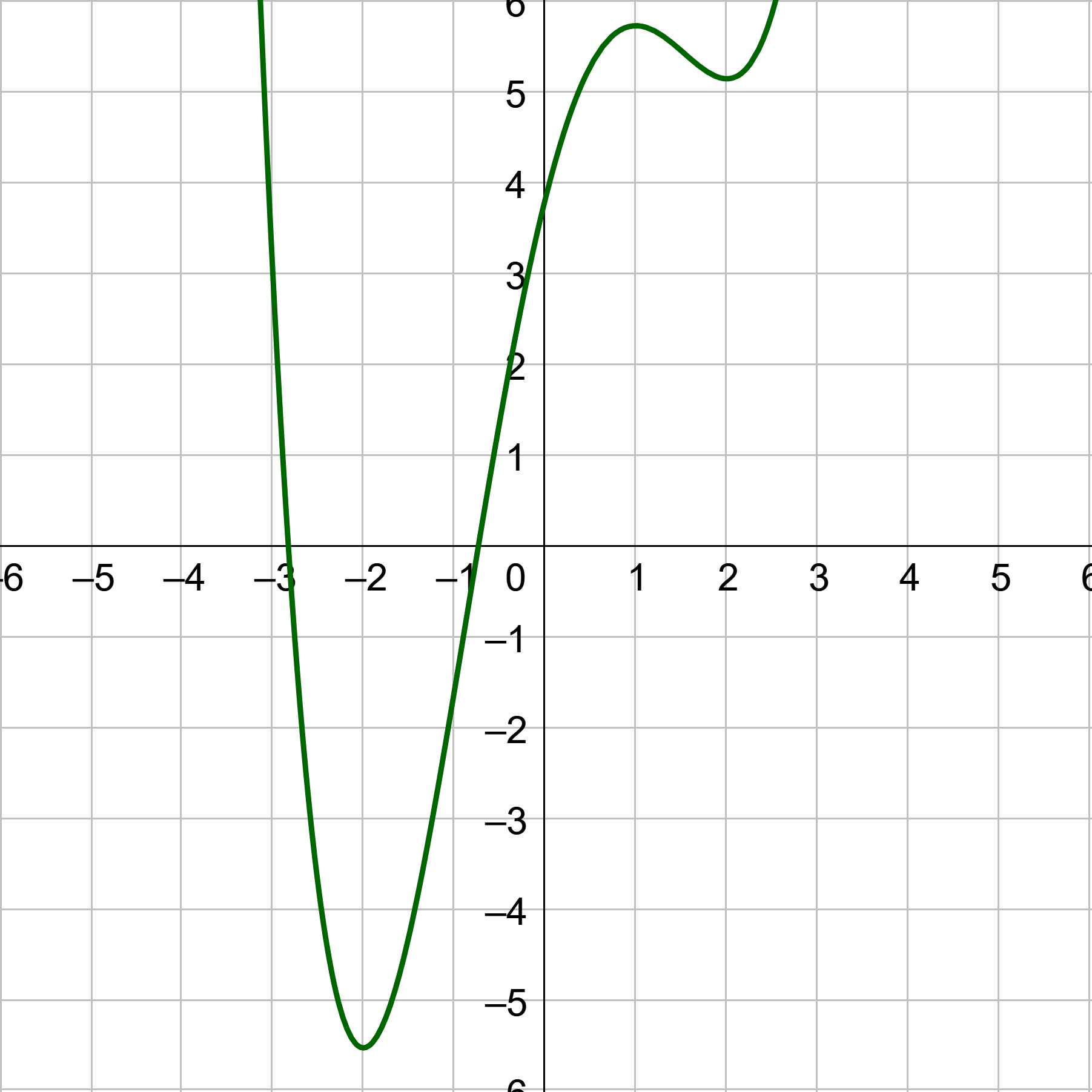
  1. ; (−1, 0), (1, 0), (3, 0)
  2. Minimums: (−2, −5.5) and (2, 5.1); Maximum: (1, 5.7)
  3. y ≤ x2 − 4
  4. y = −3(x − 3)(x − 5)
  5. y = 2(x − 2)2 − 5