Abstract

Within this lab, we studied Ohm's law on simple circuits and verified the rules that we use to combine resistors. In parts 5 and 6, we created several complex circuits, and used Kirchhoff's laws to determine the currents through different arms of the circuit. The lab turned out to be an epic success, and there was much merriment.

Contents

• Abstract
• Objectives
• Methods
• Setup
• Data and Analysis
• Conclusion
• Signature

Objectives

• To study the relationship between current and voltage in DC circuits.
• To observe resistance, current, and voltage relationships in series and parallel combinations.

Methods

Part 1: Resistance in series:

We will connect three resistors with values of about 2200Ω, 3300Ω, and 4700Ω in series as shown in figure 3. We will record a table of nominal and measured resistance values, and calculate the percent deviation. This table will include rows for R1, R2, R3, R1+R2, R2+R3, and R1+R2+R3.

Part 2: Voltage for resistors in series:

We will plug the banana leads of two breadboard leads into the positive and negative receptacles on the power supply. The wires will then be put into a breadboard across the three resistors in series with an ammeter shown in figure 3. The voltage will be set to about 15 volts. The voltage will be measured and recorded for R1, R2, R3, R1+R2, R2+R3, and R1+R2+R3. These resistances will be compared to the products of the current and the corresponding resistance values to obtain percentage errors.

Part 3: Resistance in parallel:

Three resistors will be connected in parallel. We will measure the resistance of the three resistances in parallel and compare it to 1/Req=1/R1+1/R2+1/R3.

Part 4: Current for resistors in parallel:

We will connect a power supply to the parallel combination of the three resistors. The voltage will be set to 15 volts, and the meters will be set to measure the resistance, and I1, I2, and I3. A table will be kept with resistance, voltage, and current. We will compare V/R to I for each of the rows in the table.

Part 5: Complex Circuit:

We will setup the following circuit and compare the calculated and measured equivalent resistance of the resistor network.

Circuit schematic

We will then connect the battery to the resistor network and measure the voltage drop and current through each resistor. In a table, the measured and calculated values will be compared, and a column for the power dissipated by each resistor will be kept.

Part 6: Kirchoff's Law Circuit

Using 3 resistors with values of 2200Ω, 3300Ω, and 4700Ω, the circuit in figure 5 will be built. The values of V1, V2, I1, I2, and I3 will be recorded, and compared with theoretical values found by Ohm's Law and Kirchoff's Laws. The values of I1, I2, and I3 are determined theoretically from the three equations:

The first equation is the current law, the second is the voltage law applied to the left side of the loop and the third is the voltage law applied to the right side of the loop. By solving these equations, one can arrive at theoretical values for the data.

Setup

Materials:

• 2 Digital multimeters
• 2 DC power couples, 0-15V
• Assorted Resistors
• Circuit boards, circuit board leads
• Graphical Analysis and mathcad software

Data and Analysis

Part 1

Data and analysis for part 1

	Resistance(Ohms)	Voltage(V)	Current(mA)	Experimental Resistance (Ohms)	Percent Error
R1	2200	4.94	2.14	2308	4.93%
R2	3300	4.95	1.49	3322	0.67%
R3	4700	4.87	0.977	4985	6.06%
R1+R2	5500	4.89	0.868	5634	2.43%
R2+R3	8000	4.96	0.591	8393	4.91%
R1+R2+R3	10200	4.93	0.464	10625	4.17%

Part 2

Data and analysis for part 2

	Resistance(Ohms)	Battery Voltage (V)	Current(mA)	Theoretical Voltage Drop(V)	Experimental Resistance (Ohms)	Percent Error
R1	2200	15	1.41	3.10	3.25	4.77%
R2	3300	15	1.41	4.65	4.69	0.80%
R3	4700	15	1.41	6.63	7.03	6.08%
R1+R2	5500	15	1.411	7.76	7.94	2.31%
R2+R3	8000	15	1.411	11.29	11.73	3.92%
R1+R2+R3	10200	15	1.412	14.40	14.99	4.08%

Part 3

By using the following equation, we can determine the theoretical equivalent resistance of three resistors in parallel.

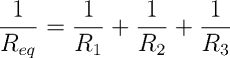
If R1=2200Ω, R2=3300Ω, and R3=4700, any modern scientific calculator with a competent user will arrive at a R_eq value of R_eq=1031Ω.

Data and analysis for part 3

Voltage	Current	Experimental Resistance(Ohms)	Theoretical Resistance(Ohms)	Percent Error
14.99	14.03	1068	1031	3.67%

Part 4

Data and analysis for part 4

Resistor	Resistance(Ohms)	Voltage(V)	Power Experimental(mW)	Current(mA)	Theoretical Current(mA)	Percent Error
R1	2200	14.98	98	6.53	6.81	4.10%
R2	3300	14.98	68	4.54	4.54	0.01%
R3	4700	14.98	45	3.02	3.19	5.25%
Total	1031	14.98	210	14.02	14.54	3.55%

Part 5

Circuit schematic

Photo of our setup

Data and analysis for part 5

Resistor(Ohms)	Voltage Drop(V)	Current(mA)	Experimental Resistance(Ohms)	Theoretical Resistance(Ohms)	Percent Error
R1(1500)	4.72	3.15	1498	1500	0.11%
R2(2200)	4.72	2.04	2314	2200	5.17%
R3(4700)	10.39	2.08	4995	4700	6.28%
R4(3300)	10.39	3.12	3330	3300	0.91%
R1+R2	4.72	5.19	909	892	1.97%
R3+R4	10.39	5.19	2002	1939	3.26%
R1+R2+R3+R4	15.13	5.19	2915	2831	2.99%

Part 6

Photo of our setup

Schematic diagram

V1=5.00V
V2=10.00V
R1=2220Ω
R2=3300Ω
R3=4700Ω

Rather than dealing with all the algebra, we decided to solve this with a matrix, so here it is.

Which reduces to

Data and analysis for part 6

	Theoretical(mA)	Experimental(mA)	Percent Error
Current 1	-2.91	-2.78	4.47%
Current 2	1.09	1.06	2.75%
Current 3	1.83	1.71	6.56%

Conclusion

The lab was a success. Ohm's laws, the rules for combining resistors in series and parallel, and Kirchhoff's rules for voltage and current were all supported very well by our data. Oh, of only the great Gustav Kirchhoff and Georg Ohm were here with us in the laboratory for this most exciting experiment. The beauty of our circuits, and the accuracy of our experiments would no doubt bring a tear of joy to their eyes.

As mind-bogglingly amazing and accurate and wonderful this lab was, there was still some error in this lab. Possible sources include the destructive and wicked forces of internal resistance. These wonderful wires that our fearless TA's provided us were certainly very willing to transmit current without much resistance, but sadly, even these wires had some resistance. Not 100% of the resistance in our setup was in the resistors, and our equations did not account for this. It is also unfortunate (at least in the context of the accuracy of this experiment) that resistance increases with an increase in temperature. As current was running through our setup, the resistors warmed up, and their resistances increased. This means that as we were measuring the current through other resistors, the current was changing as the resistance was changing in the other parts of the circuit.

It was a delight to perform this glorious experiment. I was overcome by the beauty of it all every time I plugged a lead into the breadboard. The lab, as it exists, is very thorough and illustrates electrical principles very nicely. But in order to illustrate these principles even more nicely, it might be good to hook up six multimeters simultaneously to the circuit, so one could take in all the data (and beauty) simultaneously. Other than that though, I believe the lab was very free of errors.

Signature