Back to the Table of Contents
A Review of Basic Geometry—Activity 2
More Topological Abnormalities
Remember that topologically, a single-handled mug is equivalent to
a torus (doughnut). Now take a piece of string or yarn and tie
it in the fashion indicated below left to the handle of a mug. Have someone
hold the string and another person take the cup off the string through
the knot (i.e. while the first person hold both ends of the string).
Is the string really tied to the cup. Now reverse the process.
Interesting!
Pictured above right is only one example of readily encountered
puzzles loosely based on this same principle.
The goal is to move the nut from one loop to the other without
untying the knot at either end.
If you make your own wooden puzzle like the one above,
be sure the nut or washer is too large
to fit through the hole and please use two nuts/washers.
The goal then is to split them,
which is much easier to verify then moving it from one side to the other.
Here is yet another puzzle application for this problem.
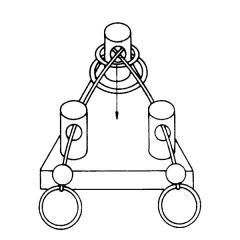
|
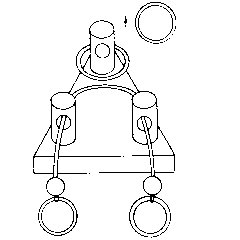
|
| Three Post puzzle--Start
| Three Post puzzle--End
|
Having solved the above puzzles can we apply what we have learned
to another situation?
This interesting topological problem makes for an interesting party game.
Select a pair from each table group and see if you can help them find the
solution for becoming untangled. (See figure below.)
Here are yet some more puzzles loosely based on these same principles.
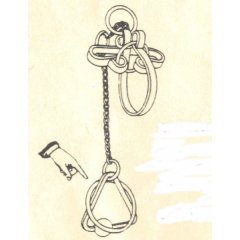
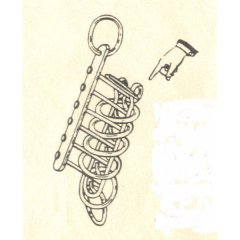
| 
| 
|
| Sneaky Pete
| Chinese Rings or Torture
| Horseshoe Puzzle
|
I had forgotten how to solve Sneaky Pete and lost the instructions.
However, this web site
was recently e-mailed to me.
Please note it does not ever need to be forced and actually we have
had to have the rings welded shut because students abused it.
Please do not force it.
However, if you solve it, please let me know.
The Chinese Rings are one of my favorite puzzles.
I discovered this one when I was 15 years old.
It was made out of coat hanger wire.
I was instantly hooked!
There seems to be a binary pattern to it.
Can you describe
it?
Here is another
view.
The "original" horseshoe puzzle is also a fun one.
![[single-handled mug with loop knot around handle]](cupstrng.jpg)
![[small wooden board with three holes, string loop tied in center hole, tied each end, and pair of large washers on strong]](strngtoy.jpg)
![[single-handled mug with loop knot around handle]](cupstrng.jpg)
![[small wooden board with three holes, string loop tied in center hole, tied each end, and pair of large washers on strong]](strngtoy.jpg)


![[boy and girl each with strings joining own wrists, looped]](partygam.jpg)


