Back to the Table of Contents
A Review of Basic Geometry - Lesson 13
Similar Triangles and An Intro. to Trigonometry
Lesson Overview
Last chapter
we introduced the similarity transformation and
this chapter we will apply it more specifically to triangles.
Similarity between triangles is the basis of trigonometry,
which literally means triangle measure.
As noted in Numbers lesson 11,
the trigonometric functions can be thought of as
ratios of the side lengths in right triangles.
Please review the informative paragraph and table of special
trigonometric values given there.
If three sides of a triangle are proportional to the three sides of another triangle,
then the triangles are similar (SSS Similarity Theorem).
|
If the angles (two implies three) of two triangles are equal,
then the triangles are similar (AA Similarity Theorem).
|
Note: this applies not only to ASA, AAS=SAA, but also to AAA situations.
If two sides of a triangle are proportional to two sides of another
triangle and the
included angles are congruent, then the triangles
are similar (SAS Similarity Theorem).
|
Thus remains the SSA (ASS) case, which remains
ambiguous
unless HL or SsA occurs.
Lines parallel to a side of a triangle intersect the other two sides at nonvertices,
if and only if the two sides are split into proportional segments.
|
Since this theorem is given as an if and only if, it goes both ways.
Thus the textbook has both a theorem and its converse.
We introduced the geometric mean somewhat in the
last chapter and
somewhat in statistics.
Please review what we have there.
The geometric mean is typically first encountered in a
proportion
when the means are equal, as in 8/w=w/4. Here w2=32
and square rooting both sides gives an answer. However, in general,
there may be n nth geometric means.
We thus cannot be sure of the sign of w above.
The geometric mean is developed here because of its application to right
triangles and the way the altitude to the hypotenuse divides the triangle
into similar triangles.
Assume you have two of the three terms in a geometric sequence,
such as 2, ?, 50. In other words, you want some number g,
such that 2/g=g/50, or 2•50=100=g2,
so obviously, g=10 or perhaps g=-10. Often the positive
geometric mean is required and will be so specified.
 The use of lower case letters a, b, and c for the
sides of a triangle is a common convention dating back to Euler
which we will adhere to.
a refers either to the set of points composing the side or the
length of the side, depending on context. The angle opposite side a
is A, the angle opposite side b is B, and the angle
opposite side c is C. If it is a right triangle,
C will be right so c will be the [length of the] hypotenuse.
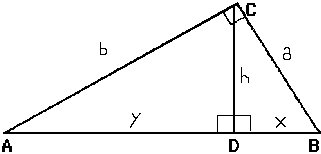
Given the right triangle ABC with height h (CD) to
the hypotenuse, h=
The use of lower case letters a, b, and c for the
sides of a triangle is a common convention dating back to Euler
which we will adhere to.
a refers either to the set of points composing the side or the
length of the side, depending on context. The angle opposite side a
is A, the angle opposite side b is B, and the angle
opposite side c is C. If it is a right triangle,
C will be right so c will be the [length of the] hypotenuse.
Given the right triangle ABC with height h (CD) to
the hypotenuse, h=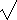 (xy),
whereas a=
(xy),
whereas a=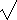 (cx),
and b=
(cx),
and b=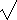 (cy).
Here x+y=c (BD + AD = AB),
and y is the leg of a similar triangle with hypotenuse b,
and x is the leg of a similar triangle with hypotenuse a.
(cy).
Here x+y=c (BD + AD = AB),
and y is the leg of a similar triangle with hypotenuse b,
and x is the leg of a similar triangle with hypotenuse a.
The altitude of a triangle is the geometric mean of the segments of the
hypotenuse that it divides.
Each leg would also be a geometric mean of
the hypotenuse and the adjacent segment of the hypotenuse.
|
An isosceles right triangle (45°–45°–90°)
is a very special triangle.
Its side lengths form a very special ratio which must be memorized.
Specifically, if the legs are both of length x, then the
hypotenuse is of length 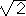 x by the
pythagorean theorem. This ratio of 1/
x by the
pythagorean theorem. This ratio of 1/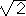 =
=
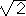 /2 or about 0.707 must become familiar.
/2 or about 0.707 must become familiar.
Similarly, the 30°–60°–90°
triangle must be memorized, somehow. One way is to start with an
equilateral triangle, bisect one angle which also bisects the side opposite,
and consider the resulting congruent triangles.
Obviously, two congruent 30°–60°–90°
triangles are formed. Again, by the pythagorean theorem, the side length
ratios can be found to be 1: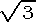 :2.
By the AA Similarity Theorem, any triangle with these angles has these
exact side length ratios.
:2.
By the AA Similarity Theorem, any triangle with these angles has these
exact side length ratios.
In right triangles, the six side length ratios are
proportional to the angles and named as follows.
sin A = opposite leg ÷ hypotenuse
csc A = hypotenuse ÷ opposite leg
cos A = adjacent leg ÷ hypotenuse
sec A = hypotenuse ÷ adjacent leg
tan A = opposite leg ÷ adjacent leg
cot A = adjacent leg ÷ opposite leg
|
Various mnemonics are commonly employed to assist in the recall of these ratios.
SOH-CAH-TOA, with some apocryphal reference to a so named Indian chief is
common: S=Sine, O=Opposite, H=Hypotenuse, C=Cosine, A=Adjacent, T=Tangent.
Oh Hech Another Hour Of Algebra is another similar mnemonic.
Another one only recently brought to my attention is: OHAHOAAO, which is
short for Oscar Had A Hand On Alice's Arch Once, which gives, in order,
the ratios for Sine, Cosine, Tangent, and Cotangent.
Note how the right hand column reciprocates the left hand column.
For this reason, the left hand column are considered the primary
trigonometric functions and the right hand column secondary.
Most calculators only have the primary trig functions.
Consider a right triangle with c=1, one vertex at the origin,
one side along the x-axis, and the right angle formed by a
perpendicular to the x-axis, thus the hypotenuse lies in quadrant I.
In this case we often label one leg y and the
other leg x. Consider what happens as we let the angle
at the origin change. As the angle increases, the side opposite
increases. Since we fixed c=1, that vertex traces out a
portion of a unit circle. The sine function describes how this
side changes with angle, starting at 0 for 0° and
increasing monotonically to 1 for 90° (of course
at 0° and 90° it really isn't a triangle).
Similarly, the cosine function, which describes how the adjacent side
varies, starts out at 1 for 0° and
is always decreasing to 0 for 90°.
Tangent is not only the ratio of the opposite side to the adjacent
side, but can also be written as sine over cosine.
If cosine equals 0, we have a problem, division by zero,
so the tangent of 90° is undefined.
Large tables of trig functions were commonplace before calculators
became ubiquitous. Below is a small table in 5°
increments between 0° and 90°.
Notice how the cosine values are the same as the sine values
of the complementary angle. Tangent and cotangent are similarly related.
A later lesson will extend these trig functions past a right angle,
into negative angles, graph them,
and reintroduce the unit circle.
Angle
(degrees) | Angle
(radians) | Sine | Cosine | Tangent | Cotangent | Secant | Cosecant
|
|---|
| 0 | 0 | .0000 | 1.0000 | .0000 | NAN | 1.0000 | Infinite
|
| 5 |  /36 /36 | .0872 | .9962 | .0875 | 11.4301 | 1.0038 | 11.4737
|
| 10 |  /18 /18 | .1736 | .9848 | .1763 | 5.6713 | 1.0154 | 5.7588
|
| 15 |  /12 /12 | .2588 | .9659 | .2679 | 3.7321 | 1.0353 | 3.8637
|
| 20 |  /9 /9 | .3420 | .9397 | .3640 | 2.7475 | 1.0642 | 2.9238
|
| 25 | 5 /36 /36 | .4226 | .9063 | .4663 | 2.1445 | 1.1034 | 2.3662
|
| 30 |  /6 /6 | .5000 | .8660 | .5774 | 1.7321 | 1.1547 | 2.0000
|
| 35 | 7 /36 /36 | .5736 | .8192 | .7002 | 1.4281 | 1.2208 | 1.7434
|
| 40 | 2 /9 /9 | .6428 | .7660 | .8391 | 1.1918 | 1.3054 | 1.5557
|
| 45 |  /4 /4 | .7071 | .7071 | 1.0000 | 1.0000 | 1.4142 | 1.4142
|
| 50 | 5 /18 /18 | .7660 | .6428 | 1.1918 | .8391 | 1.5557 | 1.3054
|
| 55 | 11 /36 /36 | .8192 | .5736 | 1.4281 | .7002 | 1.7434 | 1.2208
|
| 60 |  /3 /3 | .8660 | .5000 | 1.7321 | .5774 | 2.0000 | 1.1547
|
| 65 | 13 /36 /36 | .9063 | .4226 | 2.1445 | .4663 | 2.3662 | 1.1034
|
| 70 | 7 /18 /18 | .9397 | .3420 | 2.7475 | .3640 | 2.9238 | 1.0642
|
| 75 | 5 /12 /12 | .9659 | .2588 | 3.7321 | .2679 | 3.8637 | 1.0353
|
| 80 | 4 /9 /9 | .9848 | .1736 | 5.6713 | .1763 | 5.7588 | 1.0154
|
| 85 | 17 /36 /36 | .9962 | .0872 | 11.4301 | .0875 | 11.4737 | 1.0038
|
| 90 |  /2 /2 | 1.0000 | .0000 | NAN | .0000 | Infinite | 1.0000
|
Note especially NAN for tan 90°=cot 0°.
NAN is FORTRANese for Not A Number.
It may look like it approaches positive infinity, but since it will approach
negative when approaching 90° from above, and since
the two limits do not agree, we say it is not a number or undefined.
Example: Consider a flagpole, set precisely perpendicular to the ground,
which casts a shadow 11.3355m long and the angle from the ground up at the tip of
the shadow to the tip of the pole is 34.5543°.
What is the height of the flagpole to correct significance?
Solution: Tangent is the ratio of the side opposite the given angle
to the side adjacent, thus tan 34.5543°=h/11.3355m.
Solving for h we obtain h=11.3355m•tan 34.5543°=7.80650m.
If you obtained a negative answer, change your calculator to degrees mode!
The area of any triangle can be found by splitting it into two right triangles.
|
Area of a triangle = (1/2)ab•sin C,
where C is the angle between sides a and b.
|
Math and physics often classify objects by dimensionality, with
scalars (magnitude only) and vectors (magnitude plus direction)
occupying the bottom rungs. A classic physics example involves
speed (a scalar) and velocity (a vector)–speed tells how fast
an object is going, but not in what direction.
One way to develop vectors uses the cartesian coordinate system
and ordered pairs or triples. A vector is then defined by the
directed line segment from the origin to the given point.
The end at the origin is the tail, whereas the other
end is the head and often an arrowhead it put there.
This gives a certain direction between [0°,360°)
and a certain magnitude or length which can be calculated via the
distance formula. The vector represented by the directed line segment
between (0,0) and (3,4) is the same as the one between (1,1) and (4,5),
however, since these have the same magnitude and direction.
We often say we can move the vector around as long as we don't change
the direction it points or its length.
We often break vectors down into x, y, and z
components, especially using sines and cosines for the y and
x components. Unit vectors, vectors of length 1,
especially in the x, y, and z directions are
also utilized. There are special names for these:
i=(1,0,0), j=(0,1,0), and k=(0,0,1).
A unit vector in another direction, such as v=(1,1,1) can be obtained
by dividing this vector by its length designated by |v|:
(1,1,1)/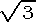 , where it is understood that the scalar
applies to all components of the ordered triple.
, where it is understood that the scalar
applies to all components of the ordered triple.
Vectors are said to be added head to tail, or if given
in component form, via the components. Thus the sum of the vectors
(x1, y1, z1) and
(x2, y2, z2) is the
vector:
(x1+x2, y1+y2,
z1+z2).
Pictorally, the sum is the diagonal of the parallelogram formed by
adding them in either order. [make diagram]
The direction of a 2-D vector can be obtained from its x and y
components. Specifically, the tangent of the angle relative to the x-axis
is equal to y/x. Your calculator has a special key
tan-1, better known as atan,
to find this arctangent or inverse function.
DO NOT confuse this with reciprocal.
(It must become clear to you by context whether arctangent or cotangent is meant.)
Some adjustment of the calculated value will become necessary since
results for quadrants I and IV are assumed.
Since our textbook restricts angles to between 0° and
180°, we will defer this into another lesson.
The scalar or dot product of the vectors
(x1, y1, z1) and
(x2, y2, z2) is the
scalar quantity:
x1•x2+
y1•y2+
z1•z2.
The vector or cross product of two vectors
is a more complicated entity which we will leave for a later lesson.
Modern physics and mathematics is firmly based on the
algebra of vector spaces.
 The use of lower case letters a, b, and c for the
sides of a triangle is a common convention dating back to Euler
which we will adhere to.
a refers either to the set of points composing the side or the
length of the side, depending on context. The angle opposite side a
is A, the angle opposite side b is B, and the angle
opposite side c is C. If it is a right triangle,
C will be right so c will be the [length of the] hypotenuse.
Given the right triangle ABC with height h (CD) to
the hypotenuse, h=
The use of lower case letters a, b, and c for the
sides of a triangle is a common convention dating back to Euler
which we will adhere to.
a refers either to the set of points composing the side or the
length of the side, depending on context. The angle opposite side a
is A, the angle opposite side b is B, and the angle
opposite side c is C. If it is a right triangle,
C will be right so c will be the [length of the] hypotenuse.
Given the right triangle ABC with height h (CD) to
the hypotenuse, h=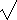 (xy),
whereas a=
(xy),
whereas a=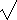 (cx),
and b=
(cx),
and b=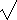 (cy).
Here x+y=c (BD + AD = AB),
and y is the leg of a similar triangle with hypotenuse b,
and x is the leg of a similar triangle with hypotenuse a.
(cy).
Here x+y=c (BD + AD = AB),
and y is the leg of a similar triangle with hypotenuse b,
and x is the leg of a similar triangle with hypotenuse a.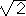 x by the
pythagorean theorem. This ratio of 1/
x by the
pythagorean theorem. This ratio of 1/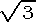 :2.
By the AA Similarity Theorem, any triangle with these angles has these
exact side length ratios.
:2.
By the AA Similarity Theorem, any triangle with these angles has these
exact side length ratios. /36
/36