Back to The Table of Contents
Numbers and Their Application - Lesson 19?
Quadratic Relations and Conic Sections
Lesson Overview
![[parabola, circle, ellipse, and hyperbola as conic sections]](conicsl.jpg) Conic sections arise from the study of the intersection between
a plane and a cone, specifically a double-napped cone.
By double-napped we refer to the fact that the standard
cone studied in geometry with a base and a vertex is only single-napped.
All the surface rays which terminate at the vertex should be extended
to generate the cone envisioned when studying conic sections.
Thus it is more like an hourglass than a jet's nose cone.
The four basic conic sections: circle, ellipse,
parabola, and hyperbola
are detailed below. To obtain these conic sections the intersecting
plane must not pass through the vertex of the cone.
If the plane does pass through the vertex, various degenerate
conic sections result, specifically: a point, a line,
or two intersecting lines.
Conic sections are also known as quadratic relations because the
equations which describe them are second order and not always functions.
These conic sections are excellent mathematical models of the paths taken by
planets, meteors, spacecrafts, light rays, and many other objects.
A third approach defines conics as the locus (collection)
of points satisfying certain geometric properties (distance from
points or lines).
Conic sections arise from the study of the intersection between
a plane and a cone, specifically a double-napped cone.
By double-napped we refer to the fact that the standard
cone studied in geometry with a base and a vertex is only single-napped.
All the surface rays which terminate at the vertex should be extended
to generate the cone envisioned when studying conic sections.
Thus it is more like an hourglass than a jet's nose cone.
The four basic conic sections: circle, ellipse,
parabola, and hyperbola
are detailed below. To obtain these conic sections the intersecting
plane must not pass through the vertex of the cone.
If the plane does pass through the vertex, various degenerate
conic sections result, specifically: a point, a line,
or two intersecting lines.
Conic sections are also known as quadratic relations because the
equations which describe them are second order and not always functions.
These conic sections are excellent mathematical models of the paths taken by
planets, meteors, spacecrafts, light rays, and many other objects.
A third approach defines conics as the locus (collection)
of points satisfying certain geometric properties (distance from
points or lines).
To differentiate between quadratic relations and quadratic
functions, the general equation of a quadratic function follows:
y = ax2 + bx + c.
The above formula, is in the shape of a parabola.
We might want to check to see if it passes the vertical line test
and actually is a function. To perform such a test, simply pick a
value of "x" and draw a vertical line through it. If any such line
crosses the graph more than once then the vertical line test is said to
have failed and the relation is not a function.
Since all polynomials are functions, and this is a polynomial,
we expect it to pass the vertical line test.
Consider next the relation:
y2 = x
Naïvely one might rewrite this as:
y = ![[square root of]](sqrt.gif) (x).
However, we lost one branch and properly it would be written:
y = ±
(x).
However, we lost one branch and properly it would be written:
y = ±![[square root of]](sqrt.gif) (x),
then it would be a parabola opening in the x direction.
But it does not pass the vertical line test and this is only a
relation and not a function.
(x),
then it would be a parabola opening in the x direction.
But it does not pass the vertical line test and this is only a
relation and not a function.
Keeping this in mind, we can now view a quadratic relation, which is
specified by the general equation (or inequality) of the form:
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
(The letters A-F are constants and the "=" sign could also be replaced
with an inequality sign.)
This general equation can be transformed into different
specific equations with the form of that equation
dictated by the actual type of quadratic relation.
A quick review of some essential background information may be useful
at this point.
Distance Formula:
The distance formula is derived from the pythagorean theorem which
says that the sum of the squares of the two sides of right triangle
is equal to the square of the hypotenuse.
Thus the distance (d) between two known points,
(x1,y1) and (x2,y2) is the square root of the following:
d2 = (x2 - x1)2 + (y2 - y1)2.
This relationship will often be used to find the various radii involved.
Completing the Square:
If the coefficient of the quadratic term is equal to one, as in x2+bx,
then the number that will complete the square can be found by halving the linear coefficient,
(b), squaring it, and adding the result:
x2 + bx + (b/2)2=(x + b/2)2.
When the coefficient of the quadratic term is not equal to one you must
factor if out first as illustrated in some examples below.
Vertex:
In a parabola, the x coordinate of the vertex is given by: h = -(b/2a).
The y coordinate is given by k=y(h) or
k=c-b2/(4a).
The x coordinate equation should be easy to remember since the roots (zeroes, x-intercepts,
solutions) of a quadratic are symmetric about the vertex and these roots
are given by the quadratic formula. h = -(b/2a) is thus the portion
of the quadratic formula without the ± portion.
The y coordinate formula can be derived by substituting this h
as x into y(x).
Inequalities:
"<" indicates the region inside the conic section.
">" indicates the region outside the conic section.
|
A circle is a collection of points (x,y) in a coordinate plane,
such that each point is equidistant from a fixed point (h,k)
known as the center. For circles the coefficients for the
x2 and y2 terms in the general
quadratic relationship are equal (i.e. A=C).
|
![[conic section: circle]](circgr.gif)
| ![[+/-sqrt(25-x^2]](circy1.gif)
| ![[-9.4<y<9.4 and -6.2<x<6.2]](circwi.gif)
| | Graph of a circle
| x2 + y2 = 25
| Using a square view window
|
The equation of a circle in standard form is as follows:
(x-h)2 + (y-k)2 = r2
Remember:
- (h,k) is the center point.
- r is the radius from the center to the circle's (x,y) coordinates.
Example:
x2 + y2 + 6x
- 4y - 12 = 0
Step 1 - Commute and associate the x and y terms; additive inverse the -12:
(x2 + 6x) + (y2 - 4y)
= 12
Step 2 - Complete the squares, (what you do to one side be sure to do to the other side):
(x2 + 6x + 9) + (y2 -
4y + 4) = 12 + 9 + 4
Step 3 - Factor:
(x + 3)2 + (y - 2)2 = 25 = 52
Observations
- The conic section will be a circle since the x2 and
y2 terms have the same sign and equal coefficients.
- The center, (h,k), is (-3,2). Note, these are the values
of x and y which make the corresponding term equal to zero.
- The radius of the circle will be 5 units, since the square root
of 25 is 5.
- A circle can be drawn with a compass or one thumbtack and a string.
- The eccentricity of a circle is zero (e=0).
An ellipse is also a collection of points (x,y) in a coordinate plane.
It is very similar to a circle, but somewhat "out of round" or oval.
For an ellipse, the x2 and y2 terms have unequal coefficients,
but the same sign
(A ![[not equal]](ne.gif) C,
and AC > 0).
(The plural of ellipse is ellipses, which is also: ....
Both stem from the same basic root meaning to leave out.) C,
and AC > 0).
(The plural of ellipse is ellipses, which is also: ....
Both stem from the same basic root meaning to leave out.)
|
![[conic section: ellipse]](elipsgr.gif)
|
| ![[y=+/-sqrt(25-2x^2]](elipsy1.gif)
|
| ![[-9.4<y<9.4 and -6.2<x<6.2]](elipswi.gif)
| | Graph of an ellipse
| | 2x2 + y2 = 25
| | Using a square view window
|
Ellipses have the following standard form:
((x-h)/rx)2 +
((y-k)/ry)2 = 1
Remember:
- (h,k) is the center point.
- rx is the length of the radius in the ± x-direction.
- ry is the length of the radius in the ± y-direction.
Example:
x2 + 4y2 = 16
Step 1 - Divide both sides by 16: (x2)/16 +
(4y2)/16 = 1.
Step 2 - Simplify the second term:
(x2)/16 +
(y2)/4 = 1.
Step 3 - Factor/rewrite in standard form:
(x/4)2 + (y/2)2 = 1.
Observations
- The SAME sign but DIFFERENT coefficients for the x2 and
y2 terms tell us that the graph will be an ellipse.
- The two denominators, 4 and 2, (located in step 3) tell us that the
ellipse's vertices are found 4 units from the center (0,0) in the
± x-direction and two other critical points are located
2 units from the center in the ± y-direction.
- rx=4 is called the x-radius and is the distance
from the center to the ellipse in the x-direction.
- ry=2 is called the y-radius and is the distance
from the center to the ellipse in the y-direction.
- The semi-major axis is the larger of rx and ry, in this case 4.
- The semi-minor axis is the smaller of rx and ry, in this case 2.
- Semi- means half. Thus the major and minor axes are twice the semi-major
and semi-minor axes.
- An ellipse can also be described as the set of points in a plane such that the
sum of each point's distance, d1 + d2,
from two fixed points F1 and F2 is constant.
Thus an ellipse may be drawn using two thumbtacks and a string.
- F1 and F2 are foci, that
is each is a focus. They are located at (h±c,k) or (h,k±c)
- The distance from the center to a focus is the focal radius.
- If a is the semi-major axis and b is the semi-minor axis,
then c is the focal radius, where d1 + d2 = 2a,
and c2=a2-b2.
In this case, c2=16-4=12.
- The eccentricity e of an ellipse is given by the ratio: e=c/a.
Since c < a and both are positive this will be between 0 and 1.
An eccentricity close to zero corresponds to an ellipse shaped like a circle,
whereas an eccentricity close to one corresponds more to a cigar.
- The area of an ellipse is: A=
![[pi]](pi.gif) ab.
The circumference must generally be approximated.
ab.
The circumference must generally be approximated.
- The latus recta of an ellipse are line segments through a focus
with endpoints on the ellipse and perpendicular to the major axis.
Their length is 2b2/a.
|
A Parabola has an equation that contains only one squared term.
If the x2 term is excluded, then the graph will open in an x-direction.
If the y2 term is excluded, then the graph will open in a
y-direction. Only graphs which open in the ±y-direction
are quadratic functions, thus those which open in the ±x-direction
are quadratic relations.
|
![[conic section: parabola
+x]](xparagr.gif)
| ![[y=+/-sqrt(25+x)]](xparay1.gif)
| ![[-50<y<50 and -10<x<10]](xparawi.gif)
| | Graph of a parabola
| x=y2 - 25
| In a distorted view window
|
Parabolic functions have the general equation:
y = ax2 + bx + c
A general parabolic relation has the general quadratic relation
equation located on the opening page, except either A=0 or C=0.
Example:
x = -2y2 +12y -10
Observations
- The conic section will be a parabola because there is only
one squared term, y2.
- Since the x2 term is missing, the graph will open in an
x-direction, specifically the -x since C < 0.
- The y-coordinate of the vertex is found by the formula: k = -b/2a.
So that k = -12/2(-2) = 3.
- The x-coordinate of the vertex is: h = -2(32) + 12(3) - 10 = 8.
- The eccentricity of a parabola is one (e=1).
- A parabola can be described as the set of coplanar points each of which
is the same distance from a fixed focus as it is from a fixed
straight line called the directrix.
- The midpoint between the focus and the directrix is the vertex.
The line passing through the focus and the vertex is the axis of the parabola.
- A focal chord is a line segment passing through the focus
with endpoints on the parabola.
- The latus rectum is the focal chord perpendicular to the
axis of the parabola.
- Another standard form for a parabola is:
(x-h)2=4p(y-k) or
(y-k)2=4p(x-h)
- The focus lies on the axis p units from the vertex: (h,k+p) or (h+p,k).
- The directrix is the line y=k-p or x=h-p
|
An Hyperbola has two symmetric, disconnected branches.
Each branch approaches diagonal asymptotes*. Hyperbolas
can be detected by the opposite signs of the x2
and y2 terms. (AC < 0).
|
*(Asymptotes are lines which a graph gets arbitrarily close
to, but never actually touches as the variable continues to move in the
positive or negative direction.)
![[conic section: hyperbola +/-y]](yhypergr.gif)
| ![[y=+/-sqrt(25+x^2]](yhypery1.gif)
| ![[-20<y<20 and -15<x<15]](yhyperwi.gif)
| | Graph of a hyperbola
| -x2+y2 = 25
| In a distorted view window
|
Hyperbolas have the specific equations:
((x-h)/rx)2 - ((y-k)/ry)2
= 1
OR
-((x-h)/rx)2 + ((y-k)/ry)2 = 1
If the sign before the x2 term is POSITIVE (A > 0),
the hyperbola will open toward the ±x-direction. But if the sign
before the y2 term is POSITIVE (C > 0),
the hyperbola will open toward the ±y-direction.
Remember:
- (h,k) is the center point.
- rx is the distance from the center to the hyperbola's ± x-direction
vertex (or asymptote).
- ry is the distance from the center to the hyperbola's ±
y-direction vertex (or asymptote).
- asymptotes have slopes of ry/rx and -(ry/rx)
- A hyperbola is the set of points in a plane such that for each point
(x,y) on the hyperbola, the difference between its distance from
two fixed foci is a constant.
- The semi-major axis, a, is the larger of rx and ry.
- The semi-minor axis, b is the smaller of rx and ry.
- The transverse axis connects the two vertices.
- The conjugate axis is perpendicular to the transverse axis.
- Thus the transverse axis is twice the semi-major, a= abs(d1 - d2).
- c2=a2+b2.
- The eccentricity e of a hyperbola is given by the ratio: e=c/a.
Since c > a and both are positive this will be greater than 1.
If e is close to one, the hyperbola will be narrow and pointed;
whereas if e is large, the hyperbola will be nearly flat.
Example:
-(x/4)2 + (y/3)2 = 1
Observations
- The conic section will be a hyperbola since the x2 and
y2 terms have different signs.
- The graphs open in the ±y-direction
since the sign before the y-term is positive.
- The asymptotes would have a slope of 3/4 or -(3/4).
Suppose you are told to find a polynomial equation for the
set of coplanar points described as follows:
For each point, its distance from the fixed point (-3,0)
is twice its distance from the fixed point (3,0). Thus:
22((x-3)2+(y-0)2)=(x--3)2+(y-0)2
This comes from applying the distance formula, but both sides have been squared.
This leads to the following relationships:
4(x2-6x+9+y2)=x2+6x+9+y2
3x2-30x+27+3y2=0 or
(x-5)2+y2=42.
We thus have a circle centered at (5,0) with radius 4.
Another example might be as follows:
Each point is equidistant from the point (3,-4) and the line y=2. Thus:
(x-3)2+(y+4)2=(x-x)2+(y-2)2.
x2-6x+9+y2+8y+16=0+y2-4y+4.
x2-6x+12y+21=0 or y+1=-(x-3)2/12.
We thus have a parabola with vertex at (3,-1) opening in the -y direction.
One last example is as follows:
For each point, its distance from the point (0,3) is
3/2 times its distance from the line y=-3.
4((x-0)2+(y-3)2)=9((x-x)2+(y+3)2)
4(x2+y2-6y+9)=9(y2+6y+9)
4x2-5y2-78y-45=0
We thus have a hyperbola opening in the x direction.
Several steps have been omitted from the above derivations and it
behooves the student to check these over, verify, and master them,
because several common algebraic mistakes often occur.
The xy-term, which rotates the graph and its shape, is not discussed
in any of the above equations.
Some information regarding it will be quickly noted here, however.
The discriminant (B2-4AC) is used to determine
which conic section will result.
If the discriminant is less than zero we have a circle (if A = C) or an ellipse;
if the discriminant is equal to zero we have a parabola;
if the discriminant is greater than zero we have a hyperbola.
Our equation can be rewritten with B' = 0 by
rotating the coordinate axes through an angle 0, where
cot(20)=(A-C)/B.
Note that F = F' is invariant under rotation.
Note also A + C = A' + C' and
B2-4AC = (B')2-4A'C'.
We choose B' = 0.
The simplest hyperbola comes from the graph:
y=1/x or xy=1.
For this relationship we note that A=0, B=1, and C=0.
Thus cot 20=0 or 0=![[pi]](pi.gif) /4.
Thus in a x'y' coordinate system, which is rotated by 45° from
our normal xy coordinate system, our equation would be:
/4.
Thus in a x'y' coordinate system, which is rotated by 45° from
our normal xy coordinate system, our equation would be:
(x'/![[square root of two]](sqrt2.gif) )2-
(y'/
)2-
(y'/![[square root of two]](sqrt2.gif) )2=1.
)2=1.
Work on this web page was started in the fall of 1998 with
data entry assistance by Sally Gregg, BCMSC class of 2000.
A major update was done in February 2001.
Ashley shared this link which has some good dynamic graphs:
http://xahlee.org/SpecialPlaneCurves_dir/specialPlaneCurves.html
Mary shared this link which has some free (to students) software:
http://www.romanlab.com/3dg/#info
Activities can be located at:
testing
Apparently the conic section graphics come originally from Foerster
(and may not have been uncopyrighted as a web site claimed some years back).
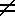 C and AC > 0.)
C and AC > 0.)
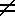 C and AC > 0.)
C and AC > 0.)
![[parabola, circle, ellipse, and hyperbola as conic sections]](conicsl.jpg)
![[conic section: circle]](circgr.gif)
![[+/-sqrt(25-x^2]](circy1.gif)
![[-9.4<y<9.4 and -6.2<x<6.2]](circwi.gif)
![[conic section: ellipse]](elipsgr.gif)
![[y=+/-sqrt(25-2x^2]](elipsy1.gif)
![[-9.4<y<9.4 and -6.2<x<6.2]](elipswi.gif)
![[conic section: parabola
+x]](xparagr.gif)
![[y=+/-sqrt(25+x)]](xparay1.gif)
![[-50<y<50 and -10<x<10]](xparawi.gif)
![[conic section: hyperbola +/-y]](yhypergr.gif)
![[y=+/-sqrt(25+x^2]](yhypery1.gif)
![[-20<y<20 and -15<x<15]](yhyperwi.gif)
![]() /4.
Thus in a x'y' coordinate system, which is rotated by 45° from
our normal xy coordinate system, our equation would be:
/4.
Thus in a x'y' coordinate system, which is rotated by 45° from
our normal xy coordinate system, our equation would be:![]() )2-
(y'/
)2-
(y'/![]() )2=1.
)2=1.