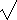(10)),
we apply the t-test and find a P-value
of either 8.73×10-5 or
4.36×10-5 depending on
whether we do a one-tailed or two-tailed test.
In either case our results are
statistically significant at the 0.0001 level.
Our two hypotheses have special names: the null hypothesis represented by H0 and the alternative hypothesis by Ha. Historically, the null (invalid, void, amounting to nothing) hypothesis was what the researcher hoped to reject. These days it is common practice not to associate any special meaning to which hypothesis is which. (But this common practice may not yet have extended into behavioral science. The research hypothesis becomes the alternate hypothesis and the null hypothesis or "straw man" to be knocked down is so determined.) Although simple hypotheses would be easiest to test, it is much more common to have one of each type or perhaps for both to be composite. If the values specified by Ha are all on one side of the value specified by H0, then we have a one-sided test (one-tailed), whereas if the Ha values lie on both sides of H0, then we have a two-sided test (two-tailed). A one-tailed test is sometimes called a directional test and a two-tailed test is sometimes called a nondirectional test.
The outcome of our test regarding the population parameter will be that we either reject the null hypothesis or fail to reject the null hypothesis. It is considered poor form to "accept" the null hypothesis, although if we fail to reject it, that is in fact essentially what we are doing. When we reject the null hypothesis we have only shown that it is highly unlikely to be true---we have not proven it in the mathematical sense. The research hypothesis is supported by rejecting the null hypothesis. The null hypothesis locates the sampling distribution, since it is (usually) the simple hypothesis, testing against one specific value of the population parameter. Establishing the null and alternative hypotheses is sometimes considered the first step in hypothesis testing.
| Reject\Truth | H0 True | Ha True |
|---|---|---|
| Reject Ha | no error | False positive, Type II, beta=P(Reject Ha|Ha true) |
| Reject H0 | False negative, Type I, alpha=P(Reject H0|H0 true) | no error |
The term false positive for type II errors comes from perhaps a blood test where the test results came back positive, but it is not the case (false) that the person has whatever was being tested for. The term false negative for type I errors then would mean that the person does indeed have whatever was being tested for, but the test didn't find it. When testing for pregnancy, AIDS, or other medical conditions, both types of errors can be a very serious matter. Formally, alpha=P(Accept Ha|H0 true), meaning the probability that we "accepted" Ha when in fact H0 was true. Alpha is the term used to express the level of significance we will accept. For 95% confidence, alpha=0.05. For 99% confidence, alpha=0.01. These two alpha values are the ones most frequently used. If our P-value, the high unlikeliness of the H0, is less than alpha, we can reject the null hypothesis. Alpha and beta usually cannot both be minimized---there is a trade-off between the two. Ideally, of course, we would minimize both. Historically, a fixed level of significance was selected (alpha=0.05 for the social sciences and alpha=0.01 or alpha=0.001 for the natural sciences, for instance). This was due to the fact that the null hypothesis was considered the "current theory" and the size of Type I errors was much more important than that of Type II errors. Now both are usually considered together when determining an adequately sized sample. Instead of testing against a fixed level of alpha, now the P-value is often reported. Obviously, the smaller the P-value, the stronger the evidence (higher significance, smaller alpha) provided by the data is against H0.
Example: On July 14, 2005 we took 10 samples
of 20 pennies set on edge and the table banged.
The resultant mean of heads was 14.5 with a standard deviation of 2.12.
Since this is a small sample, and the population variance is unknown,
after we calculate a t value
and obtain t=6.71=(14.5-10)/(2.12/
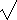(10)),
we apply the t-test and find a P-value
of either 8.73×10-5 or
4.36×10-5 depending on
whether we do a one-tailed or two-tailed test.
In either case our results are
statistically significant at the 0.0001 level.
|
The P-value of a test is the probability that the test
statistic would take a value as extreme or more extreme than that actually observed, assuming H0 is true. |
Setting the level of significance will correspond to the probability that we are willing to be wrong in our conclusion if a type I error was committed. That probability will correspond to certain area(s) under the curve of a probability distribution. Those areas, known as the region of rejection is bounded by a critical value or critical values which are often computed. Alternatively, one might compare the test statistic with the corresponding point(s) on the probability curve. These are equivalent ways of viewing the problem, just different units of measure are being used. In a one-tailed test there is one area bounded by one critical value and in a two-tailed test there are two areas bounded by two critical values. Which tail (left or right) under consideration for a one-tailed test depends on the direction of the hypothesis.
Establishing the significance level and the corresponding critical value(s) is sometimes considered the second step in hypothesis testing. Presumeably we have determined how the statistic we wish to test is distributed. This sampling distribution is the underlying distribution of the statistic and determines which statistical test will be performed.
![[sigma]](../webtexts/sigma.gif){kind=small}
).
Realistically,
is unknown. Often a preliminary sample will be conducted so that a
reasonable estimate of this critical population parameter can be made.
If such a preliminary sample is not made,
but confidence intervals for the population mean are
to be constructing using an unknown
, then the
distribution known as the Student t distribution can be used.Testing a hypothesis at the alpha=0.05 level or establishing a 95% confidence interval are again essentially the same thing. In both cases the critical values and the region of rejection are the same. However, we will more formally develop the confidence intervals in lesson 9 (Hinkle chapter 9).
First, a little history about this distribution's curious name. William Gosset (1876-1937) was a Guinness Brewery chemist who needed a distribution that could be used with small samples. Since the Irish brewery did not allow publication of research results, he published in 1908 under the pseudonym of Student. We know that large samples approach a normal distribution. What Gosset showed was that small samples taken from an essentially normal population have a distribution characterized by the sample size. The population does not have to be exactly normal, only unimodal and basically symmetric. This is often characterized as heap-shaped or mound shaped.
Following are the important properties of the Student t distribution.
2=1
for the standard normal distribution).
To use the Student t distribution which is often referred to just as the t distribution, the first step is to calculate a t-score. This is much like finding the z-score. The formula is:
t = (![[x bar]](../webtexts/xbar.gif){kind=small} - µ) ÷
(s/sqrt(n))
|
Actually, since the population mean is likely also unknown, the sample mean must be used. The critical t-score can be looked up based on the level of confidence desired and the degrees of freedom. Degrees of freedom is a fairly technical term which permeates all of inferential statistics. It is usually abbreviated df. In this case, it is the very common value n-1.
|
In general, the degrees of freedom is the number of values that
can vary after certain restrictions have been imposed on all values. |
Where does the term degrees of freedom come from? Suppose, for example, that you have a phone bill from Ameritech that says your household owes $100. Your mother and father state that $70 of it is theirs and that your younger sibling owes only $5. How much does that leave you? Here, n=3 (parents, sibling, you), but once you have the total (or mean) and two more pieces of information, the last data element is constrained. The same is true with the degrees of freedom, you can arbitrarily use any n-1 data points, but the last one will be determined for a given mean. Another example is with 10 tests that averaged 55, if you assign nine people random grades, the last test score is not random, but constrained by the overall mean. Thus for 10 tests and a mean, there are nine degrees of freedom.
If the interval calls for a 90% confidence level, then alpha = 0.10 and alpha/2 = 0.05 (for a two-tailed test). Tables of t values typically have a column for degrees of freedom and then columns of t values corresponding with various tail areas. An abbreviated table is given below. For a complete set of values consult a larger table or your TI-83+ graphing calculator. DISTR 5 gives tcdf. tcdf expects three arguments, lower t value, upper t value, and degrees of freedom. Since no inverse t function is given on the calculator, some guessing may be involved. Note how tcdf(9.9,9E99,2) indicates a t value of about 9.9 for a one tailed area of 0.005 with two degrees of freedom. Please locate the corresponding value of 9.925 in the table.
As with other confidence intervals, we use the t-score to obtain the margin of error term which is added and subtracted from the statistic of interest (in this case, the sample mean) to obtain a confidence interval for the parameter of interest (in this case, the population mean). In this case the margin of error is defined (since you don't have population standard deviation you use the sample's) as:
| ME = talpha/2 • (s ÷ sqrt(n)) |
Your confidence interval should look like:
- ME < µ <
+ ME.
| Degrees of Freedom\1/2 tails | .005/.01 | .01/.02 | .025/.05 | .05/.10 | .10/.20 |
|---|---|---|---|---|---|
| 1 | 63.66 | 31.82 | 12.71 | 6.314 | 3.078 |
| 2 | 9.925 | 6.965 | 4.303 | 2.920 | 1.886 |
| 3 | 5.841 | 4.541 | 3.182 | 2.353 | 1.638 |
| 4 | 4.604 | 3.747 | 2.776 | 2.132 | 1.533 |
| 5 | 4.032 | 3.365 | 2.571 | 2.015 | 1.476 |
| 10 | 3.169 | 2.764 | 2.228 | 1.812 | 1.372 |
| 15 | 2.947 | 2.602 | 2.132 | 1.753 | 1.341 |
| 20 | 2.845 | 2.528 | 2.086 | 1.725 | 1.325 |
| 25 | 2.787 | 2.485 | 2.060 | 1.708 | 1.316 |
| z | 2.576 | 2.326 | 1.960 | 1.645 | 1.282 |
Although the t procedure is fairly robust, that is it does not change very much when the assumptions of the procedure are violated, you should always plot the data to check for skewness and outliers before using it on small samples. Here small can be interpreted as n < 15. If your sample is small and the data is clearly nonnormal or outliers are present, do not use the t. If your sample is not small, but n < 40, and there are outliners or strong skewness, do not use the t. Since the assumption that the samples are random is more important that the normality of the population distribution, the t statistic can be safely used even when the sample indicates the population is clearly skewed, if n > 40.
The two sample t tests will be discussed in lesson 10.
Statistical precision can be defined as the reciprocal of the standard error for a given test statistic. Statistical precision is thus influenced directly by sample size, or rather its square root. Critics have called inferential statistics a "numbers game" in that with a large enough sample we should be able to prove most anything. This, however, ignores the careful design and other work done during the investigation which should give practical considerations to the statistical implications. Once the tools of inferential statistics helps one analyze data, these results still need a knowledgeable interpretation.
| BACK | HOMEWORK | ACTIVITY | CONTINUE |
|---|