Back to the Table of Contents

Applied Statistics - Lesson 15

More Parametrics--Ordinal

Lesson Overview

The chi-square statistic is used when the dependent variable is at the nominal level and our parametric assumptions of normality and homogeneity of variance cannot be met as discussed in the previous lesson. In this lesson we explore nonparametric tests of significance for ordinal dependent variables.

One Sample Tests

Three common one sample tests of signficance are: 1) the one-sample sign test; 2) the Mann-Kendall test for trends; and 3) the Kolmogorov-Smirnov one-sample test. (Links or more information will be added as time permits.)

Two Sample Tests

We explore here two common tests of significance for the two sample case when the dependent variable is measured at the ordinal level. First, the median test tests the hypothesis that two samples have been selected from populations with equal medians. One starts by finding this common median by ordering the scores from both groups together and then determining the median. Then a 2×2 contingency table is formed with the frequency counts of how many from each group are above or below the common median. A chi-square statistic is generated using the simplified formula:
2 = n(AD - BC)2/ ((A+B)(C+D)(A+C)(B+D))
and compared with a critical value in the normal way.

Second, the statistically more powerful Mann-Whitney U test, tests not only the median, but also the total distribution (central tendancy and distribution). The null hypothesis specifies that there is no difference in the scores of the two populations sampled. Two U values are calculated and the smaller one is selected for checking in a table of critical values. The null hypothesis is reject if the computed U is less than the table value. The U values take into account the number of data elements in each sample (n1 and n2) and the sum of the ranks in each group (R1 and R2). Calculate Ui = n1n2 + ½ni(ni + 1) - Ri for both i=1 and i=2.

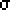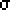When both groups are larger than 20, the sampling distribution approaches the normal distribution and a z-score can be computed from the sampling distribution mean µU = ½n1n2, and standard deviation U = sqrt( n1n2 (n1 + n2 +1)/12). The z score is calculated in the usual way with z = (U - µU)/ U.

A table of Mann-Whitney critcal U values is given below for alpha=0.05 (1-tailed=directional Ha) and selected sample sizes only. More extensive tables are readily available.

ni\nj23456789101520
2 0 0 0 1 1 1 2 2 2 4 5
3 0 1 1 2 3 3 4 5 5 8 12
4 0 1 2 3 4 5 6 7 8 13 19
5 1 2 3 5 6 7 9 10 12 19 26
6 1 3 4 6 8 9 11 13 15 24 33
7 1 3 5 7 9 12 14 16 18 29 40
8 2 4 6 9 11 14 16 19 21 34 48
9 2 5 7 10 13 16 19 22 25 40 55
10 2 5 8 12 15 18 21 25 28 45 63
15 4 8 13 19 24 29 34 40 45 73 101
20 5 12 19 26 33 40 48 55 63 101 139

K-Sample Tests

The test statistics H for the Kruskal-Wallis one-way analysis of variance is calculated in a similar manner to the Mann-Whitney U. The null hypothesis is that there is no difference in the distribution of data in the K populations. The alternate hypothesis would be that at least two of the K populations or a combination of populations differ. Although we won't give the formula here, the sampling distribution is the chi-square with K - 1 degrees of freedom.

Tied ranks generally have minimal effect on both the Mann-Whitney U and Kruskal-Wallis H and a correction factor can be applied. However, results from either test might be questionable when there are an excessive number of tied ranks.

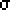Two Sample Tests, Dependent (matched)

The Wilcoxon matched-pairs signed-rank test was developed for use with dependent samples and ordinal data. The null hypothesis is again stated in general terms of no difference between populations. The test statistic, termed T, is formed by ranking the pre-/post-test differences but including a sign (negative for larger post-test score). The ranks with the least frequent sign are summed and the resulting statistic compared with a table of critical values. With samples larger than 25 the sampling distribution approaches the normal distribution with µT=¼n(n + 1) and standard deviation T = sqrt( n(n + 1)(2n + 1)/24). The z score is calculated in the usual way with z = (T - µ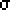T)/ T.

In conclusion we wish to emphasize both the role of nonnormal populations and small sample size in the use of these statistics. Larger samples give better statistical precision, but sometimes a limited population or expense preclude obtaining such. Thus the best statistical test for a given situation is defined more in terms of the research conditions than in terms of parametric vs nonparametric.

BACK NO HOMEWORK! ACTIVITY THE END