Back to the Table of Contents
A Review of Basic Geometry - Lesson 1
Undefined: Points, Lines, and Planes
Lesson Overview
In Discrete Geometry, a point is a dot. Lines are composed
of an infinite set of dots in a row. Dots may or may not have size and shape, depending
on the version studied. Some common applications of discrete geometry include
computer displays and printers. The computer screen I am working on at the
moment has 80 columns and 25 rows of characters. Each character is composed
of dots in an array about 12 wide and 30 high. In total, an array of
1024 by 768 individual pixels is utilized. When printed, a laser printer with
600 dots per inch is being used. At 6 lines per vertical inch and 10
characters per horizontal inch, each character is appropriately spaced
in its own array of 60 by 100 pixels. Early laser printers were 300 dpi.
This and lower resolution modes are usually available to reduce the
volume of data needed for a full page of graphics.
A recent development was Resolution Enhancement technology
which allowed them to vary the dot size on laser printers,
thus smoothing the edges of curves.
Dot matrix printers are similar, but have bigger dots and print them
a few at a time.
Also, our TI-84+ calculators utilize a screen of 95 by 63 pixels.
These, in turn, are used for 16 characters wide by 8 characters high, so
each character has an 8 by 8 grid, but space must be allowed between them.
(The first number should be the horizontal quantity and the second number
the vertical quantity, just like an (x,y) ordered pair.)
Oblique lines will often look like steps due to this discrete nature.
Other examples of discrete geometry include some paintings, signs made of
individual light bulbs, and marching bands. Lines are either
horizontal, vertical, or oblique. Discrete lines
go on forever, so only a portion is ever displayed. Discrete lines
cross each other either with or without a point in common.
The ancient Greeks idealized points as an exact location,
having no size or shape. A line is then the set of points extending
in both directions and containing the shortest path between any two points
on it. The technical term for shortest path is geodesic.
There is then exactly one line containing any two points.
The number line is a common example, with
each point given a coordinate. Such lines are said to be
coordinatized. Number lines are dense
like the rationals.
This means that between any two points is another point.
They are also continuous like the reals—there are no gaps.
Once points are coordinatized, distances can be measured.
The Cartesian Coordinate System was invented by
Pierre de Fermat and René Descartes about 1630.
Cartesius was the name Descartes used for himself in his
writings which were in Latin.
Each point in the plane
is now a location in the Cartesian plane
and is represented by an ordered pair.
The first ordinate is usually termed x and
the second ordinate y.
The coordinate system has an origin where the
x-axis and y-axis intersect.
A line is now a set of ordered pairs such that Ax + By = C.
This standard form, integer constant form or
Ax + By = C form complements the y=mx+b
form you already should know. Converting between them should be routine.
Related properties such as slope
were already studied in numbers lesson 12.
A fourth description of point is of a node or vertex in a network.
A line is now an arc connecting either two different nodes
or one node to itself.
This description is utilized in Graph Theory.
Historically, the field of topology,
often called rubber-sheet geometry,
was invented by Euler to solve the Königsberg Bridge Problem in 1736.
Networks are either traversable or not,
depending on the number of odd nodes.
A node is odd if the number of arcs to it is odd, else it is even.
The network for the Königsberg Bridge Problem had four odd nodes.
Since four is more than two, it is not traversable—since you
must either start or finish at an odd node.
Hence, the residents could not walk over
all the bridges without retracing their steps.
Networks commonly appear as telephone or other communication networks,
power grids, or even highway systems.
A favorite of mathematicians is the
network
of papers published by joint authors. At its center is Paul Erdös.
This network has been well studied and has a known "diameter" of 23.
Although previously thought to be single digit, when the paper
based on my dissertation work is published, I should have a computable
approximation for my Erdös number of about 6.
Graph theory has other appliciations such as wire-wrapping
old computer circuits, or laying out complex chip designs.
The words points, lines, and planes are
left undefined,
or rather defined by usage in most geometries.
We thus avoid circularity: where definitions circle back
to one previously defined. This tradition was only started about
100 years ago by David Hilbert.
However, we can form definitions using our undefined terms.
|
A figure is a set of points.
|
|
Space is the set of all points.
|
|
Three or more points are collinear
if and only if they are on the same line.
|
|
Four or more points are coplanar
if and only if they are in the same plane.
|
When all points in space are collinear, the geometry is one-dimensional.
When all points in space are coplanar, the geometry is two-dimensional
(2D) or plane geometry. Common figures we will study, such as squares,
circles, and triangles are two-dimensional.
Other figures, such as spheres, boxes, cones, and other tangible objects do
not lie in one plane and are three-dimensional or 3D.
The study of these is called solid geometry.
What our undefined terms really mean depends on which set of
axioms or postulates we choose.
Historically, axioms were self-evident truths,
hence the word postulate, meaning assumption is now more commonly used.
The postulates we will use correspond with Euclidean Geometry
and fit both the synthetic and coordinate geometries introduced above,
but not discrete geometry nor graph theory.
Euclidean Geometry is so named because is was well established in the
set of thirteen books called Elements written by
Euclid about
300 B.C. These books also
dealt with other areas of mathematics. It is widely believed that
Euclid summarized much of the known mathematics of his time.
His geometry starts with five assumptions (requests),
the fifth becoming very controversial by the early 1800's.
Several online
versions
exist, including a wonderful color
version
from the early 1800's.
Note, in Elements, point, line (segment), straight line (line)
are all defined terms. Several of Euclid's common notions
are the same as our algebraic properties given
in numbers or in the
next lesson.
Specifically, the following properties are needed:
transitive, addition (subtraction) property
of equality, and the equality to inequality property.
Euclid's five requests are:
- To draw a straight line from any point to any point.
- To produce a finite straight line continuously in a straight line.
- To describe a circle with any center and distance.
- That all right angles are equal to one another.
- That, if a straight line falling on two straight lines
make the interior angles on the same side less than two right angles,
the two straight lines, if produced indefinitely, meet on that side on
which are the angles less than the two right angles.
Compare the wording given here for Euclid's fifth postulate with that
given below.
Euclid's Fifth Postulate:
Through a point not on a line, one and only one line can be drawn
parallel to that line.
|
Rejecting Euclid's Fifth Postulate leads one to Non-euclidean Geometries.
A substantial portion of standard geometry can be developed without
it and is termed Neutral Geometry.
Adapting variations of Euclid's Fifth Postulate leads to several types
of Geometries involving positively or negatively curved surfaces.
A plane or cylinder has zero curvature.
A sphere has positive curvature.
A saddle has negative curvature.
On a sphere no line parallel can be drawn through a point outside a line.
On a saddle, more than one such parallel line can be drawn.
The geometry of a saddle shaped surface is known as hyperbolic geometry
(from the Greek to exceed).
The geometry of a sphere required additional changes to the usual
axioms because betweenness is no longer meaningful and must be replaced
with separation. This is known as Elliptic Geometry.
The last geometry we will discuss is Reimannian Geometry.
Its full development requires calculus, which is beyond the scope of
these lessons. This geometry was popularized by Albert Einstein
when he developed his theory of General Relativity with the
notion that space is curved by the presence of mass.
Euclid is known as the father of geometry.
When Ptolomy asked if there was an easier way to learn geometry
Euclid replied: "There is no royal road to Geometry."
There are other geometry between incidence and the coordinatized
Euclidean version with least upper bound. Just ask the author
sometime and he might show you the book he is typing....
All in all, it takes hundreds of pages to cover the ground
covered by the point-line-plane postulate given below!
One geometry not cover there (yet) is projective geometry
which has an important dualism between points and lines.
Compare the following: 2 points determine a line; and 2 lines determine a point.
We will start with three assumptions known collectively as the
Point-Line-Plane Postulate.
- Unique Line Assumption
Through any two points is exactly one line.
- Number Line Assumption
Every line is a set of points which can be put into
a one-to-one correspondence with the real numbers.
Any point can correspond with 0 (zero) and any
other point can correspond with 1 (one).
- Dimension Assumption
Given a line in a plane, there exists at least one point in the plane
that is not on the line.
Given a plane in space, there exists at least one point in space
that is not in the plane.
|
The first assumption is sometimes stated simply as:
two points determine a line.
It should be clear that the Unique Line Assumption does not apply to lines in
discrete geometry (part of different lines near each other) or
graph theory (more than one arc connecting two nodes).
The Number Line Assumption also does not apply to lines in graph theory
since it guarantees infinitely many points.
These postulates herd us quickly down the road toward the development
of Euclidean geometry. Many interesting geometries could be investigated if
we started with much simpler postulates. The number line assumption
in particular immediately gives us measurement, distance, betweenness, and
infinite points.
We can now prove our first theorem by
using the Unique Line Assumption. (See book for details.)
|
Theorem: Two different lines intersect in at most one point.
|
Two coplanar lines m and n are
parallel, written m||n,
if and only if they have no points in common (or they are identical).
|
Note: this definition of parallel is typical for our textbook
but is often at odds with what students are taught in middle school.
It is an example of an inclusive definition.
Along a similar vein, a quadrilateral which happens to be square
is still a rectangle. An equilateral triangle is still isosceles.
A square is still a trapezoid. Teresa Heinz-Kerry is still a Heinz.
Although standardized tests and contests tend to avoid these ambiguities,
one must be on the lookout for such problems!
Warning our geometry textbook only motivates betweenness using
numbers on a number line.
It neither defines it nor adopts an axiom to develop it.
|
Below are four typical axioms of betweenness.
A*B*C means point B is between point A and point C.
- If A*B*C, then A, B, and C are three distinct
points all lying on the same line, and C*B*A.
- Given any two distinct points A and B,
there exist points C, D, and E lying on
![[line AB]](line2ab.gif) such that
C*A*B, A*D*B, and A*B*E. such that
C*A*B, A*D*B, and A*B*E.
- If A, B, and C are three distinct points
lying on the same line, then one and only one of the points
is between the other two.
- If Q and R are on opposite sides of line L, then line QR intersects L.
|
The segment (or line segment) with endpoints
A and B, denoted
![[segment AB]](seg1ab.gif) ,
is the set consisting of the distinct points A and B
and all points between A and B. ,
is the set consisting of the distinct points A and B
and all points between A and B.
|
The ray with endpoint A and containing a second point B,
denoted ![[ray AB]](rayab1.gif) ,
consists of the points on ,
consists of the points on
![[segment AB]](seg1ab.gif) and all points for which B is between each of them and A.
and all points for which B is between each of them and A.
|
![[ray AB]](rayab1.gif) and and
![[ray AC]](rayac1.gif) are opposite rays
if and only if A is between B and C. are opposite rays
if and only if A is between B and C.
|
Please note that our segments and rays are closed—they include
their endpoints. In other geometries, segments and rays could be
open (or half open) and exclude their endpoint(s). Ultimately, another axiom, the
least upper bound axiom is needed to deal with this.
Three more important assumptions are known as the Distance Postulate.
- Uniqueness Property
On a line, there is a unique distance between two points.
- Distance Formula
If two points on a line have coordinates x and y,
the distance between them is |x - y|.
- Additive Property
If C is on ![[segment AB]](seg1ab.gif) ,
then AC + CB = AB. ,
then AC + CB = AB.
|
Distances are positive values and the symbol for absolute value:
|-10| = 10 is utilized above. The distance between two points
A and B is written AB.
You cannot multiply points,
so AB always represents the distance between, and never their product.
Because distance is always positive, AB = BA.
The term directed distance is sometimes uses to convey not only
magnitude, but also the direction.
It is thus a vector instead of a scalar quantity.
Please note carefully the differences among
distance AB, segment
![[segment AB]](seg1ab.gif) , ray , ray
![[ray AB]](rayab1.gif) , and line , and line
![[line AB]](line2ab.gif) , ,
|
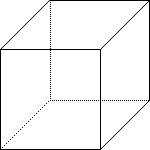 Although mathematicians don't often draw in perspective,
the concept and terminology are important.
A perspective drawing gives a two-dimensional object
a feeling of depth. Parallel lines now meet in the distance
at a vanishing point. Often one thinks of the
artist's or observer's eye as this vanishing point and sketches
lines of sight to connect them.
Objects can be drawn in one- two- or three-point perspective,
depending on how many vanishing points are used.
Parallel horizontal and vertical lines go to their own vanishing point,
depending on their relationship to each other.
Multiple vanishing points should line up on the vanishing line
which corresponds with the horizon line at
the height of the observer's eye.
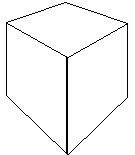
Mathematicians typically draw non-perspective drawings,
utilizing dashed or dotted hidden lines to indicate
parts not normally seen. Compare the two pictures shown
above left and below. Find the vanishing points for the
drawing below.
Although mathematicians don't often draw in perspective,
the concept and terminology are important.
A perspective drawing gives a two-dimensional object
a feeling of depth. Parallel lines now meet in the distance
at a vanishing point. Often one thinks of the
artist's or observer's eye as this vanishing point and sketches
lines of sight to connect them.
Objects can be drawn in one- two- or three-point perspective,
depending on how many vanishing points are used.
Parallel horizontal and vertical lines go to their own vanishing point,
depending on their relationship to each other.
Multiple vanishing points should line up on the vanishing line
which corresponds with the horizon line at
the height of the observer's eye.
Mathematicians typically draw non-perspective drawings,
utilizing dashed or dotted hidden lines to indicate
parts not normally seen. Compare the two pictures shown
above left and below. Find the vanishing points for the
drawing below.
![[line AB]](line2ab.gif) such that
C*A*B, A*D*B, and A*B*E.
such that
C*A*B, A*D*B, and A*B*E.
![[segment AB]](seg1ab.gif) ,
is the set consisting of the distinct points A and B
and all points between A and B.
,
is the set consisting of the distinct points A and B
and all points between A and B.
![[ray AB]](rayab1.gif) ,
consists of the points on
,
consists of the points on
![[ray AC]](rayac1.gif) are opposite rays
if and only if A is between B and C.
are opposite rays
if and only if A is between B and C.
 Although mathematicians don't often draw in perspective,
the concept and terminology are important.
A perspective drawing gives a two-dimensional object
a feeling of depth. Parallel lines now meet in the distance
at a vanishing point. Often one thinks of the
artist's or observer's eye as this vanishing point and sketches
lines of sight to connect them.
Objects can be drawn in one- two- or three-point perspective,
depending on how many vanishing points are used.
Parallel horizontal and vertical lines go to their own vanishing point,
depending on their relationship to each other.
Multiple vanishing points should line up on the vanishing line
which corresponds with the horizon line at
the height of the observer's eye.
Mathematicians typically draw non-perspective drawings,
utilizing dashed or dotted hidden lines to indicate
parts not normally seen. Compare the two pictures shown
above left and below. Find the vanishing points for the
drawing below.
Although mathematicians don't often draw in perspective,
the concept and terminology are important.
A perspective drawing gives a two-dimensional object
a feeling of depth. Parallel lines now meet in the distance
at a vanishing point. Often one thinks of the
artist's or observer's eye as this vanishing point and sketches
lines of sight to connect them.
Objects can be drawn in one- two- or three-point perspective,
depending on how many vanishing points are used.
Parallel horizontal and vertical lines go to their own vanishing point,
depending on their relationship to each other.
Multiple vanishing points should line up on the vanishing line
which corresponds with the horizon line at
the height of the observer's eye.
Mathematicians typically draw non-perspective drawings,
utilizing dashed or dotted hidden lines to indicate
parts not normally seen. Compare the two pictures shown
above left and below. Find the vanishing points for the
drawing below.