![[pi]](pi.gif) r2.
Analogous to the unit circle is the unit sphere.
Similarly, just as there are 2
r2.
Analogous to the unit circle is the unit sphere.
Similarly, just as there are 2![[pi]](pi.gif) radians
of angle in one revolution,
there are 4
radians
of angle in one revolution,
there are 4![[pi]](pi.gif) steradians of solid angle
in all directions.
steradians of solid angle
in all directions.
| Lateral Area of a prism: perimeter × height |
| Lateral Area of a cylinder: circumference × height. |
| Lateral Area of a regular pyramid: ½ perimeter × slant height. |
| Lateral Area of a right cone: ½ perimeter × slant height. |
The lateral area of a regular pyramid or right cone is similar to that of prisms, but since each face is a triangle (or triangle-like), there is a factor of one half. The lateral area is thus half the slant height times the perimeter. The slant height is the distance from the vertex to the edge of the base where it is halfway between the base's vertices. If the pyramid is irregular and certainly if the cone is oblique, the surface area might not be calculatable using elementary techniques (which is a fancy way to say you may need calculus). It depends on if you can obtain the altitude (slant height) of each triangular face.
| Surface Area = Lateral Area + n × Bases n = 2 for prisms/cylinders; n = 1 for pyramids/cones; n = 0 for spheres. |
The surface area of a pyramid or cone is the lateral area plus the area of the single base.
The surface area of a sphere is equal to 4![[pi]](pi.gif) r2.
Analogous to the unit circle is the unit sphere.
Similarly, just as there are 2
r2.
Analogous to the unit circle is the unit sphere.
Similarly, just as there are 2![[pi]](pi.gif) radians
of angle in one revolution,
there are 4
radians
of angle in one revolution,
there are 4![[pi]](pi.gif) steradians of solid angle
in all directions.
steradians of solid angle
in all directions.
Example: Consider a right pyramid A-BCDE with vertex A and square base BCDE of length 20" on each side and a slant height of 26". What are its lateral and surface areas?
Answer: We don't need the height for this calculation, but we will calculate it anyway to stress the difference between slant height and height. The slant height is the hypotenuse of a right triangle where the height is one leg and 20"/2 = 10" is the other leg. Thus 102 + h2 = 262 or 100 + h2 = 676. Thus h2 = 576 or h = 24". The lateral surfaces are all triangles with a base of 20" and a height (the slant height) of 26". There are four of them. Thus the lateral area is 4×½×20"×26" = 1040 in2. The base is 20" square or 400 in2. Thus the [total] surface area is 1440 in2.
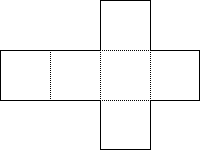
 Understanding surface area may be clearer if you refer back to the net
associated with the object.
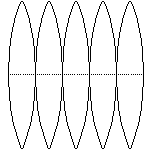
At left is a net for a cube and at right a portion of a net for a sphere.
Each of these portions of a sphere is called a gore.
Understanding surface area may be clearer if you refer back to the net
associated with the object.
At left is a net for a cube and at right a portion of a net for a sphere.
Each of these portions of a sphere is called a gore.
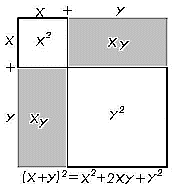 Now is a good time to review something learned in algebra, namely
(x + y)2 =
x2 + xy + xy + y2 =
x2 + 2xy + y2.
The diagram at the right should clarify this further,
help you remember the FOIL method,
as well as give a physical basis for this relationship.
(Remember also, the square root of (x2 + y2)
does NOT equal x + y.)
Consider extending the FOIL method first into trinomials:
(a + b + c)(d + e + f)
= ad + ae + af + bd + be +
bf + cd + ce + cf.
The distributive property is another way to consider this situation.
Here the box method is useful.
Now is a good time to review something learned in algebra, namely
(x + y)2 =
x2 + xy + xy + y2 =
x2 + 2xy + y2.
The diagram at the right should clarify this further,
help you remember the FOIL method,
as well as give a physical basis for this relationship.
(Remember also, the square root of (x2 + y2)
does NOT equal x + y.)
Consider extending the FOIL method first into trinomials:
(a + b + c)(d + e + f)
= ad + ae + af + bd + be +
bf + cd + ce + cf.
The distributive property is another way to consider this situation.
Here the box method is useful.
| d | e | f | |
|---|---|---|---|
| a | ad | ae | af |
| b | bd | be | bf |
| c | cd | ce | cf |
Now extend the method into three dimensions to find: V = (a + b)(c + d)(e + f) = ace + acf + ade + adf + bce + bcf + bde + bdf. This would be useful in finding the volume, which is why it is difficult to display in two dimensions.
By knowing the volume, one can determine the dimensions of a polyhedron. Specifically for a cube with edge s and volume s3, given a cube with volume 1000 cubic centimeters (1 liter), you can take the cube root to determine each side had length 10 centimeters or about 3.937 inches. Since one gallon is 231 cubic inches, it is thus about 3.785 liters. Other unit conversions can be expected and are summarized in Numbers lesson 9. Cube roots and volume are at the heart of an ancient impossible geometric construction from antiquity, the Delian Cube Doubling problem. Another important concept is that if you double the dimensions of a cube, the volume goes up by a factor of 8=23, just like area went up by a factor of 4=22. This is a problem commonly encountered when converting from cubic feet into cubic yards!
Example: Suppose you wish to pour concrete 4" deep in your driveway which is 90' long and 9' wide.
Answer: You quickly discover that there are 90×9÷3=270 feet3. However, there are only 10 yards3 since each yard is 3 feet and 33=27.
Calculating in the "native unit" of yards: 30×3÷9 can help prevent such an error. By "native" we mean here that the final results are expected in cubic yards. If the initial units are converted to yards fewer mistakes will be made. It is EXTREMELY common to erroneously divide by 3 or 9 and not 27 when converting cubic feet into cubic yards.
Example: Suppose you wish to find the volume of the square based right pyramid A-BCDE given in an earlier example with slant height 26" and base 20" on each side.
Answer: The height is 24" as calculated in the previous example. Thus the volume is (1/3)×B×h = (1/3) × 20" × 20" × 24" = 3200 in3.
| Prism or cylinder: V = base area × height |
| Pyramid or cone: V = (1/3) × base area × height |
Sphere: V = (4/3)![[pi]](pi.gif) × (radius)3 × (radius)3 |
Typically these formula are written as V=Bh (prism or cylinder),
V=(1/3)Bh (pyramid or cone), or
V=(4/3)![[pi]](pi.gif) r3 (sphere).
Note how a big B is used to signify that this is a two dimensional
base or area and not the same (linear) b we use in triangles.
r3 (sphere).
Note how a big B is used to signify that this is a two dimensional
base or area and not the same (linear) b we use in triangles.
Oblique Prisms and cylinders have the same volume as a right prism or cylinder with the same height and base area. Think of a stack of paper whose top has been pushed to one side. The stack is no longer vertical. However, the volume of paper hasn't changed. In the formula for finding the volume of an oblique prism please note that the height is the perpendicular segment between the top and bottom bases. When you learn calculus you will discover the surface area of a sphere to be the derivative with respect to r of the sphere's volume formula. A similar thing happens between area of a circle and its circumference. This may be happenstance or there may be a deep reason which I'd like to know.
Example: A favorite volume/surface area problem is as follows. A swimming pool is 24' long, 20' wide, 3' deep at the shallow end, and 10' deep at the deep end. The floor slopes evenly. What is the inside surface of the swimming pool and what is the volume (in gallons)?
Answer: The swimming pool is a trapezoidal prism. The floor is 25 feet long since 10' - 3' = 7' and 72+242 = 49 + 576 = 625 = 252. The surface area is the sum of 5 surfaces: 2 congruent trapezoidal sides (½(3+10)•24), 2 rectangular ends (3•20 + 10•20), and the bottom (20•25). This is 2•156 + 60 + 200 + 500 = 1072 feet2. The volume is Base × height, where Base is the area of one side (½(3+10)•24), and the height is the width of the pool (20). Thus the volume is 3120 feet3 or 23339 gallons (multiply by 123 cubic inches per cubic foot and divide by 231 cubic inches per gallon).
A gedanken experiment (thought experiment) used to justify the
volume formula for a sphere is as follows. First, remember the
circle area activity where we cut the circle into 16 wedges, then rearranged
the wedges into a r× r parallelogram.
Along the same lines, cut a sphere into pyramids.
The total area of the bases of these pyramids is
4
r parallelogram.
Along the same lines, cut a sphere into pyramids.
The total area of the bases of these pyramids is
4 r2.
The height of each is r.
Hence the formula is derived.
Along the same lines, some have suggested remembering the
1/3 in conal volume formulae by correlating it to the analoguous
two dimensional trianglular area formula which has a 1/2 in it.
r2.
The height of each is r.
Hence the formula is derived.
Along the same lines, some have suggested remembering the
1/3 in conal volume formulae by correlating it to the analoguous
two dimensional trianglular area formula which has a 1/2 in it.
Given two solids included between parallel planes. If every plane cross section parallel to the given planes has the same area in both solids, then the volumes of the solids are equal. This is know as Cavalieri's Principle.
The Greek
Archimedes
is one of the three greatest mathematicians of all time.
Among his important discoveries is the relationship between the volumes of
the cone, sphere, and cylinder. In fact, this discovery was so much his
favorite that he requested it to be inscribed on his
tombstone.
Specifically, consider a sphere of radius r,
two cones each with the same radius and height (r), and
a cylinder with the same radius and height (2r).
The cylinder will contain either the two cones or the sphere.
Their volumes can easily be seen to be (4/3)![[pi]](pi.gif) r3,
2(1/3)
r3,
2(1/3)![[pi]](pi.gif) r3, and
2
r3, and
2![[pi]](pi.gif) r3.
Thus the cones plus the sphere equals the cylinder exactly.
(Actually, Archimedes is more commonly credited with showing the
sphere's volume to be 2/3's that of the cylinder.)
See the corresponding diagrams in the textbook related to the proof
of Cavalieri's Principle.
r3.
Thus the cones plus the sphere equals the cylinder exactly.
(Actually, Archimedes is more commonly credited with showing the
sphere's volume to be 2/3's that of the cylinder.)
See the corresponding diagrams in the textbook related to the proof
of Cavalieri's Principle.
Example: Question 10.2#24 in our text asked the students about cones made from circles (radius 4") with central angles of 45°, 60°, and 120° removed (which got taped to the board amid Madonna jokes). Perform the following. Find the volume of each cone. Find the central angle which maximizes volume. Find the central angle which maximized volume to surface ratio.
Answer: For bonus points hand in your solution by the time the chapter reviews are due.
| BACK | HOMEWORK | ACTIVITY | CONTINUE |
|---|