|
Planes have no bumps and like lines go on forever. Three (noncollinear) points determine a plane. Three points also determine: a triangle; a line and a point not on the line; and two intersecting lines. Exactly one plane contains these. Thus a three-legged stool is stable, but more legs may cause a chair to wobble. Because lines have no thickness, planes also have no thickness. A line that is not in a plane can intersect the plane in at most one point.
| The measure of the smallest of all possible angles defines the angle measure between a line and a plane. |
|
If a line l intersects a plane X at point P, then
line l is perpendicular to plane X
(l |
| Line-Plane Perpendicular Theorem: If a line is perpendicular to two different lines at their point of intersection, then it is perpendicular to the plane that contains those lines. |
Two planes are parallel planes if and only if they have no points in common or they are identical. Again, this inclusive definition is not universally used. The distance between parallel planes is the length of a segment perpendicular to the planes with an endpoint in each plane. The distance between a plane and a point not on it is measured along the perpendicular segment from the point to the plane.
When two planes intersect, four dihedral angles are formed. The measure of these angles can be specified by constructing rays perpendicular to the line of intersection and measuring those angles formed. Skew lines are non-coplanar lines which do not intersect.
 Just as there is a difference between a polygon and a polygonal region,
we differentiate between the surface of a 3-D figure and the space
it encloses.
With this we start solid geometry.
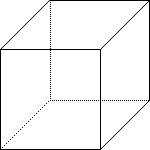
A box, the surface of a rectangular solid, or
parallelepiped is one of the most important 3-D figures.
A box has six faces each of which is a rectangular region.
Opposite faces lie in parallel planes.
A cube is a box with all faces square regions.
The edges are line segments where the faces meet each other.
The endpoints of the edges are the vertices.
A box has 12 edges and 8 vertices.
See the figure at the right for a typical 2-D representation
and
A tesserack or hypercube is a four dimensional analogue of a cube.
See the figure on the left for a 2-D representation of this 4-D object.
More information about these can be
seen and
found.
Many people have difficulty believing such can exist which is why such books as
Flatland
(Abbott, 1884),
Sphereland
(Burgers, 1983), and
Flatterland
(Stewart, 2001) were
written.
Just as there is a difference between a polygon and a polygonal region,
we differentiate between the surface of a 3-D figure and the space
it encloses.
With this we start solid geometry.
A box, the surface of a rectangular solid, or
parallelepiped is one of the most important 3-D figures.
A box has six faces each of which is a rectangular region.
Opposite faces lie in parallel planes.
A cube is a box with all faces square regions.
The edges are line segments where the faces meet each other.
The endpoints of the edges are the vertices.
A box has 12 edges and 8 vertices.
See the figure at the right for a typical 2-D representation
and
A tesserack or hypercube is a four dimensional analogue of a cube.
See the figure on the left for a 2-D representation of this 4-D object.
More information about these can be
seen and
found.
Many people have difficulty believing such can exist which is why such books as
Flatland
(Abbott, 1884),
Sphereland
(Burgers, 1983), and
Flatterland
(Stewart, 2001) were
written.
|
A cylindric solid is the set of points between a region and
its translation image in space, including the region and its image. A cylindric surface is the boundary of a cylindric solid. A cylinder is the surface of a cylindric solid with a circular base. A prism is the surface of a cylindric solid with a polygonal base. |
Cylindric solids have two bases which are congruent and in parallel planes. The surface excluding the bases is known as the lateral surface. The height or altitude is the distance between the planes of the bases. If the translation vector is perpendicular to the planes of the bases, the cylindric solid is a right cylinder or a right prism, otherwise it is oblique. Prisms are named by the shape of their base. The non-base faces of a prism are known as lateral faces which meet at lateral edges. A right prism whose base is a regular polygon is a regular prism.
|
A conic solid is the set of points on any segment between a region
(the base) and a point (the vertex) not in the plane of the
base. A conic surface is the boundary of a conic solid. A pyramid is the surface of a conic solid with a polygonal base. A cone is the surface of a conic solid with a circular base. |
Conic solids have but one base. Pyramids have lateral edges which connect vertices of the base polygon with the vertex. In a cone, the lateral edge is any segment whose endpoints are the vertex and a point on the base circle. The triangular, non-base, faces of a pyramid are lateral faces. Pyramids and cones can also be right or oblique. A right pyramid with a regular polygonal base is also regular. A cone also has an axis which is the line (not line segment) though the vertex and the center of the base. The height of a conic is the distance between the vertex and the plane containing the base. In a regular pyramid, slant height is the altitude of any lateral face (a triangle). Only in a right cone is this the same as the length of a lateral edge. A cone or pyramid may be truncated—many drinking glasses are truncated cones. A truncated cone is also known as a frustum.

|

|

|

|

| ||||||||||
| Frustum | Pyramid | Prism | Sphere | Torus |
| A sphere is the set of points in space at a certain distance (radius) from a point (center). |
Spheres have zero bases. A sphere may be thought of as the three-dimensional analogue of a circle. Twice a radius is a diameter. A Hypersphere or 4-ball is a four dimensional analog of a sphere. (Analogue is purposely spelt differently, but also correctly here.) A ball (circle, sphere, hypersphere) in n dimensions is termed an n-ball.
| A plane section of a three-dimensional figure is the intersection of that figure with a plane. |
A sphere and a plane can intersect in very few ways. First, the plane might only touch the sphere at a point. This plane must be tangent at that point thus the line containing the center of the sphere and the point of intersection would be normal (perpendicular) to the plane. Second, the plane intersects in more than one point in which case the intersection is a circle. This intersection is termed a small circle unless the plane contains the center of the circle, in which case it is known as a great circle. Great circles divide spheres into hemispheres, literally half spheres. Great circle routes are very important in navigation because they contain the shortest distance between two points on the surface. A geodesic is a general term for the shortest distance between two points. Metric is the term for this from general relativity. It is how we measure space-time. In differential calculus terms it is: dx2+dy2+dz2-c2dt2. Antipode the exact opposite or contrary; also points of a sphere, such as the earth, which are diametrically opposed (opposite ends of a diameter).
The earth is an oblate spheroid (shaped like an M & M, i.e. flattened at the poles and of the three mutually perpendicular radii, the longer is the repeated one). A prolate spheroid looks more like a football or cigar (of the three mutually perpendicular radii, the shorter is the repeated one). In an ellipsoid, the three mutually perpendicular radii are different lengths. See this site for some diagrams and definitions, including the torus or donut.
![[parabola, circle, ellipse, and hyperbola as conic sections]](conicsl.jpg)
Illustrated above are the intersection of a plane with a cone—a double napped cone. These loci (sets of points) are the conic sections. Loci is plural for locus (set of points). These conic sections (circle, ellipse, parabola, and hyperbola) will be studied more extensively in algebra II. See this web page for further details.
|
A Platonic Solid is a convex polyhedra with
all faces identical polygons. There are exactly five as proved below. |
| Polyhedron Name | Face Shape | Faces | Vertices | Edges | dual | 2-D Sketch | Ancient |
|---|---|---|---|---|---|---|---|
| Tetrahedron | Triangle | 4 | 4 | 6 | self | 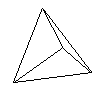 | fire |
| Hexahedron | Square | 6 | 8 | 12 | Octahedron | 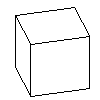 | earth |
| Octahedron | Triangle | 8 | 6 | 12 | Hexahedron | 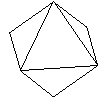 | air |
| Dodecahedron | Pentagon | 12 | 20 | 30 | Icosahedron | 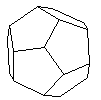 | cosmos |
| Icosahedron | Triangle | 20 | 12 | 30 | Dodecahedron | 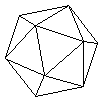 | water |
The Platonic Solids are also known as regular polyhedra. A tetrahedron is also known as a triangular pyramid. A hexahedron is also known as a cube. Duals are especially important in crystallography where the scattered radiation (electrons, neutrons, x-rays) is best studied in reciprocal space. As you look at the table above, please give thought to Euler's formula which relates the number of faces, vertices, and edges of any polyhedra: F + V = E + 2.
It can easily be shown that there are only five regular polyhedron (convex and faces all the same regular polygon). Consider how many identical regular polygons can come together at one vertex. We always need more than two if we are going to be able to fold it up and enclose any space. For triangles (with an angle of 60°) six would tesselate the plane. Hence three, four, and five must be considered and the results can be viewed above as the tetrahedron, octahedron, and the icosahedron. For squares (with an angle of 90°) four would tesselate the plane. Hence only three must be considered and the cube is the result. For pentagons (with an angle of 108°) four exceeds 360°. Hence only three must be considered and the dodecahedron is the result. Three hexagons (with an angle of 120°) tesselate the plane. Hence we are have exhausted the possibilities resulting in five regular polyhedra or platonic solids.
This link leads to a page describing the five platonic solids, complete with colored figures. This site has solids you can rotate. This site links to many other good sites. The ancients related the five platonic solids with fire (4), earth (6), air (8), water (20), and the cosmos (12).
|
In an Archimedian Solid, the solid is convex, all vertices are identical, all faces are regular polygons, but not all identical. |
The Archimedian Solids can be classified by a set of numbers which specifies the number of sides in the polygons at each vertex. Thus {3,6,6} would indicate one triangle and two hexagons at each vertex. The other twelve are: {3,8,8}; {4,6,6}; {3,10,10}; {5,6,6}; {3,3,4,4}; {3,3,5,5}; {3,4,4,4}; {4,6,8}; {3,4,4,5}; {4,6,10}; {3,3,3,3,4}; and {3,3,3,3,5}. This (broken) link leads to a page describing the thirteen Archimedian or semi-regular Solids, complete with colored figures.
C60 is a highly symmetrical molecule of pure carbon. The shape is the same as that of a soccer ball or the Archimedian Solid the truncated icosahedron: {5,6,6}. C60 is often referred to as Buckyballs. Technically, this Archimedian Solid is a Truncated Isocahedron. This name is derived from Richard Buckminster Fuller, renowned for his geodesic domes. The Stepan Center at Notre Dame is a local example. C60 is one of a class of compounds known as Fullerenes also name after the American architect above. The C60 molecule was discovered in 1985 while a group was trying to understand the absorption spectra of interstellar dust. Their worked earned them the 1996 Nobel prize in chemistry. Initially produced in only tiny amounts, or extracted from soot, it is now readily available and is the center of a lot of varied research. Long tubes of carbon called nanotubes have also been produced. C60 represents a new, unexpected crystalline form of solid carbon. The other forms: tetrahedronal carbon bonding in diamond and the sheet type bonding in graphite have much longer histories. See this page for a brief, well documented history of C60.

My research interests deal with triplication of pentominoes from a subset of 9 of the 12. Can you triplicate all 9 in the set or even all 12? Can you triplicate a given pentomino with all 220 subsets?
Architects often draw scaled views or building plans. Some may term these elevations. This site has nets for many solids and other use tidbits.
|
A net is a 2-dimensional figure that can be folded on its segments or curved on its boundaries into a 3-dimensional surface. |
 How many colors are necessary and how many colors are sufficient to color any map on a plane?
On a sphere (4)?
On a Möbius Strip (6)?
On a Torus (7)?
Maps with boundaries consisting only of straight lines or circles
may need even fewer colors! (See figure right.)
Except for the plane/sphere, these questions were
easy to answer.
How many colors are necessary and how many colors are sufficient to color any map on a plane?
On a sphere (4)?
On a Möbius Strip (6)?
On a Torus (7)?
Maps with boundaries consisting only of straight lines or circles
may need even fewer colors! (See figure right.)
Except for the plane/sphere, these questions were
easy to answer.
Like a net, a map is a 2-D approximation for a 3-D figure.
When it is a map of the earth, various distortions are common.
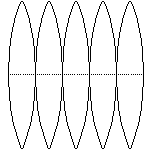 If you took a globe, sliced it about every 15° of longitude,
the resulting gores (see figure left) could be laid flat. This would be
fairly accurate, but rather inconvenient—different parts of
the same country would be on different gores and the actual shape
of these countries difficult to see.
Historically, the Mercator projection, created by
the Flemish cartographer in 1569, is commonly used.
Land areas near the poles are especially distorted—leading to
an Africa (11 million miles2) the size of Greenland
(less than 1 million miles2).
This occurs because the Mercator projection is actually the net
for a cylinder, not a sphere. The transformation can be generated by extending
rays from the center of the earth onto the lateral face of a cylinder.
As indicated above, this transformation is not an isometry.
However, it does preserve betweenness and collinearity,
on the lines of longitude and latitude.
Thus the four directions (north, south, east, and west)
are on perpendicular lines.
If you took a globe, sliced it about every 15° of longitude,
the resulting gores (see figure left) could be laid flat. This would be
fairly accurate, but rather inconvenient—different parts of
the same country would be on different gores and the actual shape
of these countries difficult to see.
Historically, the Mercator projection, created by
the Flemish cartographer in 1569, is commonly used.
Land areas near the poles are especially distorted—leading to
an Africa (11 million miles2) the size of Greenland
(less than 1 million miles2).
This occurs because the Mercator projection is actually the net
for a cylinder, not a sphere. The transformation can be generated by extending
rays from the center of the earth onto the lateral face of a cylinder.
As indicated above, this transformation is not an isometry.
However, it does preserve betweenness and collinearity,
on the lines of longitude and latitude.
Thus the four directions (north, south, east, and west)
are on perpendicular lines.
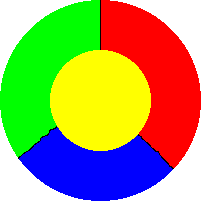 After studying maps, Francis Guthrie in 1852 conjectured that any
map on a sphere or plane could be distinguished/colored with
only four colors. It is easy to see that four colors are necessary (see right).
However, proof of the sufficiency part was only completed in 1976.
Even then, the proof supplied by Haken and Appel was controversial
for many years. The controversy arose because they used a computer
to help prove only four colors were necessary
for each of the 1952 types of possible maps. The problem was embedded in
graph theory
before this analysis.
After studying maps, Francis Guthrie in 1852 conjectured that any
map on a sphere or plane could be distinguished/colored with
only four colors. It is easy to see that four colors are necessary (see right).
However, proof of the sufficiency part was only completed in 1976.
Even then, the proof supplied by Haken and Appel was controversial
for many years. The controversy arose because they used a computer
to help prove only four colors were necessary
for each of the 1952 types of possible maps. The problem was embedded in
graph theory
before this analysis.
| Four-Color Theorem. Suppose regions which share a border of some length must have different colors. Then any map of regions on a plane or sphere can be colored in such a way that only four colors are needed. Conjectured by Gutrie in 1852; proved by Haken and Appel in 1976. |
Below is a handout for homework problem 9.8#26. (Somewhere add angle of inclination/declination and a graphic for dihedral angles.)
| BACK | HOMEWORK | ACTIVITY | CONTINUE |
|---|