Back to the Table of Contents

Applied Statistics - Lesson 2

Organizing and Presenting Data

Lesson Overview

There are a wide variety of ways to summarize, organize, and present data. Most of the common methods, such as stem-and-leaf diagrams, frequency distributions, histograms, bar, and other graphs, will be summarized here, along with the usual conventions and terms for each.

Coding Data

It is common practice to code data by assigning numerical values to nonnumeric measurements. An example might be to code gender as 1's and 2's instead of "male" and "female". The choice of 1 for male and 2 for female is rather arbitrary, but might correspond to the number of X-chromosomes in each somatic cell. One reason for data coding is to conserve storage space which historically was at a premium. (A keypunch card only held 80 bytes. Flat it is about the size of of a CD-ROM, rolled up it is about the size of a thumb drive, either of which easily holds half a gigabyte or so!) Another reason is that there are no upper and lower case [arabic] numbers. A computer may not register "male" as equal to "Male" or even "MALE". As computer storage costs have declined and computer software sophistication has increased, this practice may be in decline, but the concept remains important.

Data must somehow be entered into a computer before it can be analyzed. Optical scan sheets might be used or the data keyed in using a [micro]computer. Most statistical packages can import data, but comma separated, quote delineated, or fixed length fields are expected.

Various file editors can be utilized but the concept of a data record akin to a punch card is becoming an archaic concept. If one were to use a word processor, "hard returns" may be necessary and a fixed pitch font might help determine that the data is aligned into the proper columns. These programs generally allow the export of "flat ASCII" or ".txt" type files. (The alternative to ASCII (EBCDIC) is becoming a historic footnote as well.)

Spreadsheet programs have become a common way to enter data. As stated in the syllabus, however, they do not replace statistical packages for analyzing data. Generally there are no statisticians employed in the creation of spreadsheet programs, there is no warranty, implied nor expressed, regarding the validity of its statistical output, so time is probably better spent otherwise!

Exploratory Data Analysis

A recent trend in statistics has been the use of exploratory data analysis. It is a fundamentally different approach to analyzing data. Historically, statistics were used to confirm final conclusions about data. Some very important assumptions were made, calculations were complex, and graphs often unnecessary. The modern emphasis has been more on exploring data, trying to simplify the way the data are described, and gain deeper insights into its nature. Few assumptions are made, the calculations are simple, as are the graphs. The next two plot types (stem-and-leaf and box-and-whiskers) are modern in their approach.

Stem-and-Leaf Diagrams

John Tukey in the late 1970s developed many techniques for Exploratory Data Analysis, one of which, the stem-and-leaf diagram, has become especially popular. A stem-and-leaf diagram has the advantage of retaining the data in its original form, but providing a visual representation. Illustrated below is the U.S. Presidential Inauguration age data. In this case, the stem, the tens portion of the president's age, is given on the left, and the leaf, the units portion of the president's age, is given on the right.

4 | 23667899
5 | 0111112244444555566677778
6 | 0111244589

Please note that the separation line should be continuous, but time constraints limited accomplishing that feat. The following rules should be observed when constructing stem-and-leaf diagrams.

  1. The leaves on the right should be in increasing (or decreasing) order, left to right.
  2. No commas should appear on the right.
  3. No horizontal lines should appear.
  4. If the stem/leaf break occurs at a decimal point, put the decimal point to the left with the stem.
  5. If the leaf is double or triple digit, etc., leave a [half] space between each entry.
  6. There should be at least five but no more than twenty rows.
  7. If a range is used for the stem, an asterisk (*) may be used to separate the corresponding leaves.
Reformatting the above with more rows (called by some books splitting the stem) emphasizes even more its normally distributed nature. Notice how the stem-and-leaf diagram is also somewhat like a histogram, but turned on its side. Normally, data are rounded before being put into such a diagram, but ages, for whatever reason, usually get truncated! Many common statistical packages will generate stem-and-leaf diagrams.

4 | 23
4 | 667899
5 | 0111112244444
5 | 555566677778
6 | 0111244
6 | 589

Boxplots

A boxplot or box and whiskers plot is a visual representation of the 5-number summary and will thus be covered in lesson 3.

Frequency Tables or Distributions

A frequency table lists in one column the data categories or classes and
in another column the corresponding frequencies.

A common way to summarize or present data is with a standard frequency table as seen in the fictitious salary data given below. A stem-and-leaf diagram for this data would be rather pointless!

ProfessionSalary (in $)frequency
Teacher36,0001,000,000
notebook assembler360,000100,000
Netscape® programmer3,600,000100
Windows® programmer36,000,00010
Bill Gates360,000,0001

Some authors abbreviate frequency with the letter f. Frequency refers to the number of times each category occurs in the original data. Often, the category column will have continuous data and hence be presented via a range of values. In such a case, terms used to identify the score (class) limits, exact limits (class boundaries), class intervals (class widths), and interval midpoints (class marks) must be well understood. For the following examples, we will use the split stem presidential inauguration data from the stem-and-leaf diagram above.

Score limits (class limits) are the largest or smallest numbers which can actually belong to each class.

For this example, the score limits are 40 and 44 for the smallest class and 65 and 69 for the largest class. Each class has a lower score limit and an upper score limit.

Exact limits (class boundaries) are the numbers which separate classes.
They are equally spaced halfway between neighboring score limits.

For the presidential inauguration data the exact limits would be 39.5, 44.5, 49.5, 54.5, 59.5, 64.5, and 69.5. Note that 39.49999... is another name for and identical with 39.50000..., but emphasizes it as a left-handed instead of a right-handed limit.

Interval midpoints (class marks) are the midpoints of the classes.

For this example, the interval midpoints are 42.0, 47.0, 52.0, .... It may be necessary to utilize interval midpoints to find the mean and standard deviation, etc. of data summarized in a frequency table. This is because information often has been lost and we make two important assumptions: 1) the scores are uniformly distributed between the exact limits of the interval; 2) Whenever a single score is used to represent a class interval, the interval's midpoint will be utilized.

Class interval (class width) is the difference between two exact limits (class boundaries) (or corresponding score/class limits).

For this example, the class width is 5.0. Following are guidelines for constructing frequency tables.

  1. The classes must be "mutually exclusive"—no element can belong to more than one class.
  2. Even if the frequency is zero, include each and every class.
  3. Make all classes the same width. (However, open ended classes may be inevitable.)
  4. Target between 5 and 20 classes, depending on the range and number of data points.
  5. Keep the limits as simple and as convenient as possible (multiple of width?).
  6. If practical, make the width odd so that the interval midpoint is a whole number.

If your limits are not immediately obvious based on the data, try to find an appropriate width by rounding up the range divided by the number of classes. Your lower limit should be either the lowest score, or a convenient value slightly less. Avoid irrelavent decimal places. Large data sets justify having more classes. One published guide is: number of classes = 1 + log2n. This gives you 5 classes for small data sets of 12 to 22 elements and 10 classes for larger data sets of 362 to 724 elements. The seven classes used above for 50 elements is right on target. It is not uncommon to omit empty classes—be alert for such guideline violations! Omitted classes do not change the class width, but can be a real source of confusion!

Relative freqency tables contain the relative frequency instead of absolute frequency.

Relative frequencies can be expressed either as percentages or their decimal fraction equivalents.

Cumulative frequency tables contain frequencies which are cumulative for subsequent classes.

In a cumulative frequency table, the words less than usually also appear in the left column.

Graph of Data

Pictures of data can help answer questions about how data are distributed. These pictoral representations are often called graphs from the Greek word "to write or draw." Such graphs are very common, such as the hourly or daily stock market average or federal interest rates and are now a standard part of the middle school math curriculum. In both cases, the horizontal or x-axis (or abscissa) is time (an independent variable). The vertical or y-axis (or ordinate) is the dependent variable. The axes intersect at the origin which has the ordered (x,y) pair (0,0).

The x-axis often represents ordinal data. The equal differences between values can tend to imply interval data when such is not the case. Use care when evaluating such a graph. If you look at a graph of the Dow-Jones Industrial Average you will quickly note that the y-axis has been exaggerated and the small range of values of recent interest are magnified. Proper protocol requires the y-axis to be broken with a pair of short parallel oblique lines before it mets the x-axis.

Ordered pairs of (x,y) data points can be plotted either in isolation or by connecting the points. When the points are connected the term data curve is used. The curve, however, may well be composed of straight-line segments and so does not correspond with the popular usage of this word.

Since the scales of measurement along the axes can be quite arbitrary, graphs can easily be used to support even opposite points of view. A new rule to me that helps avoid distortion and provide consistency is to use an aspect ratio of 4:3 for the horizontal:vertical axes' lengths. This has been called by some the three-quarter-high rule. Examples of graphs, including bar graphs and scatterplots, will be discussed below.

Histograms

The term histogram comes from the Greek words meaning web and write. As such it is a way to untangle data. Another name for a histogram is a bar graph or bar chart, although some texts differentiate between the two. (A bar graph is used when the independent variable is nominal.) In a histogram the vertical axis has the frequency, while the horizontal axis has the intervals. No gaps are allowed between the bars, unless the independent variable is nominal. The distribution of the data: normal, skewed left, skewed right, should be fairly obvious from a bar graph. Histograms are quite commonly used to visually display frequency and relative frequency charts. Again, some texts indicate that a bar graph is used for catagorical data and require gaps between the bars. Illustrated below are a bar graph and the accompanying TI-83+ settings for the US presidential inauguration data.

[bar graph of inauguration data]           [window settings 42-x-69]           [stat plot 1 on L1 barchart]

A relative frequency histogram has the same shape and horizontal scale as a histogram, but the vertical scale is now the relative frequency.

A Pareto chart is a bar graph for qualitative data.

The bars in a pareto chart should be arranged in descending order of frequency, from left to right.

Frequency polygons are similar to histograms, but use line segments to connect the points.

When construction a frequency polygon, the class marks should be used on the horizontal scale. The graph should also be extended to the left and right so that it begins and ends with a frequency of 0.

Cumulative frequency polygons, also known as ogives, are also commonly encountered.
The line in an ogive (pronouced "oh-jive") will always go up to the right (have nonnegative slope).

Pie Charts, etc.

Pie charts (circle graphs) are a common way to understandably display the relative proportions of the various data elements. This is most commonly used on unranked or qualitative data. If this is done by hand, you should use a protractor to accurately measure your angles. Remember that there are 360° in a full circle. Use proportions to convert frequencies to angles: %/100 = degrees/360°.

A pictograph depicts data by using pictures of an object, such as coins, money bags, airplanes, etc. Those which use multiple objects the same size are ok. Those which use similar objects, scaled linearly to represent data, can easily distort things. There may be many other variations, but those listed above are most common.

Scatterplots

Data for two quantitative variables can be graphically displayed in a scatterplot. In the homework you will be asked to make a scatterplot of the U.S. presidential inaugural age data. The value of the x is inferred from the data's position within the list with Washington number 1 and the other W 43. The data given (age) will be treated as the dependent variable (y). If trends such as president being elected younger or older existed they should be evident. Analyzing such trends will be covered later under correlation.

Distribution Shapes

The shape of a distribution has very important consequences. Historically, grades were often given based on a curve, specifically the normal curve whereby there were mostly C's, several D's and B's, and few F's and A's. Harvard I think it was, in recent years, has limited the number of A-type grades given. In 2003-04 I think it was 50% and in 2004-05 it was 35%. They are thus forcing a change in the shape of the distribution of grades.

Distributions which may have some arbitrary large values, such as home valuations, but many small values, are termed positively skewed. Distributions which may have the opposite characteristic, such as the Harvard grade distributions, where most are high and only a few are low, are termed negatively skewed.

A distribution may be uniform (such as the probability of getting any particular pip count when rolling one die) or symmetric (such as the probability of getting any particular pip sum when rolling a pair of dice). In fact, the uniform distribution given above is also symmetric. In a symmetric distribution there is a line of symmetry such that if the graph were folded the two sides would coincide.

The most common distribution shape is heap-shaped or mound-shaped, looking like someone just took a basket of something and dumped it out. If the mound spreads out a lot (like water!) the degree of peakedness or kurtosis is low and the distribution is said to be platykurtic. A uniform distribution is platykurtic. If the mound piles up like a stalagmite, the distribution is said to be leptokurtic. The reference standard is the normal distribution and how peaked a distribution is about the mean in comparison. The images below are from Gosset via Harnett (1975). The shape of a distribution is extremely important and will be considered extensively throughout the rest of this course.
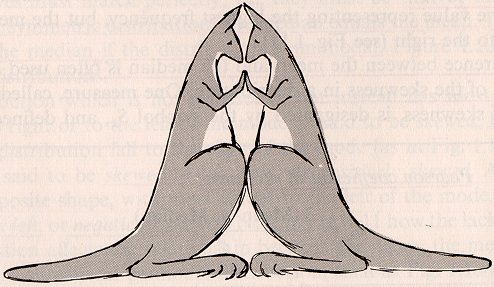
Short-tailed platykurtic. Long-tailed leptokurtic.

BACK HOMEWORK NO ACTIVITY CONTINUE