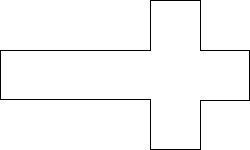
 A common puzzle for finding area is show at the right.
Assume all angles are right angles.
Suppose you know the overall length and width to be 5 in. and 3 in.
respectively. What is the perimeter?
A common puzzle for finding area is show at the right.
Assume all angles are right angles.
Suppose you know the overall length and width to be 5 in. and 3 in.
respectively. What is the perimeter?| Perimeter is the sum of the lengths of all sides of a region or polygon. |
Perimeter is a one-dimensional measurement. It is one way to measure the size of something. Formulae abound, but for triangles and quadrilaterals they are so straight-forward as to be rather trivial. The more sides there are of equal length, the simpler the formula. Thus for squares with four equal sides of length s, the perimeter is equal to 4s. In fact, for any regular n-gon with sides of length s the perimeter is equal to ns. For rectangles or kites which have only two different side lengths, say x and y, the perimeter is equal to 2x + 2y. Often the sides of a rectangle are referred to as its length and width.
The word parameter is so often interchanged with perimeter that we shall compare and contrast them here. Parameter: an arbitrary constant each of whose values characterize a member of a system [as a family of curves]. Thus we see perimeter can be one parameter describing a circle, hence much of the confusion. Recall that we also used the word parameter in conjuction with statistics and population.
Consider how you might measure the perimeter of an irregularlly shaped object, say, a kidney shaped swimming pool.
Answer: Possibly lay a rope along the perimeter and then measure the length of the rope. Hopefully, this will be a good enough approximation. If not, solving such problems is one of the reasons calculus was invented!
Irregularly shaped regions can have very large perimeters relative to their area. In fact, rectangles with an area of 100 units2 can vary in perimeter from as small as 40 units (each side of 10 units) to virtually infinite, if its length is virtually infinite and its width is infintesimal. What is, for example, the perimeter of a rectangle with width 0.01 units and area 100 square units?
Answer: Since A = lw (see below) and A = 100 and w = 0.01 are given, 100 = l×0.01. Dividing both sides by 0.01 (and applying symmetry) gives l = 10000. Thus the perimeter is 20000.02 units. Note the casual dropping of units during calculation, but specification of units in the end. You will generally get away with this in geometry, but in chemistry and physics specifying units and properly converting between them will be very helpful in solving problems.
While we are on the topic of units, now is a good time to stress some important information. Specifying units is very important in science. Wrong assumptions about units can be very costly. See these write ups about the 1/8 billion dollar Mars Orbiter in Sep. 1999. In fact, recent discoveries have lead to the conclusion that inconsistant units, (Inv. & Tech., Spring 2003, page 11) not only the weather, was an important factor in the English defeat of the Spanish Armada in 1588. We will start earnestly deducting points if units are omitted (or wrong). The world and science uses MKS or SI (metric) whereas most American citizens commonly think in English units. How and when this will change is a good subject for debate! Numbers Lesson 9 provided many useful conversions, especially noting useful ones between the two systems.
Our textbook is not very good about specifying units so often the generic term units will be used. As mentioned previously, the textbook also omits the degree symbol (°) which in my experience is problematic for students going on to precalculus and calculus (all our students) where angle measurements without units are assumed to be in radians. On this topic I note here again my disagreement with the authors.
 A common puzzle for finding area is show at the right.
Assume all angles are right angles.
Suppose you know the overall length and width to be 5 in. and 3 in.
respectively. What is the perimeter?
A common puzzle for finding area is show at the right.
Assume all angles are right angles.
Suppose you know the overall length and width to be 5 in. and 3 in.
respectively. What is the perimeter?
Answer: We can note that all the horizontal top sides sum to 5" as do the bottom, and all the vertical left sides sum to 3" as do the right. Thus the perimeter is 16" even though the figure might not otherwise be to scale!
| Area is the two-dimensional measurement of the interior of a polygon or other region. |
As we transition into area we will be using square units extensively. These are often specified using the English notation: square feet (sq. ft.) or the metric notation m2 or some combination thereof. However, students have a tendancy to mix the feet (') and inch (") designations with the metric notation and I take a VERY dim view of the result: 36"2. ONLY 36 sq. in. or 36 in2 are acceptable notations. Test points are at stake here so please refrain (and not by singing a sad song) from utilizing this shortcut.
A common way to measure area, or the space covered by a region, is to tessellate it with a fundamental region, often using a grid, count the number of such regions used, (in whole or in part), then multiply by the area of each fundamental region to obtain the area. For irregularly shaped regions this will be an approximation or estimate. The actual area will be the limit this estimate approaches as the grid size decreases. The limit concept will be formally developed in calculus.
Some units are inherently units of area, for example, the acre or hectare. An acre originally was the area a man could plow in a day with a yoke (pair) of oxen. Now it has been standardized as 1/640'th of a square (statute) mile. Thus one acre is 43,560 square feet (52802/640). This corresponds with a square about 208.7 feet on a side. However, 330'×132' (or perhaps 220'×198') would be more commonly encountered since the mile is/was typically divided in half repeatedly (5280'/16=330') or built up from rods (16.5') or chains (4 rods). The hectare is 100 are. Each are is 100 m2. Thus a hectare is 10000 m2 = (39.37 in/m÷12 in/ft)2÷43,560 ft2/acre=2.471 acres. A common mistake involving area occurs when solving the following problem: How many square yards are there in a room 9' by 12'.
Answer: 9'÷3'/yd=3 yds; 12'÷3'/yd=4 yds; 3 yds × 4 yds = 12 sq. yds. The problem occurs when students multiply 9'×12'=108 ft2 and then divide by only 3 instead of 9 ft2 per yd2. Such mistakes extend into volume problems as well. In general, if you double the length of the sides (perimeter), the area quadruples (2×2=4) and the volume goes up by a factor of 8=2×2×2. Please bear this important fact in mind.
The text lists four postulates about area as follows.
|
|
| ||||||
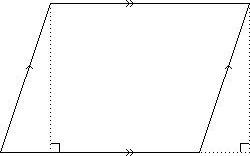
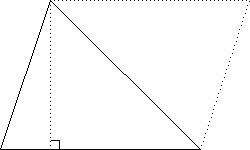
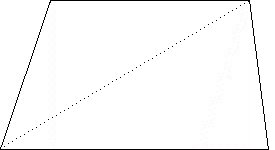
| Parallelogram with moved triangle | Triangles with altitude | Trapezoid as two triangles |
| Square: | A = l2, length squared |
| Rectangle: | A = l × w, length times width |
| Parallelogram: | A = b × h, base times height (since a parallelogram can be manipulated into a rectangle.) |
| Triangle: | A = ½bh, where b is the base, and h is the height. (Two congruent triangles can be manipulated to form a parallelogram.) |
| Trapezoid: | A = ½(b1 + b2)h. (A trapezoid can be broken down into two triangles.) |
| Kite: | A = ½AC×BD, where AC and BD are the lengths of the diagonals (A kite can be broken down into four right triangles.) |
| Regular polygon: | A = ½asn = ½ap, where a is the apothem, s is the length of each side, n is the number of sides, and p is the perimeter. |
(Do diagrams for 32=22+5 and 52=12+13, etc.)
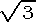 .
The area of each triangle will be
½bh=½(2)(
.
The area of each triangle will be
½bh=½(2)(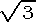 )=
)=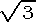 .
Thus the total area will be 6
.
Thus the total area will be 6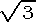 .
Questions involving regular hexagons are ubiquitous on standardized tests
and contests.
.
Questions involving regular hexagons are ubiquitous on standardized tests
and contests.
It is usually easiest to bound the octagon in a square and subtract off the
four corner triangles. We can quickly calculate the sides of these
isosceles right triangles to be 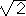 . Thus the total
area is given by
(2+2
. Thus the total
area is given by
(2+2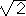 )2-4(½)
)2-4(½)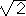
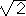 .
We will leave the task of simplifying this to 8(
.
We will leave the task of simplifying this to 8(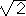 +1)
to the reader. We will note an alternate method involving trigonometry.
Divide the octagon into eight triangles using the vertices and center.
Each triangle is isosceles with base angles of 135º/2=67.5º.
The tangent function gives the ratio of the opposite side to the adjacent
side in a right triangle. Thus tan 67.5º gives the height
of this triangle since when we bisect the triangle we get a right triangle
with base of one. tan 67.5º=
+1)
to the reader. We will note an alternate method involving trigonometry.
Divide the octagon into eight triangles using the vertices and center.
Each triangle is isosceles with base angles of 135º/2=67.5º.
The tangent function gives the ratio of the opposite side to the adjacent
side in a right triangle. Thus tan 67.5º gives the height
of this triangle since when we bisect the triangle we get a right triangle
with base of one. tan 67.5º=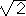 +1.
This also gives a method for an approximate answer for any regular
n-gon.
+1.
This also gives a method for an approximate answer for any regular
n-gon.
Example: A concrete driveway is to be 90' long, 9' wide, and 4" thick.
Calculate the number of cubic yards of concrete needed, two ways,
first by converting these numbers into yards and second by
calculating the volume in cubic feet and then converting.
Compare your results and then estimate the cost based on a
5.5 bag limestone mix, with 5# of fiberglass reinforcing fibers per yard,
at $75/yard3.
Answer: The driveway is 30 yards long, 3 yards wide, and
Example: My 10 acre corn field is a 1/4 mile long. How wide is it? Answer: Solve the proportion: 10/640=1320x/52802 for x=330'. This would be a long 10 acres instead of a square 10 acres. In this case it was the W ½ of the W ½ of the NE ¼ of the NW ¼ section 15, Sherman township (Town 20 North, Range 9 West), in Michigan.
Example: A 24' long by 16' wide swimming pool angles down uniformly from shallow (3') to deep (10'). Find the area of the bottom and sides of the pool. Answer: the bottom forms the hypotenuse of a 7-24-25 right triangle, so the bottom is 16'×25'=400 ft2. The ends are rectangles 3'×16'=48 ft2 and 10'×16'=160 ft2. The sides are trapezoids with bases 3' and 10' and height 24' or 2•½•(3'+10')•24'=312 ft2. The total surface area is thus: 920 ft2.
Example: A triangle has sides with lengths 8, 15, and 17. What is the altitude to the longest side? Answer: We first note that 82+152=64+225=289=172 and thus we have a right triangle. The area is then ½•8•15=60 units2. Any altitude can be used as a height though so A=60=½•x•17. From which we discover: x=60/17 or about 7.06. See also 8.5#20.
Example: An isosceles trapezoid has bases of 10" and 16" and a 36" perimeter. What is its area? Answer: We find the length of the missing sides by subtracting the bases from the perimeter and dividing by two: (36"-10"-16")/2=5". Then we note how (16"-10")/2=3" is the side of a triangle whose other side is the height and hypotenuse is this 5" side. We immediately recognize the 3-4-5 right triangle and can find the area as: ½(10"+16")•4"=52 in2.
![[circle folded into sixteenth's, cut, reassembled as parallelogram]](circarea.gif) Circumference is the word used instead of perimeter for the
distance around a circle. It is a one directional synonym, however.
The ancients searched hard for a way to find the circumference of a circle
given its radius or diameter. This search is the history of
Circumference is the word used instead of perimeter for the
distance around a circle. It is a one directional synonym, however.
The ancients searched hard for a way to find the circumference of a circle
given its radius or diameter. This search is the history of
|
C = |
The length of an arc of a circle can be easily determined via a
proportion relating the whole circle circumference
(2 r or 360°) to the fraction you have.
Radians were also introduced in Numbers Lesson 14.
The measure of a central angle in radians corresponds to its arc length
for a unit circle (a circle with r = 1).
r or 360°) to the fraction you have.
Radians were also introduced in Numbers Lesson 14.
The measure of a central angle in radians corresponds to its arc length
for a unit circle (a circle with r = 1).
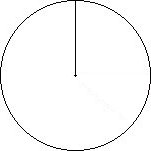
Circle was defined in Lesson 2. The terms center and radius were used in the definition. A minor arc is a portion of a circle less than a semicircle. The notation for a minor arc is very similar to that for line segments. However, instead of a straight line above the two endpoints, a curve is used (concave downward). A semicircle is exactly half a circle. A major arc is a portion of a circle equal to or more than a semicircle. The notation for semicircle and major arc is similar to that of minor arc. However, three points are used to emphasis size and establish direction. To establish a major arc as a semicircle some additional notation would be required.
What is a lune? (See page 486.)
|
|
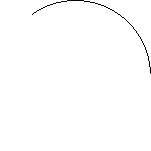
|
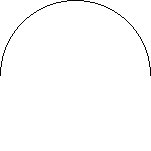
|
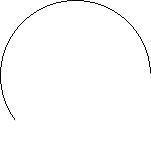
| ||||||||||
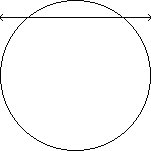
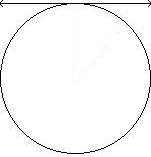
| Radius | Diameter | Minor Arc | Semicircle | Major Arc |
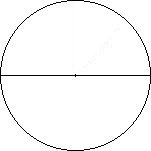
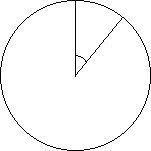
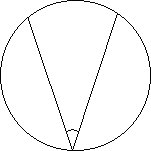
A chord is a line segment with endpoints on a circle. A diameter is a very special chord containing the center. A secant is a line containing a chord. A tangent is a line intersecting a circle exactly once. It does so in such a way that the radius to that point forms a pair of right angles. Secants and tangents will be discussed further in Geometry Lesson 14 and are important terms for side length ratios in trigonometry. A central angle is formed by two radii. An inscribed angle is formed by two chord which intersect on the circle. The measure of an inscribed angle is half the measure of the corresponding central angle (intercepted arc).
The center is not technically part of the circle but rather part if its interior. A sector of a circle is the region between an arc and two radii of a circle. A segment of a circle is the region between an arc and a chord of a circle. An annulus is the region between two concentric circles. You can find a similar construct by taking the first two and last two letters. A disk is a circular region or the interior of a circle.
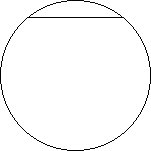
|
|
|
|
| ||||||||||
| Chord | Secant | Tangent | Central Angle | Inscribed Angle |
|
|

|

|

| ||||||||||
| Center | Sector | Segment | Annulus | Disk |
Page 485 gives Hero's or Heron's Formula for finding
the area of a triangle. The Greek mathematician Hero[n] of Alexandria
died about 50 A.D. His formula is based on the
semiperimeter or half the perimeter, where if a, b,
and c are the sides, s = ½(a + b + c).
The area is then:
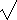 (s(s - a)(s - b)(s - c)).
(s(s - a)(s - b)(s - c)).
Another method of finding the area of a triangle can be applied, again, if the vertices are lattice points. That would be to use right triangles to complete a rectangle and subtract the excess.
One last triangle area formula is: ½bcsin A, where b and c are two sides and angle A is the angle between them. This formula is related to the cross product, something we will study with vectors.
| BACK | HOMEWORK | ACTIVITY | CONTINUE |
|---|