 ABC
ABC 
 DEF has a very
precise meaning. It succinctly summarizes the six statements
(assume lines atop these segments): AB
DEF has a very
precise meaning. It succinctly summarizes the six statements
(assume lines atop these segments): AB DE,
BC
DE,
BC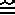 EF, AC
EF, AC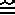 DF,
DF,
 A
A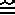
 D,
D,
 B
B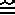
 E, and
E, and
 C
C
 F.
It is very important to maintain the vertices in the proper order.
Not doing so is a common mistake.
F.
It is very important to maintain the vertices in the proper order.
Not doing so is a common mistake.A typical proof using triangle congruence will use three steps to set up the three congruent triangle parts (several may be givens), a fourth step invoking a triangle congruence theorem, followed by a CPCF (Congruent Parts of Congruent Figures are congruent) invocation to relate additional congruent triangle parts. This kind of proof is very similar to those using transitivity in that regard and lend themselves nicely to the two column format. However, outside geometry most proofs are written in paragraph style. Our text advises against including givens to cut down on thoughtless ritual. (Thus they deduce conclusions instead of making statements.) However, as a visual learner, I tend to disagree with the authors on this one. It can often be a useful way to organize what you know, making it easier to fill in what you don't. Thus we will be flexible in format and advise students to try a variety of approaches until they find what suits them. In this chapter the two column proof reigns supreme, however.
Below we will discuss the three triangle non-congruences of AAA, and SSA=ASS further. First we will discuss the four triangle congruences of SSS, SAS, SAA (which is the same as and is usually referred to as AAS), and ASA.
SSS is more formally known as the Side-Side-Side Triangle Congruence Theorem (or maybe Edge-Edge-Edge Triangle Congruence Theorem).
| If in two triangles the three sides are pairwise congruent, then the triangles are congruent. |
As with much of our textbook, it proves this using transformations (reflections preserve distance and the Kite Symmetry Theorem). This is important because it differs from Euclid's faulty superposition development. It also differs from other modern rigorous developments which use SAS as a postulate (Hilbert, Birkhoff). Whichever route you take to develop YOUR geometry, you should also be able to convince yourself using only a compass and straight-edge that SSS always yields congruence. The two triangles might have opposite orientation, but they will still be congruent. As implied by the faulty development of Euclid on this score, the proof of these triangle congruence theorems is more involved than the proofs we expect you to be able to write. However, we do expect you to be able to follow the proofs given. The SsA Triangle Congruence Theorem is the longest in our text and does not appear in many texts, including Euclid's Elements.
We spoke earlier about the 3-4-5 triangle being a right triangle. Of course, not all 3-4-5 triangles are going to be congruent because someone might use 3 attometers, 3 miles, or even 3 light-years. However, because of the Pythagorean Theorem these are all right triangles. (Personally, I have reservations about both attometers and light-years due to quantization of space-time and general relativity.) This is a fundamental property that given the three sides of a triangle, you have fixed the angles. This relates as well to the fact that triangles are rigid. Rigidity is an important property in the functionality of objects like doors, rafters, and gates.
SAS is more formally known as the Side-Angle-Side Triangle Congruence Theorem. Be sure the angle you are using is BETWEEN the two sides you are using. If sides AB and BC are used, angle B is the included angle. Order is important and is implied by the order the letters are specified.
| If in 2 triangles 2 sides and the included angle are pairwise congruent, then the triangles are congruent. |
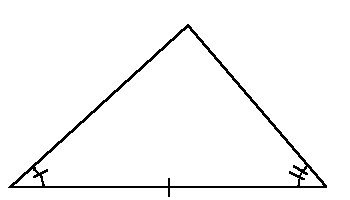
AAS is more formally known as the Angle-Angle-Side Triangle Congruence Theorem. The side used here is opposite the first angle.
| If in 2 triangles 2 angles and a non-included side are pairwise congruent, then the triangles are congruent. |
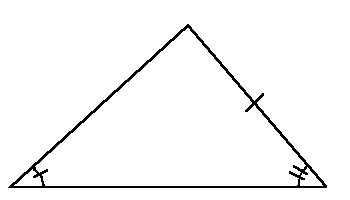
ASA is more formally known as the Angle-Side-Angle Triangle Congruence Theorem. The side used here is BETWEEN the two angles you are using. If angle A and angle B are used, side AB is the included side.
| If in 2 triangles 2 angles and included sides are pairwise congruent, then the triangles are congruent. |

|

| ||||
| ASA Triangle | AAS Triangle |
There is a fundamental difference between ASA and AAS
which isn't readily apparent to the beginning geometry
student. Consider the two triangles given above.
Notice how the given side is between the two angles in the ASA triangle,
whereas the given side is opposite one of the angles in the AAS triangle.
| If in two triangles two angles are pairwise congruent, then the triangles are similar. |
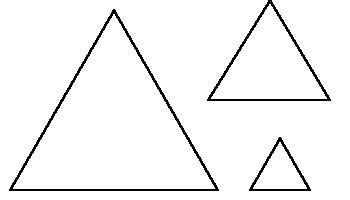
There is NO SSA Triangle Triangle Congruence Theorem. (Although SSA and ASS are equivalent, please avoid the latter spelling, even though it fairly represents the situation should you invoke it.) This is what we refer to as the ambiguous case or SSA condition. You can think of condition as being like a disease. Please refer to the diagram above and note the following. Angle A is fixed (given). Side length AB is fixed (given). Side length BC is also fixed (given). However, there are two possibilities for C as indicated by where a circle centered at B intersects line AC. One is denoted Ca and the other Co. Ca results in an acute angle at C whereas Co results in an obtuse angle at C. (The opposite type of angle is formed at B, thus the triangle is always nonacute.) As long as BC is longer than the minimum distance between B and AC and shorter than AB, two triangles are possible. However, if BC is longer than AB only one triangle is possible (see SsA below). If BC is exactly equal to the minimum distance between B and AC, then only one triangle, a right triangle, is possible (see HL below). If BC is less than the minimum distance between B and AC, then no triangle is possible.
Just like there can be zero, one, or two solutions to a quadratic equation, there can be zero, one, or two triangles corresponding to a given SSA triple. This deeper connection is made more explicit by examining the quadratic nature of the Law of Cosines, a generalization of the Pythagorean Theorem.
| Law of Cosines: In triangle ABC with sides of length a, b, and c: c2 = a2 + b2 - 2abcosC. |
Side a of length a=BC is opposite  A,
side b of length b=AC is opposite
A,
side b of length b=AC is opposite  B, and
side c of length c=AB is opposite
B, and
side c of length c=AB is opposite  C.
Notice how the Law of Cosines as stated is symmetric in a and
b—they can be interchanged with the same result.
Which angle/side is used is also arbitrary, so we could just as well
have written it as: a2 =
b2 + c2 -
2bccosA or
b2 =
a2 + c2 -
2accosB.
Since the cos 90°=0, in a right triangle the Pythagorean Theorem results.
Traditionally, in a right triangle, angle C is right and side c is
then the hypotenuse. Thus the boxed statement of the law of cosines has
additional merit.
C.
Notice how the Law of Cosines as stated is symmetric in a and
b—they can be interchanged with the same result.
Which angle/side is used is also arbitrary, so we could just as well
have written it as: a2 =
b2 + c2 -
2bccosA or
b2 =
a2 + c2 -
2accosB.
Since the cos 90°=0, in a right triangle the Pythagorean Theorem results.
Traditionally, in a right triangle, angle C is right and side c is
then the hypotenuse. Thus the boxed statement of the law of cosines has
additional merit.
| If in two triangles two sides and the angle opposite the longer of the two sides are pairwise congruent, then the triangles are congruent. |
Second, if BC is exactly equal to the minimum distance between B and line AC, then angle C is a right angle. BC and AC are then legs of this right triangle and AB is the hypotenuse. Notice how if BC were slightly longer, two triangles would result and it if were slightly shorter no triangle is possible. This is commonly referred to as the HL Triangle Congruence Theorem.
| If in two right triangles the hypotenuse and a leg are pairwise congruent, then the triangles are congruent. |
Other texts note that the SSA condition guarantees congruence if the congruent angles are nonacute (i.e. right or obtuse). With information at the end of this chapter (Law of Sines, etc.) it will be seen that these are equivalent. Note also how the HL Congurence Theorem is also a subset of SAS for right angles.
With the AAS triangle congruence theorem we can now prove the converse of the Isosceles Triangle Base Angles Theorem or the converse of pons asinorum.
| If two angles of a triangle are congruent, then the sides opposite these angles are congruent. |
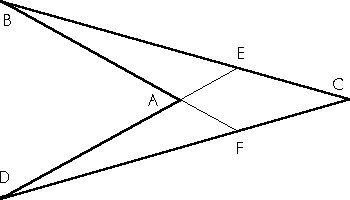
Consider the kite ABCD at right. Note how triangles BCF and DCE both have the region AECF in their interiors. They thus overlap. Angle C is in common to both. Thus if we are given two additional pieces of information we may be able to prove these triangles congruent. You might consider what two pieces are required. Diagonals in regular polygons present similar situations.
The question often comes up as to how many triangles are formed by the diagonals in a polygon, perhaps regular. The answers for the triangle (1) and quadrilateral (8) border on trivial, but get rather involved for the pentagon, hexagon, etc. If you can find the value for a pentagon, this link will give you the answer for n > 5. Specifically, the sequence known as A006600 is for regular polygons and the sequence A005732 is for cyclic (inscribable in a circle) n-gons. Curiously, for n odd they are the same, whereas for n even they differ. This paper explains why.
There are shapes other than triangles which we can use to cover a region. When using general shapes the term tesselate is used. A tesselation uses a fundamental region to completely cover (or tile) a plane such that no holes are found. This fundamental region is repeated via the various isometries (translation, rotation, reflection, glide reflection), hence they are all congruent. A regular polygon will tesselate only if the angle measure evenly divides 360°. Thus only the following regular polygons tesselate: triangles (60°), squares (90°), and hexagons (120°). Any triangle and any quadrilateral will tesselate because you can arrange them so that angles summing to 360° surround each vertex. However, only a few pentagons will tesselate and several new types were only recently discovered. Hexagons are likewise restricted.
M. C. Escher (1898-1972) was a recent Dutch artist who often utilized tesselations and other mathematical concepts, such as perspective in his works. The following link has a nice set of links to various tesselation sites and this one has a java applet useful for online study. A couple of these have contest deadlines in the March 28-April 1 range. Tesselmania demo. Tessel mania examples. Tess 1.51.
In addition to the standard definition (two pairs of parallel sides), there are additional properties which are sufficient conditions to conclude that a given quadrilateral is a parallelogram. These are as follows:
| An angle is an exterior angle iff it forms a linear pair with an interior angle of a [convex] polygon. |
Note: there are alternate definitions of exterior angle which may make just as much sense, but which violate the UCSMP limitation of angles being less than or equal to 180º. Please be clear which definition we are using.
Since an exterior angle of a triangle forms a linear pair with an interior angle, and that interior angle is supplementary to the sum of the other two interior angles, the following two theorems should be fairly self-evident. Please note that we refer to an exterior angle not the exterior angle since there are two possible exterior angles at each vertex.
|
The measure of an exterior triangle angle is equal to the sum of
the measures of the interior angles at the other two vertices
(Exterior Angle Theorem). The measure of an exterior triangle angle is greater than the measure of either of the interior angles at the other two vertices (Exterior Angle Inequality). |
This chapter concludes with two theorems about the lengths of sides in triangles. Specifically, the longer sides are opposite the larger angles. The text uses two theorems (Unequal sides/angles Theorems), and many nots to make this statement. This is actually a specific case of the Law of Sines given below. For nonobtuse triangles, since sine is a monotonic (always increasing or always decreasing) function between 0° and 90° it is easy to see how this works. For obtuse triangles one must also rely on the unequal angle theorem above and have deeper insight into the sin function.
|
Law of Sines: In triangle ABC with sides of length a,
b, and c: sin A/a = sin B/b = sin C/c or a/sin A = b/sin B = c/sin C. |
These concepts are also often referred to as the Hinge Theorem. This basically states that given two fixed length sides in a triangle, the length of the third side will increase as the angle opposite increases, just like the set of triangles described by a hinge.
| BACK | HOMEWORK | ACTIVITY | CONTINUE |
|---|