 ABC
ABC
 DEF
this means that
DEF
this means that
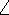 A
A
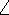 D,
D,
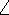 B
B
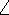 E, and
E, and
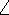 C
C
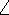 F.
It also means AB = DE, BC = EF, and
AC = DF.
In writing this last statement we have also utilized the
Segment Congruence Theorem below (since html does set overlines easily).
F.
It also means AB = DE, BC = EF, and
AC = DF.
In writing this last statement we have also utilized the
Segment Congruence Theorem below (since html does set overlines easily).
He then set out to prove geometric properties of figures by deduction rather than by measurement. He is credited with at least five theorems: 1) diameters bisect circles; 2) base angles in isosceles triangles are equal; 3) vertical angles are equal; 4) angles inscribed in a semicircle are right; and 5) ASA triangle congruence. He also found the correct number of days in a year and predicted at least some aspects of the solar eclipse of 585 B.C. Proofs were certainly well established by the time of the Pythagorean School (5th century B.C.) but were usually written in paragraph form.
The two-column proof is very modern, first appearing in Geometry textbooks about 1900. This was thus soon after Peano axiomized the natural numbers; Dedekind's cut defined the reals; Hilbert reaxiomized Geometry in his Grundlagen Der Geometrie in 1899; and in general, Whitehead and Russell set out to axiomize all of mathematics. Two-column proofs serve as a way to organize a series of statements (the left hand column), each one logically following from prior statements. The justifications (the right-hand column) can be definitions, postulates (axioms), properties of algebra, equality, or congruence, or previously proven theorems. Just as with our definitions, circularity is to be avoided!
Historically, geometry and proof were virtually synonymous. Euclid's Elements was the first careful development of geometry and served as a basis not only for learning the subject for 2,000 years but also as a way to develop the powers of higher reasoning. These powers of higher reasoning are expected in such high paying professions as doctors, lawyers, computer programmers, and engineers. It is also at the cornerstone of our democracy, trial by jury, and innocent until proven guilty, where guilt beyond reasonable doubt is to be established. This has become controversial especially in cases with minimal evidence such as O. J. Simpson and Scott Peterson.
As geometry has become a cornerstone of the high school mathematics curriculum, educators have questioned this approach with some suggesting the adolescent mind as being incapable of reasoning at this level of abstraction. Thus geometry textbooks of the last few decades have relegated proof to the very end or watered down their approach. Since calculus is still commonly taught in a rigorous, proof-based manner, and higher mathematics even more so, such an approach does not adequately serve the needs of students who will continue their mathematical development through the calculus. It is with these concerns that the Math and Science Center approach has emphasized proof while utilizing the UCSMP geometry text. While the UCSMP geometry is written at a level to be taken by the top 10% in eighth grade, we use it at the ninth grade level. These students (both the top 10% and our Center students who are drawn from this population) are all expected to complete Calculus during their senior year in high school. We thus must collapse/backload four years of Geometry, Algebra II, FST (Functions, Statistics, and Trigonometry), and Precalculus with some discrete math topic (number theory, logic, history) into the three years of our freshman, sophomore, and junior curricula.
The text gives three reasons to write proofs: 1) people sometimes disagree; 2) unexpected results can be verified; and 3) some things cannot be proven or are not even true. It also breaks the proof of a conditional p=>q into four components as follows: 1) the Given (p); 2) the To prove (q); 3) a Drawing (which might be omitted); and 4) the Argument whereby q is shown to follow p. We will often label the givens as step zero (0). Gleason, who helped solve Hilbert's fifth problem is quoted in the book The Honors Class on page 150 saying: "Proofs really aren't there to convince you that something is true—they're there to show you why it is true."
| If two figures are congruent, then any pair of corresponding parts are congruent. |
It is extremely important to remember when writing a congruence statement
that order is important. If one thus writes
 ABC
ABC
![]()
 DEF
this means that
DEF
this means that
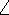 A
A
![]()
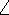 D,
D,
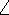 B
B
![]()
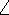 E, and
E, and
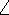 C
C
![]()
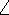 F.
It also means AB = DE, BC = EF, and
AC = DF.
In writing this last statement we have also utilized the
Segment Congruence Theorem below (since html does set overlines easily).
F.
It also means AB = DE, BC = EF, and
AC = DF.
In writing this last statement we have also utilized the
Segment Congruence Theorem below (since html does set overlines easily).
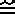 , ~,
, ~, 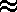 , and
, and  (equal, congruent, similar, approximately equal to, and equivalent).
(equal, congruent, similar, approximately equal to, and equivalent).Congruent objects are virtually ubiquitous. Your chairs, lecture notes, and coins are but three common examples of congruent—or nearly congruent objects. As nearly as physicists can determine, all electrons are exactly identical. Eli Whitney, the inventor of the cotton gin in 1793 is also credited with the invention of interchangeable parts when he made a large number of guns by machine for the government. Before that time, parts were hand-made and thus field maintenance frustrating. Interchangeable parts depends on the concept of congruence. Ironically, these two inventions were major causes of the American Civil War, the one by making cotton such a widely grown commodity, the other by industrializing the North. Eli Whitney was a pioneer in the industrial revolution. Whitney died long before this in 1825 after suffering several years with an enlarged prostate. His self-treatment with a catheter or stent greatly relieved his pain. It has been said that all men, if they live long enough, are guaranteed to experience prostate problems. Tomatoes (lycopene) and now onion/garlic/etc. have been shown to delay or defer the onset of such problems. Some have noted the lack of congruence in human anatomy with some accounts cruder than others.
|
Every isometry preserves Angle measure, Betweenness, Collinearity (lines), and Distance (segment length). |
Just like the equivalence properties of equality, we have Equivalence Properites of Congruence. We will state these also without proof.
|
For any figures F, G, and H: F 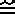 F.
Reflexive Property of Congruence F.
Reflexive Property of CongruenceIf F 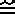 G,
then G G,
then G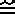 F.
Symmetric Property of Congruence F.
Symmetric Property of CongruenceIf F 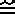 G and
G G and
G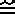 H, then
F H, then
F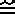 H.
Transitive Property of Congruence H.
Transitive Property of Congruence
|
(Any operator with these three properties is known as an equivalence relation and such status confers an important role upon an operator.)
The following two theorems (Segment and Angle Congruence) also follow directly.
|
Two segments are congruent if and only if they have the same length. Two angles are congruent if and only if they have the same measure. |
Every conclusion in a proof needs justification. A list of some useful justification already encountered is given below. However, we must emphasize, a diagram is often an essential, though controversial part of a proof. I say controversial since diagrams are not necessarily drawn to scale and only certain things can be assumed about them. Often, too much has been assumed from them and it was the late 1800's before Pasch made clear errors dating back to Euclid. Hilbert had no aversion to diagrams, however.
| Segment Congruence | Angle Congruence |
|---|---|
|
|
When generating proofs, sometimes we know what we want to prove and must carefully outline justifications which prove it. The book calls this justfiying a conclusion that has been asserted. At other times you have a variety of information available and are left to explore possible outcomes. The book calls this making a justified conclusion from given information.
Given:  A with radius AB, A with radius AB,
 B with radius BA, B with radius BA, A intersects A intersects  B
at C and D B
at C and DTo Prove:  ABC is equilateral. ABC is equilateral.
|
| Conclusions | Justifications |
|---|---|
|
|
We can also prove several important additional theorems using the transitive property. Please review the definitions of alternate interior and alternate exterior angles as given in lesson 3.
| Two lines cut by a transversal are parallel if and only if alternate interior angles are congruent. |
Please examine the proof given in the book for both parts of this biconditional, completing the missing justifications. Note how they included the givens as step 0 in the proof. They also include the proof of the following theorem as a homework exercise. You can expect to often use the Vertical Angle Theorem, Transitive Property, and Corresponding Angle Theorem in your proofs.
| Two lines cut by a transversal are parallel if and only if alternate exterior angles are congruent. |
| Points on the perpendicular bisector of a segment are equidistant from the endpoints of the segment. |
The construction of a regular pentagon has been relagated to an activity, as has the "construction" of a(n) heptagon. Please be sure to look at them.
| Through a point not on a line, there is exactly one line parallel to the given line. |
The text elevates the above postulate (Playfair's Parallel Postulate) to the status of a theorem (Uniqueness of Parallels Theorem) by proving it. We have already alluded in lesson 1 to the assumptions inherent in the postulates (Corresponding Angles) used in this textbook which allow this to happen. It is a restatement of Euclid's fifth postulate and is the basis of Euclidean Geometry. Although Euclidean Geometry is a good approximation on a local and macroscopic level, it is not the geometry of the universe we live in, either in the large-scale or perhaps in the microscopic.
| The sum of the interior angles in a triangle (in Euclidean Geometry) is 180°. |
The interior angle at a vertex in a polygon is the angle formed by the the two sides at that vertex. For concave polygons we specify that the interior of the polygon is a subset of the interior of the angle.
Now consider an arbitrary quadrilateral (four-sided polygon) with a diagonal. The diagonal splits the quadrilateral into two triangles. From this it should be clear that the sum of the angles in any quadrilateral is 360°. (If the quadrilateral is convex, the diagonal must be chosen carefully!) Now consider an arbitrary (convex) n-gon. From one vertex extend diagonals to all other vertices. There will be n-3. This is because we cannot draw a diagonal from one vertex to itself, nor to either of its two neighbors. This procedure generates n-2 triangles. Technically, a proof would be much more difficult if we were to include non-convex polygons, but we will state the following without any restrictions. Our textbook would have real problems with this since the measure of the interior angles in a non-convex polygon would exceed 180°!
| The sum of the interior angles in an n-gon is (n-2)•180°. |
| BACK | HOMEWORK | ACTIVITY | CONTINUE |
|---|
