| A plane figure is reflection-symmetric if and only if there is a line which reflects the figure onto itself. This line is a symmetry line for the figure. |
The capital letters A, B, C, D, E, H, I, K, M, O, T, U, V, W, X, and Y are often written as reflection symmetric figures. Some are symmetric about a horizontal line (BCDEHIKOX) whereas others are symmetric about a vertical line (AHIMOTUVWXY). As you can see since some are in both lists (HIOX), there may be more than one line of symmetry. A challenge would be to find words such as DIXIE or COOKBOOK composed entirely of letters with a horizontal line of symmetry or MOM, WAXY, YOUTH (written vertically!) composed entirely of letters with a vertical line of symmetry. After collecting enough of these words you might make them into a crossword puzzle (for extra credit)!
Our textbook states and proves what they call the Flip-Flop Theorem: (reflection is symmetric).
| If F and G are points/figures, and rl(F)=G, then rl(G)=F. |
From this it can be proved that every segment has two lines of symmetry: itself and its perpendicular bisector. This is the same as the letter I discussed above. Angles only have one line of symmetry: the angle bisector which causes one ray to reflect onto the other ray. A circle has infinitely many lines of symmetry (no matter which way you draw the diameter, the semicircles are reflections of each other). The section concludes with the following important result.
| If a figure is symmetric, then any pair of corresponding parts under the symmetry are congruent. |
Rorschach inkblots and logos commonly are reflective-symmetric. These symmetries will be useful when applied to various polygons. Symmetry is also important in algebra. The function y=x2 defines a parabola in which the sign of x doesn't matter. This makes it an even function (the exponent of 2 is another clue).
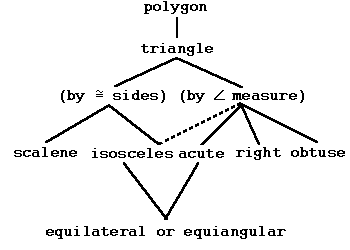Triangles, as mentioned in
Numbers lesson 11 and
Geometry lesson 2,
can be classified either by
the number of sides with the same length
(0 is scalene, 2 or more is isosceles, all 3 is equilateral)
or by the largest angle (acute, right, obtuse).
A hierarchy chart combining both situations is given at the left.
Due to the overlap, hierarchy charts for either situation
are typically given instead.
Note: a right/acute/obtuse triangle might be either scalene or isosceles.Also, our definition of isosceles includes and does not exclude the equilateral triangle. Just as there are special names associated with the sides of a right triangle (hypotenuse and legs), there are special names associated with the angles and sides of an isosceles triangle. The angle determined by the two equal sides is called the vertex angle. The side opposite the vertex angle is called the base. The two angles opposite the equal sides are the base angles (and are equal). These can also be described as the angles at the endpoints of the base.
Three important theorems are as follows.
Certain terms will be defined further below.
|
The line containing the bisector of the vertex angle
of an isosceles triangle is a symmetry line for the triangle. |
|
In an isosceles triangle, the bisector of the vertex angle, the perpendicular bisector of the base, and the median to the base determine the same line. |
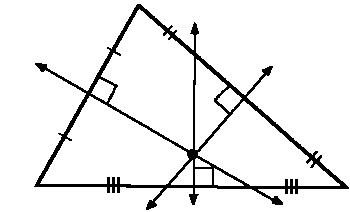
| If a triangle has two congruent sides, then the angles opposite them are congruent. |
| Every equilateral triangle has three lines of symmetry. These are the bisectors of the angles/sides. |
| If a triangle is equilateral, then it is equiangular. |
A corollary (a theorem which logically follows immediately from another theorem) is that the angles of an equilateral triangle are all 60°. Although the line of symmetry of an isosceles triangle is an angle bisector, median, perpendicular bisector, and an altitude, in most triangles, these lines are different.
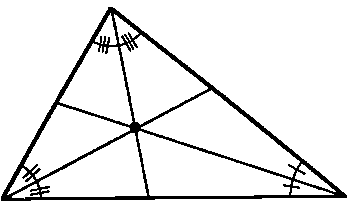
| A ray is an angle bisector if and only if it forms two angles of equal measure with the sides of the angle. |
| The three angle bisectors of a triangle are coincident at the incenter. |
The incenter is equidistant (distance r) from all three sides of a triangle. Thus if a circle were drawn with the incenter as its center with a radius r, it would be inscribed in the triangle.
| A segment, ray, or line is a perpendicular bisector (of a segment) if and only if it contains the midpoint of the segment and is perpendicular to the segment. |
| The three perpendicular bisectors of a triangle are coincident at the circumcenter. |
The circumcenter is equidistant (distance r) from all three vertices of a triangle. Thus if a circle were drawn with the circumcenter as its center with a radius r, it would circumscribed the triangle.
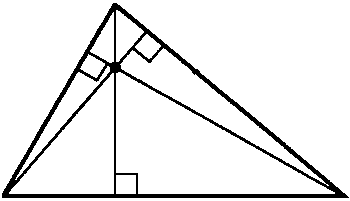
| A segment is an altitude if and only if it is perpendicular to the line containing the side opposite a vertex and contains that vertex. |
Altitude can also refer to the length of the segment described above. Trapezoids also have altitudes. In addition, the height of the 3-dimensional objects: prisms, cylinders, pyramids, and cones is termed altitude.
| The three altitudes of a triangle are coincident at the orthocenter. |
The orthocenter need not be in the interior of a triangle. It will be located inside only if the triangle is acute. If the triangle is right, the orthocenter will be on the hypotenuse. If the triangle is obtuse, the orthocenter will be outside the triangle.
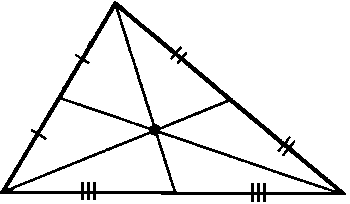
| A segment is a median of a triangle if and only if it connects one vertex to the midpoint of the opposite side. |
| The three medians of a triangle are coincident at the centroid. |
If the triangle were made of a uniformly dense material, the centroid would be the center of mass or center of gravity of the triangle. A thin solid object in this shape would balance at this point. Thus if a triangle is hung by a vertex, a line toward the local point of graviational attraction (local nadir or straight down) would describe a median and go through the centroid. Medians also have another important property.
| Medians always divide each other into a 1:2 ratio, with the larger portion (2/3) toward the vertex and the smaller portion (1/3) toward the opposite side. |
| The circumcenter, orthocenter, and centroid are always collinear. This line is called the Euler Line. |
In an isosceles triangle, all four of these points are collinear. In an equilateral triangle, all four are coincident.
An interesting construction is the Nine-point circle, the circle which goes through the midpoints of each side, the base of each altitude, as well as the midpoint of the segments between the orthocenter and each vertex.
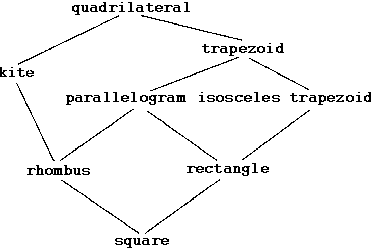Quadrilaterals can be classify by the lengths of their sides and how many
pairs of sides are parallel. Familiarize yourself with the hierarchy
chart at left. Remember that any property held by all figures of one type
is held by all types connected below it.
| A quadrilateral is a kite if and only if it has two distinct pair of consecutive sides congruent. |
This name should be familiar from the shape of the scientific instrument allegedly used by Benjamin Franklin, which are now used primarily as toys. An arrowhead, or the Startrek chevron is typically in the shape of a nonconvex kite. Another common name for this shape is dart. The vertices shared by the congruent sides are ends. The line containing the ends of a kite is a symmetry line for a kite. The symmetry line for a kite bisects the angles at the ends of the kite. The symmetry diagonal of a kite is a perpendicular bisector of the other diagonal.
| A quadrilateral is a trapezoid if and only if it has at least one pair of sides parallel. |
Some books define trapezoids as having exactly one pair of parallel sides, so beware. The parallel sides in a trapezoid are called bases. In a trapezoid, consecutive angles between pairs of parallel sides are supplementary.
| A trapezoid is an isosceles trapezoid if and only if it has base angles which are congruent. |
If follows directly that the sides opposite the congruent angles in an isosceles trapezoid are congruent. In an isosceles trapezoid, the perpendicular bisector of one base is also the other base's perpendicular bisector. This bisector is thus also a line of symmetry.
One of my favorite questions uses an isosceles trapozoid. If we give the height of an isosceles trapozoid, as well as the length of its two bases, it is possible to find its perimeter. Example: suppose we know a certain isosceles trapozoid has bases of 10 and 16 with height 4. We know that right triangles are formed outside the rectangular region defined by the height and shorter base. The right triangles have a base of 3 and height of 4 thus hypotenuse of 5. Hence the perimeter is 36. The triangles formed need not be integer and we will continue with area in a later lesson.
| A quadrilateral is a parallelogram if and only if both pair of sides are parallel. |
| A quadrilateral is a rectangle if and only if all angles are congruent. |
| A quadrilateral is a rhombus if and only if all sides are congruent. |
| A quadrilateral is a square if and only if all sides and all angles are congruent. |
| A plane figure F is rotation-symmetric if and only if there is a rotation (strictly) between 0° and 360° such that R(F)=F. The center of R is the center of symmetry for F. |
A figure is said to have n-fold rotational symmetry if n rotations each of magnitude 360°/n produce an identical figure. The last rotation returns it to its original position. A figure can have rotational and reflective properties separately or together. A figure with reflective properties can have rotational symmetry if and only if the lines of symmetry intersect.
Going back to our letter examples, H, I, O, X had two intersecting lines of symmetric and thus both reflective and rotational symmetry. The letters N, S, and Z have rotational symmetry but not reflective symmetry. Certain letters (M & W, b & q, d & p, n & u, h & y? or 4??) rotate into the other of the pair!
A polygon can be either equilateral or equiangular without, necessarily, being both (regular). The rectangle is an example of an equiangular quadrilateral, and the rhombus is an example of an equilateral quadrilateral. Neither has to be a square. However, for 3-gons, as stated in the theorem above, an equilateral triangle must also be equianglar.
| In any regular polygon, a point termed the center is equidistant from all vertices. |
| The distance from the midpoint of a side of a regular polygon to the center is the apothem. |
The apothem may also refer to the segment with length as describe above. The apothem is often used in some formulas. For example, the area of a regular polygon is A=asn/2, where a is the apothem, s is the length of each side, and n is the number of sides. Since p=sn or the perimeter is the number of sides times the length of each side, it can also be written A=ap/2.
| Every regular n-gon has n lines of symmetry and n-fold rotational symmetry. The lines of symmetry are all either angle bisectors or perpendicular bisectors of each side (or both if n is odd). |
The measure of the internal angles of a regular n-gon can be found as follows. Triangulate the polygon by drawing the n-3 diagonals from one vertex to all other vertices. This divides the n-gon into n-2 triangles. The angles of any triangle sum to 180°. Thus the internal angles of any n-gon sum to (n-2)•180°. The internal angles of a regular n-gon will be (n-2)•180°/n. We gave the formula for the number of diagonals of an n-gon in lesson 2 as n•(n-3)/2. You might consider further how many different lengths these diagonals might be, especially in a regular polygon.
| BACK | HOMEWORK | ACTIVITY | CONTINUE |
|---|