Back to the Table of Contents
A Review of Basic Geometry - Lesson 4
Mirror, Mirror…: Reflections and Congruence
Lesson Overview
Transformations, Congruent Transformations, Isometries
Many modern high school geometry textbooks, including UCSMP,
motivate similarity and congruence
through the use of transformations and isometries.
In fact, further study in high school mathematics and especially
various branches of higher mathematics are simplified by a
basic understanding of the symbolism and terminology of such mappings.
Specifically, the notation of forming the composition of functions
is identical to that used here. Also, the restrictions on functions
to guarantee their inverse is a function can perhaps be best
seen when treated as mappings.
 The alternative is to adopt something like SAS triangle
congruence (see chapter 7) as an axiom.
Either will be at the heart of a proof of the Isosceles
Triangle Theorem (then base angles are equal) or its converse
(then sides are equal) known as Pons Asinorum,
which
is
Latin for bridge of fools (or asses). This term has come to
mean any problem which severely tests the ability of an
inexperienced person.
The alternative is to adopt something like SAS triangle
congruence (see chapter 7) as an axiom.
Either will be at the heart of a proof of the Isosceles
Triangle Theorem (then base angles are equal) or its converse
(then sides are equal) known as Pons Asinorum,
which
is
Latin for bridge of fools (or asses). This term has come to
mean any problem which severely tests the ability of an
inexperienced person.
Similarity means to have the same shape.
Congruence means to have the same shape and measure.
|
A transformation is a mapping (correspondence) between points.
Each point in the preimage must have a unique image point
(one-to-one) and each point in the image must have exactly one
preimage point (onto). In algebra, equations are a form of
transformation from one variable to another. The equation
y = 2x + 1 maps x into y and the equation
specifies how each value of x corresponds with y. (This
particular mapping can be inverted: x = ½(y - 1).)
Similar mappings can be done with sets of points or figures.
Certain properties of a figure are preserved by some transformations.
Formally these are contained in a Reflection Postulate.
|
Specifically, Angle measure, Betweenness, Collinearity,
and Distance are preserved by all isometries.
|
These can easily be remembered by their first letter sequence: ABCD.
(Our textbook elevates this to theorem status,
but a careful look at its foundation might be revealing.)
Breaking the word isometry down into its root pieces indicates
the meaning "equal measure".
There are only four transformations which are isometries.
Another name for an isometry is a congruence transformation.
Some purists define congruence as follows.
Two figures F and G are congruent figures,
written F ![[is congruent to]](congru.gif) G, G,
if and only if G is the image of F under an isometry.
|
Note the symbol used for congruence:
![[is congruent to]](congru.gif) .
It combines the symbolism of equality (=) and
similarity (~).
.
It combines the symbolism of equality (=) and
similarity (~).
We will discuss the four isometries in detail next.
Mirror, Mirror.... What do you see when looking in the mirror? The exact
copy of your figure but reversed. When you raise your right hand, the mirrored
image raises its left. We refer to the original figure (you) as the
preimage and the copied version as the image.
If points on the image are labelled, then an apostrophe after the label
refers to the corresponding image points. Thus A' (read A prime)
is the image of point A.
The line of reflection or reflecting line is where the
reflection takes place. Think of a pond reflecting the landscape.
If this is a picture,
the surface of the water is the line of (symmetry) reflection.
If it is the real McCoy,
it will be a plane of reflection.
The line of reflection is always halfway between corresponding
preimage and image points.
A point Q is the reflected image of point P
over line l if and only if l is the
perpendicular bisector of segment PQ (assuming points
P and Q are not on line l).
|
This tells us how to locate and draw an image given its corresponding preimage.
We suggest using differently colored pencils
for the image and preimage for clarity.
A MIRA™ device is a semitransparent plastic tool which
partially reflects an image. It has a squared base and
flat surface which extends perpendicular to the paper.
This allows you to then quickly locate image points.
In addition to the ABCD properties listed above which are preserved,
is the property of orientation.
If you are facing east and looking in a mirror, your reflected image
is looking west. Reflection reverses orientation.
This corresponds with another name for reflection: flip.
A figure and its reflection are termed oppositely congruent.
If in turn the image is reflected again, orientation reverses again.
This doubly reflected image is now directly congruent with
the original image.
Polygons are said to have a clockwise orientation if your right
hand is toward the interior as you proceed from one vertex to
the next in the order specified, otherwise its orientation is
counterclockwise.
The British use the term anticlockwise.
This definition works whether or not the polygon is convex.
It should also be noted that the shortest distance between a point and a
line is along the perpendicular from the line through that point.
In symbols we represent the reflection of point P
(that is P')
over a line l as rl(P)=P'.
It is very common to reflect figures over the x- and y-axes.
This will be noted as: rx-axis or
ry-axis.
It should readily become clear that
rx-axis(x,y)=(x,-y) and
ry-axis(x,y)=(-x,y).
It should also be clear that a double reflection over the same line
would result in an identity transformation:
rl°rl(F)=F.
Another way to note this composition of transformation would be:
rl(rl(F))=F.
Note that in general the order is important and the one on the right
gets performed first.
(The little circle (°) should be slightly lower than it is.)
Many objects come in left and right orientations. Examples include
shoes, gloves, baseball mitts, bowling balls,
light bulbs,
etc.
One of the great mysteries of biochemistry is why one
chiral
orientation of the carbon in organic molecules predominates.
Louis Pastuer's famous separation of tartaric acid salt
crystals in the 1840's marks the beginning of such understanding.
(There were clearly two different, mirror configuations of
crystals and one rotated light one way, where as the other
rotated light the other. The mixture didn't rotate light at all.)
Parity nonconservation is the fact that the laws
of physics are not ambidextrous or reflexive symmetric.
Specifically, the weak force, (not gravitational, not electromagnetic,
nor the strong force between quarks), violates parity maximally.
All neutrinos are left-handed (well, that isn't clear now that they
have a very small mass). Instead of reflection, however, we
generally represent the parity operator (P) using space inversion:
(x, y, z)
is transformed into (-x, -y, -z).
To regain symmetry, the parity operator must be combined
with charge conjugation (C), which converts particles
into antiparticles. However, this combined operation
called CP is still violated 0.2-0.3% of the time.
Some have compared looking for it like someone waving
in a mirror 1000 times. 997 times the proper hand
waves back, but 3 times the wrong hand does!
This asymmetry in nature allows a distinction between matter
and antimatter and may be responsible for the dominance of matter.
Translation, [Translation] Vector, Magnitude
A composition of two (or any even numbered) reflections over parallel lines
will result in a translation. This is also termed a slide
because it looks like the original image slid from one location to another.
If S is our first transformation, P is our point,
and T is our second transformation, we represent
this composition either as T(S(P)) or T°S(P).
The distance between the parallel lines determines the
distance moved, or the distance from any point on the
preimage to its corresponding image point.
Specifically, the magnitude of a translation is twice the
distance between the parallel lines used to reflect the image.
|
The direction of the slide is given by a vector
from any preimage point to its corresponding image point.
|
A vector is an entity that has both magnitude and direction.
|
(Note: our textbooks calls vector a quantity but few use this term to
specify the subject of a mathematical operation. Even fewer would
call the Riemann Curvature Tensor a quantity!)
Magnitude or modulus is the length of a vector.
Symbolically it is specified as: |v|.
Although the same symbol is used, THIS IS NOT absolute value
(some unfortunately may disagree). However, the result is also a nonnegative real number.
Sadly, many textbooks introduce this confusion and our TI-84+ calculators
propagate it by use of abs to find vector magnitudes.
Note: non-real complex numbers are neither positive nor negative and thus
you cannot find their absolute value. However, you can find their distance
from the origin (magnitude).
Direction can often be specified using a
clock (12 o'clock is straight ahead, 3 o'clock is to your right)
or compass (north is 0°, east is 90°).
Since vectors are often used in conjunction with the
Cartesian Coordinate system, they are often specified using ordered pairs.
Vectors have a head (ending at the image point) and a
tail (located at the corresponding preimage point).
These vector ends are more technically termed: initial point
and terminal point.
The same vector (magnitude and direction) specifies how any
point in the image gets translated, hence the term translation vector.
A vector maintains both its magnitude and its direction as it gets translated
about. When an ordered pair is used to specify a vector, it is assumed
that the ordered pair is the head and the origin the tail.
It may be easy to confuse a vector with a ray.
However, rays are infinite in extent.
Similar notation, two points with a arrow atop can use for both.
However, vectors are often noted using an arrow over a single
lower-case letter or the same letter bolded: v.
A rotation can be generated by reflecting
an image twice over intersecting lines.
The magnitude of the rotation is twice the measure
of the acute angle formed by the intersecting lines.
|
The center of rotation is determined by the point of intersection
of the two lines. Another name for a rotation would be a turn.
Typically one would rotate an image as follows.
1) Reflect the preimage over line one and label the corresponding
image points with a single quote or apostrophe (read as prime).
2) Reflect the image over line two and label the corresponding points
with a double quote (read as double prime).
Your final image should be directly congruent with the original image.
Remember that clockwise rotations are specified as negative,
whereas anticlockwise rotations are specified as positive.
A glide reflection is a composition of a translation and a
reflection where the translation vector is parallel to the line of symmetry.
A glide reflection is also informally termed a walk.
Thus reflections over some combinations of three lines generate a walk.
Since two lines are either parallel or intersect, the resulting
transformed image is either a translation or a rotation.
With three lines the results are more complicated.
Three lines can intersect in zero, one, two, or three points.
(Two might not be obvious until you realize two lines are parallel.)
If three coplanar lines intersect in zero points they are also parallel
and any reflection over all three can be reduced to a single reflection.
If three (or more) coplanar lines intersect in one point, they are termed
concurrent. A reflection over three concurrent
lines can likewise be reduced to a single reflection.
When the composition of reflections over three lines is not equivalent
to a single reflection, the resulting transformation is a glide reflection.
|
A glide reflection can be broken down into a translation and a reflection.
Order isn't critical here, the same image will result whichever is done
first.
These four isometries: reflection, translation, rotation,
and glide reflection are all there are.
Translation, rotation, and glide reflection can all be broken
down into a sequence of reflections. We thus see that reflections
form the basis of all our isometries.
Translation and rotation are the composition of two reflections
and thus preserve orientation, whereas reflection and glide reflection
are the composition of an odd number of reflections and thus
reverse orientation.
Noncongruent or nonisometric transformations are by far the ones more
commonly encountered. The transformation y=2x dilates
(expands or stretches) a figure, whereas the
transformation y=x/2 contracts (shrinks) a figure.
Other transformations such as y=x2
will distort figures in various ways
including bending (shearing) and breaking them.
These will be discussed further in later lessons.
Reflections commonly occur in nature.
Unless there is spin involved the following applies.
|
The angle of incidence is equal to the angle of reflection.
|
The phrase above is commonly learned in physics, but is rooted in
the principles discussed above. It can also be applied in a fun way
on the miniature golf course or billiards (pool) table.
Traditionally these angles are measured from the surface normal
(perpendicular to the reflecting wall) and not from the wall itself,
but this fine point only becomes important later in physics/optics,
when index of refraction, Snell's law, total internal reflection,
and Brewster's angle (for polarization) are introduced.
Again, spin must be zero so energy is not being exchanged
due to conversion between linear and angular momentum. We often also
assume no friction so energy is conserved. Noether's Theorem, derived by
Emmy Noether,
one of the few great female mathematicians, tells us there is
a correspondance between symmetry and conservation laws.
Sketched below left is a typical miniature golf set up requiring reflections.
Ball A is to be hit so that it will go in hole B.
Below right we have reflected hole B against the bottom wall to
produce B'. We have reflected B' against the top wall to
produce B". Ball A is then struck toward B".
When it hits the top wall it reflects toward B'.
When it hits the bottom wall it reflects toward B—a hole-in-one!
A good exercise for the reader is to verify that there are no one-bounce
holes-in-one possible and that this is the only two bounce hole-in-one possible.
In making miniture golf holes you might consider how to either make the
ball bounce away or toward the hole. A concept similar to bouncing
the ball ever toward the hole is a
whispering gallery,
a term now taken over by
chat groups, rock bands, and laser modes.
In addition to the constructions
listed
in the last lesson, the following should be
mastered
by the time the student finishes this lesson.
In addition, the student will be exposed
to the construction of a regular pentagon.
- Construct a perpendicular to a line at a point.
- Construct a regular quadrilateral (square).
- Construct a regular octagon.
- Construct a perpendicular to a line through a given point not on the line.
- Construct a parallel to a line through a point (not on the line) (three methods).
To construct a perpendicular to a line at a point, select an arbitrary
distance with your compass and mark points on the line on either side
of the point at that distance. Now set the compass slightly larger and
proceed as you would to find the perpendicular bisector.
The construction of a perpendicular to a line through a given point
is similar. The compass still starts on the point, but the point is
no longer on the line.
To construct a regular quadrilateral start with a line segment more than twice as
long as the desired quadrilateral. Locate points A and B approximately
centered within your segment as two corners of the quadrilateral.
Construct perpendiculars through both A and B. On the same side of
line AB, mark the distance AB off on each perpendicular. Call these
points C and D, preferrably with C associated with the perpendicular
through B. If C and D are connected, you should have a square.
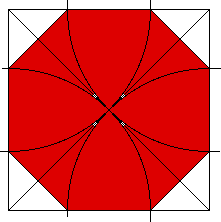 The construction of the octagon is a little trickier. Construct a square.
Locate the square's center using diagonals.
Set the compass to the distance from a corner to the center.
Draw arcs intersecting two sides from each corner.
Connect these intersection points in sequence.
Proof of this method and another method are given
here.
An alternate method, perhaps more straight-forward, is to circumscribe
a square, bisects the sides, and connect the points of intersection
between the square's vertices, the bisectors, and the circle.
The construction of the octagon is a little trickier. Construct a square.
Locate the square's center using diagonals.
Set the compass to the distance from a corner to the center.
Draw arcs intersecting two sides from each corner.
Connect these intersection points in sequence.
Proof of this method and another method are given
here.
An alternate method, perhaps more straight-forward, is to circumscribe
a square, bisects the sides, and connect the points of intersection
between the square's vertices, the bisectors, and the circle.
One of my favorite problems is finding the exact area of an octagon.
It nicely combines working with radicals and binomials.
Let the octagon's sides be 2.
We can find the area by subtracting the area of the four triangles
from the area of the bounding square.
The area of the square is (2+2x)2, where x
is the side an isosceles right triangle with hypotenuse of 2.
Using the Pythagorean theorem we obtain
x2+x2=22 or
2x2=4 or x2=2 or
x=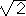 (where we can safely ignore
the negative root since it is a distance).
Thus the square's area is(2+2
(where we can safely ignore
the negative root since it is a distance).
Thus the square's area is(2+2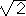 )2=
4(1+
)2=
4(1+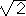 )2=4(1+2
)2=4(1+2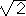 +2)=
8(1+
+2)=
8(1+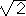 )+4.
The four triangles are 4(½x2)=4.
(This can also be seen by putting the four
triangles together into a square with side of 2.)
Thus our final answer is 8(1+
)+4.
The four triangles are 4(½x2)=4.
(This can also be seen by putting the four
triangles together into a square with side of 2.)
Thus our final answer is 8(1+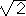 ).
).
Construct a perpendicular to a line through a given point not on the line.
To construct a perpendicular to a line through a given point
not on the line, set the compass some distance greater than the
distance of the point from the line and mark two small arcs
intersecting the line at that distance. Now from each of these
points, locate a point equidistant from these two points
where this equidistance is rather arbitrary. This new point,
and the given point, both line on a perpendicular so join and
extend them.
There are three main methods of constructing a parallel to a line through
a point (P) not on the line. One is known as the equidistant method,
another the rhombus method, and the third as
two perpendiculars.
The equidistant method uses a perpendicular through the point
not on the line and an additional perpendicular most anywhere (the further
away the better). The distance from point P to the line is transferred
to the other perpendicular and used to construct the parallel.
A rhombus is a quadrilateral with all sides equal. This last fact
means that it is also a parallelogram. Proceed by drawing any
line through P intersecting the line at Q. Now from point Q
draw an arc through P and intersecting the given line at R.
Locate the point S the distance PQ
from P and R by drawing small arcs.
Students have the least difficulty with the two perpendiculars
method so we will keep this discussion short.
Once a perpendicular is constructed through the point not on the
line, then a perpendicular to that perpendicular is constructed
at the given point.
The activity
for this section details the construction of the regular pentagon.
Although the regular heptagon was listed as unconstructable, the
regular heptadecagon (17-gon) is constructible as are any n-gons
where n has only factors of 2m,
primes (possibly more than one, but all different)
of the form 22n+1. The 32 known
constructible
n-gons for odd n can found by using Pascal's
Triangle down to row 32 and treating as binary odd=1 and even=0.
Unless another prime Fermat number
is found, this is all there are.
Now that we have the diagonal equation for finding the number of
diagonals for a given n-gon, we can invert the process,
start with the number of diagonals and find the number of sides,
to practice using the quadratic formula.
Consider an n-gon with 119 diagonals.
Because of my fondness for the heptadecagon, some might quickly guess
n = 17 and be correct.
However, we want a way to solve this kind of problem in general.
First, observe 119 = n(n-3)/2. Vertically under this
distribute the 2: 238 = n2 - 3n and then
n2 - 3n - 238 = 0.
In general there are three
main ways to solve such an equation and find the roots, zeroes,
solutions, or x-intercepts. These three methods are
factoring, graphing, and using the quadratic formula.
Not all quadratics factor and some students spend six weeks in
algebra trying to learn the method. I choose not to formally
teach factoring, relating instead the roots to the factors.
Thus, this factors into (n-17)(n+14) = 0 and if a product
equals zero, one of its factors must be zero, so
(n-17) = 0 or (n+14) = 0 or
n ![[is in]](in.gif) {17,-14}.
Since n-gons have three or more sides, we can reject the
extraneous, negative root. Notice how the solution 17 relates to
the factor (n-17), specifically, being the number which make
(n-17) = 0. This concept is useful for constructing factors
from zeroes when graphs (or tables) are used.
{17,-14}.
Since n-gons have three or more sides, we can reject the
extraneous, negative root. Notice how the solution 17 relates to
the factor (n-17), specifically, being the number which make
(n-17) = 0. This concept is useful for constructing factors
from zeroes when graphs (or tables) are used.
The multiplication property of zero was used above.
Formally we may state: x = 0 or y = 0 if and only if xy = 0.
Less formally we can say if a product is zero, one if its factors is zero.
For more information on the graphing calculator see
Numbers Activity 11.
For more information on the quadratic formula see
Numbers Lesson 12.
 The alternative is to adopt something like SAS triangle
congruence (see chapter 7) as an axiom.
Either will be at the heart of a proof of the Isosceles
Triangle Theorem (then base angles are equal) or its converse
(then sides are equal) known as Pons Asinorum,
which
is
Latin for bridge of fools (or asses). This term has come to
mean any problem which severely tests the ability of an
inexperienced person.
The alternative is to adopt something like SAS triangle
congruence (see chapter 7) as an axiom.
Either will be at the heart of a proof of the Isosceles
Triangle Theorem (then base angles are equal) or its converse
(then sides are equal) known as Pons Asinorum,
which
is
Latin for bridge of fools (or asses). This term has come to
mean any problem which severely tests the ability of an
inexperienced person.![[image of a miniature golf hole]](mgolf1.jpg)
![[image of a ball path bouncing twice into a miniature golf hole]](mgolf2.jpg)
 The construction of the octagon is a little trickier. Construct a square.
Locate the square's center using diagonals.
Set the compass to the distance from a corner to the center.
Draw arcs intersecting two sides from each corner.
Connect these intersection points in sequence.
Proof of this method and another method are given
The construction of the octagon is a little trickier. Construct a square.
Locate the square's center using diagonals.
Set the compass to the distance from a corner to the center.
Draw arcs intersecting two sides from each corner.
Connect these intersection points in sequence.
Proof of this method and another method are given
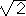 (where we can safely ignore
the negative root since it is a distance).
Thus the square's area is(2+2
(where we can safely ignore
the negative root since it is a distance).
Thus the square's area is(2+2