Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
The King will reply, ‘Truly I tell you, whatever you did for one of the least of these brothers and sisters of mine, you did for me.’ Matthew 25:40 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.6.2
The average cost of a dozen eggs from a small farm can be modeled by \(C(x) = \frac{0.364x+5790}{x}\), where x is the number of eggs produced in dozens. The farmer would like to keep the costs less than $0.75 per dozen eggs. How many eggs would his chickens have to produce?
This function is not linear and the solution will be an interval of answers since there is a range for the desired costs. The words "less than" indicate an inequality. Thus, the function is an example of a nonlinear inequality.
A nonlinear inequality is a mathematical statement containing an inequality such as < or > and the expression does not describe a straight line.
The first step to solve a nonlinear inequality is to find the critical numbers. These are input values that make the expression equal zero or be undefined.
The average cost of a dozen eggs from a small farm can be modeled by \(C(x) = \frac{0.364x+5790}{x}\), where x is the number of eggs produced in dozens. The farmer would like to keep the costs less than $0.75 per dozen eggs. How many eggs would his chickens have to produce?
Solution
Write the inequality based on the problem. The costs are to be less than $0.75, so the 0.75 is the biggest the costs can be. So, the big side of the inequality will face the 0.75.
$$ 0.75 > \frac{0.364x+5790}{x} $$
Make one side zero and simplify.
$$ 0 > \frac{0.364x+5790}{x} - 0.75 $$
$$ 0 > \frac{0.364x+5790}{x} - \frac{0.75x}{x} $$
$$ 0 > \frac{-0.386x+5790}{x} $$
Find the zeros by replacing the inequality with an equal sign and solve for x.
$$ 0 = \frac{-0.386x+5790}{x} $$
0 = -0.386x + 5790
−5790 = −0.386x
x = 15,000
Find any x-values that cause the expression to be undefined.
$$ 0 > \frac{-0.386x+5790}{x} $$
The function will be undefined if the denominator is equal to zero. So, x = 0 is a critical number.
The critical numbers are 0 and 15,000.
Find the critical numbers of 0 < 2x2 − 9x − 5.
Answer
−1⁄2, 5
Now that we have found the critical numbers, we can finish solving for x. The critical numbers are places where the function can change from the positive numbers to negative. In other words, the critical numbers show where the function changes between greater than zero and less than zero. If we test the intervals between the critical numbers, we can see which are greater than zero and which are less than zero.
The average cost of a dozen eggs from a small farm can be modeled by \(C(x) = \frac{0.364x+5790}{x}\), where x is the number of eggs produced in dozens. The farmer would like to keep the costs less than $0.75 per dozen eggs. How many eggs would his chickens have to produce?
Solution
This was already rewritten in example 1 as
$$ 0 > \frac{-0.386x+5790}{x} $$
and the critical numbers are 0 and 15,000.
Plot those critical numbers on a number line.
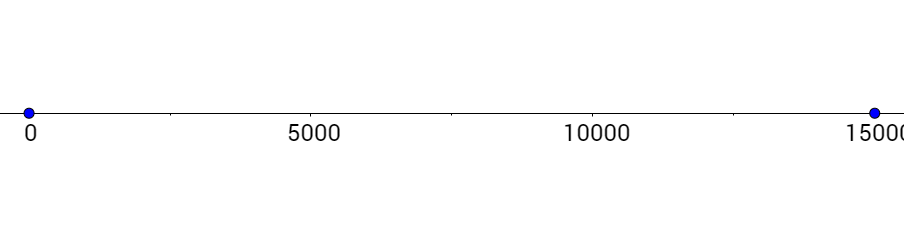
Choose a number in each interval between the critical numbers. −100, 5000, and 15100 will work.
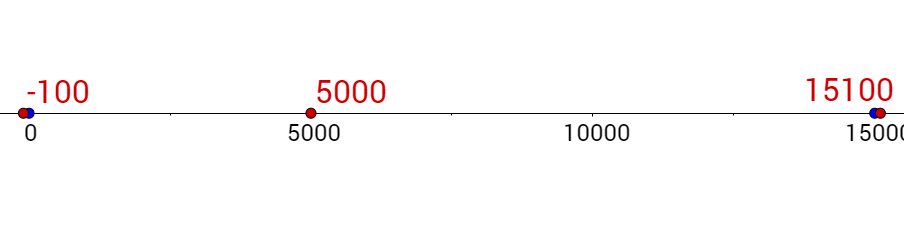
Test these in the inequality to see which produce true statements.
$$ -100: 0 > \frac{-0.386(-100)+5790}{-100} \rightarrow 0 > -58.286 \text{ True} $$
$$ 5000: 0 > \frac{-0.386(5000)+5790}{5000} \rightarrow 0 > 0.772 \text{ False} $$
$$ 15100: 0 > \frac{-0.386(15100)+5790}{15100} \rightarrow 0 > -0.00256 \text{ True} $$
The solutions are the true intervals: (−∞, 0) and (15,000, ∞). Since the hens cannot produce a negative number of eggs, the farm needs to produce more than 15,000 dozen eggs.
Analysis
Both ends of the intervals are parentheses because the inequality is not an equals inequality. If the inequality was ≤ or ≥, there would be a bracket at the end of the interval. However, critical numbers that cause the expression to be undefined always are given a parenthesis in interval notation because x cannot be those numbers.
Solve \(-2 ≤ \frac{2x^2-12}{x}\).
Solution
Solve one side for zero.
$$ 0 ≤ \frac{2x^2-12}{x} + 2 $$
$$ 0 ≤ \frac{2x^2-12}{x} + \frac{2x}{x} $$
$$ 0 ≤ \frac{2x^2+2x-12}{x} $$
Find the critical numbers.
$$ 0 = \frac{2x^2+2x-12}{x} $$
0 = 2x2 + 2x − 12
0 = 2(x2 + x − 6)
0 = 2(x + 3)(x − 2)
x = −3, 2
0 is also a critical number because the inequality is undefined when x = 0.
Graph the critical numbers on a number line and pick test numbers in each interval. −4, −1, 1 and 3 will work for test numbers.
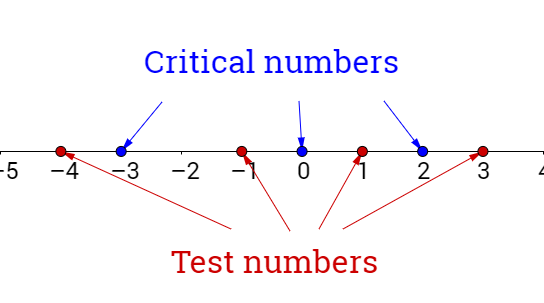
Test the test numbers in the solved inequality.
$$ -4: 0 ≤ \frac{2(-4)^2+2(-4)-12}{(-4)} \rightarrow 0 ≤ -3 \text{ False} $$
$$ -1: 0 ≤ \frac{2(-1)^2+2(-1)-12}{(-1)} \rightarrow 0 ≤ 12 \text{ True} $$
$$ 1: 0 ≤ \frac{2(1)^2+2(1)-12}{(1)} \rightarrow 0 ≤ -8 \text{ False} $$
$$ 3: 0 ≤ \frac{2(3)^2+2(3)-12}{(3)} \rightarrow 0 ≤ 4 \text{ True} $$
The solutions are [−3, 0) and [2, ∞).
Analysis
The critical number 0 comes from when the inequality is undefined, so x ≠ 0. That is why the 0 has a parenthesis by it. The −3 and 2 have brackets by them because x can equal them from the ≤ sign.
Solve 0 < 2x2 − 9x − 5.
Answer
(−1⁄2, 5)
An alternative way to solve nonlinear inequalities is by graphing. Remember a coordinate plane is simply two number lines set perpendicularly. By solving the inequality so that one side is zero and graphing the expression, the function can be compared with zero. The critical numbers are the zeros and the undefined values. The zeros occur at the x-intercepts; the undefined values often occur at vertical asymptotes. These can both be read from the graph. Intervals on the graph where the y-values are positive are where the inequality is greater than zero. Negative y-values show the intervals where the inequality is less than zero.
Solve 8 ≥ x2 − 2x.
Solution
Solve the inequality so one side is zero.
8 ≥ x2 − 2x
0 ≥ x2 − 2x − 8
Graph the right-hand expression.
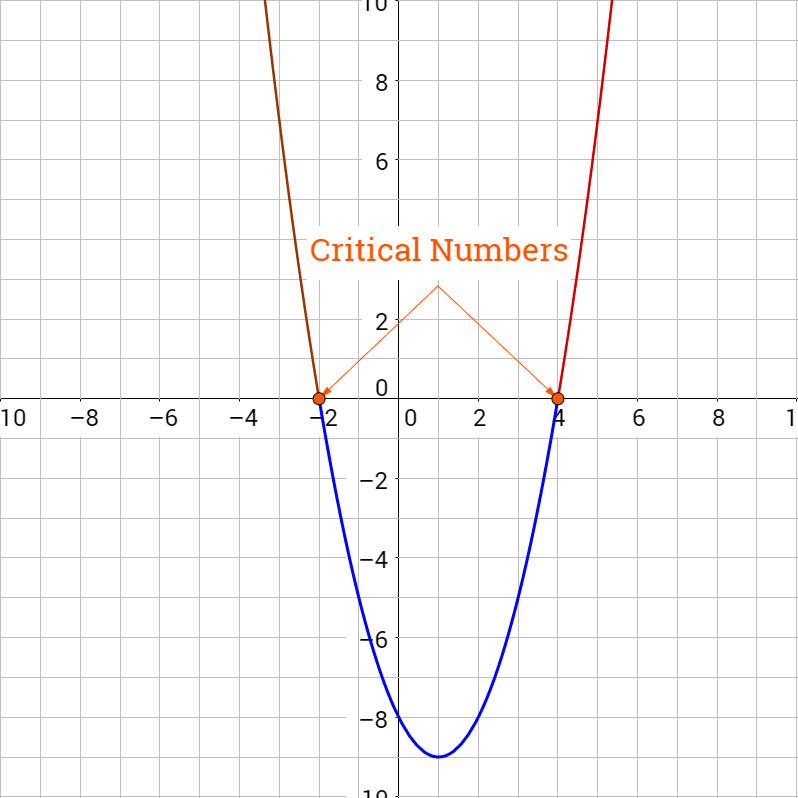
Since the expression is less than zero, the solutions are intervals with negative y-values. The solution is [−2, 4].
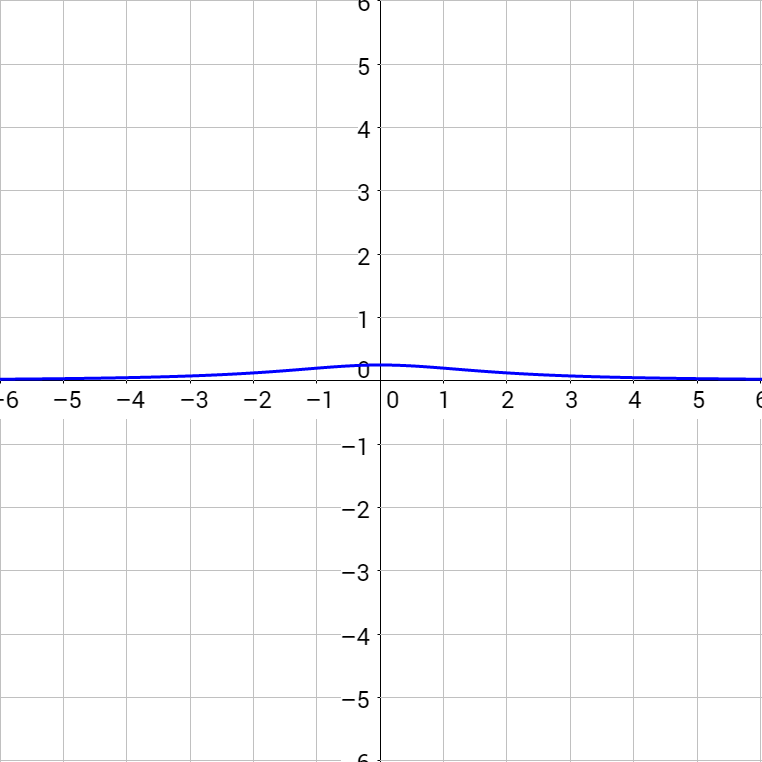
Solve \(0 < \frac{x-3}{x^2+x-2}\).
Solution
The inequality is already solved for zero, so graph the right-hand expression.
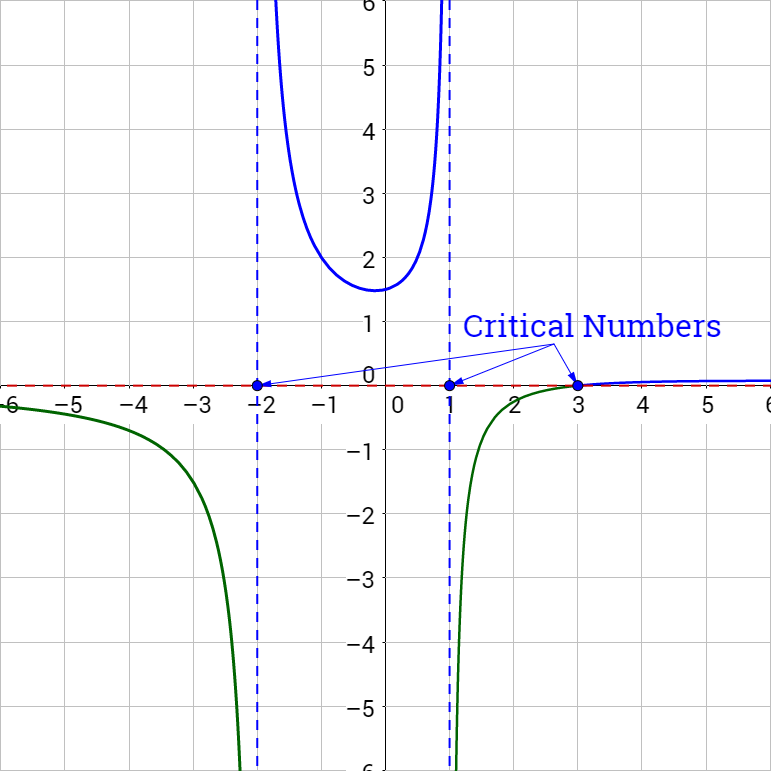
Since the expression is greater than zero, the solutions are intervals with positive y-values. The solutions are (−2, 1) ∪ (3, ∞).
Solve \(0 > \frac{x^2}{x-2}\) by graphing.
Answer
(2, ∞)
A nonlinear inequality is a mathematical statement containing an inequality such as < or > and the expression does not describe a straight line.
Helpful videos about this lesson.
