5-06 Multiple Angle Formulas

Evaluate Trigonometric Functions

A roof is planned with a steepness of 3/12 meaning that the angle formed with horizontal is \(\tan θ = \frac{3}{12}\). To make snow slide off easier, the designer wants to double the angle of the roof. a) What would be the new steepness? b) Also find sin 2θ and c) cos 2θ.

Solution

1. By steepness, the problem is asking for what is tan 2θ? Use the double-angle formula for tangent.

   $$\tan 2θ = \frac{2 \tan θ}{1 - \tan^2 θ}$$

   $$= \frac{2\left(\frac{3}{12}\right)}{1 - \left(\frac{3}{12}\right)^2}$$

   $$= \frac{2\left(\frac{1}{4}\right)}{1 - \left(\frac{1}{4}\right)^2}$$

   $$= \frac{\frac{1}{2}}{1 - \frac{1}{16}}$$

   $$= \frac{\frac{1}{2}}{\frac{15}{16}}$$

   $$= \frac{1}{2} ⋅ \frac{16}{15}$$

   $$= \frac{8}{15}$$

2. Tangent gives the ratio opposite/adjacent in right triangles. Draw the triangle and use the Pythagorean theorem to find the hypotenuse.

   

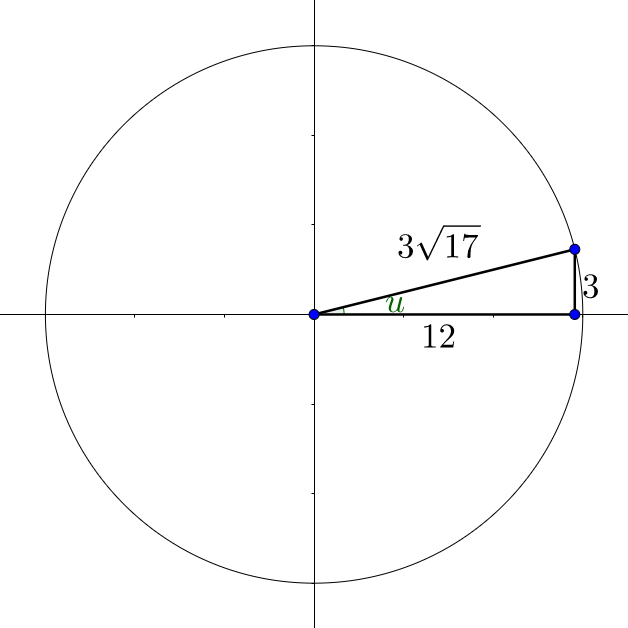
   a² + b² = c²

   12² + 3² = hyp²

   153 = hyp²

   $$hyp = 3\sqrt{17}$$

   So \(\sin θ = \frac{3}{3\sqrt{17}} = \frac{\sqrt{17}}{17}\) and \(\cos θ = \frac{12}{3\sqrt{17}} = \frac{4\sqrt{17}}{17}\). Now use the double angle formula for sine.

   sin 2θ = 2 sin θ cos θ

   $$= 2\left(\frac{\sqrt{17}}{17}\right)\left(\frac{4\sqrt{17}}{17}\right)$$

   $$= \frac{136}{289} = \frac{8}{17}$$

3. Cosine has three options for the double-angle formula. Choose one that is convenient.

   cos 2θ = 2 cos² θ − 1

   $$= 2 \left(\frac{4\sqrt{17}}{17}\right)^2 - 1$$

   $$= 2 \left(\frac{16}{17}\right) - 1$$

   $$= \frac{32}{17} - 1$$

   $$= \frac{15}{17}$$

Solve a Trigonometric Equation

Find all solutions on the interval [0, 2π) of sin x + sin 2x = 0.

Solution

Start by using the double-angle formula for sine.

sin x + 2 sin x cos x = 0

Factor out sin x.

sin x (1 + 2 cos x) = 0

Set each factor equal to zero and solve.

sin x = 0	1 + 2 cos x = 0
	\(\cos x = -\frac{1}{2}\)
x = 0, π	\(x = \frac{2π}{3}, \frac{4π}{3}\)

Derive a New Identity

Derive a triple-angle formula for sin 3x.

Solution

Start by rewriting the sin 3x as sin (2x + x) so a sum formula can be used.

sin 3x = sin (2x + x)

= sin 2x cos x + cos 2x sin x

Use double-angle formulas.

= (2 sin x cos x)cos x + (2 cos² x − 1)sin x

Multiply and distribute.

= 2 sin x cos² x + 2 sin x cos² x − sin x

Combine like terms.

= 4 sin x cos² x − sin x

Use a Pythagorean identity to change cos² x to 1 − sin² x so that only sine is used.

= 4 sin x (1 − sin² x) − sin x

Distribute.

= 4 sin x − 4 sin³ x − sin x

= 3 sin x − 4 sin³ x

Derive a Power-Reducing Formula of Higher Degree

Rewrite sin⁴ x as a sum of 1^st powers of cosine.

Solution

Rewrite sin⁴ x in terms of sin² x.

sin⁴ x = sin² x sin² x

Substitute the power-reducing formula for sine.

$$= \left(\frac{1 - \cos 2x}{2}\right)\left(\frac{1 - \cos 2x}{2}\right)$$

Multiply.

$$= \frac{1}{4}\left(1 - 2\cos 2x + \cos^2 2x\right)$$

Since a new squared term resulted, use the power-reducing formula for cosine with u = 2x.

$$= \frac{1}{4}\left(1 - 2\cos 2x + \left(\frac{1 + \cos 2\left(2x\right)}{2}\right)\right)$$

Get a common denominator.

$$= \frac{1}{4}\left(\frac{2}{2} - \frac{4\cos 2x}{2} + \frac{1 + \cos 4x}{2}\right)$$

Multiply the denominator and combine like terms.

$$= \frac{1}{8}\left(3 - 4\cos 2x + \cos 4x\right)$$

Evaluate a Trigonometric Function

Find the exact value of sin 165°.

Solution

Notice that \(165° = \frac{330°}{2}\), a half-angle formula can be used with u = 330°.

$$\sin 165° = \sin \frac{330°}{2}$$

$$= ±\sqrt{\frac{1 - \cos 330°}{2}}$$

$$= ±\sqrt{\frac{1 - \frac{\sqrt{3}}{2}}{2}}$$

$$= ±\sqrt{\frac{\frac{2}{2} - \frac{\sqrt{3}}{2}}{2}}$$

$$= ±\sqrt{\frac{\frac{2 - \sqrt{3}}{2}}{2}}$$

$$= ±\sqrt{\frac{2 - \sqrt{3}}{4}}$$

$$= ±\frac{\sqrt{2 - \sqrt{3}}}{2}$$

Because 165° is in quadrant II and sine is positive in quadrant II, only the + should be used from the ±.

$$\sin 165° = \frac{\sqrt{2 - \sqrt{3}}}{2}$$

Solve a Trigonometric Equation

Find all the solutions of \(\cos x = 2 \sin^2 \frac{x}{2}\).

Solution

The quickest way to solve this equation is to use a half-angle formula for \(\sin \frac{x}{2}\). The square on this term will cancel the square root in the half-angle formula.

$$\cos x = 2 \sin^2 \frac{x}{2}$$

$$\cos x = 2 \left(±\sqrt{\frac{1 - \cos x}{2}}\right)^2$$

$$\cos x = 2\left(\frac{1 - \cos x}{2}\right)$$

$$\cos x = 1 - \cos x$$

$$2 \cos x = 1$$

$$\cos x = \frac{1}{2}$$

$$x = \frac{2π}{3} + 2πn, \frac{5π}{3} + 2πn$$