Precalculus by Richard Wright
Precalculus by Richard Wright
For the Lord your God is a merciful God; he will not abandon or destroy you or forget the covenant with your ancestors, which he confirmed to them by oath. Deuteronomy 4:31 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.6.4, PC.6.6

Even though Gaussian Elimination was not discovered by Gauss, his notation was used in Europe. In 1888, Wilhelm Jordan discovered a way to extend Gaussian Elimination, so mathematicians have named the process Gauss-Jordan Elimination. Gauss-Jordan Elimination involves using elementary row operations to write a system or equations, or matrix, in reduced-row echelon form. Reduced-row echelon form is like row echelon form, except that every element above and below and leading 1 is a 0.
A matrix is in reduced row-echelon form when
The following matrices are in reduced row-echelon form.
$$ \left[\begin{matrix} 1 & 0 & 2 \\ 0 & 1 & 3 \\ 0 & 0 & 0 \end{matrix}\right] \qquad \left[\begin{matrix} 1 & 2 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}\right] $$
Are the following matrices in reduced-row echelon form?
Solution
Are the following matrices in reduced-row echelon form?
Answers
Use Gauss-Jordan Elimination to put the matrix in reduced-row echelon form.
$$ \left[\begin{matrix} 1 & 2 & -2 & -6 \\ 2 & 1 & 0 & 3 \\ -1 & 3 & 3 & 4 \end{matrix}\right] $$
Solution
There are no zeros in the first column, so there is no need to switch any of the rows around. Start by working down the 1st column by getting rid of the 2 in the first column. Multiply the 1st row by −2 and add to 2nd row.
When showing your work on your assignment, you typically only show the steps with the red numbers in them.
$$ \begin{matrix} \swarrow ×\left(-2\right) \\ +\rightarrow \qquad \\ \quad \end{matrix} \left[\begin{matrix} 1 & 2 & -2 & -6 \\ \color{blue}{2} & 1 & 0 & 3 \\ -1 & 3 & 3 & 4 \end{matrix}\right] $$
$$ \left[\begin{matrix} 1 & 2 & -2 & -6 \\ \color{red}{0} & \color{red}{-3} & \color{red}{4} & \color{red}{15} \\ -1 & 3 & 3 & 4 \end{matrix}\right] $$
Get rid of the −1 in the 1st column by adding row 1 to row 3.
$$ \begin{matrix} \swarrow \\ \downarrow \quad \\ +\rightarrow \end{matrix} \left[\begin{matrix} 1 & 2 & -2 & -6 \\ 0 & -3 & 4 & 15 \\ \color{blue}{-1} & 3 & 3 & 4 \end{matrix}\right] $$
$$ \left[\begin{matrix} 1 & 2 & -2 & -6 \\ 0 & -3 & 4 & 15 \\ \color{red}{0} & \color{red}{5} & \color{red}{1} & \color{red}{-2} \end{matrix}\right] $$
Now work down the 2nd column. Multiply the 2nd row by 5 and add to 3 times the 3rd row.
$$ \begin{matrix} \quad \\ \swarrow ×5 \\ +\rightarrow ×3 \end{matrix} \left[\begin{matrix} 1 & 2 & -2 & -6 \\ 0 & -3 & 4 & 15 \\ 0 & \color{blue}{5} & 1 & -2 \end{matrix}\right] $$
$$ \left[\begin{matrix} 1 & 2 & -2 & -6 \\ 0 & -3 & 4 & 15 \\ \color{red}{0} & \color{red}{0} & \color{red}{23} & \color{red}{69} \end{matrix}\right] $$
The 3rd row can now be simplified, so multiply by \(\frac{1}{23}\).
$$ \begin{matrix} \quad \\ \quad \\ ×\tfrac{1}{23} \end{matrix} \left[\begin{matrix} 1 & 2 & -2 & -6 \\ 0 & -3 & 4 & 15 \\ 0 & 0 & 23 & 69 \end{matrix}\right] $$
$$ \left[\begin{matrix} 1 & 2 & -2 & -6 \\ 0 & -3 & 4 & 15 \\ \color{red}{0} & \color{red}{0} & \color{red}{1} & \color{red}{3} \end{matrix}\right] $$
The matrix is almost in row echelon form except for the leading nonzero entry in the 2nd row is not 1. If it was turned into a 1, then there would be fractions. However, fractions would make the remaining process a bit more of a nuisance, so it will be left as a −3 for now. It is time to begin the Jordan part of the Gauss-Jordan Elimination. Because there are three rows, start getting zeros in the 3rd column and work from bottom up. Get rid of the 4 in the 2nd row by multiplying the 3rd row by −4 and adding to the 2nd row.
$$ \begin{matrix} \quad \\ +\rightarrow \qquad \\ \nwarrow ×\left(-4\right) \end{matrix} \left[\begin{matrix} 1 & 2 & -2 & -6 \\ 0 & -3 & \color{blue}{4} & 15 \\ 0 & 0 & 1 & 3 \end{matrix}\right] $$
$$ \left[\begin{matrix} 1 & 2 & -2 & -6 \\ \color{red}{0} & \color{red}{-3} & \color{red}{0} & \color{red}{3} \\ 0 & 0 & 1 & 3 \end{matrix}\right] $$
The second row can be simplified, multiply it by \(-\frac{1}{3}\).
$$ \begin{matrix} \quad \\ ×\left(-\tfrac{1}{3}\right) \\ \quad \end{matrix} \left[\begin{matrix} 1 & 2 & -2 & -6 \\ 0 & -3 & 0 & 3 \\ 0 & 0 & 1 & 3 \end{matrix}\right] $$
$$ \left[\begin{matrix} 1 & 2 & -2 & -6 \\ \color{red}{0} & \color{red}{1} & \color{red}{0} & \color{red}{-1} \\ 0 & 0 & 1 & 3 \end{matrix}\right] $$
Continue working up the the 3rd column. Get rid of the −2 in the 1st row by multiplying the 3rd row by 2 and adding to the 1st row.
$$ \begin{matrix} +\rightarrow\quad \\ \uparrow\qquad \\ \nwarrow ×2 \end{matrix} \left[\begin{matrix} 1 & 2 & \color{blue}{-2} & -6 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & 3 \end{matrix}\right] $$
$$ \left[\begin{matrix} \color{red}{1} & \color{red}{2} & \color{red}{0} & \color{red}{0} \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & 3 \end{matrix}\right] $$
Now that the 3rd column is done, move up the 2nd column. Get rid of the 2 in the 1st row by multiplying the 2nd row by −2 and adding to the 1st row.
$$ \begin{matrix} +\rightarrow \qquad \\ \nwarrow ×\left(-2\right) \\ \quad \end{matrix} \left[\begin{matrix} 1 & \color{blue}{2} & 0 & 0 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & 3 \end{matrix}\right] $$
$$ \left[\begin{matrix} \color{red}{1} & \color{red}{0} & \color{red}{0} & \color{red}{2} \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & 3 \end{matrix}\right] $$
The matrix is now in reduced-row echelon form.
Write the matrix in reduced-row echelon form.
$$ \left[\begin{matrix} 1 & 3 & -1 \\ 1 & 4 & -2 \\ -1 & -2 & 2 \end{matrix}\right] $$
Answer
\(\left[\begin{matrix} 1 & 0 & -2 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{matrix}\right]\)
If solving a system of linear equations with Gauss-Jordan Elimination and a row becomes all zeros with
Solve using Gauss-Jordan Elimination
$$ \left\{\begin{align} x + y \qquad &= 0 \\ 2x - y - z &= 5 \\ -3x + 2y + z &= -9 \end{align}\right. $$
Solution
Start by writing the system as a matrix.
$$ \left[\begin{matrix} 1 & 1 & 0 & 0 \\ 2 & -1 & -1 & 5 \\ -3 & 2 & 1 & -9 \end{matrix}\right] $$
Work down the 1st column. Start by getting rid of the 2 in the 2nd row. Multiply the 1st row by −2 and add to 2nd row.
$$ \begin{matrix} \swarrow ×\left(-2\right) \\ +\rightarrow \qquad \\ \quad \end{matrix} \left[\begin{matrix} 1 & 1 & 0 & 0 \\ \color{blue}{2} & -1 & -1 & 5 \\ -3 & 2 & 1 & -9 \end{matrix}\right] $$
$$ \left[\begin{matrix} 1 & 1 & 0 & 0 \\ \color{red}{0} & \color{red}{-3} & \color{red}{-1} & \color{red}{5} \\ -3 & 2 & 1 & -9 \end{matrix}\right] $$
Get rid of the −3 in the 1st column by multiplying the 1st row by 3 and adding it to row 3.
$$ \begin{matrix} \swarrow ×3 \\ \downarrow \quad \\ +\rightarrow \end{matrix} \left[\begin{matrix} 1 & 1 & 0 & 0 \\ 0 & -3 & -1 & 5 \\ \color{blue}{-3} & 2 & 1 & -9 \end{matrix}\right] $$
$$ \left[\begin{matrix} 1 & 1 & 0 & 0 \\ 0 & -3 & -1 & 5 \\ \color{red}{0} & \color{red}{5} & \color{red}{1} & \color{red}{-9} \end{matrix}\right] $$
Now work down the 2nd column. Multiply the 2nd row by 5 and add to 3 times the 3rd row.
$$ \begin{matrix} \quad \\ \swarrow ×5 \\ +\rightarrow ×3 \end{matrix} \left[\begin{matrix} 1 & 1 & 0 & 0 \\ 0 & -3 & -1 & 5 \\ 0 & \color{blue}{5} & 1 & -9 \end{matrix}\right] $$
$$ \left[\begin{matrix} 1 & 1 & 0 & 0 \\ 0 & -3 & -1 & 5 \\ \color{red}{0} & \color{red}{0} & \color{red}{-2} & \color{red}{-2} \end{matrix}\right] $$
The 3rd row can now be simplified, so multiply by \(-\frac{1}{2}\).
$$ \begin{matrix} \quad \\ \quad \\ ×\left(-\tfrac{1}{2}\right) \end{matrix} \left[\begin{matrix} 1 & 1 & 0 & 0 \\ 0 & -3 & -1 & 5 \\ 0 & 0 & -2 & -2 \end{matrix}\right] $$
$$ \left[\begin{matrix} 1 & 1 & 0 & 0 \\ 0 & -3 & -1 & 5 \\ \color{red}{0} & \color{red}{0} & \color{red}{1} & \color{red}{1} \end{matrix}\right] $$
The matrix is almost in row echelon form except for the leading nonzero entry in the 2nd row is not 1. If it was turned into a 1, then there would be fractions. However, fractions would make the remaining process a bit more of a nuisance, so it will be left as a -3 for now. It is time to begin the Jordan part of the Gauss-Jordan Elimination. Because there are three rows, start getting zeros in the 3rd column and work from bottom up. Get rid of the -1 in the 2nd row by adding the 3rd row to the 2nd row.
$$ \begin{matrix} \quad \\ +\rightarrow \quad \\ \nwarrow \end{matrix} \left[\begin{matrix} 1 & 1 & 0 & 0 \\ 0 & -3 & \color{blue}{-1} & 5 \\ 0 & 0 & 1 & 1 \end{matrix}\right] $$
$$ \left[\begin{matrix} 1 & 1 & 0 & 0 \\ \color{red}{0} & \color{red}{-3} & \color{red}{0} & \color{red}{6} \\ 0 & 0 & 1 & 1 \end{matrix}\right] $$
The second row can be simplified, multiply it by \(-\frac{1}{3}\).
$$ \begin{matrix} \quad \\ ×\left(-\tfrac{1}{3}\right) \\ \quad \end{matrix} \left[\begin{matrix} 1 & 1 & 0 & 0 \\ 0 & -3 & 0 & 6 \\ 0 & 0 & 1 & 1 \end{matrix}\right] $$
$$ \left[\begin{matrix} 1 & 1 & 0 & 0 \\ \color{red}{0} & \color{red}{1} & \color{red}{0} & \color{red}{-2} \\ 0 & 0 & 1 & 1 \end{matrix}\right] $$
Continue working up the the 3rd column. But there is already a zero in the 3rd column of row one. Now that the 3rd column is done, move up the 2nd column. Get rid of the 1 in the 1st row by multiplying the 2nd row by −1 and adding to the 1st row.
$$ \begin{matrix} +\rightarrow \qquad \\ \nwarrow ×\left(-1\right) \\ \quad \end{matrix} \left[\begin{matrix} 1 & \color{blue}{1} & 0 & 0 \\ 0 & 1 & 0 & -2 \\ 0 & 0 & 1 & 1 \end{matrix}\right] $$
$$ \left[\begin{matrix} \color{red}{1} & \color{red}{0} & \color{red}{0} & \color{red}{2} \\ 0 & 1 & 0 & -2 \\ 0 & 0 & 1 & 1 \end{matrix}\right] $$
The matrix is now in reduced-row echelon form. Remember that each row is an equation. The first row says x = 2. The second row says y = −2. And the third row says z = 1. Thus, the solution is (2, −2, 1) which also happens to be the 4th column.
Solve using Gauss-Jordan Elimination
$$ \left\{\begin{align} 2x + y -5z &= 5 \\ y + 2z &= -1 \\ x + 3y - z &= 0 \end{align}\right. $$
Answer
(3, −1, 0)
Solve using Gauss-Jordan Elimination
$$ \left\{\begin{align} 3x + y + z &= 10 \\ x + 2y - 3z &= 10 \\ x + y - z &= 6 \end{align}\right. $$
Solution
Start by writing the system as a matrix.
$$ \left[\begin{matrix} 3 & 1 & 1 & 10 \\ 1 & 2 & -3 & 10 \\ 1 & 1 & -1 & 6 \end{matrix}\right] $$
It would be nice to have a 1 in the top left entry, so switch rows 1 and 2.
$$ \left[\begin{matrix} 1 & 2 & -3 & 10 \\ 3 & 1 & 1 & 10 \\ 1 & 1 & -1 & 6 \end{matrix}\right] $$
Work down the 1st column. Start by getting rid of the 3 in the 2nd row. Multiply the 1st row by −3 and add to 2nd row.
$$ \begin{matrix} \swarrow ×\left(-3\right) \\ +\rightarrow \qquad \\ \quad \end{matrix} \left[\begin{matrix} 1 & 2 & -3 & 10 \\ \color{blue}{3} & 1 & 1 & 10 \\ 1 & 1 & -1 & 6 \end{matrix}\right] $$
$$ \left[\begin{matrix} 1 & 2 & -3 & 10 \\ \color{red}{0} & \color{red}{-5} & \color{red}{10} & \color{red}{-20} \\ 1 & 1 & -1 & 6 \end{matrix}\right] $$
Notice the 2nd row can be simplified by multiplying by \(-\frac{1}{5}\).
$$ \begin{matrix} \quad \\ ×\left(-\tfrac{1}{5}\right) \\ \quad \end{matrix} \left[\begin{matrix} 1 & 2 & -3 & 10 \\ 0 & -5 & 10 & -20 \\ 1 & 1 & -1 & 6 \end{matrix}\right] $$
$$ \left[\begin{matrix} 1 & 2 & -3 & 10 \\ \color{red}{0} & \color{red}{1} & \color{red}{-2} & \color{red}{4} \\ 1 & 1 & -1 & 6 \end{matrix}\right] $$
Get rid of the 1 in the 1st column by multiplying the 1st row by −1 and adding it to row 3.
$$ \begin{matrix} \swarrow ×\left(-1\right) \\ \downarrow \qquad \\ +\rightarrow \quad \end{matrix} \left[\begin{matrix} 1 & 2 & -3 & 10 \\ 0 & 1 & -2 & 4 \\ \color{blue}{1} & 1 & -1 & 6 \end{matrix}\right] $$
$$ \left[\begin{matrix} 1 & 2 & -3 & 10 \\ 0 & 1 & -2 & 4 \\ \color{red}{0} & \color{red}{-1} & \color{red}{2} & \color{red}{-4} \end{matrix}\right] $$
Now work down the 2nd column. Get rid of the −1 in the 3rd row by adding the 2nd row to the 3rd row.
$$ \begin{matrix} \quad \\ \swarrow \\ +\rightarrow \end{matrix} \left[\begin{matrix} 1 & 2 & -3 & 10 \\ 0 & 1 & -2 & 4 \\ 0 & \color{blue}{-1} & 2 & -4 \end{matrix}\right] $$
$$ \left[\begin{matrix} 1 & 2 & -3 & 10 \\ 0 & 1 & -2 & 4 \\ \color{red}{0} & \color{red}{0} & \color{red}{0} & \color{red}{0} \end{matrix}\right] $$
The 3rd row is now all zeros which means many solutions. Still finish putting the matrix in reduced-row echelon form.
It is time to begin the Jordan part of the Gauss-Jordan Elimination. Because the 2nd column has the only leading zero with a nonzero entry above it, get rid of that entry. Get rid of the 2 in the 1st row by adding the −2 times the 2nd row to the 1st row.
$$ \begin{matrix} +\rightarrow \qquad \\ \nwarrow ×\left(-2\right) \\ \quad \end{matrix} \left[\begin{matrix} 1 & \color{blue}{2} & -3 & 10 \\ 0 & 1 & -2 & 4 \\ 0 & 0 & 0 & 0 \end{matrix}\right] $$
$$ \left[\begin{matrix} \color{red}{1} & \color{red}{0} & \color{red}{1} & \color{red}{2} \\ 0 & 1 & -2 & 4 \\ 0 & 0 & 0 & 0 \end{matrix}\right] $$
The matrix is now in reduced-row echelon form.
Remember that each row is an equation.
Because there are no fractions in the coefficients of z, it would be convenient to say
z = a
The second row says y − 2z = 4, so
y = 2a + 4
The first row says x + z = 2. So it becomes
x = −a + 2
Thus, the solution is (−a + 2, 2a + 4, a).
Solve using Gauss-Jordan Elimination
$$ \left\{\begin{align} x + 2y + 5z &= 1 \\ 3x - y - 2z &= 7 \\ 2x - 3y - 7z &= 8 \end{align}\right. $$
Answer
No solution
Most graphing calculators are able to work with matrices. They can add, subtract, and multiply matrices. The graphing calculators can even put matrices into reduced-row echelon form.
TI-84
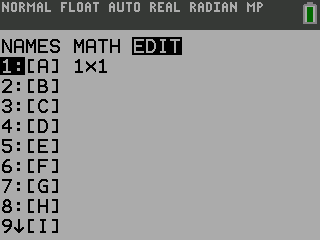
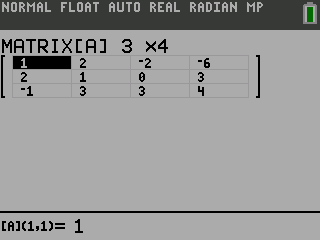
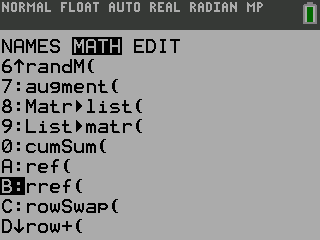
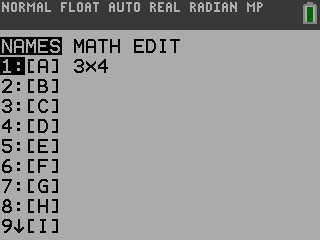
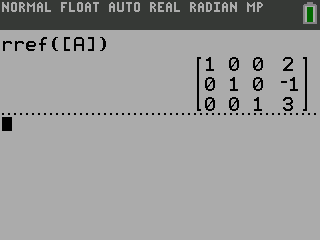
NumWorks
It is faster on the NumWorks to just type in the commands instead of going through menus.


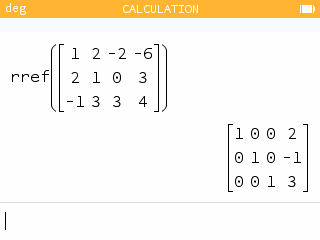
Or this can be done by using the menus, but it takes longer.
A matrix is in reduced row-echelon form when
The following matrices are in reduced row-echelon form.
$$ \left[\begin{matrix} 1 & 0 & 2 \\ 0 & 1 & 3 \\ 0 & 0 & 0 \end{matrix}\right] \qquad \left[\begin{matrix} 1 & 2 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}\right] $$
If solving a system of linear equations with Gauss-Jordan Elimination and a row becomes all zeros with
Helpful videos about this lesson.