Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Wealth is worthless in the day of wrath, but righteousness delivers from death. Proverbs 11:4 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.5.5, PC.7.2
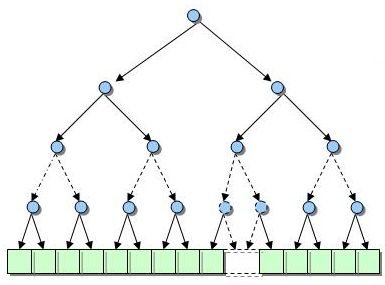
A Christian wants to spread her love for Jesus to others. She tells three people about Jesus who then they each tell two other people each. If each person tells three people about Jesus who then tell three more people. How many total people have been told about Jesus after the 10th set of people have been told about Him? This type of problem is the sum of a geometric series. But first what is a geometric sequence.
A geometric sequence with a pattern of a common ratio, r. The explicit formula can by derived by looking at a simple example.
1, 3, 9, 27, 81, 243, …
Write the numbers using the pattern which in this example is multiplying by 3.
1, 1·3, 1·3·3, 1·3·3·3, 1·3·3·3·3, …
1, 1·31, 1·32, 1·33, 1·34, …
The blue terms are 1 less than the term number, so the rule becomes
an = 1·3n−1
Notice that the first term was 1 and the common ratio was 3, replace those numbers in the rule to get the general formula for the nth term.
an = a1 · rn−1
an = a1 · rn−1
where a1 is the first term and r is the common ratio
a1 = a1, an = r · an−1
Write the rule for the nth term for \(4, -2, 1, -\frac{1}{2}, \frac{1}{4}, …\).
Solution
The first term is 4, so a1 = 4. Divide terms to find the common ratio, r.
$$ -2 ÷ 4 = \color{red}{-\frac{1}{2}}; 1 ÷ -2 = \color{red}{-\frac{1}{2}}; -\frac{1}{2} ÷ 1 = \color{red}{-\frac{1}{2}}; \frac{1}{4} ÷ -\frac{1}{2} = \color{red}{-\frac{1}{2}} $$
It appears that the common ratio is \(-\frac{1}{2}\), so \(r = -\frac{1}{2}\).
an = a1 · rn−1
$$ a_n = 4 · \left(-\frac{1}{2}\right)^{n - 1} $$
Write the rule for the nth term for 3, 6, 12, 24, 48, ….
Answer
an = 3 · 2n−1
The 3rd term of an geometric sequence is 48, and the 6th term is –3072. Write the rule for the nth term.
Solution
This gives two points a3 = 48 and a6 = −3072. Substitute each point into the formula to obtain two equations to solve for a1 and r.
an = a1 · rn−1
$$ \begin{align} \color{blue}{48} &= \color{blue}{a_1 · r^{3 - 1}} \\ \color{red}{-3072} &= \color{red}{a_1 · r^{6 - 1}} \end{align} $$
$$ \begin{align} \color{blue}{48} &= \color{blue}{a_1 · r^{2}} \\ \color{red}{-3072} &= \color{red}{a_1 · r^{5}} \end{align} $$
Because this is a nonlinear system of equations, it must be solved using substitution. Take the first equation and solve it for a1.
48 = a1 · r2
$$ \frac{48}{r^2} = a_1 $$
Substitute this into the second equation.
−3072 = a1 · r5
$$ -3072 = \color{blue}{\frac{48}{r^2}} · r^5 $$
Simplify the powers of r. It is dividing, so subtract the exponents.
−3072 = 48 · r3
−64 = r3
r = −4
Now that r is known, substitute it back into the first equation.
$$ \frac{48}{r^2} = a_1 $$
$$ \frac{48}{\color{blue}{(-4)}^2} = a_1 $$
3 = a1
Now write the rule for the nth term.
an = a1 · rn−1
an = 3 · (−4)n−1
The 2nd term of an geometric sequence is \(\frac{5}{2}\), and the 7th term is \(\frac{5}{64}\). Write the rule for the nth term.
Answer
\(a_n = 5\left(\frac{1}{2}\right)^{n-1}\)
Write the recursive rule for 130, 26, \(\frac{26}{5}\), \(\frac{26}{25}\), ….
Solution
The common ratio appears to be \(\frac{1}{5}\), and the first term is 130. \(r = \frac{1}{5}, a_1 = 130\)
a1 = a1, an = r · an−1
$$ a_1 = 130, a_{n} = \frac{1}{5} · a_{n-1} $$
Write the recursive rule for 5, 15, 45, 135, ….
Answer
a1 = 5, an = 3 · an−1
Deriving the formula for the sum, S, of a geometric series involves some simple factoring.
S = a1 + a1 · r + a1 · r2 + a1 · r3 + a1 · r4 + ⋯ + a1 · rn−1
Multiply both sides by r.
Sr = a1 · r + a1 · r2 + a1 · r3 + a1 · r4 + a1 · r5 + ⋯ + a1 · rn−1 + a1 · rn
Comparing these two first equations, the right side of this equation is S + a1 · rn − a1.
Sr = S + a1 · rn − a1
Sr − S = a1 · rn − a1
Multiply both sides by –1 and rearrange.
S − Sr = a1 − a1 · rn
Factor.
S(1 − r) = a1(1 − rn)
Solve for the sum S.
$$ S_n = a_1 \frac{1 - r^n}{1 - r} $$
Because r∞ ≈ 0 when |r| < 1, if an infinite sum the formula becomes
$$ S_∞ = \frac{a_1}{1-r} $$
$$ S_n = a_1 \frac{1 - r^n}{1 - r} $$
$$ S_∞ = \frac{a_1}{1-r} $$
where |r| < 1
Evaluate \(\displaystyle \sum_{n=1}^{5} 3^{n-1}\).
Solution
This is an geometric series because it is exponential in the form a1 · rn−1. Comparing that to the question, a1 = 1 and r = 3.
$$ S_n = a_1 \frac{1 - r^n}{1 - r} $$
$$ S_5 = 1 \frac{1 - 3^5}{1 - 3} $$
S5 = 121
Evaluate \(\displaystyle \sum_{n=1}^{10} 2\left(\frac{1}{3}\right)^{n-1}\).
Answer
\(\frac{59048}{19683}\)
Find the sum of 8 + 0.8 + 0.08 + 0.008 + ….
Solution
This is an infinite geometric series with a1 = 8 and \(r = \frac{1}{10}\).
$$ S_∞ = \frac{a_1}{1 - r} $$
$$ S_∞ = \frac{8}{1 - \frac{1}{10}} $$
$$ S_∞ = \frac{8}{\frac{9}{10}} $$
$$ S_∞ = \frac{80}{9} $$
Find the sum of 12 + 0.12 + 0.0012 + 0.000012 + ….
Answer
\(\frac{400}{33}\)
Evaluate \(\displaystyle \sum_{n=0}^{∞} 3\left(\frac{1}{4}\right)^n\)
Solution
There are two issues with this problem. The formula is valid for a lower limit of 1 and an exponent of n − 1. Start by fixing the first problem. Evaluate the 0 and then the rest of the sum will then start at 1.
$$ \sum_{n=0}^{∞} 3\left(\frac{1}{4}\right)^n $$
$$ \color{blue}{3\left(\frac{1}{4}\right)^0} + \sum_{n=1}^{∞} 3\left(\frac{1}{4}\right)^n $$
$$ 3 + \sum_{n=1}^{∞} 3\left(\frac{1}{4}\right)^n $$
Fix the second issue, which was making the exponent be n − 1. Exponents are subtracted when dividing with the same base, so divide the expression by the base. But, in order to not change the value of the expression, multiply by the base.
$$ 3 + \sum_{n=1}^{∞} \color{red}{\left(\frac{1}{4}\right)}3\frac{\left(\frac{1}{4}\right)^n}{\color{purple}{\left(\frac{1}{4}\right)^1}} $$
$$ 3 + \sum_{n=1}^{∞} \color{red}{\left(\frac{3}{4}\right)}\left(\frac{1}{4}\right)^{\color{purple}{n-1}} $$
Now the sum is in the correct format with \(a_1 = \frac{3}{4}\) and \(r = \frac{1}{4}\).
$$ S_∞ = \frac{a_1}{1 - r} $$
$$ 3 + \frac{\frac{3}{4}}{1 - \frac{1}{4}} $$
3 + 1 = 4
Note: This is the same answer you would have gotten if you used a1 = 3 and \(r = \frac{1}{4}\) into the infinite sum formula. However, that is mathematically inappropriate because the problem does not fit the requirements of the formula. It is simply a coincidence.
Evaluate \(\displaystyle \sum_{n=0}^{∞} -4\left(\frac{1}{3}\right)^{n}\)
Answer
–6
an = a1 · rn−1
where a1 is the first term and r is the common ratio
a1 = a1, an = r · an−1
$$ S_n = a_1 \frac{1 - r^n}{1 - r} $$
$$ S_∞ = \frac{a_1}{1-r} $$
where |r| < 1
Helpful videos about this lesson.