Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
He heals the brokenhearted and binds up their wounds. Psalms 147:3 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.6.4, PC.7.2
A binomial expression is two terms such as x + y. You already know how to work with binomials including how to calculate exponents of binomials by multiplying the binomial by itself. However, calculating higher exponents of binomials can be long and tedious. The binomial theorem is a shortcut to expand exponents of binomials.
The first 6 powers of (x + y)n are given in the triangle below. The plus signs + between the terms have been removed to simplify the diagram. The coefficients make a triangle called Pascal's Triangle. Blaise Pascal wrote a treatise on the triangle in 1654. However, it was first known in Persia by Al-Karaji and China by Yang Hui around 1000 AD. It is created by adding the two upper numbers to get the one below. Such as the 3 + 3 in the n = 3 row give the 6 in the n = 4 row.
$$ \begin{array}{lcr} (x + y)^0 & 1 & n = 0 \\ (x + y)^1 & 1x \quad 1y & n = 1 \\ (x + y)^2 & 1x^2 \quad 2xy \quad 1y^2 & n = 2 \\ (x + y)^3 & 1x^3 \quad 3x^2y \quad 3xy^2 \quad 1y^3 & n = 3 \\ (x + y)^4 & 1x^4 \quad 4x^3y \quad 6x^2y^2 \quad 4xy^3 \quad 1y^4 & n = 4 \\ (x + y)^5 & 1x^5 \quad 5x^4y \quad 10 x^3y^2 \quad 10 x^2y^3 \quad 5xy^4 \quad 1y^5 & n = 5 \\ & \nearrow \qquad \nearrow \qquad \nearrow \quad \qquad \nearrow \qquad \nearrow \qquad \nearrow \quad & \\ & r=0 \quad r=1 \quad r=2 \quad r=3 \quad r=4 \quad r=5 \quad & \end{array} $$
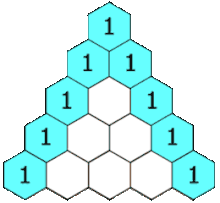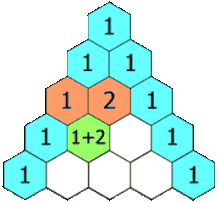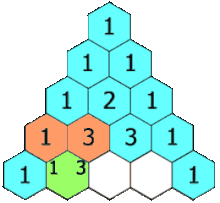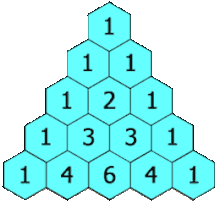
Notice there are some patterns in the triangle.
The binomial coefficients, or combinations, are calculated by \(_nC_r = \frac{n!}{(n-r)!r!}\). This can also be represented \(\left(\begin{matrix} n \\ r \end{matrix}\right)\). Most calculators have a combination function built in.
$$ _nC_r = \frac{n!}{(n-r)!r!} $$
Or another notation.
$$ \left(\begin{matrix} n \\ r \end{matrix}\right) = \frac{n!}{(n-r)!r!} $$
Entered as
n nCr r
Entered as
\(\left(\begin{matrix}\text{n} \\ \text{r}\end{matrix}\right)\)
Evaluate 6C3.
Solution
You can either use the formula or the button on the calculator. First the formula. n = 6, r = 3
$$ _nC_r = \frac{n!}{(n-r)!r!} $$
$$ _6C_3 = \frac{6!}{(6-3)!3!} = 20 $$
You might rather use the calculator function.
On a TI-84, type
¸ nCr  Í
On a NumWorks, input
$$ \left(\begin{matrix} 6 \\ 3 \end{matrix}\right) $$
The output is 20.
Evaluate (a) \(\left(\begin{matrix} 12 \\ 7 \end{matrix}\right)\) and (b) \(\left(\begin{matrix} 5 \\ 2 \end{matrix}\right)\)
Solutions
Evaluate (a) 13C10 and (b) \(\left(\begin{matrix} 8 \\ 1 \end{matrix}\right)\)
Answers
286; 8
The binomial theorem is a shortcut for expanding powers of binomials.
$$ (a + b)^n = \sum_{r=0}^n \ _nC_r a^{n-r} b^r $$
Expand (x + 3)4.
Solution
Compare (x + 3)4 to (a + b)n to see that a = x, b = 3, n = 4. Fill in the binomial theorem with r starting at 0.
$$ \sum_{r=0}^n \ _nC_r a^{n-r} b^r $$
4C0x4−030 + 4C1x4−131 + 4C2x4−232 + 4C3x4−333 + 4C4x4−434
1·x4·1 + 4·x3·3 + 6·x2·9 + 4·x1·27 + 1·x0·81
x4 + 12x3 + 54x2 + 108x + 81
Expand (2 − x3)5.
Solution
Compare (2 − x3)5 to (a + b)n\) to see that a = 2, b = −x3, n = 5. Fill in the binomial theorem with r starting at 0.
$$ \sum_{r=0}^n \ _nC_r a^{n-r} b^r $$
5C025−0(−x3)0 + 5C125−1(−x3)1 + 5C225−2(−x3)2 + 5C325−3(−x3)3 + 5C425−4(−x3)4 + 5C525−5(−x3)5
1·32·1 + 5·16·(−x3) + 10·8·(x6) + 10·4·(−x9) + 5·2·(x12) + 1·1·(−x15)
32 − 80x3 + 80x6 − 40x9 + 10x12 − x15
Expand (2x + 3)3.
Answer
8x3 + 36x2 + 54x + 27
Find the coefficient of the term x5y3 in the expansion of (3x − 2y)8.
Solution
Use the binomial theorem to find the coefficients. a = 3x, b = −2y, n = 8 Because only one coefficient is needed, only one value of r is required. The binomial theorem for each term is
nCran−rbr
Compare this to the desired term x5y3, the exponent of the y should be the same as the exponent of the b part of the formula. Thus r = 3 and we only have to work through the one term.
8C3(3x)8−3(−2y)3
56(243x5)(−8y3)
−108864x5y3
The coefficient of the x5y3 is –108864.
Find the coefficient of the term x4y6 in the expansion of (x − 5y)10.
Answer
3281250
$$ _nC_r = \frac{n!}{(n-r)!r!} $$
Or another notation.
$$ \left(\begin{matrix} n \\ r \end{matrix}\right) = \frac{n!}{(n-r)!r!} $$
Entered as
n nCr r
Entered as
\(\left(\begin{matrix}\text{n} \\ \text{r}\end{matrix}\right)\)
Helpful videos about this lesson.