Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
“Don’t be afraid,” the prophet answered. “Those who are with us are more than those who are with them.” 2 Kings 6:16 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.5.4, PC.7.1, PC.7.3
It is often important to know how likely something is to occur. For example, what is the likely hood of winning the lottery. Give you a hint, you will very likely lose. A general rule of all gambling is that if you play, you will probably lose. The probability is that the organizer of the gambling or lottery will make money because the players lose. Otherwise why go to the effort to organize the games?
Probability is a number from 0 to 1 to indicate how likely something is to happen. 0 means it will never happen, and 1 means it will always happen. Probability is defined as the ratio of favorable outcomes to total possible outcomes. All the possible outcomes is called the sample space.
Number from 0 to 1 indicating how likely something is to happen
0 = Never happen
1 = Always happen
Probability of event A occurring
$$ P(A) = \frac{\text{favorable outcomes}}{\text{total outcomes}} $$
A bag contains 15 US dimes, 3 Canadian dimes, and 2 British ten pence. If a coin is selected at random from the bag, what is the probability of choosing a US dime?
Favorable outcomes are choosing one of the 15 US dimes. Total outcomes are choosing one of the 20 coins.
$$ P(A) = \frac{\text{favorable outcomes}}{\text{total outcomes}} $$
$$ P(US dime) = \frac{15}{20} = 0.75 $$
A clearance bin of movies has 10 good movies, 15 average movies, and 75 bad movies. What is the probability of randomly selecting a good movie?
0.1
In the game of Settlers of Catan, resources are gained by the sum of two rolled dice. Maria built a village on a 5. What is the probability of rolling a 5?
Make a list of all the possible outcomes of rolling two dice. The red is the first die and the blue is the second die.
| 1 1 | 2 1 | 3 1 | 4 1 | 5 1 | 6 1 |
| 1 2 | 2 2 | 3 2 | 4 2 | 5 2 | 6 2 |
| 1 3 | 2 3 | 3 3 | 4 3 | 5 3 | 6 3 |
| 1 4 | 2 4 | 3 4 | 4 4 | 5 4 | 6 4 |
| 1 5 | 2 5 | 3 5 | 4 5 | 5 5 | 6 5 |
| 1 6 | 2 6 | 3 6 | 4 6 | 5 6 | 6 6 |
The 4 shaded outcomes are the favorable outcomes, and there are a total of 36 possible outcomes.
$$ P(A) = \frac{\text{favorable outcomes}}{\text{total outcomes}} $$
$$ P(S = 5) = \frac{4}{36} = 0.44 $$
Two coins are flipped at the same time. What is the probability that one coin is a head and other is a tail?
0.5
Sometimes you need to know the probability of more complicated situations. A compound event is one event with two acceptable outcomes. In the diagram below, either outcome A or outcome B are acceptable. The overlap area is counted twice; once with A and once with B. So the overlap must be subtracted.
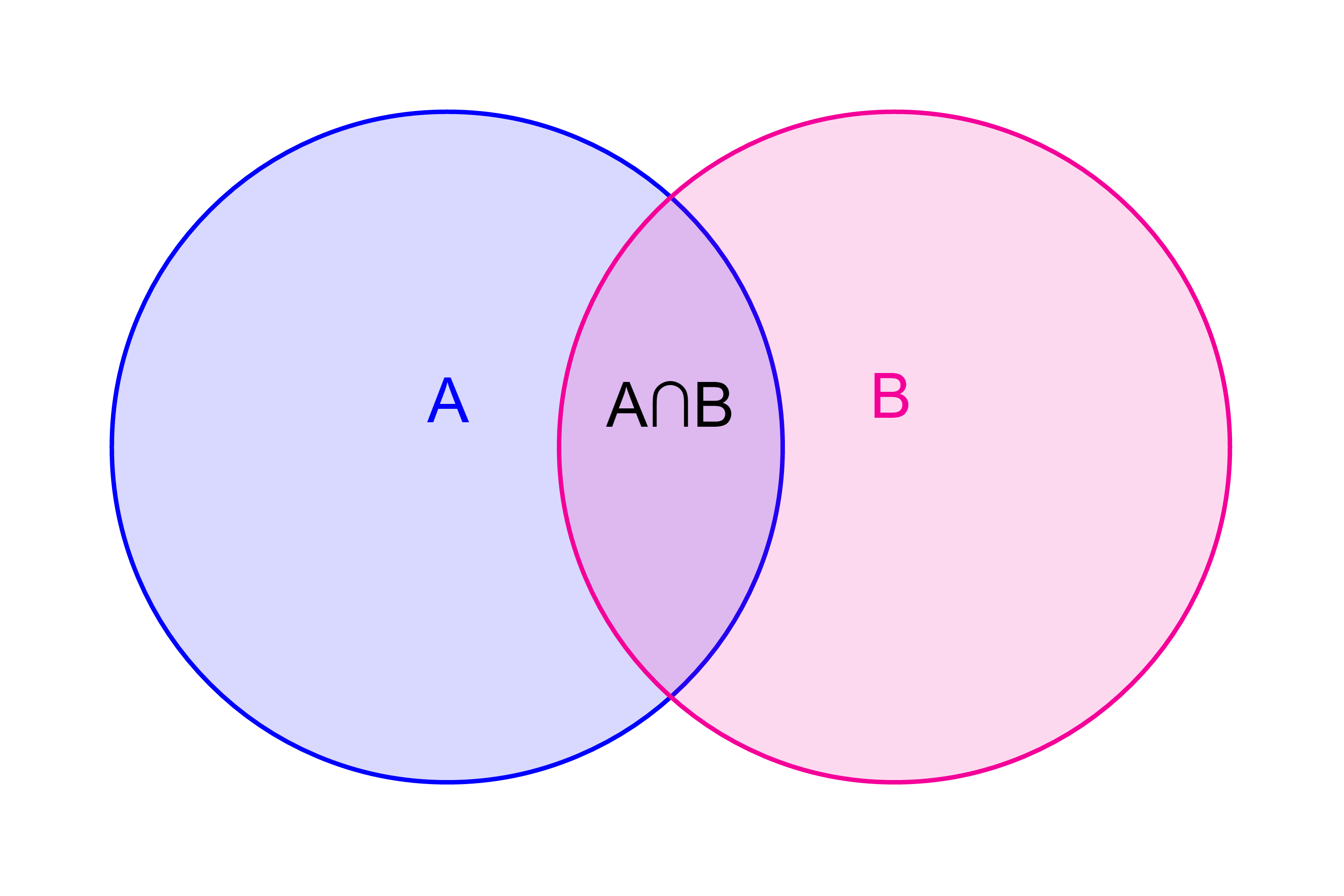
$$ P(A ∪ B) = P(A) + P(B) - P(A ∩ B) $$
The ∪ is the union symbol which means combining all the elements in set A or set B. The ∩ is the intersection symbol which means the overlap of the two sets or all the elements in set A and set B.
If \(P(A ∩ B) = 0\), then the events are called mutually exclusive.
You draw one card from a standard 52-card deck. What is the probability of drawing a spade or a face card?
This is a compound event because it is one event with two acceptable outcomes.
$$ P(♠ ∪ 😃) = P(♠) + P(😃) - P(♠ ∩ 😃) $$
$$ P(♠ ∪ 😃) = \frac{13}{52} + \frac{12}{52} - \frac{3}{52} $$
$$ P(♠ ∪ 😃) = \frac{22}{52} = \frac{11}{26} ≅ 0.42 $$
A coin is tossed and a die is rolled. What is the probability that the coin is a head and the die is a 4?
\(\frac{2}{3} ≈ 0.67\)
Other times, the probability of several events is wanted. In general, to find the probability of multiple events, multiply the probabilities of the individual events together. If the events do not affect each other, then they are independent events. Otherwise, the events are dependent if the events do affect each other.
Independent Events: \(P(A \text{ and } B) = P(A) · P(B)\)
Dependent Events: \(P(A \text{ and } B) = P(A) · P(B|A)\) where \(P(B|A)\) is the probability of B given that A already happened
Two cards are drawn from standard 52-card deck. What is the probability of drawing a spade and a diamond card if (a) with replacement and (b) and without replacement?
With replacement means that the first card is drawn, looked at, then put back in the deck. The deck is then shuffled and the second card is drawn. That makes this question independent.
$$ P(♠ \text{ and } ♦) = P(♠) · P(♦) $$
$$ P(♠ \text{ and } ♦) = \frac{13}{52} · \frac{13}{52} $$
$$ P(♠ \text{ and } ♦) = \frac{1}{4} · \frac{1}{4} = \frac{1}{16} = 0.0625 $$
Without replacement means that the first card is drawn and held, then the second card is drawn. After the first card is drawn, there are less cards to draw, so the probabilities are now different. That makes this situation dependent.
$$ P(♠ \text{ and } ♦) = P(♠) · P(♦|♠) $$
$$ P(♠ \text{ and } ♦) = \frac{13}{52} · \frac{13}{51} $$
$$ P(♠ \text{ and } ♦) = \frac{1}{4} · \frac{13}{51} = \frac{13}{204} ≈ 0.0637 $$
A student guesses on a two question T/F quiz. What is the probability that the student gets both questions correct?
0.25
A complement of a probability is the probability of the opposite. Sometimes it is much easier to find the probability of the opposite of what you are supposed to find. Key words like "at least" or "at most" indicate that finding a complement might be the easiest way to solve the problem.
$$ P(\overline{A}) = 1 - P(A) $$
where \(P(\overline{A})\) is the complement of P(A)
A store has 5 calculators on the rack, but 2 are defective. If you randomly choose two calculators, what is the probability that at least one is defective?
At least one is defective means that 1 is defective or 2 are defective. It is easier to find the opposite which would be 0 defective or both not defective.
$$ P(d ≥ 1) = 1 - P(d = 0) $$
The probability of getting 0 defective calculators is the same as getting 1 good calculator followed by another good calculator without replacement.
$$ P(d = 0) = P(\text{good})P(\text{good}|\text{good}) $$
$$ P(d = 0) = \frac{3}{5} · \frac{2}{4} = \frac{3}{10} $$
Now find the probability of the complement.
$$ P(d ≥ 1) = 1 - P(d = 0) $$
$$ P(d ≥ 1) = 1 - \frac{3}{10} = \frac{7}{10} = 0.7 $$
Your sibling is late to leave for school about 4 times a week. What is the probability that they will be late at least once in a week?
\(\frac{1}{25} = 0.04\)
Number from 0 to 1 indicating how likely something is to happen
0 = Never happen
1 = Always happen
Probability of event A occurring
$$ P(A) = \frac{\text{favorable outcomes}}{\text{total outcomes}} $$
1 event with 2 accepted outcomes (OR)
$$ P(A ∪ B) = P(A) + P(B) - P(A ∩ B) $$
2 or more events (AND)
Independent Events: \(P(A \text{ and } B) = P(A) · P(B)\)
Dependent Events: \(P(A \text{ and } B) = P(A) · P(B|A)\)
Opposite
$$ P(\overline{A}) = 1 - P(A) $$
Helpful videos about this lesson.
Three coins are flipped. Calculate the probability. (Hint: First list the sample space.)
One six-sided die is rolled. Calculate the probability.
One card is drawn from a standard 52-card deck. Calculate the probability.
Two six-sided dice are rolled. Calculate the probability.
Two marbles are drawn from 8 red marbles, 5 blue marbles, and 7 yellow marbles in a bag. Calculate the probability of drawing
Problem Solving
The types of birds at my bird feeder in the morning and afternoon are given in the table.
| Sparrows | Woodpeckers | Doves | Total | |
|---|---|---|---|---|
| Morning | 26 | 4 | 2 | 32 |
| Afternoon | 33 | 5 | 3 | 41 |
| Total | 59 | 9 | 5 | 73 |
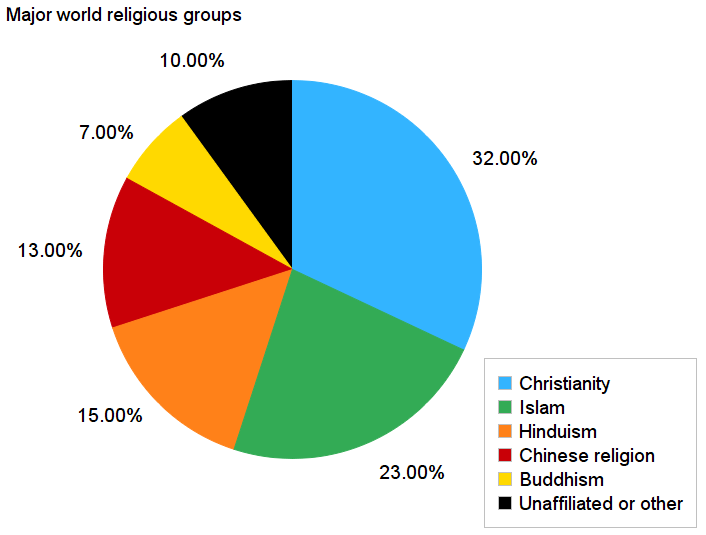
The percent of people following the major world religions is given the circle graph. Data is taken from Pew Research in 2010 when there were 6.9 billion people in the world.
Mixed Review