Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Whoever is kind to the poor lends to the Lord, and he will reward them for what they have done. Proverbs 19:17 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.5.3
Like the roads in this picture, lines can exist in three dimensions. The question is how to describe the lines in three dimensions. Simply adding a z term to Ax + By = C does not work because that describes a plane. The simplest way to describe a three dimensional line is to use vectors.
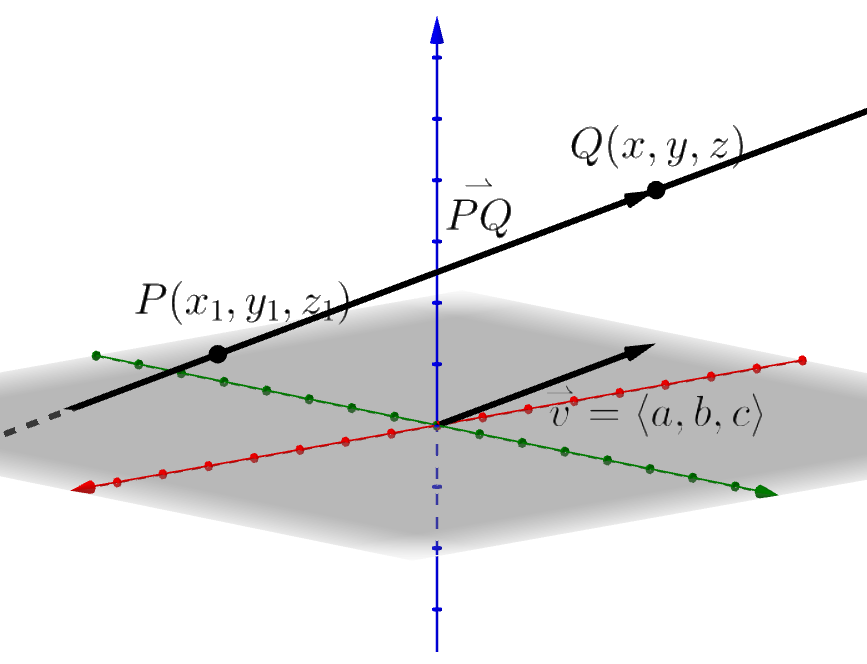
Imagine a line ℓ that goes through points P = (x1, y1, z1) and Q = (x, y, z). Vector \(\overset{\rightharpoonup}{v} = \langle a, b, c \rangle\) is a direction vector for ℓ. To describe the line, start at P and move any distance in direction \(\overset{\rightharpoonup}{v}\) to get some point Q on the line. Because vector \(\overset{\rightharpoonup}{PQ}\) is parallel to \(\overset{\rightharpoonup}{v}\), then \(\overset{\rightharpoonup}{PQ} = t \overset{\rightharpoonup}{v}\). Or in coordinate form
⟨x − x1, y − y1, z − z1⟩ = ⟨at, bt, ct⟩
This is call the general form of a line. The parametric equations of a line are found by making corresponding components of the general form and solving for x, y, or z.
$$ \left\{ \begin{align} x = at + x_1 \\ y = bt + y_1 \\ z = ct + z_1 \end{align} \right. $$
If you remember from lesson 8-03, the parametric form was used to describe the line of solutions when a three-variable system of equations had infinitely many solutions. The parametric equations can all be solved for t and set equal to each other. This produces the symmetric equations of a line.
$$ \frac{x - x_1}{a} = \frac{y - y_1}{b} = \frac{z - z_1}{c} $$
General Form
⟨x − x1, y − y1, z − z1⟩ = ⟨at, bt, ct⟩
Parametric Form
$$ \left\{ \begin{align} x = at + x_1 \\ y = bt + y_1 \\ z = ct + z_1 \end{align} \right. $$
Symmetric Form
$$ \frac{x - x_1}{a} = \frac{y - y_1}{b} = \frac{z - z_1}{c} $$
Find a set of parametric equations of the line that passes through (−2, 1, −3) and (2, 0, 4).
Solution
Find the direction vector between those two points.
$$ \overset{\rightharpoonup}{v} = ⟨2−(-2), 0−1,4−(−3)⟩ $$
= ⟨4, −1, 7⟩
= ⟨a, b, c⟩
Pick one point such as the first point (−2, 1, −3) = (x1, y1, z1). Then plug it into \(\left\{\begin{align} x &= at + x_1 \\ y &= by + y_1 \\ z &= ct + z_1 \end{align}\right.\).
$$ \left\{\begin{align} x &= 4t - 2 \\ y &= -t + 1 \\ z &= 7t - 3 \end{align}\right. $$
Find a set of symmetric equations of the line that passes through (3, 1, 2) and (−2, 0, 1).
Answer
\(\frac{x - 3}{5} = y - 1 = z - 2\)
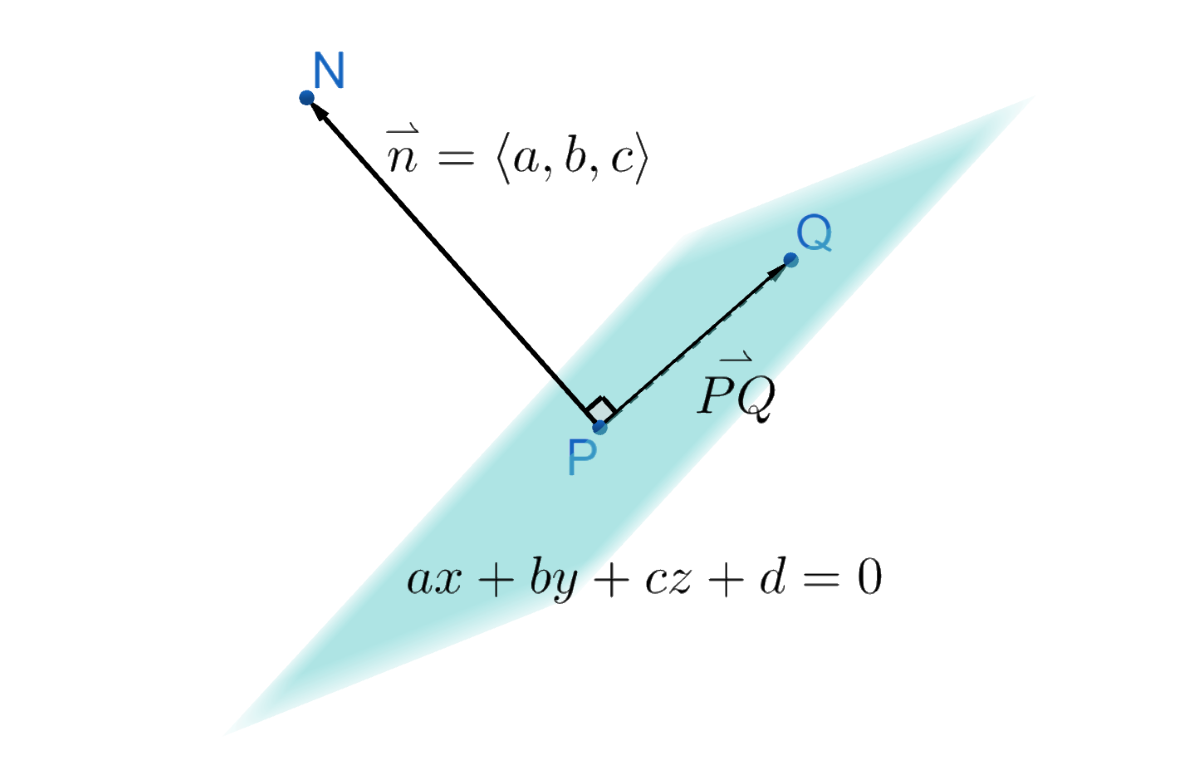
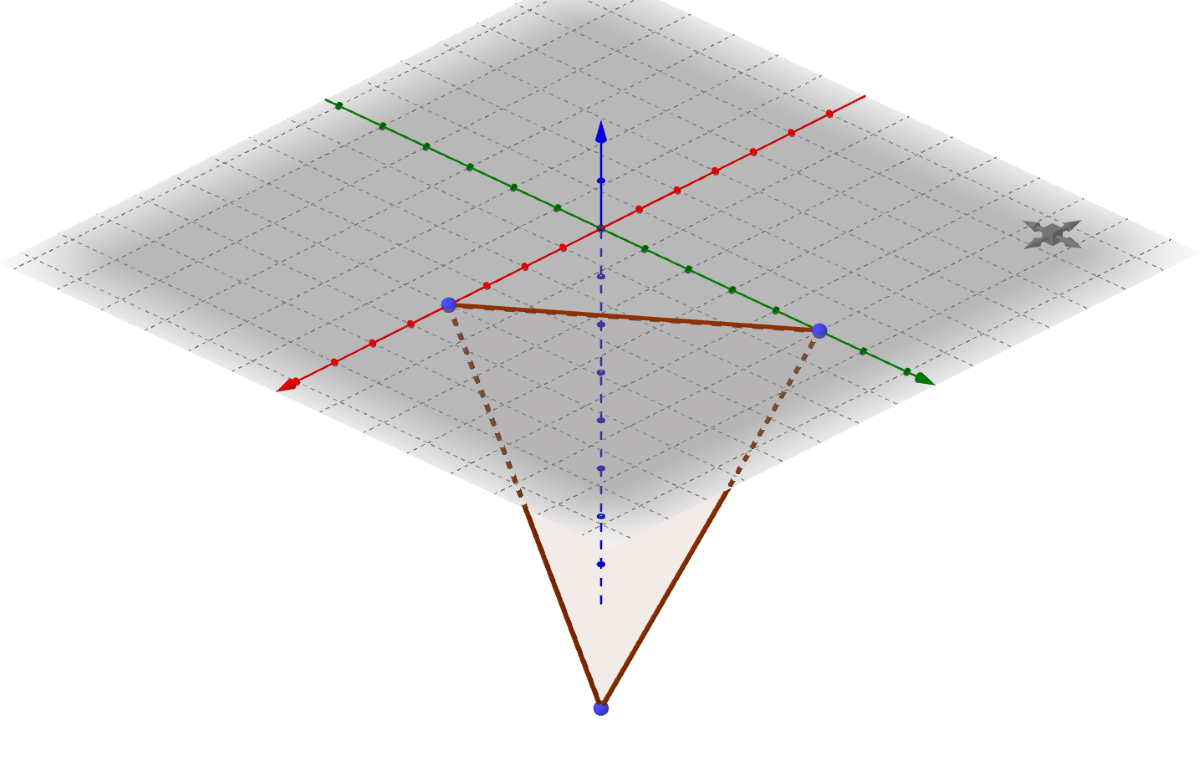
Linear equations in three dimensions graph planes. The easiest way to describe a plane in space is to use a vector that is normal, or perpendicular, to the plane. To see how this works, imagine a vector on the plane, \(\overset{\rightharpoonup}{PQ} = \langle x-x_1, y-y_1, z-z_1 \rangle\), and normal vector to the plane, \(\overset{\rightharpoonup}{n} = \langle a, b, c \rangle\) as in figure 3. Because these vectors are orthogonal (perpendicular), then their dot product is 0.
$$ \overset{\rightharpoonup}{n} \cdot \overset{\rightharpoonup}{PQ} = 0 $$
Calculate the dot product by multiplying the corresponding elements and adding the products. This gives the standard form of a plane.
a(x − x1) + b(y − y1) + c(z − z1) = 0
Distributing and collecting making d = −ax1 − by1 − cz1 produces the general form of a plane.
ax + by + cz + d = 0
If (x1, y1, z1) is a point on the plane and ⟨a, b, c⟩ is a normal vector to the plane, then
a(x − x1) + b(y − y1) + c(z − z1) = 0
ax + by + cz + d = 0
Find the general equation of plane passing through A(1, 2, 0), B(−2, 3, −1), and C(−3, −4, 4)
Solution
Start by finding a vector normal to the plane. Start by using the points to find two vectors in the plane.
$$ \overset{\rightharpoonup}{AB} = \langle -2 - 1, 3 - 2, -1 - 0 \rangle = \langle -3, 1, -1 \rangle $$
$$ \overset{\rightharpoonup}{BC} = \langle -3 - (-2), -4 - 3, 4 - (-1) \rangle = \langle -1, -7, 5 \rangle $$
Then, find the cross product of those two vectors to get the normal vector.
$$ \overset{\rightharpoonup}{n} = \overset{\rightharpoonup}{AB} × \overset{\rightharpoonup}{BC} $$
$$ \overset{\rightharpoonup}{n} = \left| \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ -3 & 1 & -1 \\ -1 & -7 & 5 \end{matrix} \right| $$
$$ \overset{\rightharpoonup}{n} = \left| \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ -3 & 1 & -1 \\ -1 & -7 & 5 \end{matrix} \right| \begin{matrix} \hat{i} & \hat{j} \\ -3 & 1 \\ -1 & -7 \end{matrix} $$
$$ \overset{\rightharpoonup}{n} = 5\hat{i} + \hat{j} + 21\hat{k} - (-\hat{k}) - 7\hat{i} - (-15\hat{j}) $$
$$ \overset{\rightharpoonup}{n} = -2\hat{i} + 16\hat{j} + 22\hat{k} = \langle a, b, c \rangle $$
The normal vector will always be a multiple of this vector even if we chose different points on the plane because all the vectors normal to the plane are parallel to each other.
Next, pick a point on the plane to be (x1, y1, z1) such as point A(1, 2, 0). Fill the point and the normal vector into the standard form of a plane.
a(x − x1) + b(y − y1) + c(z − z1) = 0
−2(x − 1) + 16(y − 2) + 22(z − 0) = 0 $$
Make it look nicer by dividing by the greatest common factor of the coefficients, −2.
(x − 1) − 8(y − 2) − 11z = 0
To get the general form, distribute and collect like terms.
x − 1 − 8y + 16 − 11z = 0
x − 8y − 11z + 15 = 0
Find the general equation of plane passing through A(1, 1, 1), B(−2, 2, 3), and C(0, 3, 2)
Answer
3x − y + 5z − 7 = 0
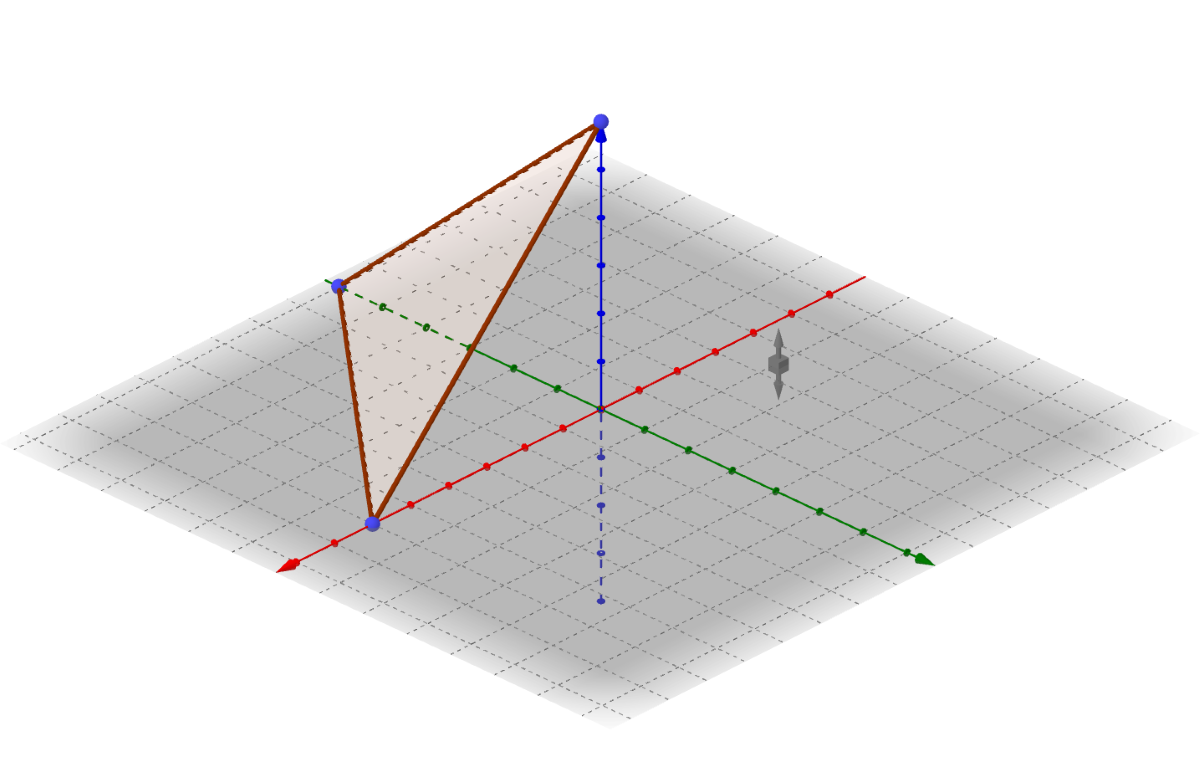
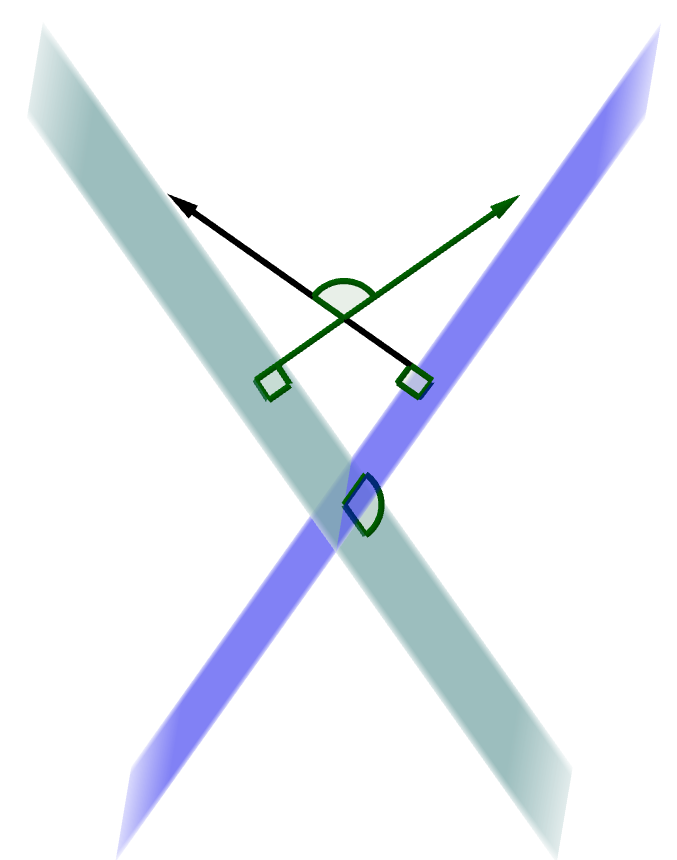
The angle between two planes can be found also using their normal vectors. Figure 4 shows that the angle between the normal vectors is also the angle between the planes. Use the dot product to find the angle between two vectors.
$$ |\overset{\rightharpoonup}{n_1} \cdot \overset{\rightharpoonup}{n_2}| = \| \overset{\rightharpoonup}{n_1} \| \| \overset{\rightharpoonup}{n_2} \| \cos θ $$
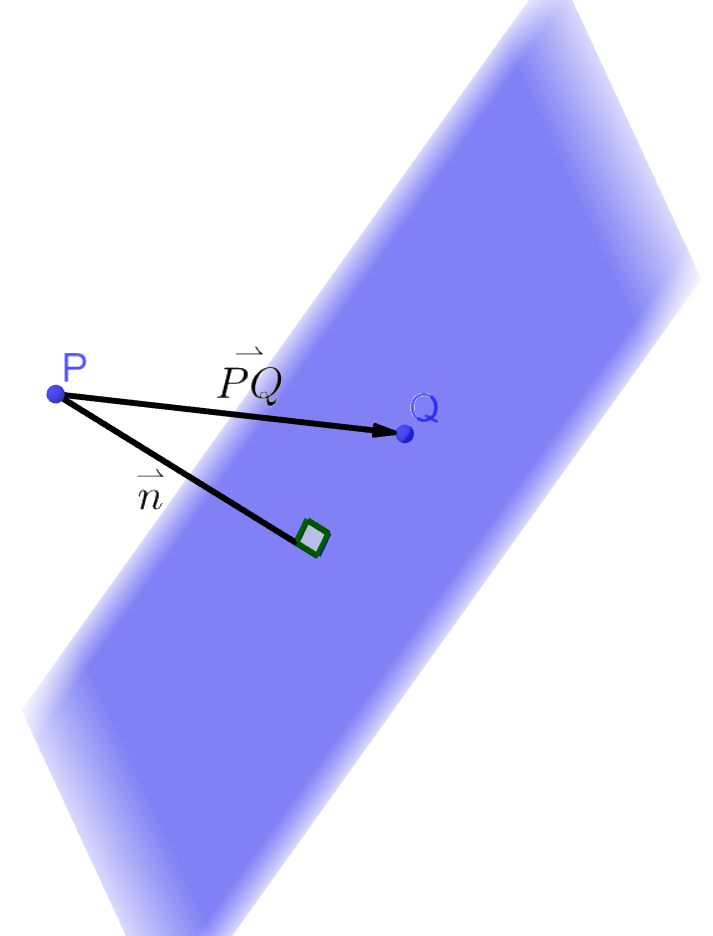
Finding the distance between a point and a plane also involves the normal vector. As figure 5 illustrates, imagine a vector from a point P not on the plane to point Q on the plane. The distance will be the magnitude of the component of vector \(\overset{\rightharpoonup}{PQ}\) that is parallel to the normal vector \(\overset{\rightharpoonup}{n}\). This parallel component is found using a projection.
$$ D = \| \text{proj}_\overset{\rightharpoonup}{n} \overset{\rightharpoonup}{PQ} \| $$
$$ D = \frac{| \overset{\rightharpoonup}{PQ} \cdot \overset{\rightharpoonup}{n} |}{\| \overset{\rightharpoonup}{n} \|} $$
$$ |\overset{\rightharpoonup}{n_1} \cdot \overset{\rightharpoonup}{n_2}| = \| \overset{\rightharpoonup}{n_1} \| \| \overset{\rightharpoonup}{n_2} \| \cos θ $$
where \(\overset{\rightharpoonup}{n_1}\) and \(\overset{\rightharpoonup}{n_2}\) are the normal vectors to the plane.
$$ D = \| \text{proj}_\overset{\rightharpoonup}{n} \overset{\rightharpoonup}{PQ} \| $$
$$ D = \frac{| \overset{\rightharpoonup}{PQ} \cdot \overset{\rightharpoonup}{n} |}{\| \overset{\rightharpoonup}{n} \|} $$
where \(\overset{\rightharpoonup}{n}\) is the normal vector to the plane and \(\overset{\rightharpoonup}{PQ}\) is a vector from the point to a point on the plane.
Find the angle between the planes 2x + y − z + 4 = 0 and 3x − y − 2 = 0.
Solution
The normal vectors are simply the coefficients of the equations of the planes.
$$ \overset{\rightharpoonup}{n_1} = \langle 2, 1, -1 \rangle $$
$$ \overset{\rightharpoonup}{n_2} = \langle 3, -1, 0 \rangle $$
Use the dot product of the normal vectors to find the angle between the planes.
$$ |\overset{\rightharpoonup}{n_1} \cdot \overset{\rightharpoonup}{n_2}| = \| \overset{\rightharpoonup}{n_1} \| \| \overset{\rightharpoonup}{n_2} \| \cos θ $$
$$ |\langle 2, 1, -1 \rangle \cdot \langle 3, -1, 0 \rangle| = \sqrt{2^2 + 1^2 + (-1)^2} \sqrt{3^2 +(-1)^2 + 0^2} \cos θ $$
$$ 5 = \sqrt{6}\sqrt{10} \cos θ $$
θ ≈ 49.8°
Find the angle between the planes x − y + 4z + 1 = 0 and 2x + 5z − 7 = 0.
Answer
15.7°
Find the distance between the point (5, 3, −2) and the plane x + 2y − z − 4 = 0.
Solution
Start be finding \(\overset{\rightharpoonup}{PQ}\), but to do that a point on the plane is needed. A simple point to find would be the x-intercept. Plug in 0 for y and z to find it.
x + 2y − z − 4 = 0
x + 2(0) − (0) − 4 = 0
x = 4
So a point on the plane is (4, 0, 0). Now find \(\overset{\rightharpoonup}{PQ}\).
$$ \overset{\rightharpoonup}{PQ} = \langle 5 - 4, 3 - 0, -2 - 0 \rangle = \langle 1, 3, -2 \rangle $$
The normal vector is the coefficients of the equation of the plane.
$$ \overset{\rightharpoonup}{n} = \langle 1, 2, -1 \rangle $$
Find the projection of \(\overset{\rightharpoonup}{PQ}\) onto \(\overset{\rightharpoonup}{n}\).
$$ D = \frac{| \overset{\rightharpoonup}{PQ} \cdot \overset{\rightharpoonup}{n} |}{\| \overset{\rightharpoonup}{n} \|} $$
$$ D = \frac{| \langle 1, 3, -2 \rangle \cdot \langle 1, 2, -1 \rangle |}{\sqrt{1^2 + 2^2 +(-1)^2}} $$
$$ D = \frac{| 1 + 6 + 2 |}{\sqrt{6}} $$
$$ D = \frac{9\sqrt{6}}{6} = \frac{3\sqrt{6}}{2} $$
Find the distance between the point (6, −5, 1) and the plane x − y + 4z + 1 = 0.
Answer
\(\frac{8\sqrt{2}}{3}\)
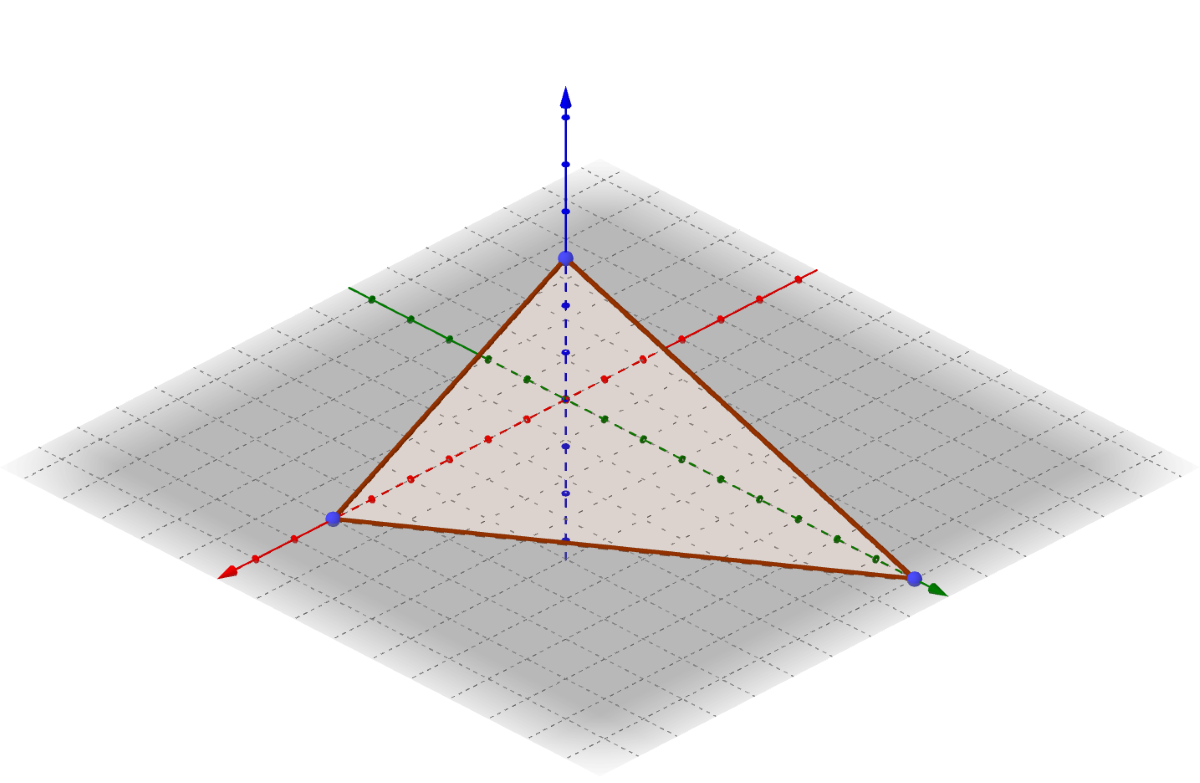
Graphing planes in space is difficult because the plane extends forever. One method that is often used is to graph only the part of the in one of the octants. Start by finding all the intercepts. Then plot intercepts. Finally connect the intercepts to form a triangle and lightly shade it. However, realize that the plane continues forever. This triangle simply represents the plane.
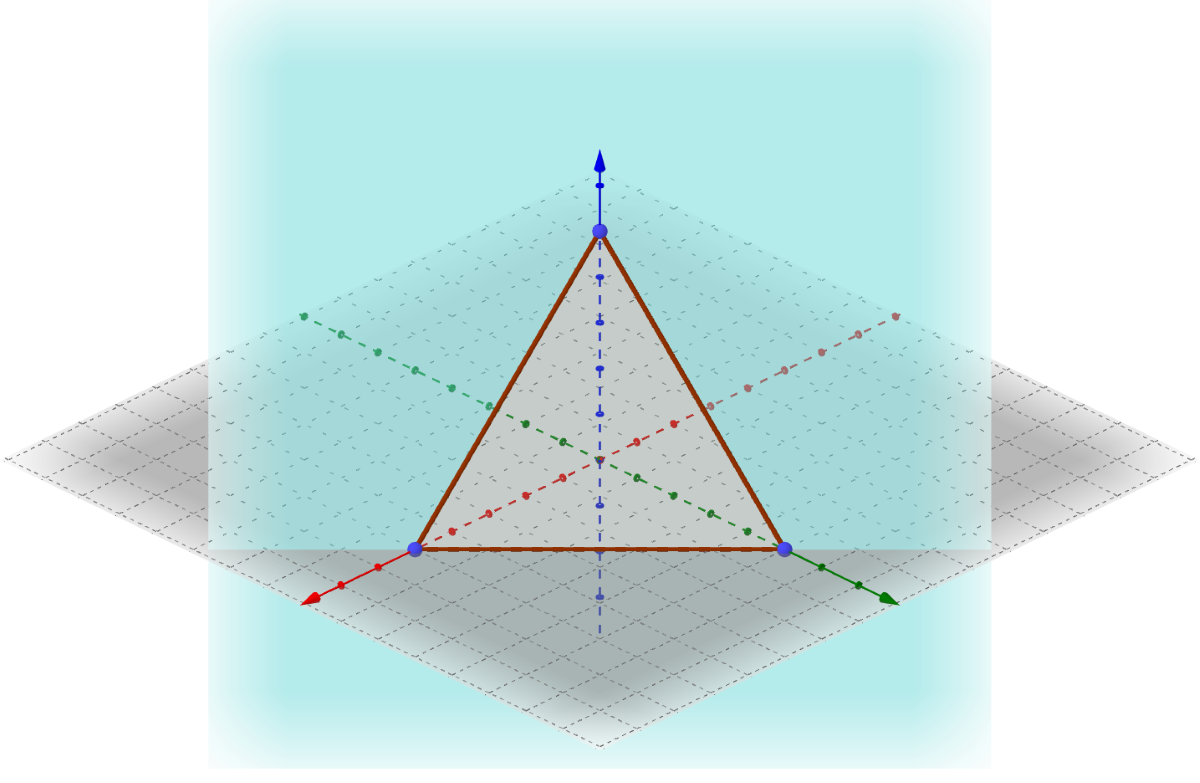
Sketch 4x + 6y + 3z = 24.
Solution
Start by finding the intercepts by letting the other variables be 0.
x-int: 4x + 6(0) + 3(0) = 24 → x = 6 → (6, 0, 0)
y-int: 4(0) + 6y + 3(0) = 24 → y = 4 → (0, 4, 0)
z-int: 4(0) + 6(0) + 3z = 24 → z = 8 → (0, 0, 8)
Graph those three points and connect them to form a triangle. Lightly shade the triangle.
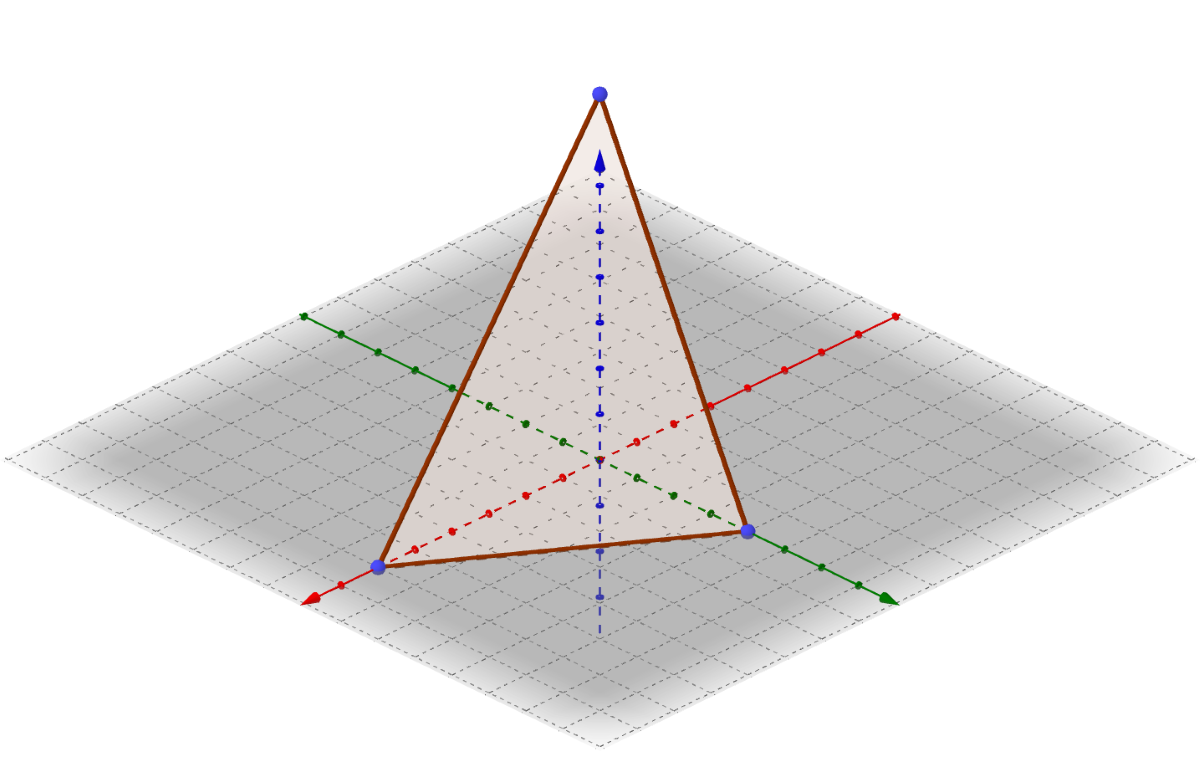
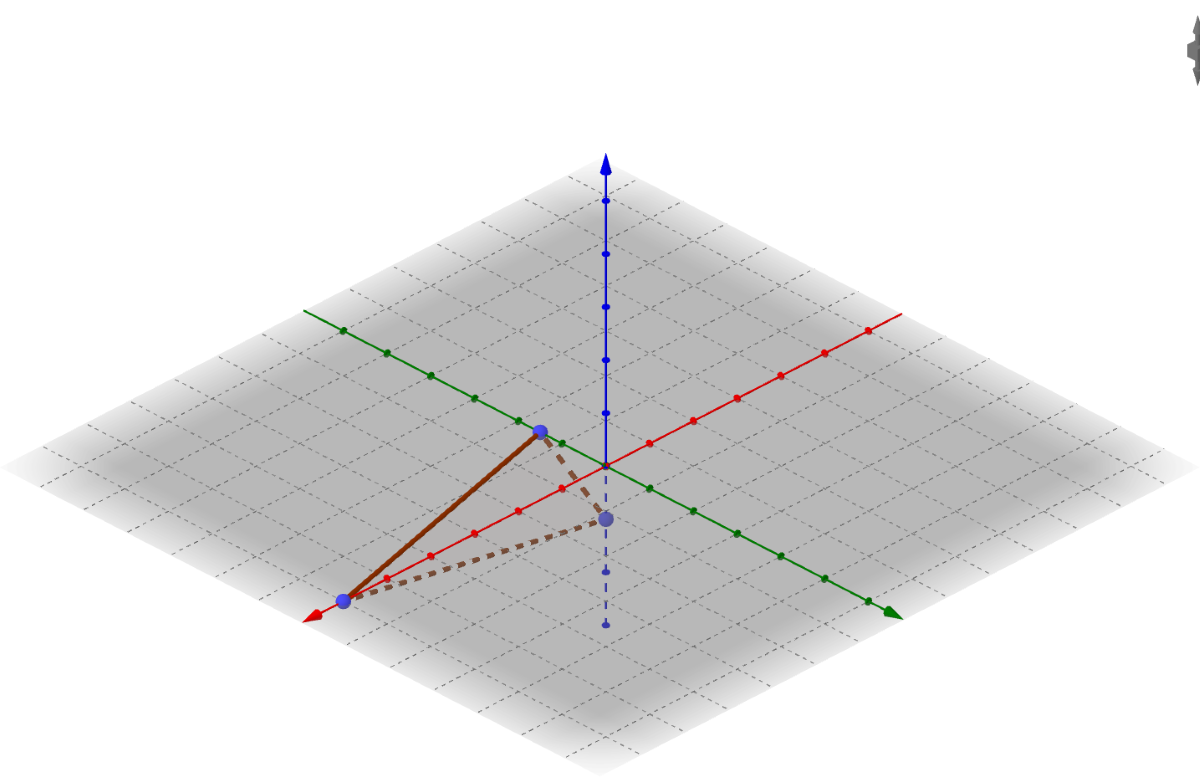
Sketch 3x − 12y − 18z = 36.
Answer
General Form
⟨x − x1, y − y1, z − z1⟩ = ⟨at, bt, ct⟩
Parametric Form
$$ \left\{ \begin{align} x = at + x_1 \\ y = bt + y_1 \\ z = ct + z_1 \end{align} \right. $$
Symmetric Form
$$ \frac{x - x_1}{a} = \frac{y - y_1}{b} = \frac{z - z_1}{c} $$
If (x1, y1, z1) is a point on the plane and ⟨a, b, c⟩ is a normal vector to the plane, then
a(x − x1) + b(y − y1) + c(z − z1) = 0
ax + by + cz + d = 0
$$ |\overset{\rightharpoonup}{n_1} \cdot \overset{\rightharpoonup}{n_2}| = \| \overset{\rightharpoonup}{n_1} \| \| \overset{\rightharpoonup}{n_2} \| \cos θ $$
where \(\overset{\rightharpoonup}{n_1}\) and \(\overset{\rightharpoonup}{n_2}\) are the normal vectors to the plane.
$$ D = \| \text{proj}_\overset{\rightharpoonup}{n} \overset{\rightharpoonup}{PQ} \| $$
$$ D = \frac{| \overset{\rightharpoonup}{PQ} \cdot \overset{\rightharpoonup}{n} |}{\| \overset{\rightharpoonup}{n} \|} $$
where \(\overset{\rightharpoonup}{n}\) is the normal vector to the plane and \(\overset{\rightharpoonup}{PQ}\) is a vector from the point to a point on the plane.
Helpful videos about this lesson.
