![[The sum over i from 1 to n of i =n(n+1)/2]](../webtexts/trinum.gif)
where mathematicians use the capital Greek letter ![[Sigma]](../webtexts/sum.gif)
(sigma) to represent summation.
Your teacher has a particular fondness for this symbol
since the first computer he had much
access to had that nickname.
| Descriptive statistics generally characterizes or describes a set of data elements by graphically displaying the information or describing its central tendancies and how it is distributed. |
The last half of the course will cover inferential statistics.
|
Inferential statistics tries to infer information about a
population by using information gathered by sampling. |
|
Statistics: The collection of methods
used in planning an experiment and analyzing data in order to draw accurate conclusions. |
| Population: The complete set of data elements is termed the population. |
The term population will vary widely with its application. Examples could be any of the following proper subsets: animals; primates; human beings; homo sapiens; U.S. citizens; who are attending Andrews University, as graduate students, in the School of Education, as Masters students, female, last name starting with S, who web registered.
| Sample: A sample is a portion of a population selected for further analysis. |
How samples are obtained or types of sampling will be studied in lesson 7. Most any of the examples above for population could serve as a sample for the next higher level data set.
| Parameter: A parameter is a characteristic of the whole population. |
| Statistic: A statistic is a characteristic of a sample, presumably measurable. |
The plural of statistic just above is another basic meaning of statistics.
Assume there are 8 students in a particular statistics class, with 1 student being male. Since 1 is 12.5% of 8, we can say 13% are male. The 13% represents a parameter (not a statistic) of the class because it is based on the entire population. If we assume this class is representative of all classes, and we treat this 1 student as a sample drawn from a larger population, then the 13% becomes a statistic.
| Remember: Parameter is to Population as Statistic is to Sample. |
Inferential statistics is used to draw conclusions about a population by studying a sample. It is not guesswork! We test hypotheses about a parameter's value with a certain risk of being wrong. That risk is carefully specified. Also, descriptive and inferential statistics are not mutually exclusive. The inferences made about a population from a sample help describe that population. We also tend to use Roman letters for statistics and Greek letters for parameters.
An interesting subset of the natural numbers generated by addition are called Triangular Numbers. These are so called because these are the total number of dots, if we arrange the dots in a triangle with one additional dot in each layer.
| • | ||||||
| • | • | |||||
| • | • | • | ||||
| • | • | • | • |
Suppose we wish to add together the first 100 natural numbers, which is equivalent to finding the 100th triangular number. One way to do this is by grouping them as follows:
| T100 | = | (1 +100) + (2+99) + (3 + 98) + ... + (50 + 51) |
| = | 101• 50 | |
| = | 101• 100/2 |
In general we write:
where mathematicians use the capital Greek letter
(sigma) to represent summation.
Your teacher has a particular fondness for this symbol
since the first computer he had much
access to had that nickname.
There are three important rules for using the summation operator:
Example: Cx1 + Cx2 + ... + Cxn = C(x1 + x2 + ...+ xn)
Example: 4 + 4 + 4 + 4 + 4 = 5 × 4 = 20.
Example: Joe got scores of 500 and 550 for his verbal and quantitative SAT scores whereas Jim got scores of 520 and 510, respectively. 500 + 550 + 520 + 510 = 1050 + 1030 = 500 + 520 + 550 + 510 = 1020 + 1060 = 2090.
Exponentiation is a general term which includes
squaring (122=144), cubing (63=216),
and square roots (16½=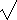
(16)=4.
When the square root symbol (surd and symbol of inclusion, in recent history a vinculum,
but historically parentheses) is used,
we general (although not quite always) mean only the positive square root.
The absolute value operator indicates the distance (always non-negative)
a number is from the origin (zero). The symbol used is a vertical
line on either side of the operand. Thus, if x>0, then |x|=x,
if x<0, then |x|=-x, and if x=0, |x|=0.
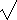(x2)=|x|.
There is a proscribed order for arithmetic operations to be performed.
Example: If we write 4 × 5 + 3 it is conventional to multiply the 4 and 5 together before adding the 3 and thus obtain 23. Some calculators are algebraic and handle this appropriately, others do not.
Parentheses and other symbols of inclusion are used to modify the normal order of operations. We say these symbols of inclusion have the highest priority or precidence.
Exponentiation is done next. There is confusion when exponents are stacked which we will not deal with here except to say computer scientists tend to do it from left to right while mathematicians know that is wrong.
Multiplication and Division are done next, in order, from left to right.
Addition and Subtraction are done next, in order, from left to right.
A mnemonic such as Please Eat Miss Daisy's Apple Sauce can be useful for remembering the proper order of operation.
This ties in with significant figures, and proper rounding of results. I have several major concerns regarding significant digits.
| Qualitative data are nonnumeric. |
{Poor, Fair, Good, Better, Best}, colors (ignoring any physical causes), and types of material {straw, sticks, bricks} are examples of qualitative data.
Qualitative data are often termed catagorical data. Some books use the terms individual and variable to reference the objects and characteristics described by a set of data. They also stress the importance of exact definitions of these variables, including what units they are recorded in. The reason the data were collected is also important.
| Quantitative data are numeric. |
Quantitative data are further classified as either discrete or continuous.
| Discrete data are numeric data that have a finite number of possible values. |
A classic example of discrete data is a finite subset of the counting numbers, {1,2,3,4,5} perhaps corresponding to {Strongly Disagree... Strongly Agree}.
Another classic is the spin or electric charge of a single electron. Quantum Mechanics, the field of physics which deals with the very small, is much concerned with discrete values.
When data represent counts, they are discrete. An example might be how many students were absent on a given day. Counts are usually considered exact and integer. Consider, however, if three tradies make an absence, then aren't two tardies equal to 0.67 absences?
| Continuous data have infinite possibilities: 1.4, 1.41, 1.414, 1.4142, 1.141421... |
The structure and nature of data will greatly affect our choice of analysis method. By structure we are referring to the fact that, for example, the data might be pairs of measurements. Consider the legend of Galileo dropping weights from the leaning tower of Pisa. The times for each item would be paired with the mass (and surface area) of the item. Something which Galileo clearly did was measure the time it took a pendulum to swing with various amplitudes. (Galileo Galilei is considered a founder of the experimental method.)
| Nominal: Nominal data have no order and thus only gives names or labels to various categories. |
| Ordinal: Ordinal data have order, but the interval between measurements is not meaningful. |
| Interval: Interval data have meaningful intervals between measurements, but there is no true starting point (zero). |
| Ratio: Ratio data have the highest level of measurement. Ratios between measurements as well as intervals are meaningful because there is a starting point (zero). |
Nominal comes from the Latin root nomen meaning name. Nomenclature, nominative, and nominee are related words. Gender is nominal. (Gender is something you are born with, whereas sex is something you should get a license for.)
Example 1: Colors
To most people, the colors: black, brown, red, orange, yellow,
green, blue, violet, gray, and white are just names of colors.
To an electronics student familiar with color-coded resistors, this data is in ascending order and thus represents at least ordinal data.
To a physicist, the colors: red, orange, yellow, green, blue, and violet correspond to specific wavelengths of light and would be an example of ratio data.
Example 2: Temperatures
What level of measurement a temperature is depends on which temperature
scale is used.
Specific values: 0°C = 32°F = 273.15 K = 491.69°R
100°C = 212°F = 373.15 K = 671.67°R
-17.8°C = 0°F = 255.4 K = 459.67°R
where C refers to Celsius (or Centigrade before 1948);
F refers to Fahrenheit; K refers to Kelvin; R refers to Rankine.
Only Kelvin and Rankine have true zeroes (starting point) and ratios can be found. Celsius and Fahrenheit are interval data; certainly order is important and intervals are meaningful. However, a 180° dashboard is not twice as hot as the 90° outside temperature (Fahrenheit assumed)! Rankine has the same size degree as Fahrenheit but is rarely used. To interconvert Fahrenheit and Celsius, see Numbers lesson 12. (Note that since 1967, the use of the degree symbol on tempertures Kelvin is no longer proper.)
Although ordinal data should not be used for calculations, it is not uncommon to find averages formed from data collected which represented Strongly Disagree, ..., Strongly Agree! Also, averages of nominal data (zip codes, social security numbers) is rather meaningless!
| BACK | HOMEWORK | NO ACTIVITY | CONTINUE |
|---|