An event with a probability of 1 is certain.
0
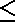 P(A)
P(A) 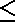 1 for any event A.
1 for any event A.
| Ensure that the sample size is large enough. |
Although a large sample is no guarantee of avoiding bias, too small a sample is a recipe for disaster. How to determine minimum sample size will be at least touched on in lesson 11 (Hinkle chapter 13). There are well established techniques to determine such. These techniques are based on the Central Limit Theorem discussed later in this lesson.
| Better results are obtained by measuring instead of asking. |
A good classroom example would be to collect people's heights. We expect heights might be normally distributed. Asking will result in several sources of error. Perhaps the most common being exaggeration, rounding, hair style, and shoe heel variation or even complete absence of shoes. The units of measure: inches; feet and inches; or centimeters isn't obvious either. Were you instead to measure each individual, these sources of error could be reduced. You may still encounter systematic errors. Following are some sources of systematic error. Perhaps your measuring device is defective. Specific examples might include the common fact that rulers often don't start exactly at zero, but have a little extra margin. Maybe the measuring tape is marked off in inches on one side and tenth's of a foot on the other and sometimes the wrong side is read. Tape measures can become kinked or even tangled (especially surveying caves). Perhaps being a statistics students correlates with being shorter or taller for some unknown reason. This might only be a problem if you were to use your data to represent a larger population.
| The medium used (mail, phone, personal interview) is important. |
Surveys are a very popular method of data collection for social issues. Mail surveys tend to have a lower response rates which will distort and hence flaw a sample. Although telephone surveys may be relatively efficient and inexpensive, the more time consuming and correspondingly expensive personal interview allows more detailed and complex data to be collected. Be not called by telemarketers.
| Be sure the sample is representative of the population. |
An observational study observes individuals and measures variables of interest but does not attempt to influence the responses. An experiment deliberately imposes some treatment on individuals in order to observe their responses. Observational studies are then a poor way to gauge the effect of an intervention. When our goal is to understand cause and effect, experiments are the only source of fully convincing data. However, imposing treatments may produce some ethical concerns. See more below under experimental design.
Before we move on to the next point, we should note that some studies are retrospective, or involve looking back at past events, whereas others are prospective or track groups forward in time.
Statisticians have classified sampling into five common types, as follows.
| Random Sampling: Members of the population are chosen in such a way that all have an equal chance to be measured. |
Other names for random sampling include representative and proportionate sampling because all groups should be proportionately represented. Consider what might happen if a telephone directory were used as a source for randomly selecting survey participants. Some people have no phone, others have multiple phones and corresponding listings. Still others have unlisted phone numbers. In affluent areas unlisted phone numbers may approach half the population! Now-a-days many are giving up lands lines and use cell phone exclusively. Cell phone directories are controversial at best. Pollsters commonly use computers to generate and dial phone numbers in an attempt to circumvent these problems. However, many people consider such use of the telephone as an invasion of their privacy and refusals or hang-ups may well significantly influence the outcome. Some of us have learned to recognize these computer dialers and quickly hang up. Such are the pitfalls which must be carefully considered in designing an experiment, study, or survey.
Simple random sampling is the least complex and probably the most widely used sampling technique in behavior science research. The word simple here differentiates this sampling technique from other more complex sampling techniques.
| A simple random sample or SRS consists of n elements from the population chosen in such a way that every set of n individuals has an equal change of being the sample actually selected. |
Random sampling must be a structured event to ensure no bias. These are not haphazardly done, done on the spur of the moment, or done as a matter of convenience. In general no randomization no generalization. Since the point of taking the sample is generally to generalize the results to the parent population, the randomization step is extremely important. A sampling technique which starts out random may lose such a status as it is processed. For example, suppose surveys are mailed out and some recipients fail to return a completed survey. Worse yet, suppose a mail sack was lost or stolen so no one from Wyoming even got theirs.
| Systematic Sampling: Every kth member of the population is sampled. |
The historic event leading to the word decimate, where every 10th Roman soldier was killed, is a gruesome example of systematic sampling.
The reciprocal of the sampling fraction (the ratio of the size of the sample to the population: (n/N) determines the k (N/n) used. Once k has been determined, the index of a starting element is selected within the first k elements by random selection. The indices for subsequent elements are formed by adding multiples of k to this starting index. The sampling continues until we reach the end of the list at which time n elements will have been selected. There are technicalities for handling non-integer ks which add some complexity.
Note how there are now only k different samples possible. This limitation is often of little consequence when one considers the difficult procedures often necessary to obtain a simple random sample and in most situations these samples can be treated as SRSs as long as no periodic factors bias the sample within the list. Alphabetic lists of peoples names are generally free of periodic factors even though family names and ethnicity (van, Mc) may cause some clustering within the list.
| Stratified Sampling: The population is divided into two or more strata and each subpopulation is sampled (usually randomly). |
Stratum is the singular form of the word strata which means to spread out. One of the word's most common usage is in geology to describe the layers of sedimentary rocks which have formed during the earth's history. Gender and age groups would be commonly used strata. Classes is another term for strata. Each stratum must share the same characteristic. Random sampling may well be used to select a certain number of data points from each stratum. This sometimes is the most efficient sampling method.
Stratified sampling takes advantage of some inhomogeneity (heterogeneity) of a population, whereas random and systematic sampling generally assume the population is homogeneous. One often knows how the population is distributed among these different strata and then usually proportionally allocates the sample accordingly. Although this might seem an advantage, the random sampling process tends to generate similar results. However, stratified sampling will ensure that no strata are missed. Stratified random sampling will enhance statisitical precision, which is a desirable outcome.
| Cluster Sampling: A population is divided into clusters and a few of these (often randomly selected) clusters are exhaustively sampled. |
Exhaustively means considering all elements. Cluster sampling is used extensively by governmental and private research organizations. These clusters are naturally formed groups such as families, classrooms, or even schools. Hopefully, population elements belong to one and only one cluster. Multistage sampling is common with cluster sampling. An example might be a two-stage sample in which precincts are randomly selected, followed by the random selection of blocks of residents within these precincts. All residents then within these selected blocks would be sampled.
| Convenience Sampling: Sampling is done as convenient, often allowing the element to choose whether or not it is sampled. |
Convenience sampling is the easiest and potentially most dangerous. Often good results can be obtained, but perhaps just as often the data set may be seriously biased. Consider collecting GPA information from students in detention. It may be convenient, but perhaps not representative of the entire student body!
| Be wary of convenience sampling. |
Of great debate recently was what to do with the errors which arise in the decennial US Census. Considerable time was spent by all three branches of our government addressing this issue.
| An experiment is a method by which observations are made. |
A famous example of an experiment is when Benjamin Franklin, famous American statesman and scientist, determined whether electricity is conducted. The experiment involved flying a kite in a thunder (and lightning) storm with a wire from the kite to a key in a bottle. (Don't try this at home!) (Also, questions have arisen as to whether or not he actually performed this experiment. It seems others did it earlier, only his son may have been present, and his journals don't support well this event occurring.) The experimental method is now the basis of the scientific method. In statistics we often refer to a random experiment, one for which there is no way of telling beforehand what the outcome will be.
|
The act of rolling a fair die, flipping an honest coin, or randomly selecting a card from a deck are all considered random experiments. |
An interesting part of mathematics is the use of common language to describe mathematical concepts. One such example is the word event. Normally, event conjures up images of special moments: the prom, banquets, fairs, weddings, births, .... In dealing with probability, event has a very precise meaning.
|
An event is the set of outcomes from a random experiment. A simple event is an outcome which cannot be broken down. The sample space is the set of all possible outcomes for a given experiment. |
| \ | T | H |
|---|---|---|
| T | TT | HT |
| H | TH | HH |
Rolling a standard six-sided (fair) die once would have a sample space with six outcomes: 1, 2, 3, 4, 5, and 6. Rolling a pair of dice would have a sample space of six times six (62) or 36 possible outcomes. In the activity for lesson 2 we constructed the sample space of rolling a pair of dice and plotted the distribution of the sum of pips (See Hinkle, Figure 7.3).
For some interactive web sites involving rolling dices, flipping or spinning coins check out these links. Be forewarned, however, that if cards or a roulette wheel are involved your internet search is likely to lead you to gambling sites (casinos) whose legality on the web has been and is being challenged due to its addictive nature and those many lives which have been ruined thereby.
| Probability is denoted by P and specific
events by A, B, or C. The shorthand notation used to indicate the probability that event B occurs is P(B). Empirical (Experimental) Definition of Probability: P(A) = number of times A occurred divided by the times the experiment was repeated.
Classical Definition of Probability: |
The probability of something occurring is related to its frequency. Specifically, when a coin is flipped twice in succession, in 1 of the 4 possible outcomes heads appeared both times. Thus the probability was ¼ or 0.25. It is important to remember that the probability of A occurring is less than or equal to one. We have tacitly assumed here that the probability of heads is equal to that of tails. Experiments have been conducted to test this. In such a case, the probability would then be an experimental rather than a theoretical result.
|
An event with a probability of 0 is impossible. An event with a probability of 1 is certain. 0 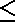 P(A) P(A) 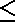 1 for any event A.
1 for any event A. |
Probabilities for random events might be computed exactly. In such case we express them as fractions. Other probabilities are obtained by experiment and are thus approximations which are typically expressed to three significant digits unless there are compelling reasons for more or less precision. Probabilities are often given as percentages. When doing so be sure to include the percentage symbol (%) since technically probabilities are always between 0 and 1 inclusive. For example, certainty corresponds with 100% and impossibility with 0%.
| Probability can be approximated by frequency: P(A) = number of times A occurred divided by number of times experiment is repeated. |
We used the term fair above to describe coins or dies yielding an equal likelihood for any outcome. Thus a fair coin has a 50% of turning up heads and a 50% chance of turning up tails. This is often expressed in terms of odds as 50-50. Each of the two outcomes is equally likely and thus had a probability of ½. On rare occasions a coin might end up on its side, but generally we exclude such events from the set of outcomes we are considering, just as we generally consider only the genders of male and female. We would thus expect a six sided die to have a 1/6 probability for any face to be on top. Again, the rare chance of balancing on an edge or corner will generally be excluded, as will be outcomes where the result cannot be determined (such as the die falling into a black hole or sewer grate).
| If an experiment is repeated over and over, then the empirical probability approaches the actual probability. |
The above statement is often stated as a theorem known as the Law of Large Numbers. Determining sample size is an exercise in optimizing tradeoffs in cost and accuracy. Large samples should be more accurate but will be more costly, whereas smaller samples cost less but provide less accuracy. Those who have not studied statistics tend to scoff at the idea that a survey of only 1000 (0.001%) people in this country of 100 million voters can give a good estimate of how many favor a particular candidate or position. Of course, if your sample is not random, biases will creep in, and accuracy will suffer. Later lessons will explore these concepts in greater detail.
Example: Assume you have 20 M&M® brand candies as follows:
5 orange, 6 yellow, 5 red, and 4 green.
In one selection, how many ways can you select either 1 orange or
1 yellow M&M®? What is the corresponding probability?
Answer: Of the 20 M&M's®, 5 are orange and 6 are yellow.
Hence 5+6=11 of the M&M's® are yellow or orange.
The probability of selecting a yellow or orange M&M® is 11/20=0.55.
The M&M's® are either one color or another, hence getting a certain color is mutually exclusive of getting a different color—that is, no M&M's® are rainbow-colored, zebra-striped, or some shade such as orange-yellow or blue-green which thus might be judged different colors by different people. To clarify further the meaning of mutually exclusive, let's say that only one or another event can occur, never both at the same time.
Example: Assume you have 20 M&M's® color distributed as above.
If selected without replacement, in how many ways can you select
two red ones in two selections?
What is the corresponding probability?
Answer: For the first selection, five of the 20 M&M's® are red.
Since we need to get two reds in only two selections, we need only
consider this successful case further, ignoring what happens if
we do not get a red on this first selection.
For the second selection, only four red of the 19 M&M's® remain.
Hence there are 5•4=20 ways of selecting two reds M&M's®
in two selections. The corresponding probability would be:
(5/20)•(4/19)=20/380=1/19 or approximately 0.0526.
The first example above (OR) will be dealt with further below. We will now discuss the second example (AND then). We noted above repeated coin flips and die rolls. The size of our sample space, that is the set of all possible outcomes, was the product of the set of possible outcomes for each event: 2•2=4 for two coin flips and 6•6=36 for rolling two dice.
This is often referred to as the Multiplication Rule. It can only be applied if the events are independent. For more on that subject see below.
|
If event A can occur in m possible ways
and event B can occur in n possible ways, there are m•n possible ways for both events to occur. n(A and then B)=n(A)×n(B) |
This is generally expressed as event A and then event B occurring. This is an AND situation where both are performed. This calculation extends to three or more events. For example, if event C can occur in o possible ways, there are m•n•o possible ways for these three events to turn out.
Example: How many different ways can parents have three children.
Answer: For each child we will assume there are only two possible
outcomes (thus neglecting effects of extra X or Y chromosomes, or any other
chromosomal/birth defects). The
number of ways can be calculated: 2•2•2 = 8.
These can be listed: BBB, BBG, BGB, BGG, GBB, GBG, GGB, GGG where
B=boy, G=girl. We could have just as well used the symbols 0 and 1:
000, 001, 010, 011, 100, 101, 110, 111. Note that this is the same
as counting in base 2. This fact can be used to more easily list
outcomes or to check for missing outcomes (exactly 4 have boy first,
exactly 4 have boy second, exactly 4 have boy last, etc).
Another way to represent this information is in tree form with
the branches from each node representing the possibilities for
the next event (see below).
Note that this can become very large and thus listing
or displaying the complete sample space is often impractical.
This is often referred to as the Addition Rule.
|
If event A can occur in m possible ways
and event B can occur in n possible ways, there are m+n possible ways for either event A or event B to occur, but only if there are no events in common between them. n(A or B)=n(A)+n(B)-n(A |
Because often one works with non-overlapping events, you will find that the last term is commonly omitted, but added later. It is better to learn the formula correctly the first time and make a special case when the intersection is indeed empty. An empty intersection might occur due to happenstance or it might occur because the events cannot occur simultaneously, i.e. the events are mutually exclusive. In the M&M® example above, the color selections were mutually exclusive.
In the homework you will look at an example of overlapping events when you calculate the probability of the green die having a 2 or the red die of having a 5. A careful inspecation of the diagram in the prior lesson indicates that although there are six outcomes where the green die has a 2 and six outcomes where the red die has a 5, we must be careful not to double count the event where both the green die has a 2 and the red die has a 5. There are thus only 11 not 12 corresponding outcomes and the probability was 11/36 or about 0.306.
Example: Suppose you have four candles you wish to arrange from left to right
on your dinner table. The four candles are vanilla, mulberry,
orange, and raspberry fragrances (shorthand: V, M, O, R).
How many options do you have?
Solution: If you select V first then you still have three options remaining.
If you then pick O, you have two candles to choose from.
You can compute the number of ways to decorate your table by the factoral rule:
for the first choice (event) you have 4 choices;
for the second, 3;
for the third, 2;
and for the last, only 1.
The total ways then to select the four candles are: 4!=4•3•2•1 = 24.
These types of problems occur frequently and can be summarized as follows.
| Factorial Rule: For n different items, there are n! arrangements. |
Try solving this exercise on your own: You need to study, practice football, fix dinner, phone a friend, and go buy a notebook. How many different ways can you arrange your schedule?
Permutation is another name for possible arrangements with SOME items from a given set. It is important to remember that order chosen or position arranged is taken into account. Hence permutations are similar to anagrams. Given below is the necessary equation.
|
nPr = n! / (n - r)! where r is the number of items arranged from n elements. |
More information on permutations, permutations with repeated elements, and permutations on a circle can be found at this location.
|
nCr = n! / (r!(n - r)!) where r is the number of items taken from n elements. |
Note that these numbers are the same as those in Pascal's Triangle, the binomial formula, and the binomial distribution. Those less than about four digits become very familiar.
Example: You have five places left for stamps in your stamp book and
you have eight stamps. How many different ways can you select five?
Answer: 8!/(5!3!) = 8•7•6/(3•2)=56.
Think of putting them in slots, the first has eight choices,
the next slot has seven choices and so forth as demonstrated.
|
P(A and B) = P(A)·P(B)
if A and B are independent. P(A and B) = P(A)·P(B|A) if A and B are dependent. |
Sometimes the probability of A and B occurring is given, but the question asks for the probability of B occurring after A. All that requires is solving the algebraic equation, P(A and B) = P(A)·P(B|A) for P(B|A), the conditional probability.
Tree diagrams are a method of double checking your work when the sample space is small.
Example: A couple plans on having 3 children.
What is the probability of them having two boys and one girl?
Answer:
| B ---- B ---B |
| ---G |
| ---- G ---B |
| ---G |
| G ----- B ---B |
| ---G |
| ---- G ---B |
| ---G |
| 2 × 4 = 8 |
In the chart, there are three different ways to have two boys and one girl. Thus the probability is 3/8 or 0.375. One can also think of the only girl being born first, second, or third. We can do it in a different way: P(GBB) + P(BGB) + P(BBG) = ½×½×½ + ½×½×½ + ½×½×½ = 1/8 + 1/8 + 1/8 = 3/8. Of course, those of us who have done this awhile immediately think in terms of Pascal's Triangle and nCr!
Example: What is the probability of rolling a die twice and
getting two sixes?
Answer: P(6)·P(6) = 1/6 × 1/6 = 1/36 = 0.0278.
Example:
A local theater group is planning to give away a season ticket via a raffle.
Eighty women dropped their ticket stubs in the bucket while only 35 men did.
What is the probability of the winning ticket not going to a woman?
Solution: Thirty-five men dropped their stubs of the 115 total tickets.
P(not getting a woman) = P(man) = 35/115 = 7/23 = 0.304.
Example:
A person deals you a new five card hand. What is the probability
of having at least one heart?
Solution: P(at least one heart) = 1 - P(none) =
1 - 13C0•39C5 ÷ 52C5 =
1 - (39/52)(38/51)(37/50)(36/49)(35/48)
= 1 - 0.222 = 0.778.
Just think how long it would have taken if instead you calculated
the probabilities for getting
one heart, two hearts...!
Please note, the method used above for computing none is very general and not well nor widely documented. I'm referring specifically to the expression: 13C0•39C5 ÷ 52C5. This expression is saying of the 13 hearts we choose 0, whereas of the other 39 cards we choose 5. These two items are multipied together then divided by the number of ways to choose 5 cards from 52. Thus to calculate the probability for getting one heart would be: 13C1•39C4 ÷ 52C5.
|
P(A) + P(Ã) = 1 P(Ã) = 1 - P(A) P(A) = 1 - P(Ã) |
Seven, eleven, or doubles may get you out of jail in Monopoly, but a close examination of the 36 possible outcomes when two dies are rolled and the pips summed indicates these have probabilities of 6/36, 2/36, and 6/36 for a total of 7/18=0.389. The corresponding probability for getting out on the second turn is (7/18)2=0.151. The corresponding randomness gives variety to the game just as randomness gives variety to statistical results. However, there is an underlying distribution which can be analyzed.
The underlying distribution of possible outcomes is important when we consider the probability of any specific sample. We will briefly look at a few theoretical distributions which are commonly encountered.
Consider the combinations examined above and apply it specifically to the case of selecting six of ten when the ten are five males and five females. Any number, say x, between 1 and 5, inclusive, could occur with 6 - x of the other gender occurring. However, if we examine the distribution of the 10C6 = 210 different possibilities we discover 5C5•5C1 = 5 ways five women and one man might be selected, 5C4•5C2 = 50 ways four women and two men might be selected, 5C3•5C3 = 100 ways three women and three men might be selected, and the remaining results are symmetric hence given above. This is a very leptokurtic distribution (Hinkle Figure 7.4).
Another common underlying distribution is the binomial distribution which we already examined in homework 4 problem 1 with the flipping of four coins and gave some formulae in lesson 4. This is a special case in the family of binomial distributions for a given number of trials, where p=q=½. It is natural to ask what happens when p#q#½. The same formula as before applies, namely:
| P(x) = nCx • px • qn-x where x = 0, 1, 2,..., n |
Example: Find the probability of having five left-handed students in a
class of twenty-five, given p=0.1
(n = 25, x = 5, p = 0.1).
Solution:
P(5) = (25! ÷(20! · 5!)) •(0.1)5 • (0.9)20
= 0.064593.
Thus, the probability that 5 of the 25 students will be left-handed is about 6%. As usual, it is important to set up your solution logically. Carefully identify the important values (n, x, p, etc.) before cranking out the numbers and presenting your answer. The TI-83/84 series calculators have BINOMPDF which, if given the two arguments of n and p, in that order, will output a list of n+1 probabilities for each value of x, with the first one being for x=0. BINOMCDF is similar but gives cumulative frequency. Both are under the 2nd VARS or DISTR button (entries 0 and A, so you may need to scroll down). It can be shown that the mean, variance, and standard deviation of a binomial distribution can be expressed in simple formulae as follows:
|
Example: Suppose 20 biased coins are flipped and each
coin has a probability of 75% of coming up heads. Find
the mean and standard deviation for this binomial experiment.
Solution: n=20, p=0.75, so q=¼.
![]() =n · p = 20 · 0.75 = 15.
This is as expected, we expect heads to come up about three quarters the time.
=n · p = 20 · 0.75 = 15.
This is as expected, we expect heads to come up about three quarters the time.
![]() =
=
![]() (n · p · q) =
(n · p · q) =
![]() (20 · 0.75 · ¼) =
(20 · 0.75 · ¼) =
![]() 3.75
3.75
![]() 1.936.
1.936.
Since the binomial distribution tends to become more like the normal distribution as sample size increases, especially when p and q are nearly equal, we can often approximate the binomial using the normal distribution. More information can be found here which we will summarize by saying np and nq must be greater than 10 (or 5 or 15) before this can be done.
The normal distribution is the most important underlying distribution due to is prevalence in such measurements as intelligence, aptitude, and achievement. In addition, many of the statistics generated through inferential statistics are normally distributed or close to normally distributed.
The center, width, and variability of the sampling distribution of the mean is determined by the central limit theorem.
| Central Limit Theorem: As sample size increases, the sampling distribution of sample means approaches that of a normal distribution with a mean the same as the population and a standard deviation equal to the standard deviation of the population divided by the square root of n (the sample size). |
Stated another way, if you draw simple random samples (SRS) of size n
from any population whatsoever with mean ![]() and finite standard deviation
and finite standard deviation ![]() ,
when n is large, the sampling distribution of the sample means
,
when n is large, the sampling distribution of the sample means
![]() is close to a
normal distribution with mean
is close to a
normal distribution with mean ![]() and standard deviation
and standard deviation ![]() /
/
![]() (n).
This standard deviation is often called the
standard error of the mean.
(n).
This standard deviation is often called the
standard error of the mean.
It is important to recognize that this standard error of the mean decreases as sample size increases. This means increased precision with larger sample size. However, to improve the precision by a factor of 2 would require an increase in the sample size by a factor of 4.
A second result is that the shape of the sampling distribution of the mean resembles more closely a normal distribution as the sample size increases, even when the population is not normal.
The sampling distribution in the case above of sample means becomes the underlying distribution of the statistic. It is an important component in the chain of reasoning which underpins inferential statistics. Different sampling distributions will apply to different sample parameters. The study of inferential statistics is largely an examination of which distribution applies to which parameter and developing a familiarity with this distribution and how to apply an appropriate statistical test.
| BACK | HOMEWORK | ACTIVITY | CONTINUE |
|---|