![[graph of bell-shaped curve]](../webtexts/gaussian.gif)
The prefix bi- has the usual meaning of two in this context, just like bicycle, bifocal, and bigamist. This distribution is related to what happens when you study the expansion of the binomial (1+x)n. Here it means there are two and only two distinct categories. For instance, students either pass or they fail a test. In dining out at fast food restaurants, people either have or haven't eaten at McDonald's.
Some notation has become very standard when working with binomial distributions. S (success) and F (failure) denote possible categories for all outcomes; whereas, p and q=1-p denote the probabilities P(S) and P(F), respectively. The term success may not necessarily be what you would call a desirable result. For example, you may want to find the probability of finding a defective chip, given the probability 0.2 that a chip is defective. Here the term success might actually represent the process of selecting a defective chip. The important thing here is to correlate P(S) with p. Some authors avoid q, but the formulae seem clearer using it rather than the awkward expression 1-p.
The requirements to be a binomial experiments are as follows:
|
Requirement 2 specifically implies with replacement if we are selecting something, unless the change of not replacing it is slight.
|
| P(x) = nCx • px • qn-x where x = 0, 1, 2,..., n |
Here nCx has the usual definition as entries from Pascal's Triangle and can be defined in terms of n! divided by (x! • (n-x)!). The symbol !, the factorial symbol as shorthand for the product of all the natural numbers up to that number. Thus, 4!=4 · 3 · 2 · 1 = 24. By definition and convention, 0!=1. Note that if p=q=½, the distribution will be symmetric due to the symmetry in Pascal's Triangle. In chapter 7 we will examine some cases where p does not equal q, i.e. p#½.
Example: 10 coins are flipped and each coin has a probability of 50% of
coming up heads. What is the distribution of expected number of heads up?
Solution: From Pascal's Triangle we find row 10 gives us the
follow: 1, 10, 45, 120, 210, 252, 210, ....
This tells us how many different arrangements there are that have
0, 1, 2, 3, etc. heads. There are 210=1024
different arrangements total and so the corresponding probabilities are:
| x | 10Cx| 10Cx½10
| 0 | 1 | 9.77E-4
| 1 | 10 | 0.00977
| 2 | 45 | 0.0439
| 3 | 120 | 0.117
| 4 | 210 | 0.205
| 5 | 252 | 0.246
| 6 | 210 | 0.205
| 7 | 120 | 0.117
| 8 | 45 | 0.0439
| 9 | 10 | 0.00977
| 10 | 1 | 9.77E-4
| |
|---|
As the number of coin flips increases, the binomial distribution, although discrete, looks more and more like the normal distribution.
![[pi]](../webtexts/pi.gif) ), where e is the
transcendental number 2.71828... and
), where e is the
transcendental number 2.71828... and
![[pi]](../webtexts/pi.gif) is the more familiar,
but also transcendental number 3.14159....
The
is the more familiar,
but also transcendental number 3.14159....
The ![[pi]](../webtexts/pi.gif) in the formula only serves to
normalize the total area under the curve.
When we normalize something, we make it equal
to some norm or standard, usually one (1).
The word normal has several other meanings, including
perpendicular and the usual/status quo.
in the formula only serves to
normalize the total area under the curve.
When we normalize something, we make it equal
to some norm or standard, usually one (1).
The word normal has several other meanings, including
perpendicular and the usual/status quo.
![[graph of bell-shaped curve]](../webtexts/gaussian.gif)
| The standard normal distribution |
The height of the curve represents the probability of the
measurement at that given distance away from the mean.
The total area under the curve being one represents the fact
that we are 100% certain (probability = 1.00) the measurement
is somewhere. Technically, this is the standard normal
curve which has
µ=0.0 and 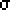 =1.0.
Other applications of the normal curve do not have this restriction.
For example, intelligence has often been cast, albeit controversially,
as normally distributed with
µ=100.0 and
=1.0.
Other applications of the normal curve do not have this restriction.
For example, intelligence has often been cast, albeit controversially,
as normally distributed with
µ=100.0 and ![[sigma]](../webtexts/sigma.gif) =15.0.
This is represented below. Our function has been modified to
y=e-(x-µ)2/2
=15.0.
This is represented below. Our function has been modified to
y=e-(x-µ)2/2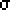 2/
(
2/
(![[sigma]](../webtexts/sigma.gif)
![]() (2
(2![[pi]](../webtexts/pi.gif) ))
))
| Normally distributed IQs | ![[graph of iq distribution]](../webtexts/iqdist.gif)
|
Other things which may take on a normal distribution include body temperature, shoe sizes, diameters of trees, etc. It is also important to note the symmetry of the normal curve. Some curves may be slightly distorted or truncated beyond certain limits, but still primarily conform to a "heap" or "mound" shape. This is often an important consideration when analyzing data or samples taken from some unknown population.
We need to differentiate between a set of data which is normally distributed and THE normal distribution. THE normal distribution is a gold standard to which other distributions are compared, whereas various sets of data may follow, to a good approximation, the normal distribution and hence be termed normally distributed. Many procedures of inferential statistics depend on the underlying data being somewhat normally distributed and/or the various samples possible having a high probability of being normal as well.
![[+/- 1 std shaded under normal curve]](../webtexts/gauss1sd.gif)
| Data within 1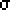 (left) and 2 (left) and 2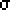 (right) (right)
| ![[+/- 2 std shaded under normal curve]](../webtexts/gauss2sd.gif)
|
The author usually claims an IQ of at least 145. We can see from the above information that this would put him at least three standard deviations above the population mean (100+3•15=145). Hence, if we accept the hypothesis that IQs are normally distributed, at least 99.85% of the population would have a lower IQ and less than 0.15% a higher one. Please especially note that if 99.7% of the population is within three standard deviations of the mean, the remaining 0.3% is distributed with half beyond three standard deviations below the mean and the other half beyond three standard deviations above the mean. This is a result of the symmetry (due to the fact that x is squared, it matters not if it is positive or negative) of the curve. In practical terms, in a population of 250,000,000; 249,625,000 would have an IQ lower than 145 and 375,000 would have an IQ higher. Because of the small area of these regions, they are often referred to as tails. Depending on the circumstances, we may be interested in one tail or two tails.
Several societies exist which cater to individuals with high IQs. Some specific examples would be MENSA, Triple Nine, Mega, etc.
Another important charateristic of this distribution is that it is
of infinite extent. In practical terms, IQs below 0 (-6.67 )
or above 210 (7.33
)
or above 210 (7.33 )
(ceiling scores such as
Marilyn Vos Savant's
are difficult to interpret)
do not occur. A recently popularized manufacturing goal has been termed
Six Sigma.
One would think this would corresponds with about 3.4 defects per billion,
but their web site implies it is 200 per million. A typically
good company operates at less than four sigma or 99.997% perfect.
This corresponds closer to 32 defects per million. If you have
ever purchased a "lemon"
(a colloquialism for bad car, perhaps one built on a Monday)
you can appreciate such striving for perfection.
Other similar examples would be the large increase in
errors related to prescription drugs being dispensed
or the case of the Florida patient who had the wrong leg amputated.
)
(ceiling scores such as
Marilyn Vos Savant's
are difficult to interpret)
do not occur. A recently popularized manufacturing goal has been termed
Six Sigma.
One would think this would corresponds with about 3.4 defects per billion,
but their web site implies it is 200 per million. A typically
good company operates at less than four sigma or 99.997% perfect.
This corresponds closer to 32 defects per million. If you have
ever purchased a "lemon"
(a colloquialism for bad car, perhaps one built on a Monday)
you can appreciate such striving for perfection.
Other similar examples would be the large increase in
errors related to prescription drugs being dispensed
or the case of the Florida patient who had the wrong leg amputated.
|
For K=2,
we see that 1-1/22=1-1/4=3/4,
which is 75% of the data must always be within two standard deviations of the mean. |
|
For K=3,
we see that 1-1/32=1-1/9=8/9,
which is about 89% of the data must always be within three standard deviations of the mean. |
If we consider the data set 50, 50, 50, and 100, we will discover that the sample standard deviation (s) is 25, and the upper score falls exactly at 2s above the rest. However, since the mean is 62.5, it is well within 2s. Added 5 more scores of 50 we find the mean is now 55.6 and the standard deviation now 16.7. We see that two standard deviations above the mean now extends to 88.9 and we have one data point outside that, but within three standard deviations. The general concept of being able to find the mean of a data set and determine how much of it is within a certain distance (number of standard deviations) of the mean is an important one which will carry over into inferential statistics.
The table below gives values for the area between z=0 and z=?, where the final z is initially read down, then the value at the top of the column is added. Alternately, the value at the top of the column can be viewed as the second digit. Such tables may clarify why z scores are so typically reported to two decimal places! Warning: Although every effort has been made to verify these numbers (on a TI-83 graphing calculator), errors may still be present. Also, the table is somewhat incomplete due to lack of space.
| z | x.x0 | x.x1 | x.x2 | x.x3 | x.x4 | x.x5 | x.x6 | x.x7 | x.x8 | x.x9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0x | .0000 | .0040 | .0080 | .0120 | .0160 | .0199 | .0239 | .0279 | .0319 | .0359 |
| 0.1x | .0398 | .0438 | .0478 | .0517 | .0557 | .0596 | .0636 | .0675 | .0714 | .0753 |
| 0.2x | .0793 | .0832 | .0871 | .0910 | .0948 | .0987 | .1026 | .1064 | .1103 | .1141 |
| 0.3x | .1179 | .1217 | .1255 | .1293 | .1331 | .1368 | .1406 | .1443 | .1480 | .1517 |
| 0.4x | .1554 | .1591 | .1628 | .1664 | .1700 | .1736 | .1772 | .1808 | .1844 | .1879 |
| 0.5x | .1915 | .1950 | .1985 | .2019 | .2054 | .2088 | .2123 | .2157 | .2190 | .2224 |
| 0.6x | .2257 | .2291 | .2324 | .2357 | .2389 | .2422 | .2454 | .2486 | .2517 | .2549 |
| 0.7x | .2580 | .2611 | .2642 | .2673 | .2704 | .2734 | .2764 | .2794 | .2823 | .2852 |
| 0.8x | .2881 | .2910 | .2939 | .2967 | .2995 | .3023 | .3051 | .3078 | .3106 | .3133 |
| 0.9x | .3159 | .3186 | .3212 | .3238 | .3264 | .3289 | .3315 | .3340 | .3365 | .3389 |
| 1.0x | .3413 | .3438 | .3461 | .3485 | .3508 | .3531 | .3554 | .3577 | .3599 | .3621 |
| 1.1x | .3643 | .3665 | .3686 | .3708 | .3729 | .3749 | .3770 | .3790 | .3810 | .3830 |
| 1.2x | .3849 | .3869 | .3888 | .3907 | .3925 | .3944 | .3962 | .3980 | .3997 | .4015 |
| 1.3x | .4032 | .4049 | .4066 | .4082 | .4099 | .4115 | .4131 | .4147 | .4162 | .4177 |
| 1.4x | .4192 | .4207 | .4222 | .4236 | .4251 | .4265 | .4279 | .4292 | .4306 | .4319 |
| 1.5x | .4332 | .4345 | .4357 | .4370 | .4382 | .4394 | .4406 | .4418 | .4429 | .4441 |
| 1.6x | .4452 | .4463 | .4474 | .4484 | .4495 | .4505 | .4515 | .4525 | .4535 | .4545 |
| 1.7x | .4554 | .4564 | .4573 | .4582 | .4591 | .4599 | .4608 | .4616 | .4625 | .4633 |
| 1.8x | .4641 | .4649 | .4656 | .4664 | .4671 | .4678 | .4686 | .4693 | .4699 | .4706 |
| 1.9x | .4713 | .4719 | .4726 | .4732 | .4738 | .4744 | .4750 | .4756 | .4761 | .4767 |
| 2.0x | .4772 | .4778 | .4783 | .4788 | .4793 | .4798 | .4803 | .4808 | .4812 | .4817 |
| … | … | … | … | … | … | … | … | … | … | … |
| 3.0x | .4987 | .4987 | .4987 | .4988 | .4988 | .4989 | .4989 | .4989 | .4990 | .4990 |
Example: Find the probability for a data value to fall
between the mean (z=0.00) and one standard deviation (z=1.00)
above the mean, assuming the population is normally distributed.
Solution: The table above gives the value 0.3413 or 34.13%.
This is the same as what the empirical rule gives (68÷2).
Example: Find the probability for IQ values between 75 and 130,
assuming a normal distribution, mean = 100 and std = 15.
Solution: An IQ of 75 corresponds with a z score of -1.67
and an IQ of 130 corresponds with a z score of 2.00.
We can read the value for -1.67 by remembering that the normal
distribution is symmetric and then reading the value of .4525 off the table.
For 2.00 we find .4772. The probability of an IQ between 75 and 130
is the same as the probability of an IQ between 75 and 100 plus the
probability of an IQ between 100 and 130 or between 100 and 125 (75) plus
the probability of an IQ between 100 and 130 or .4525+.4772=.9297.
Including a sketch like in those given above is always appropriate.
In addition to being able to find the percentile of a score by finding its z-score, reading the area under the table, adding .5, and multiplying by 100, we can use the z-score table to find percentile rank for a given score. Since z-score tables are typically abbreviated, there are some tricks to the trade. Also, the algebra to transform the z-score equation (see below) often slows students down.
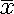 .
.
| BACK | HOMEWORK | ACTIVITY | CONTINUE |
|---|