Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
In the beginning God… Genesis 1:1 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.5
There is a legend that claims the Cartesian coordinate system was discovered when René Descartes was sick in bed. As he was staring up at the ceiling, he saw a fly. He wondered how he could describe the fly's position on the ceiling. If one corner of the room was taken as a reference point or origin, the fly's position could be described as the number of tiles horizontally from the origin followed by the number of tiles vertically from the origin. These two numbers are the coordinates of the fly's position. René Descartes first published the coordinate system that bears his name in 1637. It is sometimes called the rectangular coordinate system because the grid is made of squares.
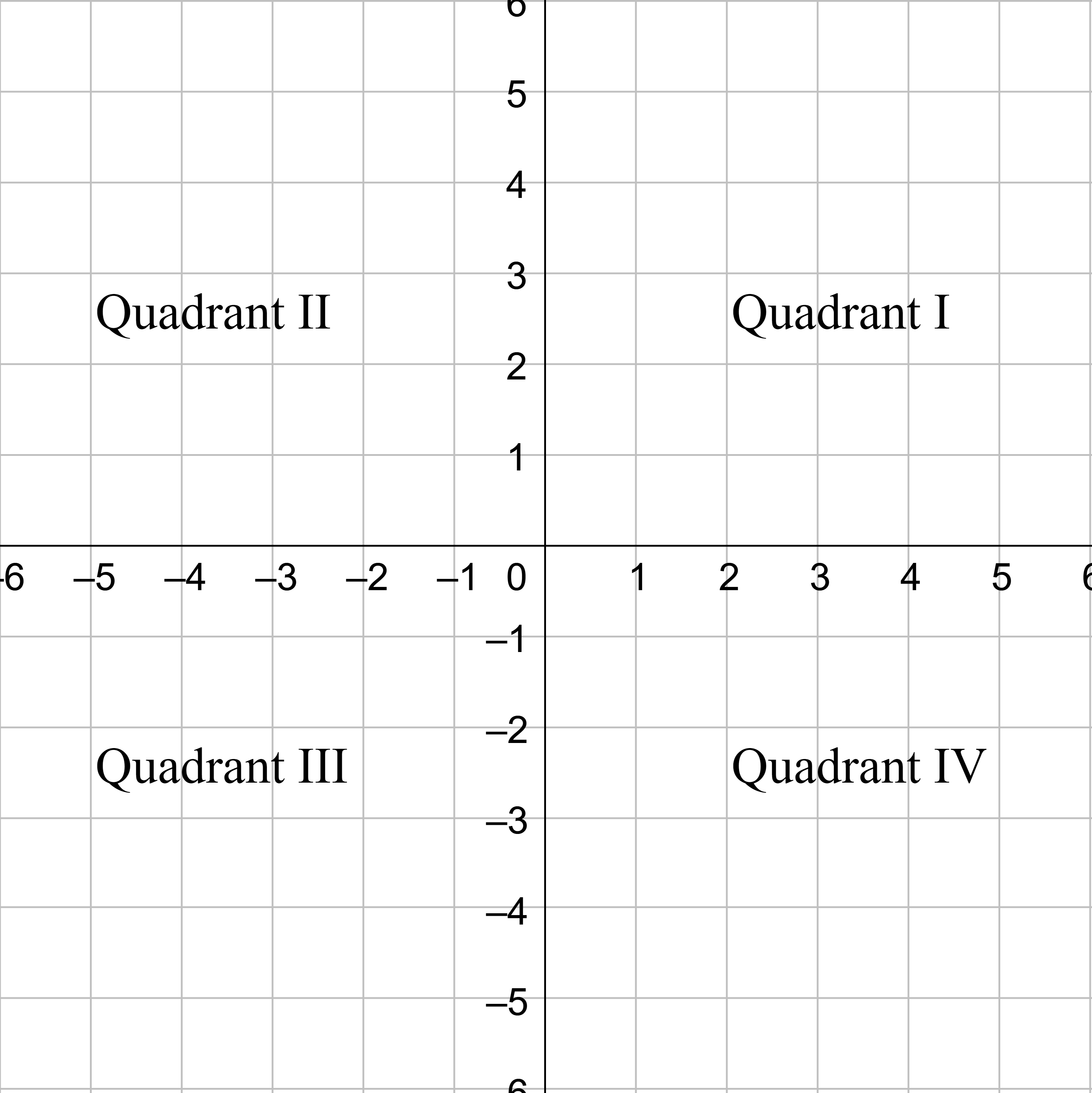
The Cartesian, or rectangular, coordinate system consists of a horizontal x-axis and a vertical y-axis. The point where the axes cross is called the origin. Any point can be described as the distance it is from the origin along the x-axis and along the y-axis and is written as (x, y). Positive x is to the right and positive y is up. Negative x is to the left and negative y is down. The location of a point is called its coordinate.
The horizontal x-axis and the vertical y-axis divide the plane into four quadrants which are numbered counterclockwise from the top right.
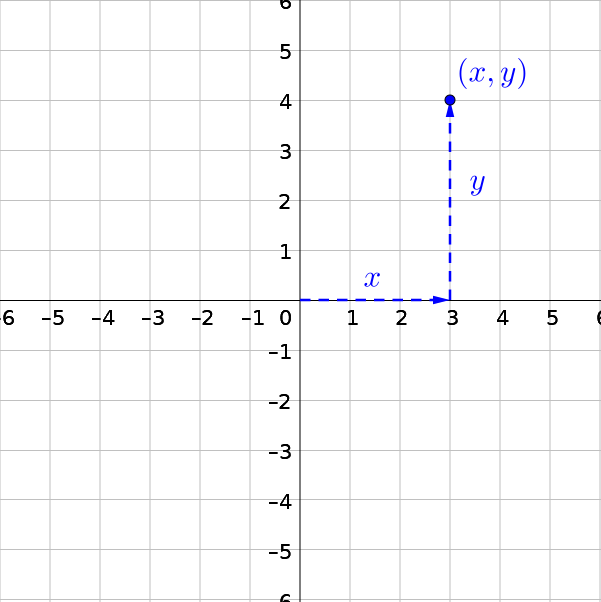
Given the point (x, y)
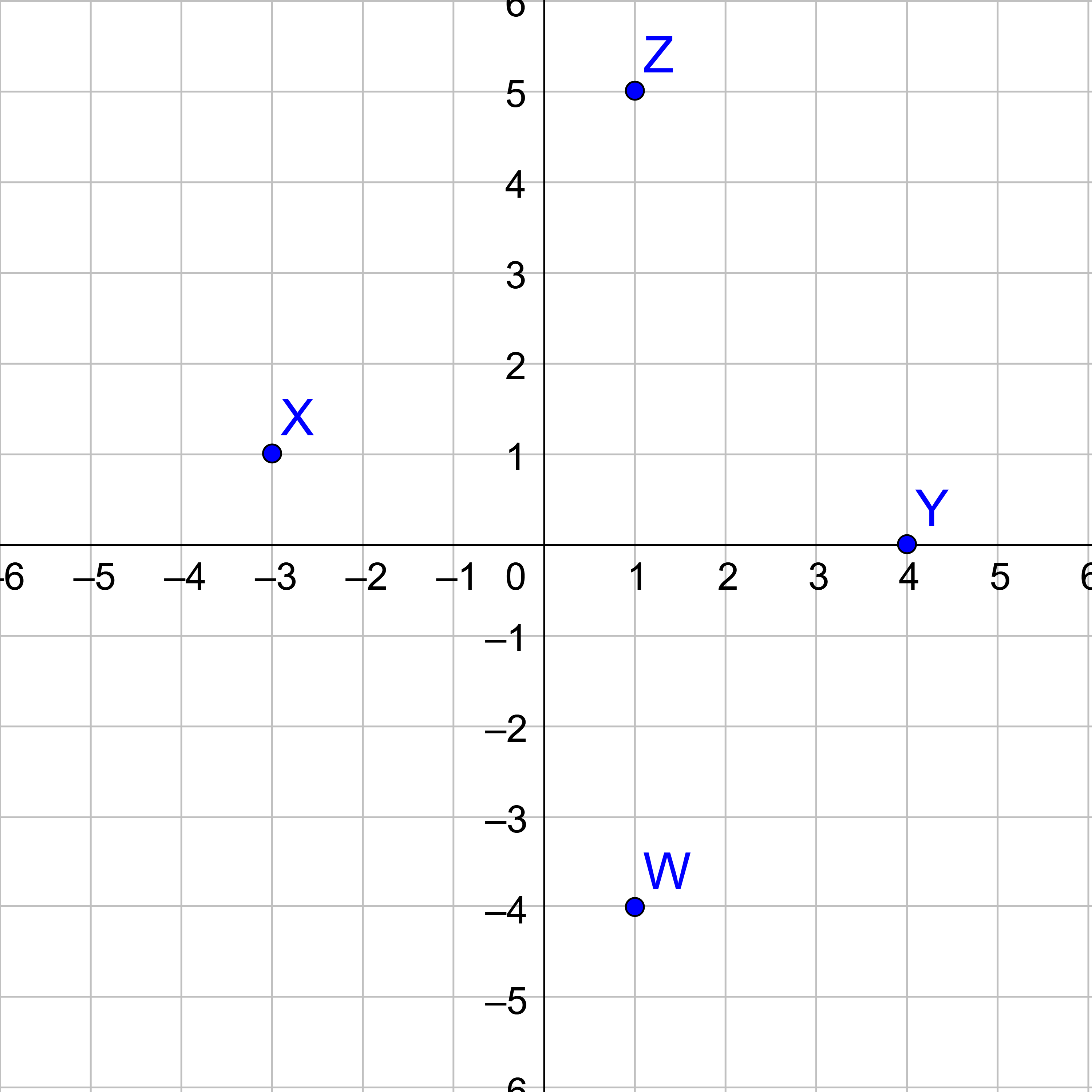
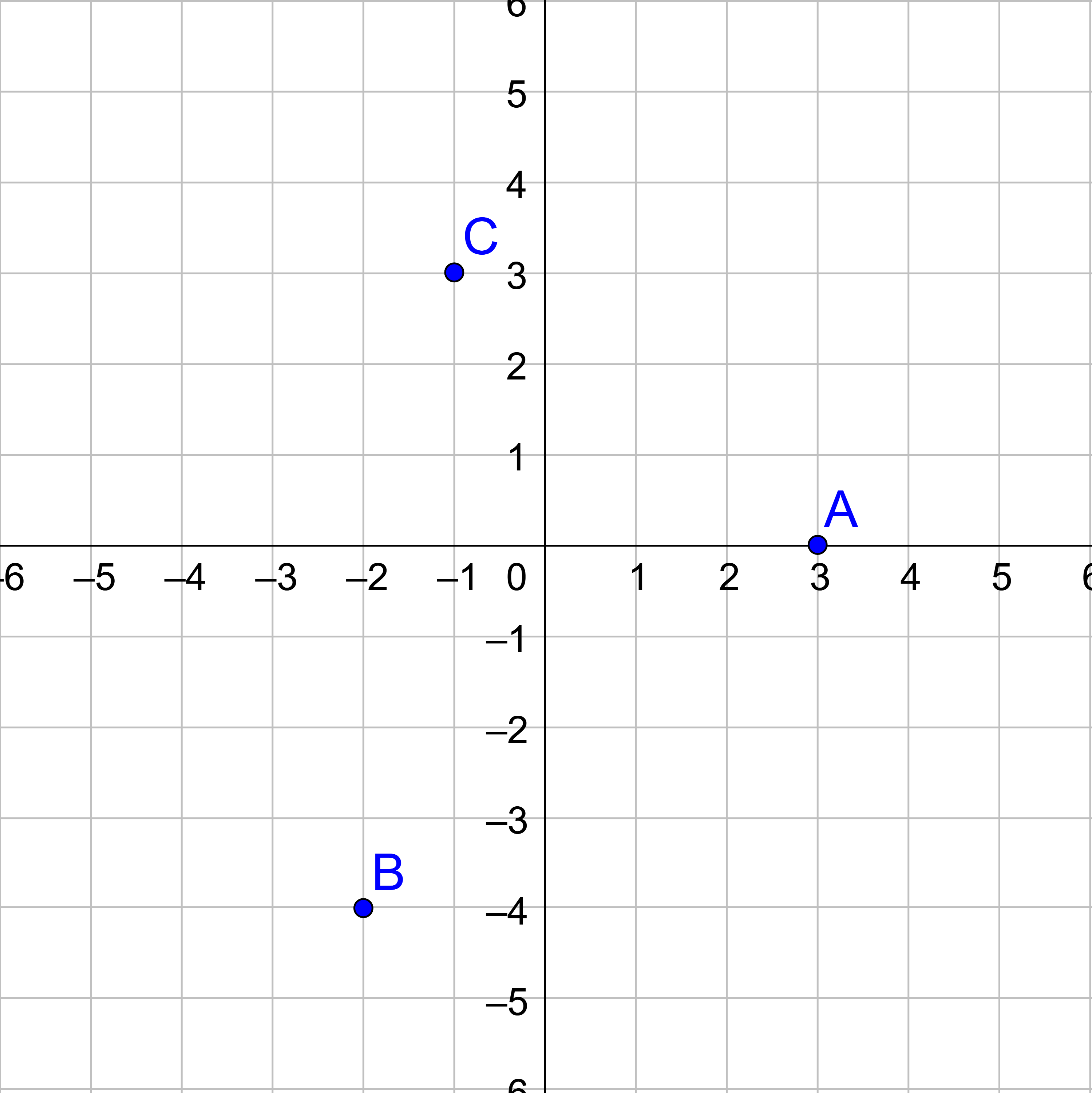
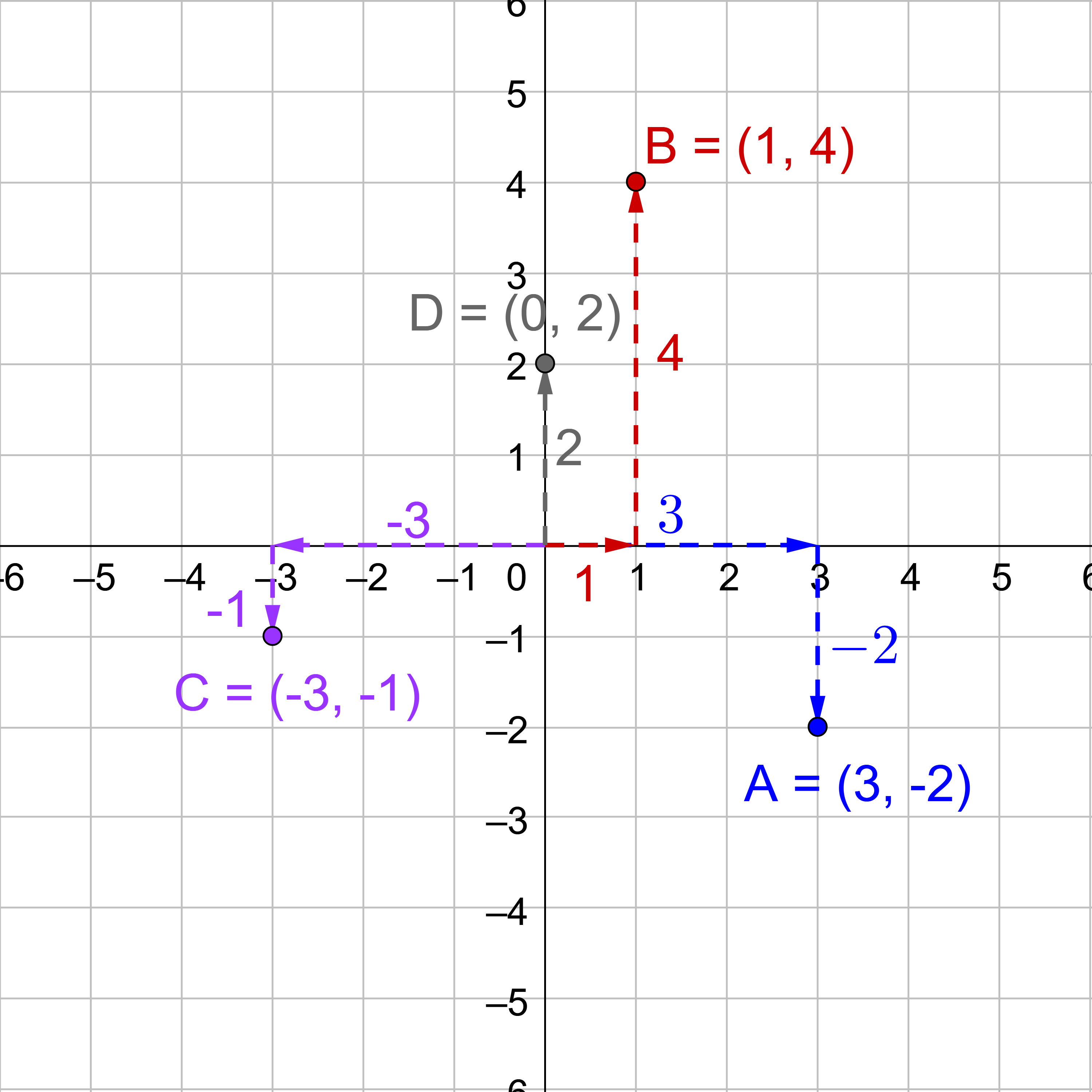
Plot the points A(3, −2), B(1, 4), C(−3, −1), D(0, 2).
Solution
The first number is the x and indicates how far right to move from the origin. The second number is the y and indicates how far up to move from the origin.
Figure 4 illustrates how to graph the points. The final graph would not have the arrows; it would only have the points.
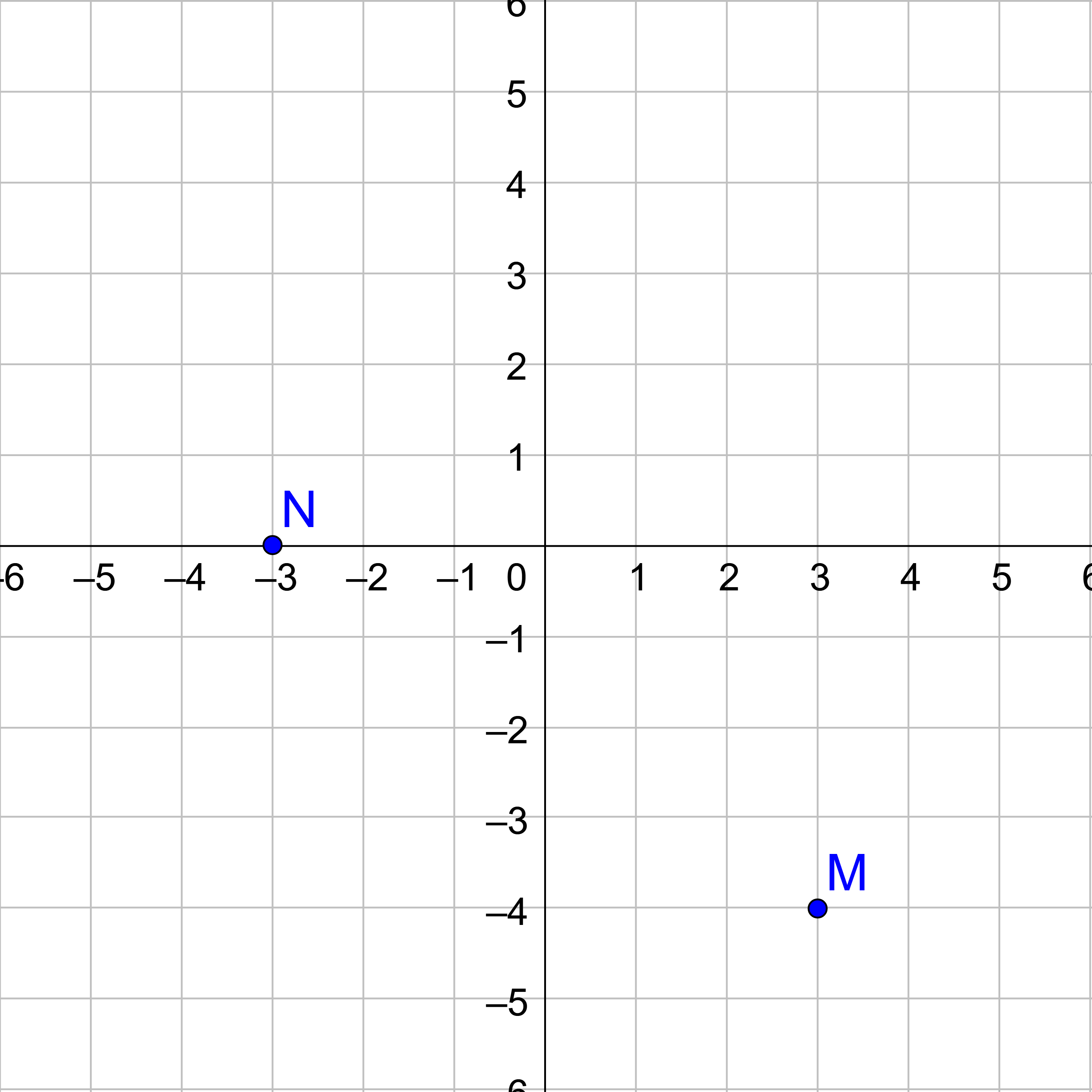
Plot the points M(3, −4) and N(−3, 0).
Answers
Now that points can located on the Cartesian plane, it might be nice to know how far apart they are. A right triangle can be created by drawing a segment between the two points. Then draw a the horizontal and vertical distances. The horizontal distance is found be subtracting the x-values of the points, Δx = x2 − x1, and the vertical distance is found by subtracting the y-values of the points, Δy = y2 − y1. The distance between the two points is the length of the hypotenuse of the right triangle and can be found using the Pythagorean Theorem.
$$ d^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2 $$
$$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$
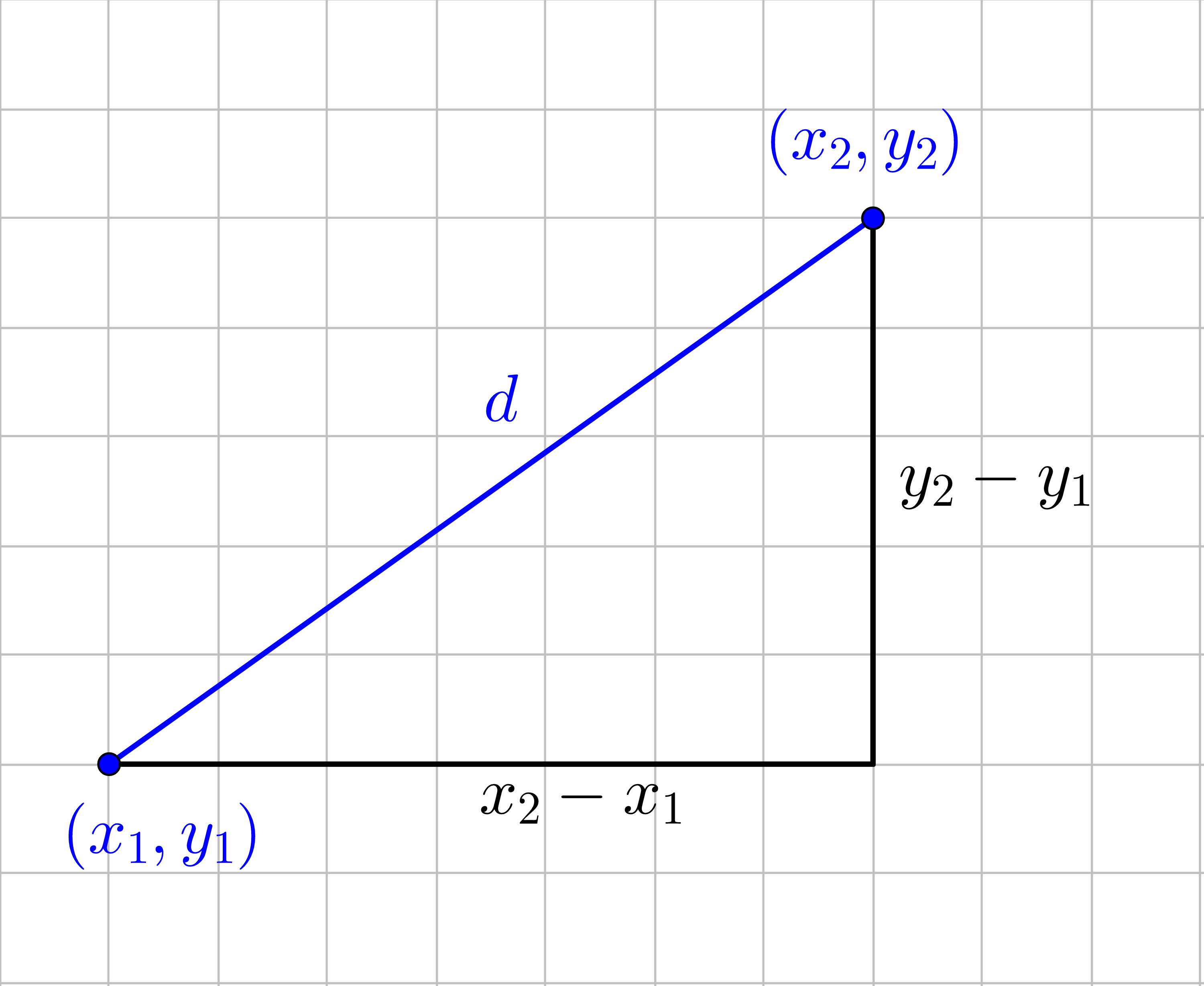
The distance, d, between two points (x1, y1) and (x2, y2) is
$$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$
Find the distance between W(−5, 8) and E(1, −4).
Solution
Fill in the distance formula using
W(−5, 8) = (x1, y1) and E(1, −4) = (x2, y2)
$$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$
$$ d = \sqrt{(1 - (-5))^2 + (-4 - 8)^2} $$
$$ d = \sqrt{180} $$
$$ d = \sqrt{(36)(5)} $$
$$ d = 6\sqrt{5} $$
Find the distance between H(3, 5) and I(−1, 3).
Answer
\(2\sqrt{5}\)
Find the missing coordinate given the distance between the points (2, 4) and (−1, y) is \(3\sqrt{2}\).
Solution
Start by filling in the points and distance into the distance formula.
$$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$
$$ 3\sqrt{2} = \sqrt{(-1 - 2)^2 + (y - 4)^2} $$
Simplify the first group.
$$ 3\sqrt{2} = \sqrt{\color{red}{9} + (y - 4)^2} $$
Square both sides.
$$ \color{red}{18} = 9 + (y - 4)^2 $$
Finish solving for y.
$$ 9 = (y - 4)^2 $$
Remember to use a ± when you take a square root while solving an equation.
$$ ±3 = y - 4 $$
$$ 4 ± 3 = y $$
$$ y = 1, 7 $$
Find the missing coordinate given the distance between the points (−1, 6) and (x, 7) is \(\sqrt{17}\).
Answer
x = −5, 3
A convenient result of the way the Cartesian coordinate system works, is that the x and y directions are completely independent from each other. Motion in the x does not affect motion in the y. This allows to calculations to be done simply by just thinking about the x and y separately.
A potentially useful thing to find on the Cartesian plane is to find the point halfway between two other points. This is called the midpoint. Since the midpoint is the middle, it can be found using the arithmetic mean or average. Because of the independence of the x and y, the average can be taken in both directions separately.
$$ Midpoint = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right) $$
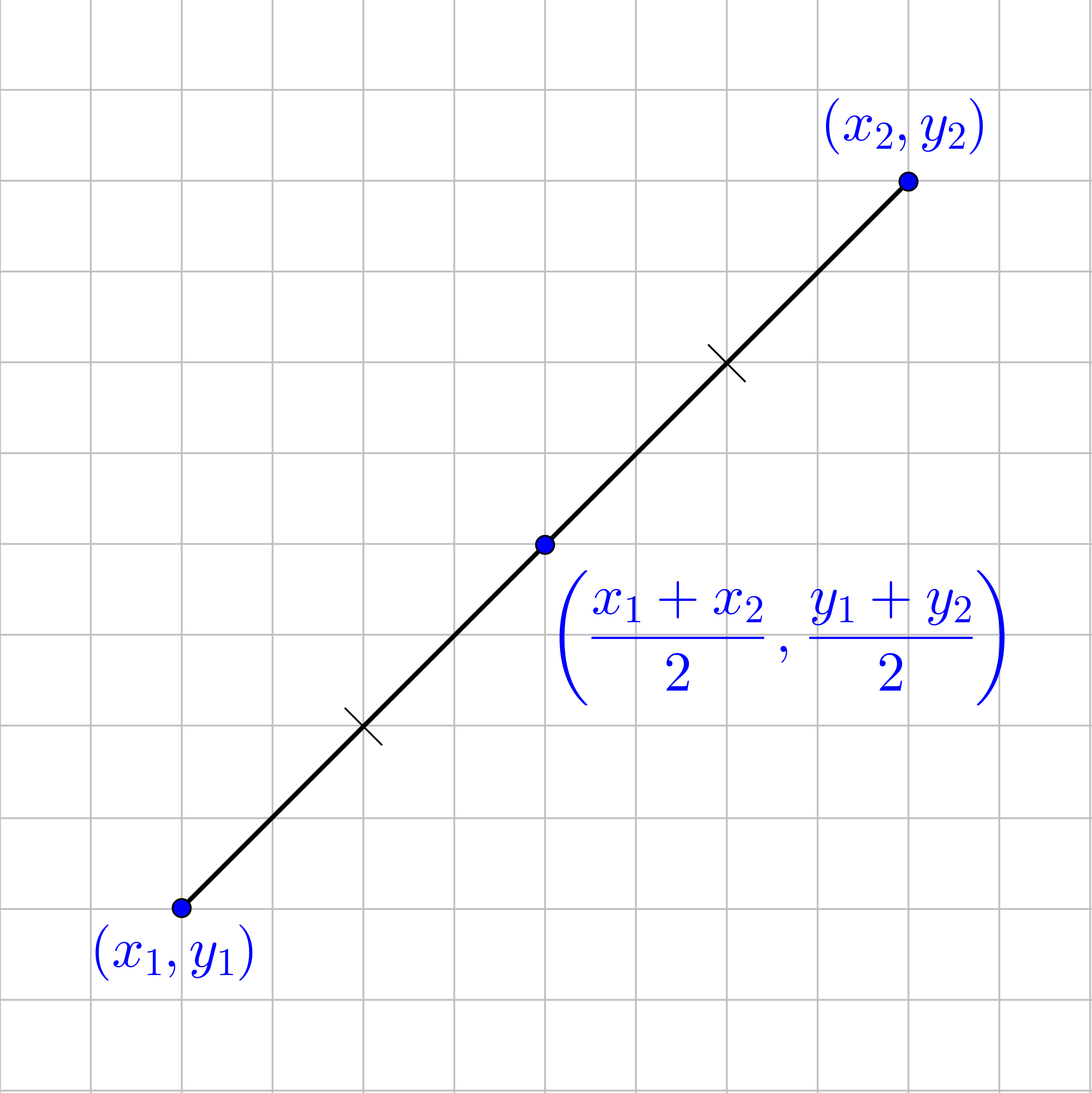
The midpoint between two points (x1, y1) and (x2, y2) is
$$ Midpoint = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right) $$
Find the midpoint between R(2, 4) and W(−3, 1).
Solution
Fill in the midpoint formula using
R(2, 4) = (x1, y1) and W(−3, 1) = (x2, y2)
$$ Midpoint = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right) $$
$$ Midpoint = \left(\frac{2 + (-3)}{2}, \frac{4 + 1}{2}\right) $$
$$ Midpoint = \left(-\frac{1}{2}, \frac{5}{2}\right) $$
Find the midpoint between H(3, 5) and I(−1, 3).
Answer
(1, 4)
Find the missing endpoint given one endpoint is (2, −1) and the midpoint is (5, 6).
Solution
Fill in the given endpoint for (x1, y1) and the midpoint into the midpoint formula.
$$ Midpoint = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right) $$
$$ (5, 6) = \left(\frac{2 + x_2}{2}, \frac{-1 + y_2}{2}\right) $$
Because the x and y are independent, they can be solved separately. Make an equation out of just the x-coordinates and solve it.
$$ 5 = \frac{2 + x_2}{2} $$
$$ 10 = 2 + x_2 $$
$$ x_2 = 8 $$
Repeat for the y-coordinate.
$$ 6 = \frac{-1 + y_2}{2} $$
$$ 12 = -1 + y_2 $$
$$ y_2 = 13 $$
The answer is (x2, y2) which is (8, 13).
Find the missing endpoint given one endpoint is (−3, 0) and the midpoint is (1, −2).
Answer
(5, −4)
Given the point (x, y)
The distance, d, between two points (x1, y1) and (x2, y2) is
$$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$
The midpoint between two points (x1, y1) and (x2, y2) is
$$ Midpoint = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right) $$
Helpful videos about this lesson.
