Precalculus by Richard Wright
Precalculus by Richard Wright
Be strong and take heart, all you who hope in the Lord. Psalms 31:24 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.6.4

Vending machines take an input, money, and give an output, food. If the machine functions properly, it will dispense the desired item. This lesson explores the idea of a function.
A relation is a set of ordered pairs. The set of the first number of the pairs is the domain, or input, and the set of the second number of the pairs is the range, or output. For example, consider a vending machine where there are no choice buttons. It works by inserting the correct amount of money, and the machine automatically dispenses the food. The following ordered pairs could represent the price and food.
{(0.50, Bubble Gum), (0.75, Potato Chips), (1.00, Candy)}
The domain is {0.50, 0.75, 1.00}. The range is {Bubble Gum, Potato Chips, Candy}.
The values in the domain are known as the input values or independent variable, and is often labeled x. The values in the range are known as the output values or dependent variable, and is often labeled y.
A function f is a relation that assigns a single value in the range to each value in the domain. That means no x-values are repeated with different y-values. In the example above, each number in the domain is paired with exactly one number in the range making it a function. Think of it this way. Kim wants some candy, so she inserts $1.00 and the machine gives her candy. Kim says, "The machine functions."
Now consider that the price of potato chips has increased and now cost $1.00. This changes the relation of the vending machine.
{(0.50, Bubble Gum), (1.00, Potato Chips), (1.00, Candy)}
Karl walks by the machine and decides he wants some salty potato chips. He does not want the sweet candy. He inserts the $1.00 and the machine now has a choice. The input of $1.00 is paired with two different outputs: potato chips and candy. Remember there are no buttons to push, the machine automatically dispenses the food based on the input. The machine randomly chooses candy. Karl is upset because he did not get what he wanted. Karl says, "The machine does not function!" This new relation is not a function. Different inputs can go to the same output, but the same input cannot go to different outputs.
Figure 2 compares relations that are functions and not functions.
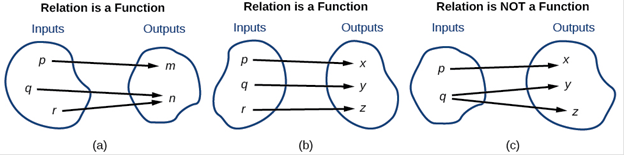
A function is a relation with each possible input value paired to exactly one output value.
The input values make up the domain, and the output values make up the range.
Determine whether the following relations are functions. If they are not, explain why.
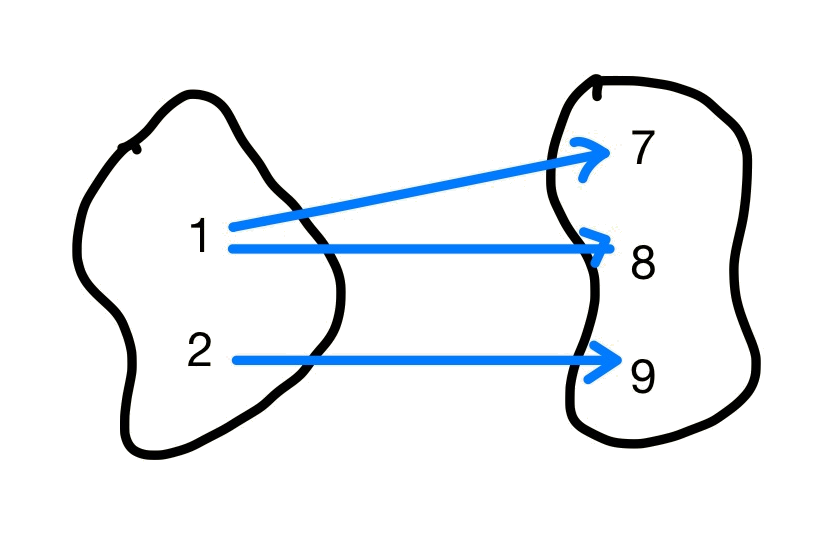
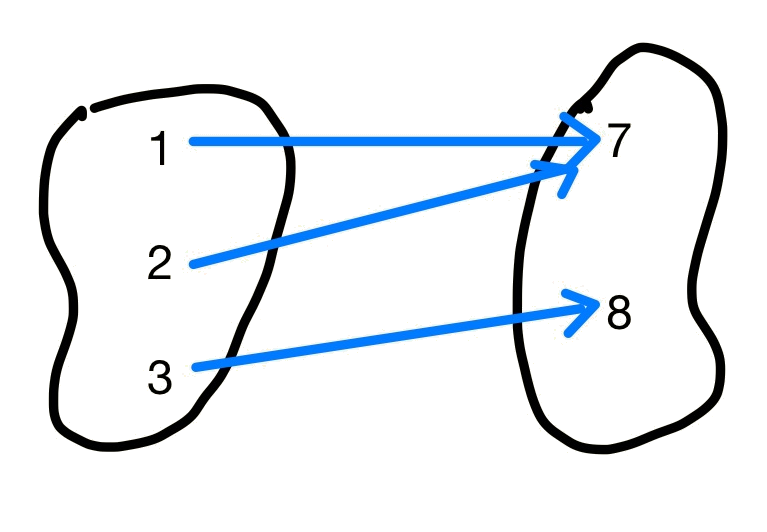
Solution
Functions are very important in math because most uses of math require only one output per one input. Often functions are represented as equations, but having a list of several equations all starting y = could be confusing when identifying a certain function. Thus, it is nice to give functions names. Function notation names functions and its variable. It replaces "y =" in the equation. For example, using f(x) = says the name of the function is f and the independent variable is x. A function about the height of a tree with time might be h(t) where the function is named h for height and the independent variable is t for time. The name h(t) is read as "h is a function of t".
If the function is evaluated at some value, then that number is substituted for the variable in the name. For example if function f(x) is evaluated at x = 2, then the name is written f(2). Remember this indicates that 2 is the input of the function; it is not multiplication.
The notation f(x) defines a function named f.
Use function notation to represent a function whose input is the day of the week and output is the number of days until the weekend.
Solution
The function gives the number of days until the weekend, so maybe call it w. The input is the day of the week, so call it d. The function would be w(d). An example would be input of Wednesday and output of 3 days: w(Wednesday) = 3 days until the weekend.
Use function notation to represent a function whose input is the age of a child, a, and the output is its height, h.
Answer
h(a)
A function N(m) gives the number of geese, N, in a park's pond in month m as a number. What does N(7) = 74 represent?
Solution
The input of the function is the month as a number. The input of N(7) = 74 is 7 and represents July. The output is the number of geese in the park's pond and is 74. Thus, the function is saying there are 74 geese on the pond in July.
A function B(d) gives the number of days of good weather remaining to visit the beach, B, for a given day in September, d. What does B(10) = 8 mean?
Answer
There are 8 more good beach days after September 10.
After understanding function notation, it is important to know how to evaluate function outputs. Remember that every input gives exactly one output. Other times the output is known and the input is desired. This is solving and can produce more than one solution since more than one input can give the same output.
When the function is given as a formula or equation, evaluating is done by substituting the input value into the equation and then simplifying.
Given f(x) = x2 − 2x + 1, evaluate
Solution
Replace the x in the function with each given value.
Substitute the input value, 2, for x and simplify.
f(x) = x2 − 2x + 1
f(2) = 22 − 2(2) + 1
f(2) = 1
Substitute the input value, a, for x and simplify.
f(x) = x2 − 2x + 1
f(a) = a2 − 2a + 1
Substitute the input value, a + h, for x and simplify.
f(x) = x2 − 2x + 1
f(a + h) = (a + h)2 − 2(a + h) + 1
f(a + h) = a2 + 2ah + h2 − 2a − 2h + 1
This expression has two instances of function notation. The first one, f(a + h) was the answer for part c. The second one, f(a) was the answer for part b. Substitute these into the expression and simplify.
$$ \frac{f(a + h) - f(a)}{h} $$
$$ \frac{(a^2 + 2ah + h^2 - 2a - 2h + 1) - (a^2 - 2a + 1)}{h} $$
Collect like terms. Notice all terms without h happen to cancel out.
$$ \frac{2ah + h^2 - 2h}{h} $$
Factor h in the numerator.
$$ \frac{h(2a + h - 2)}{h} $$
Cancel the h.
2a + h − 2
Given the function \(I(q) = \frac{q}{200}\), evaluate I(400).
Solution
To evaluate I(400), substitute the value 400 for the input variable q in the function.
$$ I(q) = \frac{q}{200} $$
$$ I(400) = \frac{400}{200} $$
I(400) = 2
Given the function f(x) = −2x + 3, evaluate f(7).
Answer
f(7) = −11
It is also possible to find input and output values from a graph. If given an input value, find it on the horizontal axis. Then move up until reaching the graph. Next, move horizontally to the vertical axis. Finally, read the output value from the scale on the axis.
If given an output value, find it on the vertical axis. Then move horizontally until reaching the graph. Next, move vertically to the horizontal axis. Finally, read the input value from the scale on the axis.
To evaluate a function for a given x-value
To solve a function for a given y-value
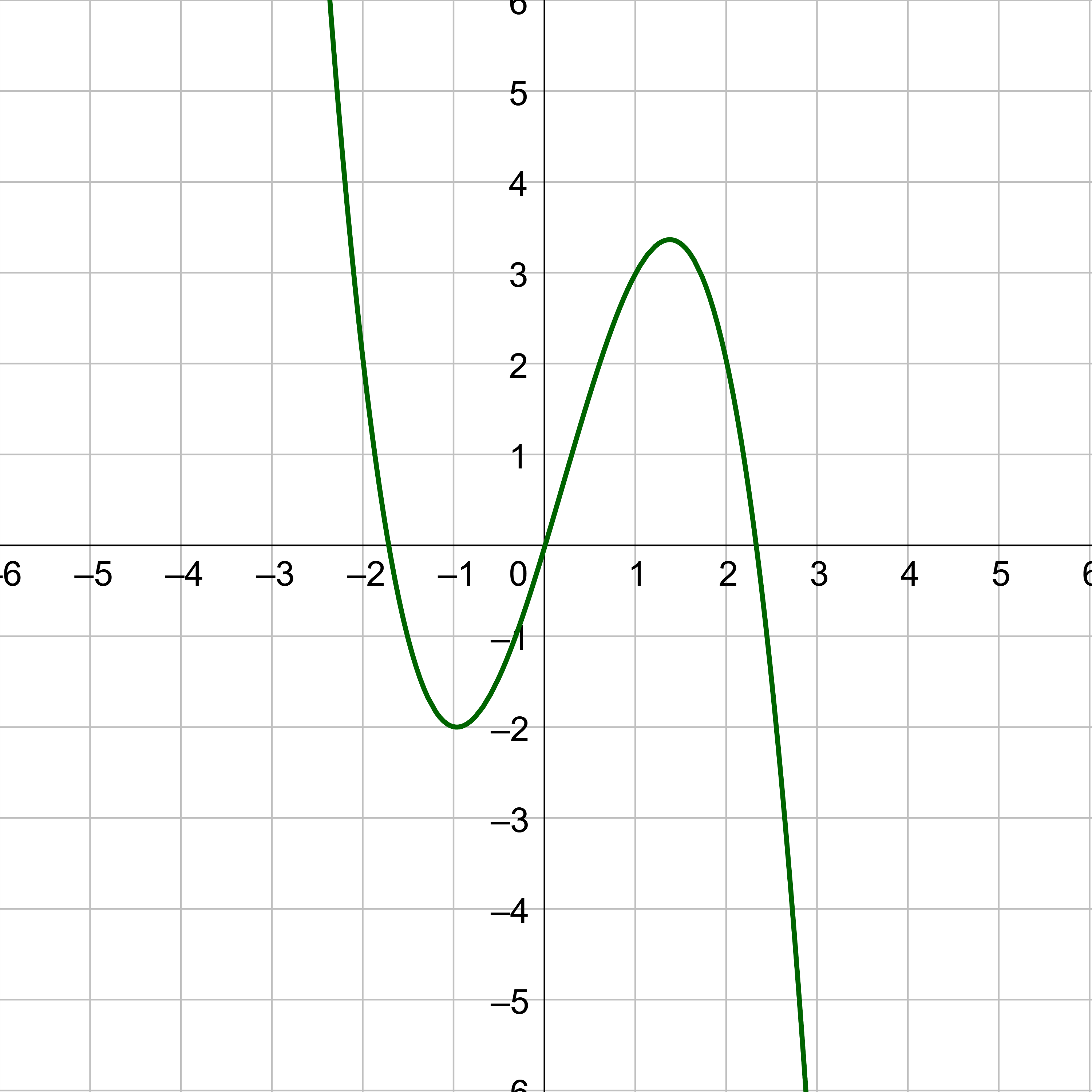
Given the graph in figure 3,
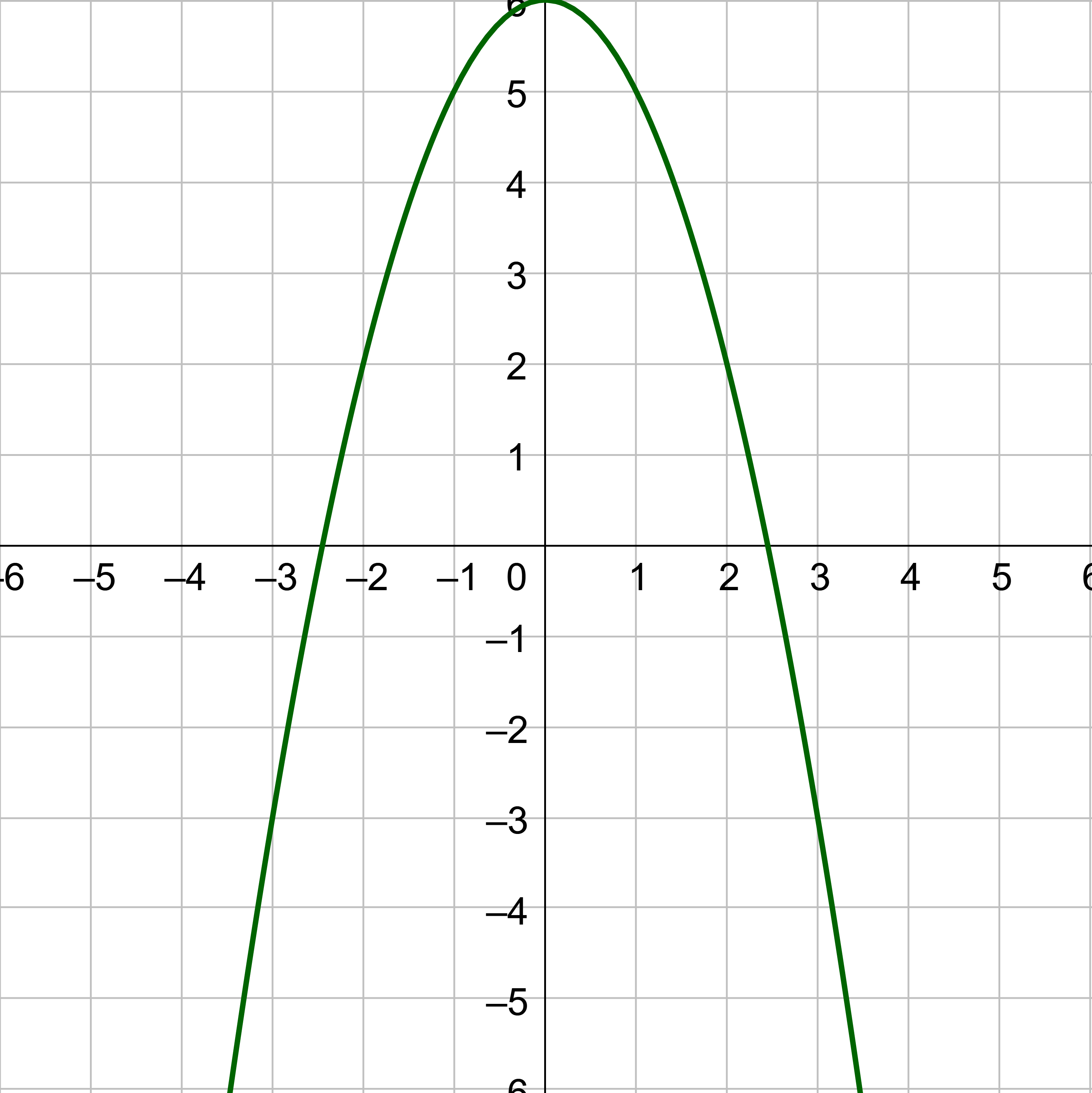
Solution
To evaluate f(1),
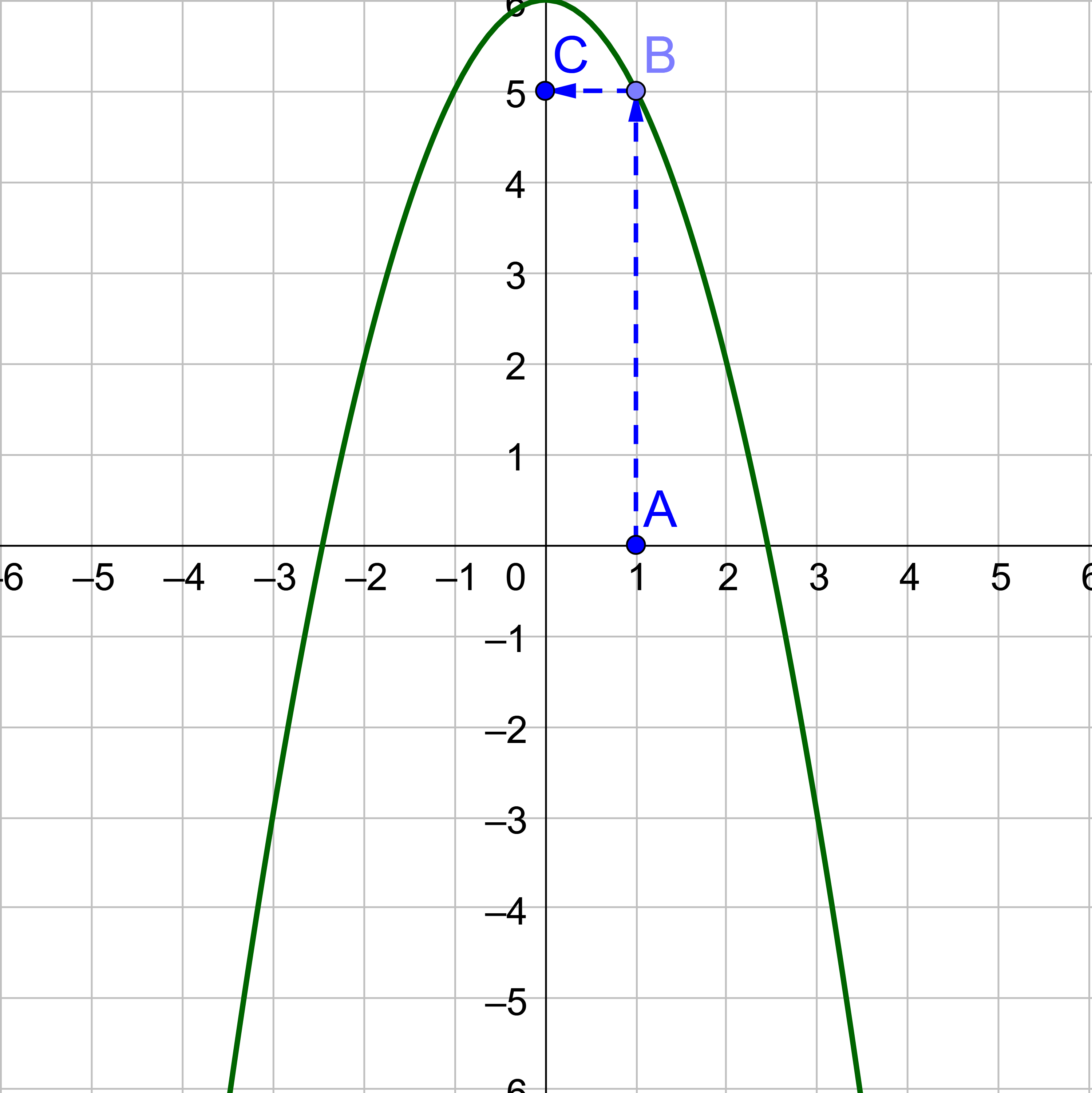
f(1) = 5
To solve f(x) = 2,
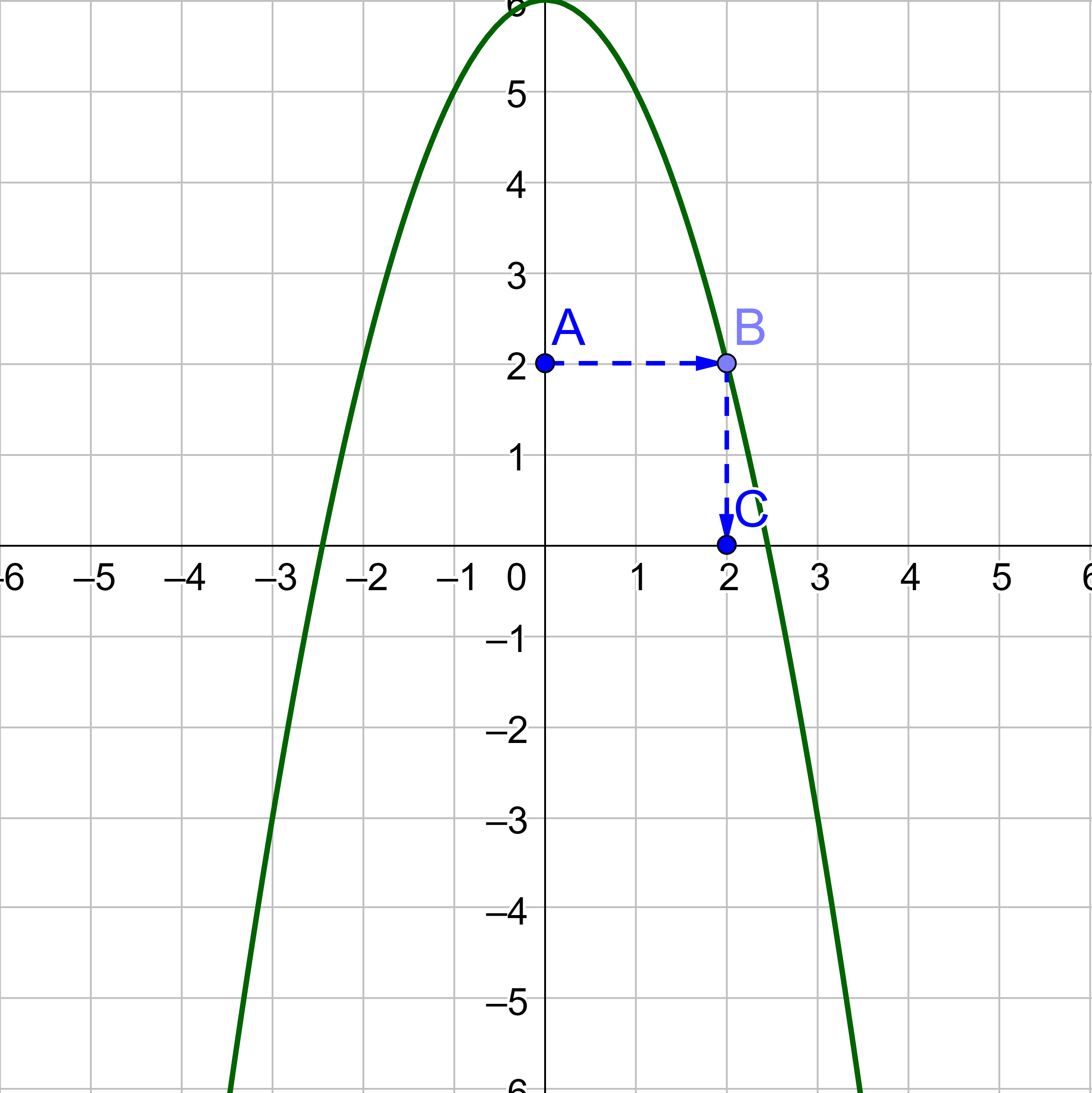
Notice there is also an answer on the left side of the graph.
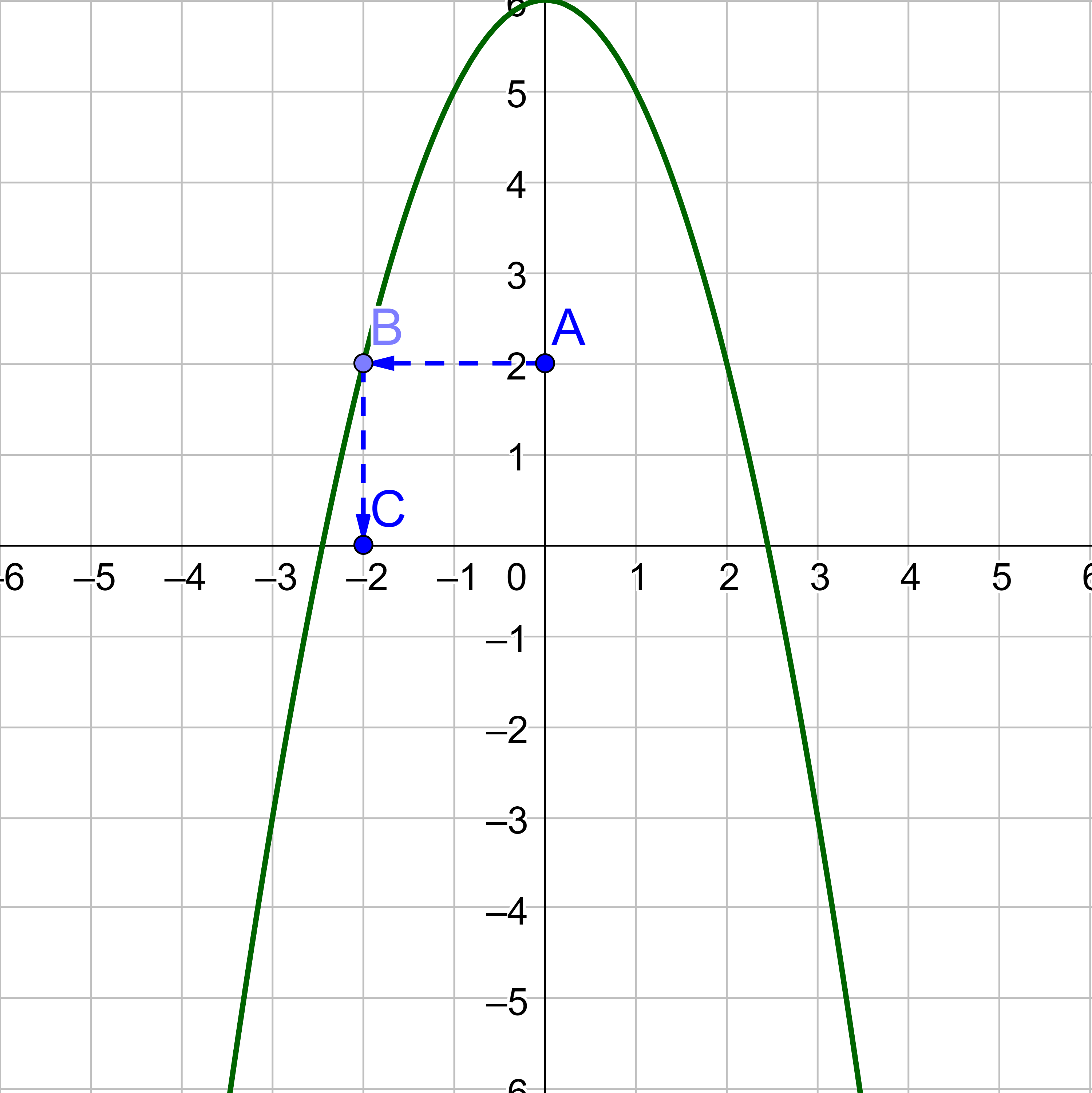
f(−2) = 2 and f(2) = 2
The domain of a function is all the inputs, or x-values, that give outputs, or y-values.
Find the domain of the following function: {(1, 15), (2, 10), (3, 5), (4, 10), (5, 15)}.
Solution
The domain is the input values which are the first number of each ordered pair.
Domain = {1, 2, 3, 4, 5}
Interval form of a set is given by two numbers and brackets, such as (lower limit, upper limit].
Examples of interval notation are
Find the domain of the function f(x) = x2 + 2.
Solution
The input value, x, is squared and then the result is increased by two. Any real number may be squared and then be increased by two, so there are no restrictions on the domain of this function. The domain is all real numbers.
In interval form, the domain of f is (−∞, ∞).
Find the domain of the function \(g(x) = \frac{x+2}{x-3}\).
Solution
The input value is x. The function is undefined when it is divided by 0. Find the excluded values of x by setting the denominator equal to 0 and solving for x.
x − 3 = 0
x = 3
Now, exclude that value, 3, from the domain. The domain is all real numbers except 3. This can be written as x ≠ 3. This can also be written as x < 3 or x > 3. These can be combined using the union symbol, ∪.
In interval form, the domain of g is (−∞, 2) ∪ (2, ∞).
Find the domain of the function \(h(x) = \sqrt{x + 6}\).
Solution
The input variable is x. When there is an even root in the equation, all negative numbers are excluded from the radicand because even roots of negative number produce unreal results.
Set the radicand greater than or equal to zero and solve for x.
x + 6 ≥ 0
x ≥ −6
The domain is all numbers greater than or equal to −6.
In interval form, the domain of h is [−6, ∞).
Find the domain of \(f(x) = \frac{2}{\sqrt{x}}\).
Answer
(0, ∞)
Some functions are made up of several different equations or pieces. A piecewise function is a function in which more than one formula is used to define the output over different pieces of the domain.
Piecewise functions are used to describe situations where the rule or relation changes as the input crosses certain boundaries. For example, the United States Postal Service uses a piecewise function to determine the cost to mail a first class letter. The price is $0.55 if the weight is ≤ 1 ounce. The price is $0.75 for weights 1 < w ≤ 2 ounces. The cost goes up 20 cents for every partial ounce.
Piecewise functions are written like this:
$$ f(x) = \left\{\begin{align} \text{formula 1}, \text{if domain 1} \\ \text{formula 2}, \text{if domain 2} \\ \text{formula 3}, \text{if domain 3} \end{align}\right. $$
For the Postal Service above, the postal rates use the piecewise formula
$$ p(x) = \left\{\begin{align} 0.55&, \text{if } x ≤ 1 \\ 0.75&, \text{if } 1 < x ≤ 2 \\ 0.95&, \text{if } 2 < x ≤ 3 \\ 1.15&, \text{if } 3 < x ≤ 4 \\ \vdots \end{align}\right. $$
A piecewise function is made up of several functions over defined intervals.
$$ f(x) = \left\{\begin{align} \text{formula 1}, \text{if domain 1} \\ \text{formula 2}, \text{if domain 2} \\ \text{formula 3}, \text{if domain 3} \end{align}\right. $$
A museum charges $5 per person for a guided tour with a group of 1 to 9 people or a fixed $50 fee for a group of 10 or more people. Write a function relating the number of people, n, to the cost, C.
Solution
Two different formulas are needed. For n-values less than 10, C = 5n. When n is 10 or greater, the cost is $50 or C = 50.
$$ C(n) = \left\{\begin{align} 5n&, \text{if } n < 10 \\ 50&, \text{if } n ≥ 10 \end{align}\right. $$
A cell phone company uses the function below to calculate the cost, C, in dollars for g gigabytes of data.
$$ C(g) = \left\{\begin{align} 50&, \text{if } g ≤ 5 \\ 50 + 10(g - 5)&, \text{if } g > 5 \end{align}\right. $$
Find the cost of using 3.5 gigabytes of data and the cost of using 8 gigabytes of data.
Solution
To find the cost of 3.5 gigabytes of data, determine which of the domains it fits in. In this case, 3.5 ≤ 5, so it is in the domain of the top equation. Substitute the 3.5 into the first equation to get the answer. Of course, the top equation is just the constant 50, so the result is 50.
C(3.5) = 50
The cost of 3.5 gigabytes of data is $50.
To find the cost of 8 gigabytes of data, determine which of the domains it fits in. In this case, 8 > 5, so it is in the domain of the bottom equation. Substitute the 8 into the bottom equation to get the answer.
C(g) = 50 + 10(g − 5)
C(8) = 50 + 10(8 − 5)
C(8) = 80
The cost of 8 gigabytes of data is $80.
Given \(g(x) = \left\{\begin{align} x^2&, \text{if } x < 2 \\ -x + 6&, \text{if } x ≥ 2 \end{align}\right.\), evaluate (a) g(2) and (b) g(5).
Answer
4; 1
A function is a relation with each possible input value paired to exactly one output value.
The input values make up the domain, and the output values make up the range.
The notation f(x) defines a function named f.
To evaluate a function for a given x-value
To solve a function for a given y-value
Interval form of a set is given by two numbers and brackets, such as (lower limit, upper limit].
Examples of interval notation are
A piecewise function is made up of several functions over defined intervals.
$$ f(x) = \left\{\begin{align} \text{formula 1}, \text{if domain 1} \\ \text{formula 2}, \text{if domain 2} \\ \text{formula 3}, \text{if domain 3} \end{align}\right. $$
Helpful videos about this lesson.