Precalculus by Richard Wright

Previous Lesson Table of Contents Next Lesson

Has this helped you?

This book is available
in print and ebook.


We love because he first loved us. 1 John 4:19 NIV

1-Review

Take this test as you would take a test in class. When you are finished, check your work against the answers.

  1. Plot the points (−5, 1) and (2, 6). Find the coordinates of the midpoint of the line segment joining the points and the distance between the points.
  2. Graph \(f(x) = \sqrt{x+3}\).
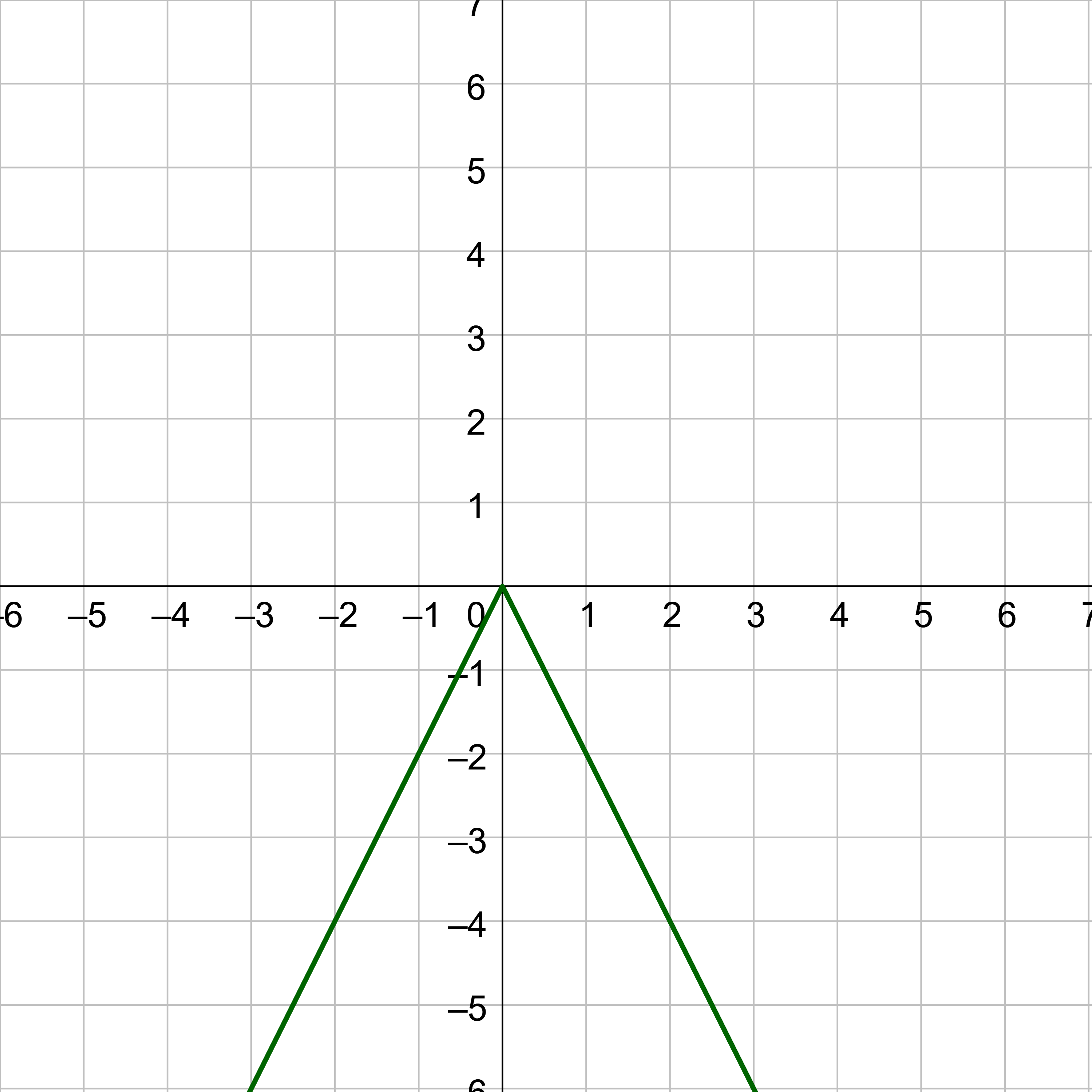
  3. Graph f(x) = −|2x|.
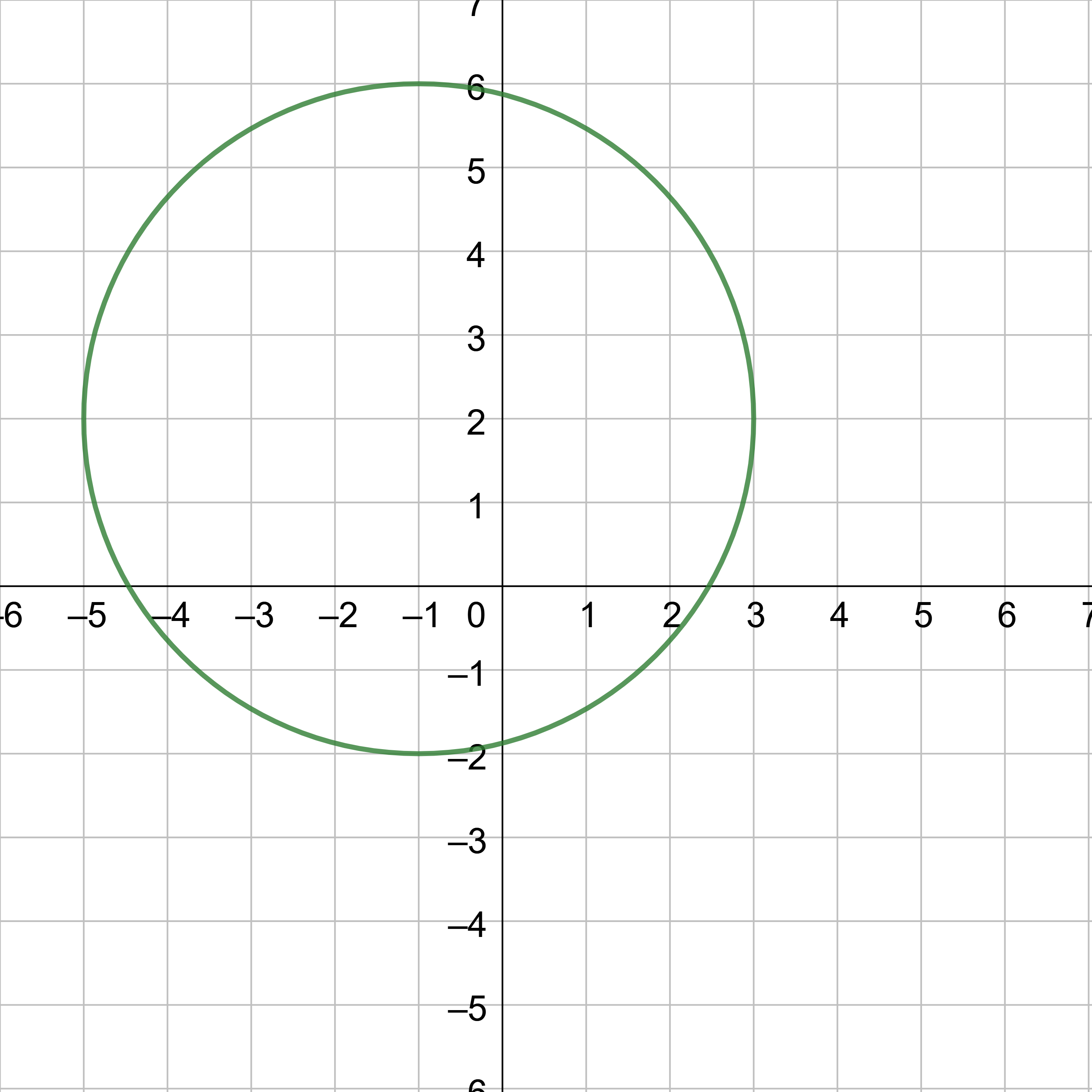
  4. Graph (x + 1)2 + (y − 2)2 = 16.
  5. Graph \(f(x) = \left\{\begin{align} \tfrac{1}{2}x^2, \text{ if }x ≤ 0 \\ -|x|, \text{ if } x > 0\end{align}\right.\).
  6. Find the equation of the line passing through (15, 20) and (17, −10).
  7. Find the equation of the line parallel to y = −2x − 1 and passing through (1, 3).
  8. If f(x) = 3x3 + |x|, find f(−2).
  9. If \(f(x) = \frac{x}{x-1}\), find f(x + 2).
  10. Find the domain of \(f(x) = \sqrt{2x-4}\).
  11. Find the zeros of f(x) = x2 − 4.
  12. Determine the intervals that f(x) = −|x + 4| is increasing and decreasing.
  13. Identify the parent function of \(f(x) = \frac{2}{(x+2)^2}\).
  14. Describe how the formula is a transformation of a parent function: g(x) = −|2x| + 3.
  15. Find the inverse of f(x) = (x − 2)2, x < 2.
  16. If y varies directly with x, and y = 4 when x = 3, find y when x = \(\frac{3}{5}\).
  17. Use f(x) = 2x − 1 and g(x) = 4x2 to solve the following problems.
  18. Find (gf)(x).
  19. Find (f ∘ g)(x).
  20. Find (g ∘ f)(x).
  21. For the following data set, draw a scatter plot and then use technology to find the equation of the best fitting line.
    246810
    1013151922

Answers

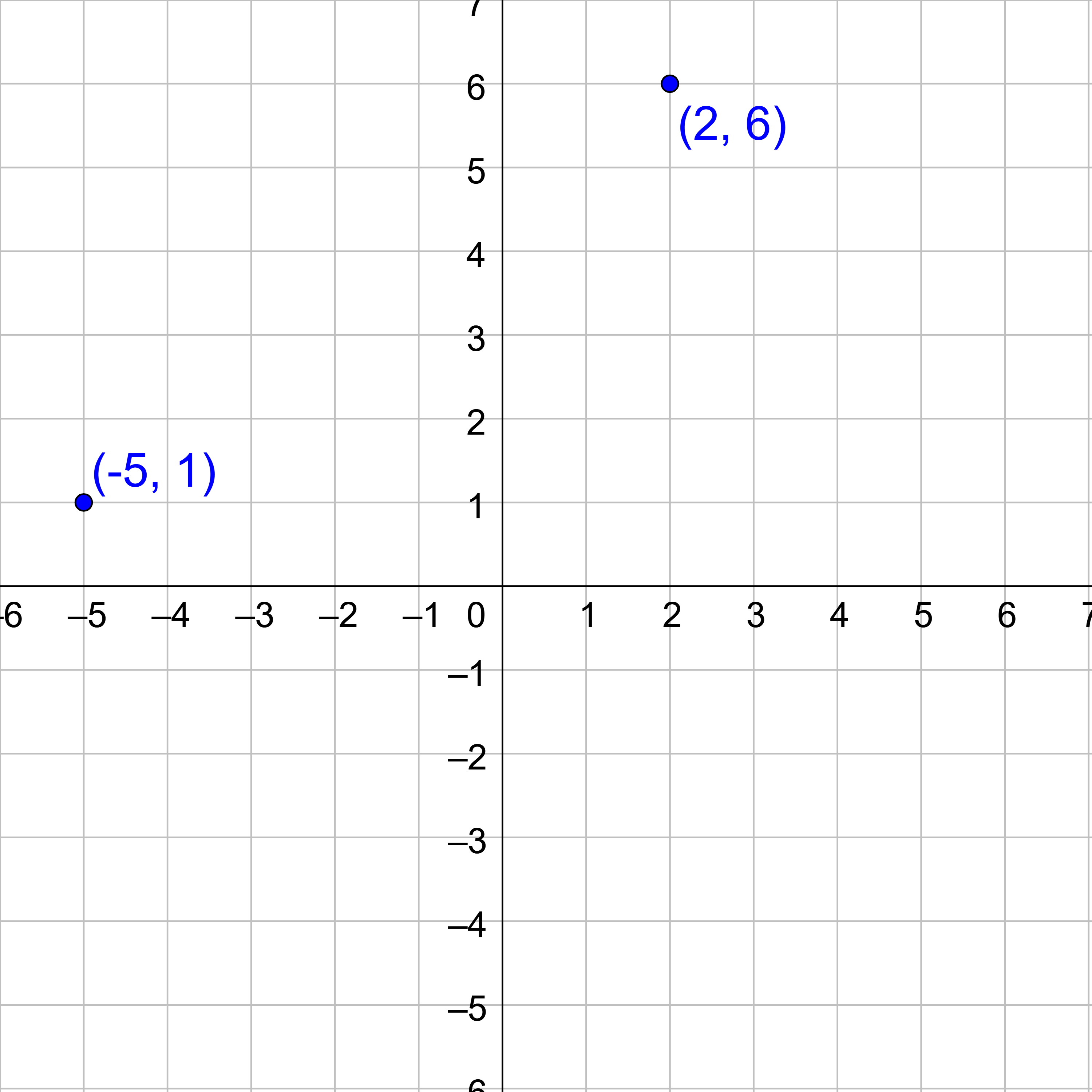  1. \(\left(-\frac{3}{2}, \frac{7}{2}\right)\); \(\sqrt{74}\)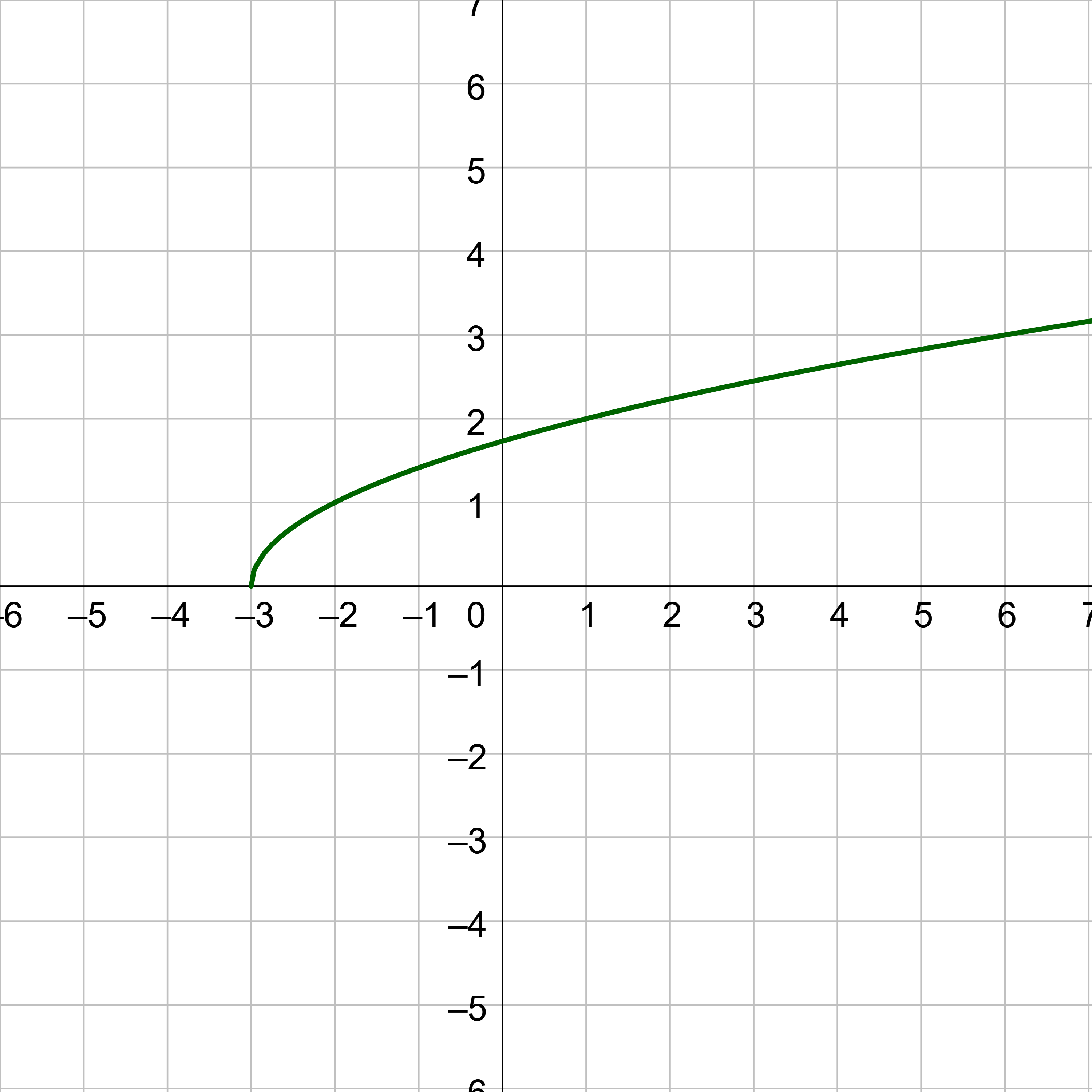
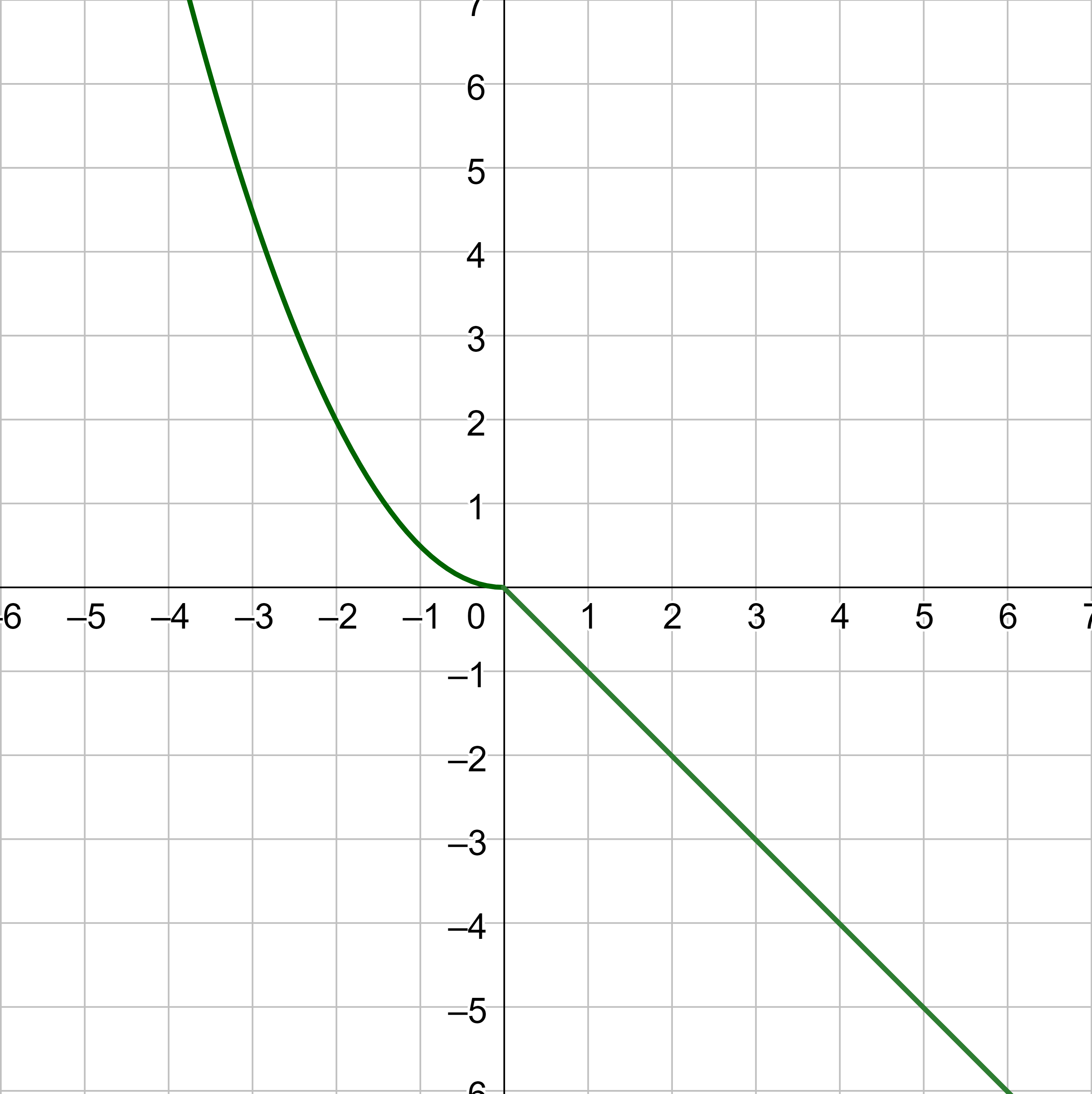
  6. y = −15x + 245
  7. y = −2x + 5
  8. −22
  9. \(\frac{x+2}{x+1}\)
  10. [2, ∞)
  11. −2, 2
  12. Increasing: (−∞, −4); Decreasing: (−4, ∞)
  13. Reciprocal squared function
  14. Reflected over the x-axis, Horizontal contraction by a factor of \(\frac{1}{2}\), Vertical shift of 3
  15. \(f^{-1}(x) = -\sqrt{x} + 2\)
  16. \(y = \frac{4}{5}\)
  17. 8x3 − 4x2
  18. 8x2 − 1
  19. 16x2 − 16x + 4
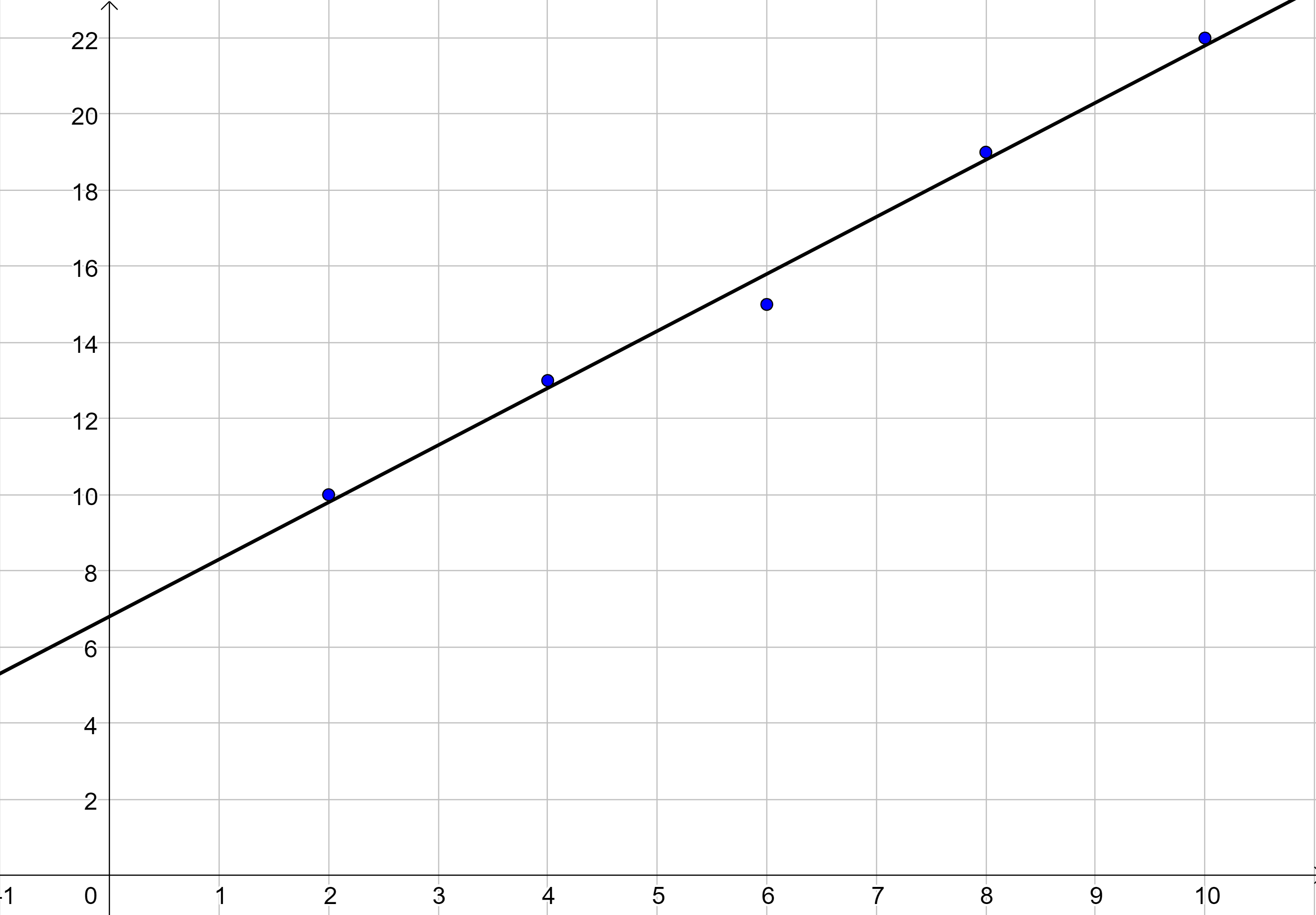  20. ; y = 1.5x + 6.8