Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Even though I walk through the darkest valley, I will fear no evil, for you are with me; your rod and your staff, they comfort me. Psalms 23:4 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.5.6
Mathematics continually builds on itself. Young children are taught counting numbers, then the knowledge expands to include negative numbers. Next fractions and rational numbers fill the spaces between the integers. Finally, students learn about irrational numbers such as π and \(\sqrt{2}\). Together all these sets of numbers make the real number set. However, some problems are not solvable on the set of real numbers. For example, the following equation has no real solution.
x2 + 4 = 0
x2 = −4
$$ x = ±\sqrt{-4} $$
In grade school, students are taught that there are no such things as square roots of negative numbers because squaring a real number always produces a positive number. But what if that was not the case. There are more number sets, called imaginary numbers and complex numbers that will solve this problem.
The picture in figure 1 is part of the Mandelbrot Set which is created using complex numbers.
Finding the square root of a negative number is similar to finding the square root of a positive number. The only change is what to do with the negative sign. Imaginary numbers are square roots of negative numbers. The imaginary unit, i is defined as the square root of −1.
$$ i = \sqrt{-1} $$
Squaring both sides produces,
i2 = −1
The name "imaginary" is somewhat of a bad name. They follow all the rules of "real" numbers. They are not just made up, but come from solving math problems. Don't let the name fool you.
Complex numbers are the combined real set and imaginary set of numbers. They are written with a real and an imaginary part in the form of a + bi such as the number below. The blue part is real and the red part with i is imaginary.
2 + 3i
Real Imaginary
A complex number is a number of the form a + bi where
If b = 0 then a + bi is a real number. If a = 0 and b ≠ 0, the complex number is called an imaginary number.
Evaluate \(\sqrt{-18}\).
Solution
Start by expressing the square as \(\sqrt{a}\sqrt{-1}\).
$$ \sqrt{-18} = \sqrt{18}\sqrt{-1} $$
Replace the \(\sqrt{-1}\) with i.
$$ = \sqrt{18}i $$
Simplify the \(\sqrt{18}\).
$$ = \sqrt{9}\sqrt{2}i $$
$$ = 3\sqrt{2}i $$
Evaluate \(\sqrt{-24}\).
Answer
\(2\sqrt{6}i\)
Real numbers are graphed on a number line; however, complex numbers cannot be graphed on the real number line. To graph complex numbers, a second number line is drawn perpendicular to the real number line. This is the complex plane in which the horizontal axis is the real number line, and the vertical axis is the imaginary number line. Complex numbers in the form a + bi are graphed by plotting the points (a, b) on the complex plane.
In the complex plane, the horizontal axis is the real axis, and the vertical axis is the imaginary axis as shown in figure 2.
For a complex number, a + bi,
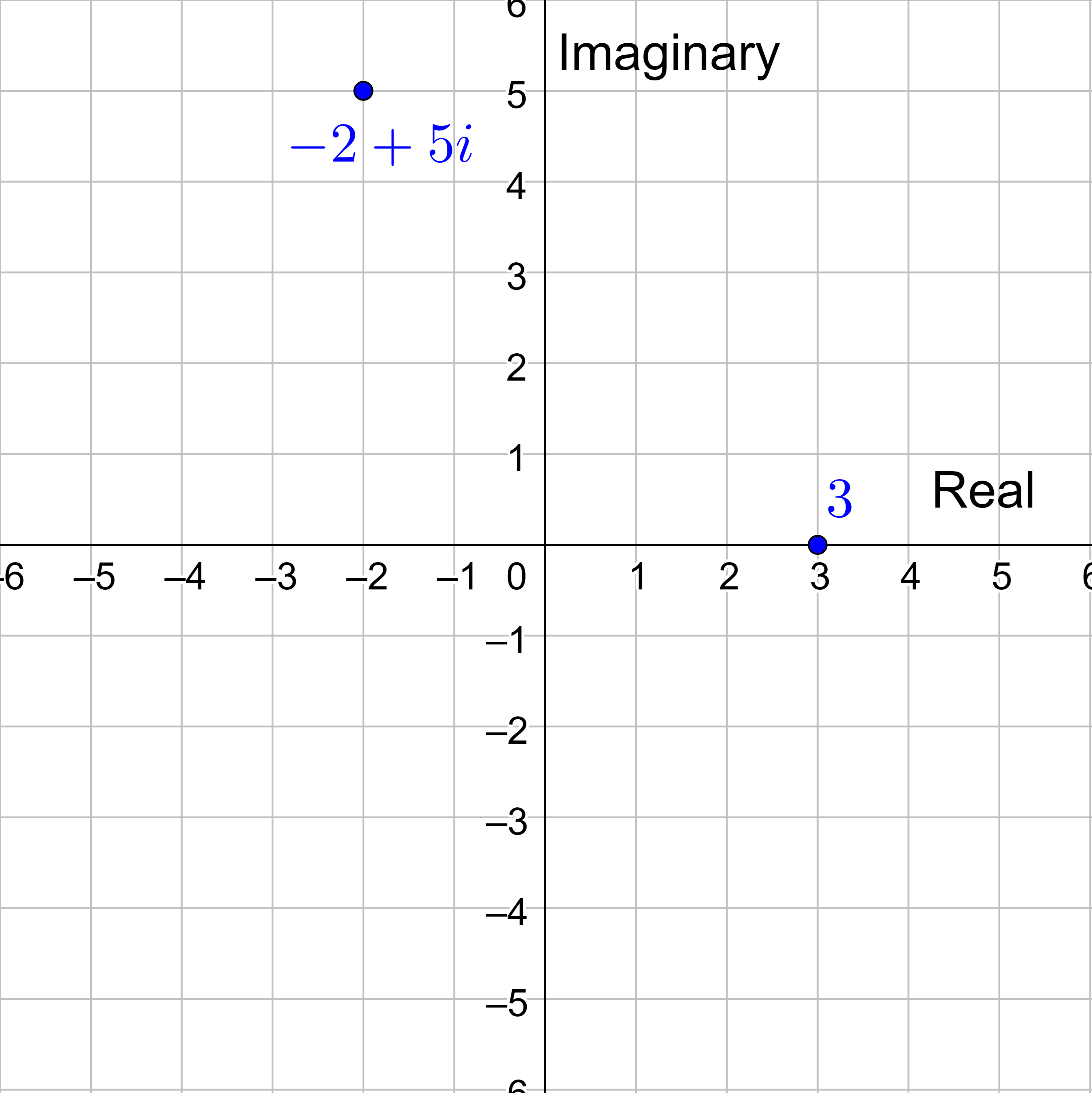
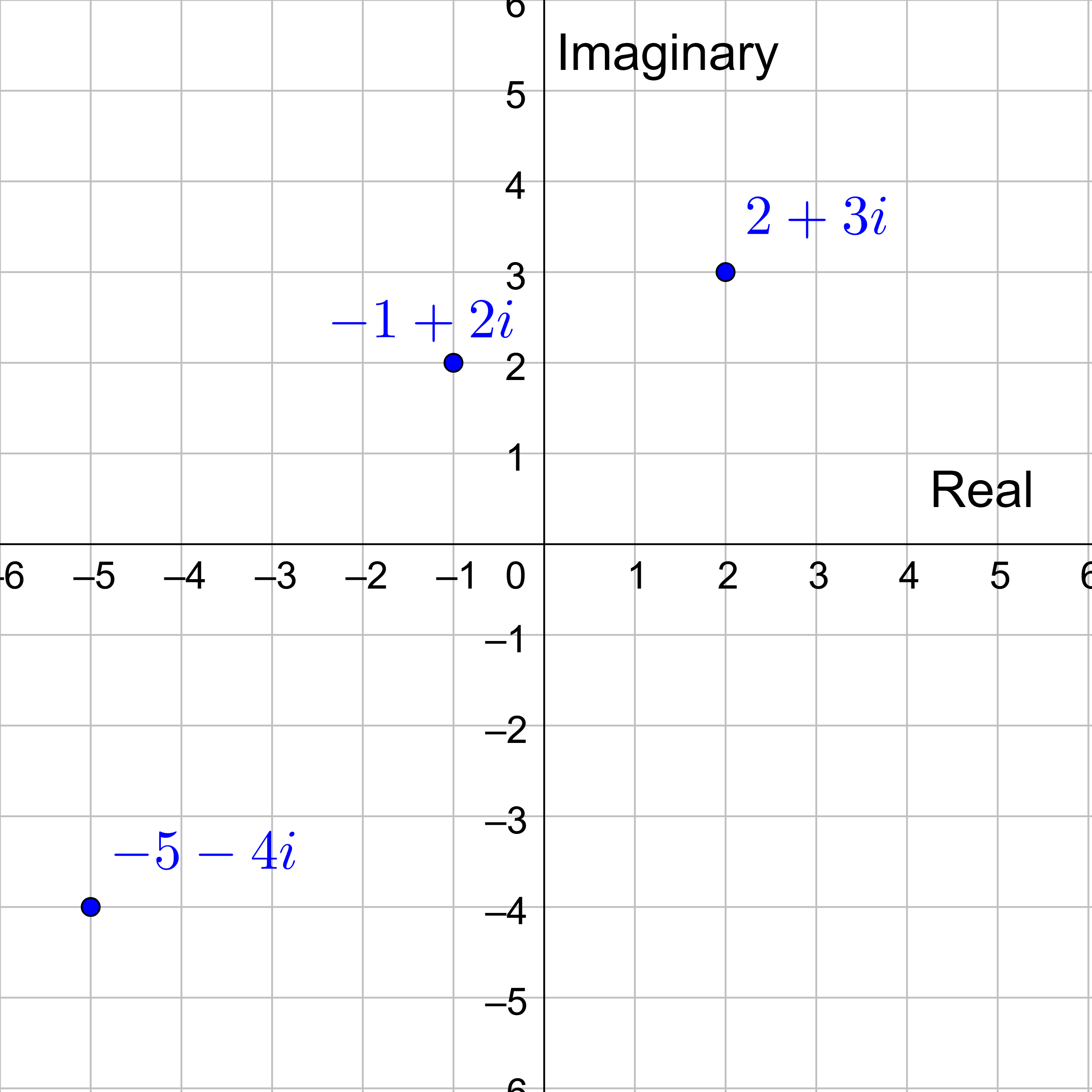
Plot the complex numbers (a) 2 + 3i, (b) −1 + 2i, and (c) −5 − 4i on the complex plane.
Solution
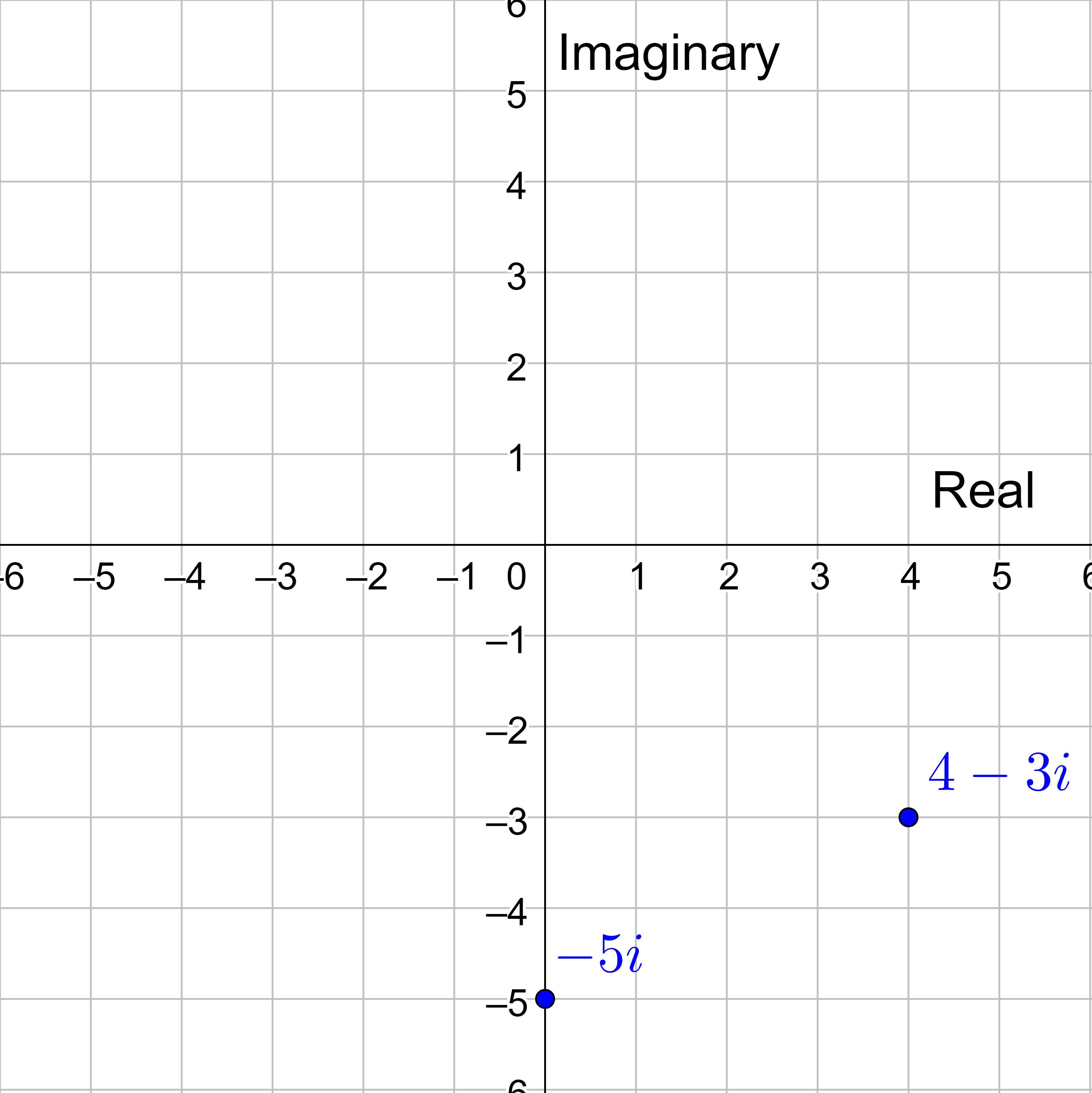
Plot the complex number 3 − 4i on the complex plane.
Answer
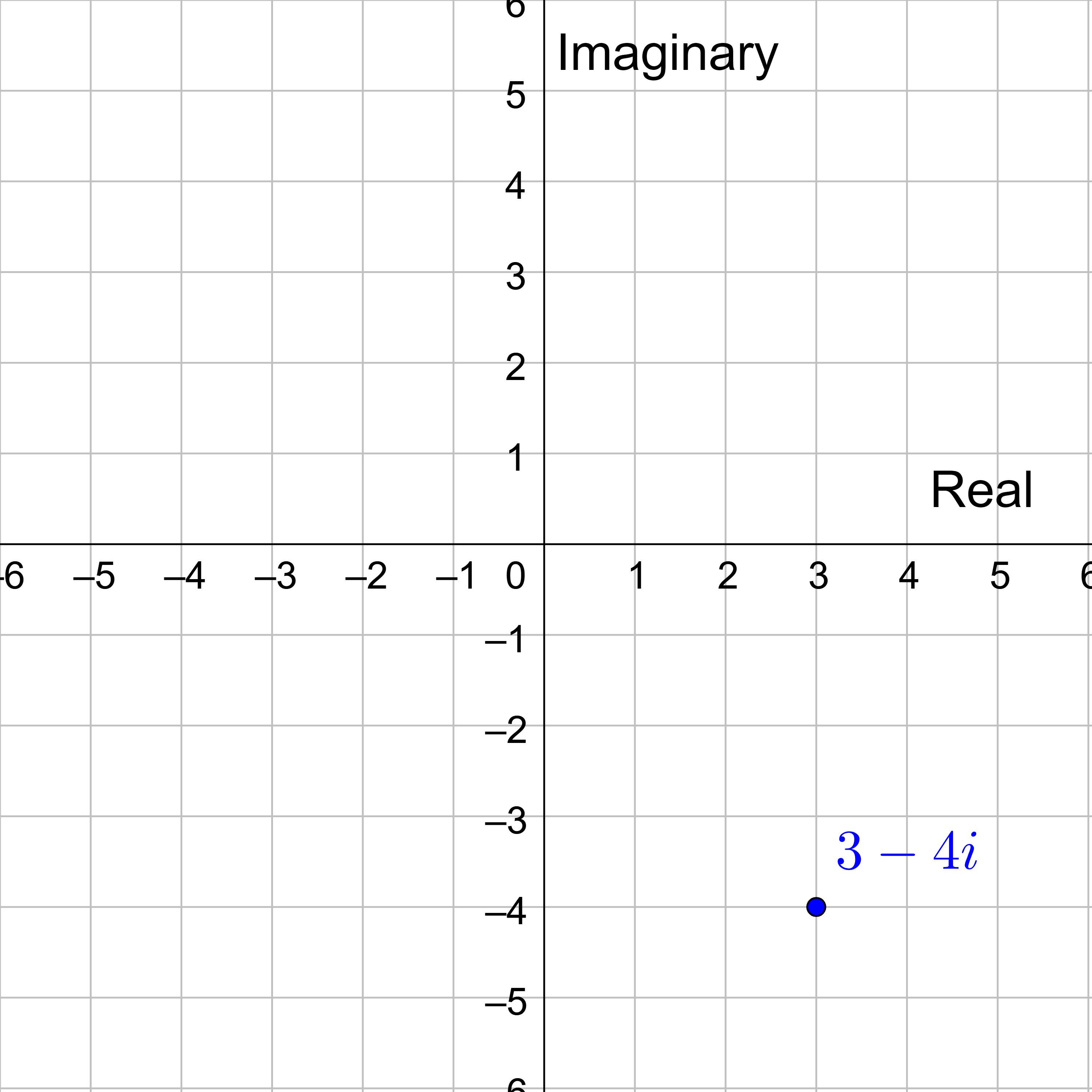
All the normal arithmetic operations work with complex numbers like they do with real numbers. Add or subtract complex numbers by combining the corresponding parts, similar to combining like terms.
Adding complex numbers:
(a + bi) + (c + di) = (a + c) + (b + d)i
Subtracting complex numbers:
(a + bi) − (c + di) = (a − c) + (b + d)i
Essentially, this is combining like terms.
Simplify (2 + 3i) + (−3 + 5i).
Solution
Combine like terms. Add the real parts, then add the imaginary parts.
(2 + 3i) + (−3 + 5i)
(2 + (−3)) + (3i + 5i)
−1 + 8i
Simplify (2 + 4i) − (−3 + 5i).
Answer
5 − i
Multiplying complex numbers is similar to multiplying binomials. The major difference is to replace any i2 to −1. Use the distributive property to multiply each term in the first complex number with each term in the second complex number. If i2 results, change it to −1. Then collect like terms.
(a + bi)(c + di)
ac + adi + bci + bdi2
ac + adi + bci − bd
(ac − bd) + (ad + bc)i
Simplify 3(5 + 2i).
Solution
Distribute the 3.
3(5 + 2i)
= (3·5) + (3·2)i
= 15 + 6i
Simplify −2(1 + 5i).
Answer
−2 − 10i
Simplify (2 + 3i)(1 − 4i).
Solution
Use the distributive property.
(2 + 3i)(1 − 4i)
= (2·1) + (2·−4i) + (3i·1) + (3i·−4i)
= 2 − 8i + 3i − 12i2
Replace the i2 with −1.
= 2 − 8i + 3i − 12(−1)
= 2 − 8i + 3i + 12
Collect like terms.
= 14 − 5i
Simplify (3 − i)(5 + 2i).
Answer
17 + i
Division of two complex numbers is more complicated than addition, subtraction, and multiplication because the imaginary unit, i, is technically a radical, and no radicals are allowed in the denominator of a number. However, division by complex numbers is the same as division by radicals. To divide complex numbers, multiply the numerator and denominator by the complex conjugate of the denominator. The complex conjugate is the same number, but with the opposite sign on the imaginary part. The complex conjugate of a + bi is a − bi.
To divide a + bi by c + di where neither c nor d equals zero, first write the division as a fraction. Then find the complex conjugate of the denominator, and multiply both the numerator and the denominator.
$$ \frac{a+bi}{c+di} $$
Multiply the numerator and denominator by the complex conjugate of the denominator.
$$ \frac{a+bi}{c+di}·\frac{c-di}{c-di} $$
Apply the distributive property.
$$ \frac{ac - adi + bci - bdi^2}{c^2 - cdi + cdi - d^2i^2} $$
Simplify, remembering that i2 = −1.
$$ \frac{ac - adi + bci - bd(-1)}{c^2 - cdi + cdi - d^2(-1)} $$
$$ \frac{(ac + bd) + (bc - ad)i}{c^2 + d^2} $$
The complex conjugate of a complex number a + bi is a − bi. It is the same number with the opposite sign on the imaginary part.
Find the complex conjugate of each number.
Solution
Divide (1 − 4i) by (3 + i).
Solution
Write the problem as a fraction.
$$ \frac{1 - 4i}{3 + i} $$
Multiply the numerator and denominator by the complex conjugate of the denominator.
$$ \frac{1 - 4i}{3 + i}⋅\frac{3 - i}{3 - i} $$
Multiply the complex numbers using the distributive property.
$$ \frac{(1 - 4i)(3 - i)}{(3 + i)(3 - i)} $$
$$ \frac{1 - i - 12i + 4i^2}{9 - 3i + 3i - i^2} $$
Replace i2 with −1 and simplify.
$$ \frac{1 - i - 12i + 4(-1)}{9 - 3i + 3i - (-1)} $$
$$ \frac{-3 - 13i}{10} $$
Separate into real and imaginary parts.
$$ -\frac{3}{10} - \frac{13}{10}i $$
Simplify \(\frac{2 - i}{3i}\).
Answer
\(-\frac{1}{3} - \frac{2}{3}i\)
Let f(x) = x2 + 3x. Evaluate f(2 − i).
Solution
Substitute x = 2 − i into the function f(x) = x2 + 3x and simplify.
f(2 − i) = (2 − i)2 + 3(2 − i)
Use the distributive property. Remember that (2 − i)2 = (2 − i)(2 − i).
= 4 − 4i + i2 + 6 − 3i
Replace i2 with −1.
= 4 − 4i + (−1) + 6 − 3i
Collect like terms.
= 9 − 7i
Let f(x) = 2x2 − x. Evaluate f(3 − 2i).
Answer
2 − 10i
Let \(f(x) = \frac{x}{x + 1}\). Evaluate f(2 + i).
Solution
$$ f(x) = \frac{x}{x + 1} $$
Substitute x = 2 + i.
$$ f(2 + i) = \frac{2 + i}{(2 + i) + 1} $$
$$ = \frac{2 + i}{3 + i} $$
Because this is division, multiply the numerator and denominator by the conjugate of the denominator.
$$ = \frac{(2 + i)}{(3 + i)}⋅\frac{(3 - i)}{(3 - i)} $$
Use the distributive property.
$$ = \frac{6 - 2i + 3i - i^2}{9 - 3i + 3i - i^2} $$
Replace i2 with −1.
$$ = \frac{6 - 2i + 3i - (-1)}{9 - 3i + 3i - (-1)} $$
Combine like terms.
$$ = \frac{7 + i}{10} $$
Put the number in standard form by splitting it into real and imaginary parts.
$$ = \frac{7}{10} + \frac{1}{10}i $$
Let \(f(x) = \frac{1 - x}{x + 2}\). Evaluate 1 − 4i.
Answer
\(-\frac{16}{25} + \frac{12}{25}i\)
The powers of i follow a pattern. The items in the list below are increasing powers of i. What is the pattern?
i1 = i
i2 = −1
i3 = i2·i = (-1)·i = −i
i4 = i3·i = −i·i = −i2 = −(−1) = 1
i5 = i4·i = 1·i = i
i6 = i5·i = i·i = i2 = −1
i7 = i6·i = (−1)·i = −i
i8 = i7·i = −i·i = −i2 = −(−1) = 1
i9 = i8·i = 1·i = i
The powers of i follow a four-part cycle. To find the value of a power of i, divide the exponent by 4 and find the remainder. The value of the power of i is the same as the value of iremainder.
To evaluate a power of i,
Evaluate i51.
Solution
Divide 51 by 4 and find the remainder.
$$ \frac{51}{4} = 12 R 3 $$
Since the remainder is 3, i51 = i3 = −i.
A complex number is a number of the form a + bi where
In the complex plane, the horizontal axis is the real axis, and the vertical axis is the imaginary axis as shown in figure 2.
For a complex number, a + bi,
Adding complex numbers:
(a + bi) + (c + di) = (a + c) + (b + d)i
Subtracting complex numbers:
(a + bi) − (c + di) = (a − c) + (b + d)i
Essentially, this is combining like terms.
The complex conjugate of a complex number a + bi is a − bi. It is the same number with the opposite sign on the imaginary part.
To evaluate a power of i,
Helpful videos about this lesson.
| 1 | 2 | 3 | 4 | 5 |
| 10 | 8 | 6 | 4 | 2 |
