Precalculus by Richard Wright
Precalculus by Richard Wright
Blessed are the meek, for they will inherit the earth. Matthew 5:5 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.4.1, PC.5.3

The water in a fountain follows a curved path. The water is launched from the fountain. Then only gravity influences the water's motion until it hits the pool on the other side. This is called projectile motion and can be modeled by a quadratic function.
A quadratic function is a simple polynomial function where the highest exponent on x is 2. They can be written as f(x) = ax2 + bx + c. The graph of a quadratic function is called a parabola.
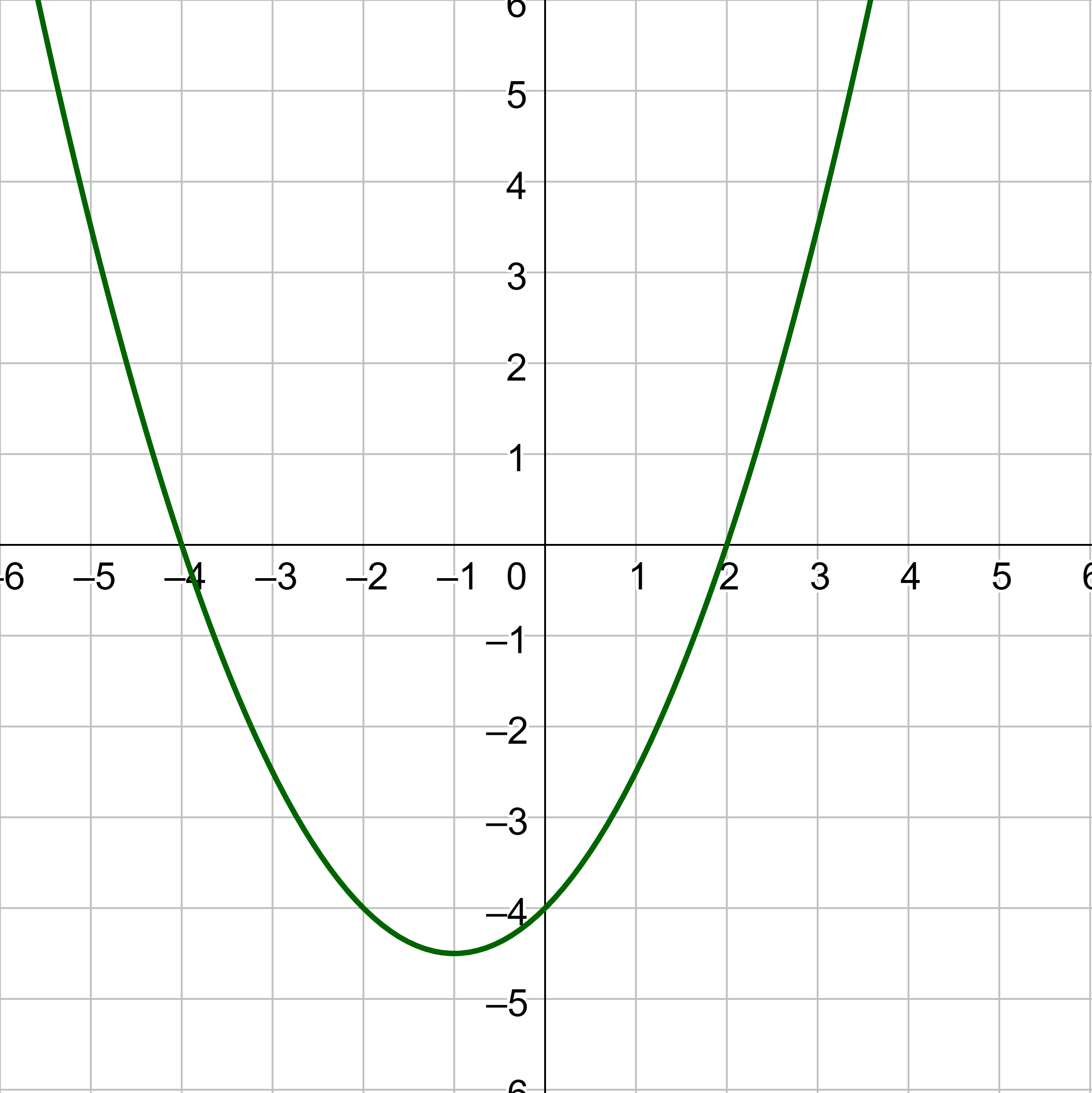
The graph of a quadratic function is a U-shaped curve called a parabola. An important feature of a parabola is its extreme point, called the vertex. If the parabola opens up, the vertex represents the lowest point on the graph, or the minimum value of the quadratic function. If the parabola opens down, the vertex represents the highest point on the graph, or the maximum value. In either case, the vertex is a turning point on the graph. The graph is also symmetric with a vertical line drawn through the vertex, called the axis of symmetry. See figure 2.
The y-intercept is the point at which the parabola crosses the y-axis. The x-intercepts are the points at which the parabola crosses the x-axis. If they exist, the x-intercepts represent the zeros, or roots, of the quadratic function, which are the values of x when y = 0.
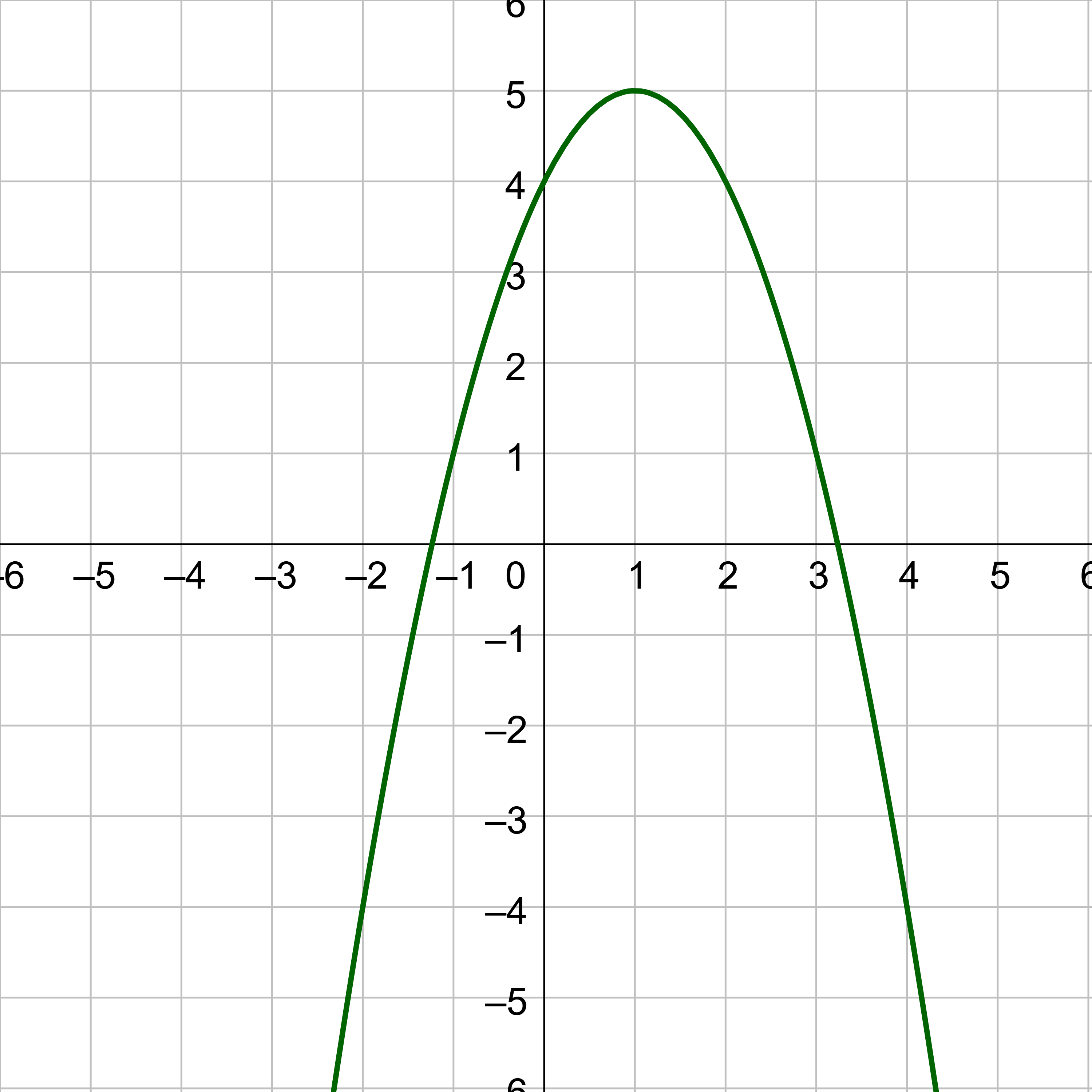
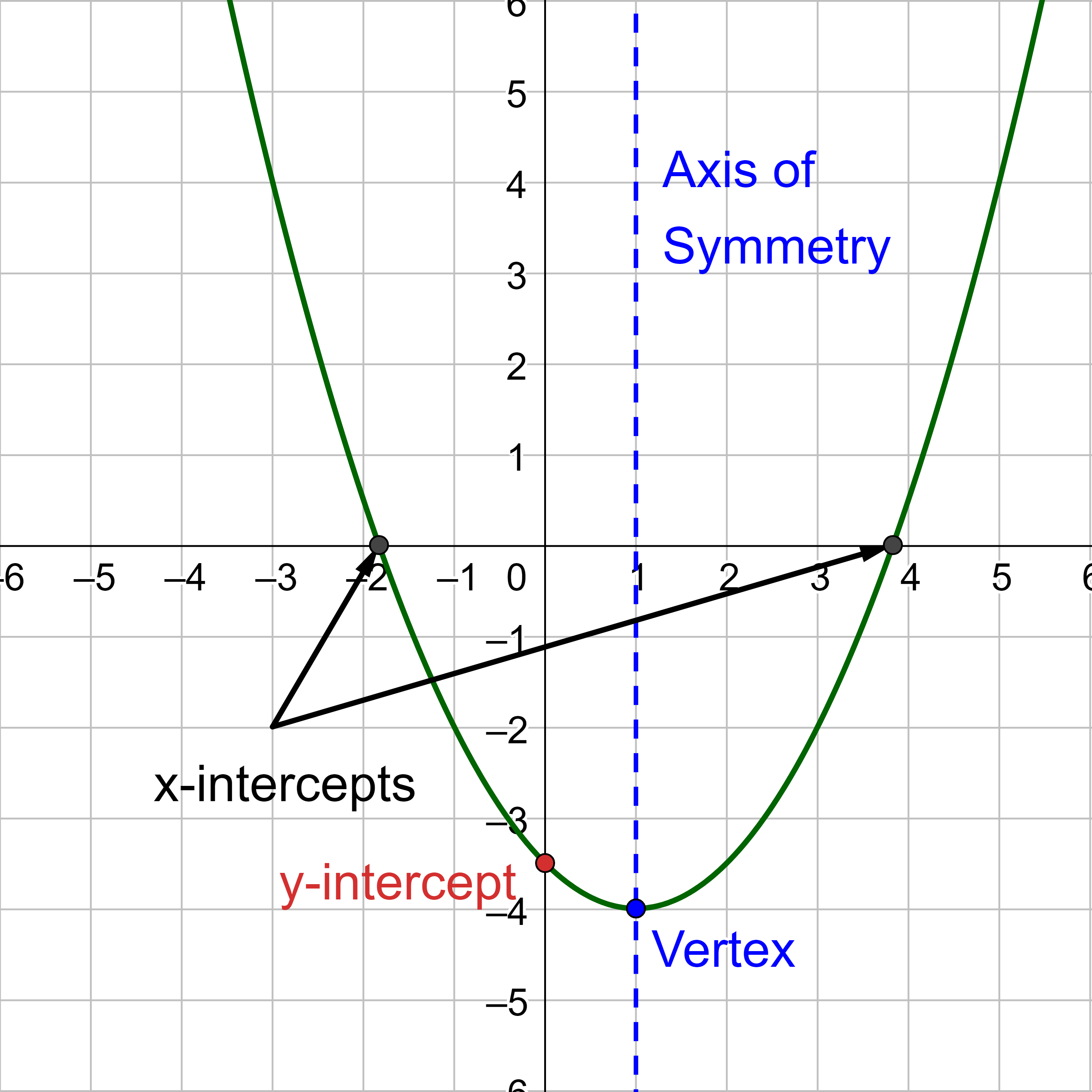
Determine the vertex, axis of symmetry, zeros, and y-intercept of the parabola shown in figure 3.
Solution
The vertex is the turning point and lowest point on the graph. That appears to be (−2, 0).
The axis of symmetry is the vertical line through the vertex and is x = −2.
The zeros are the x-intercepts where the graph intersects the x-axis. That appears to be (−2, 0).
The y-intercept is where the graph intersects the y-axis. That is (0, 4).
The general form of a quadratic function is
f(x) = ax2 + bx + c
where a, b, and c are real numbers and a ≠ 0. If a > 0, the parabola opens upward. If a < 0, the parabola opens downward.
The axis of symmetry is found by
$$ x = \frac{-b}{2a} $$
Compare that to the quadratic formula.
$$ x = \frac{-b±\sqrt{b^2 - 4ac}}{2a} $$
$$ = \frac{-b}{2a} ± \frac{\sqrt{b^2 - ac}}{2a} $$
Notice that the first part of the quadratic formula is the axis of symmetry. The second part is the distance the x-intercepts are away from the axis of symmetry.
The y-intercept is easy to find from the general form. Let x = 0 and simplify.
y = ax2 + bx + c
y = a(0)2 + b(0) + c
y = c
The y-intercept is (0, c).
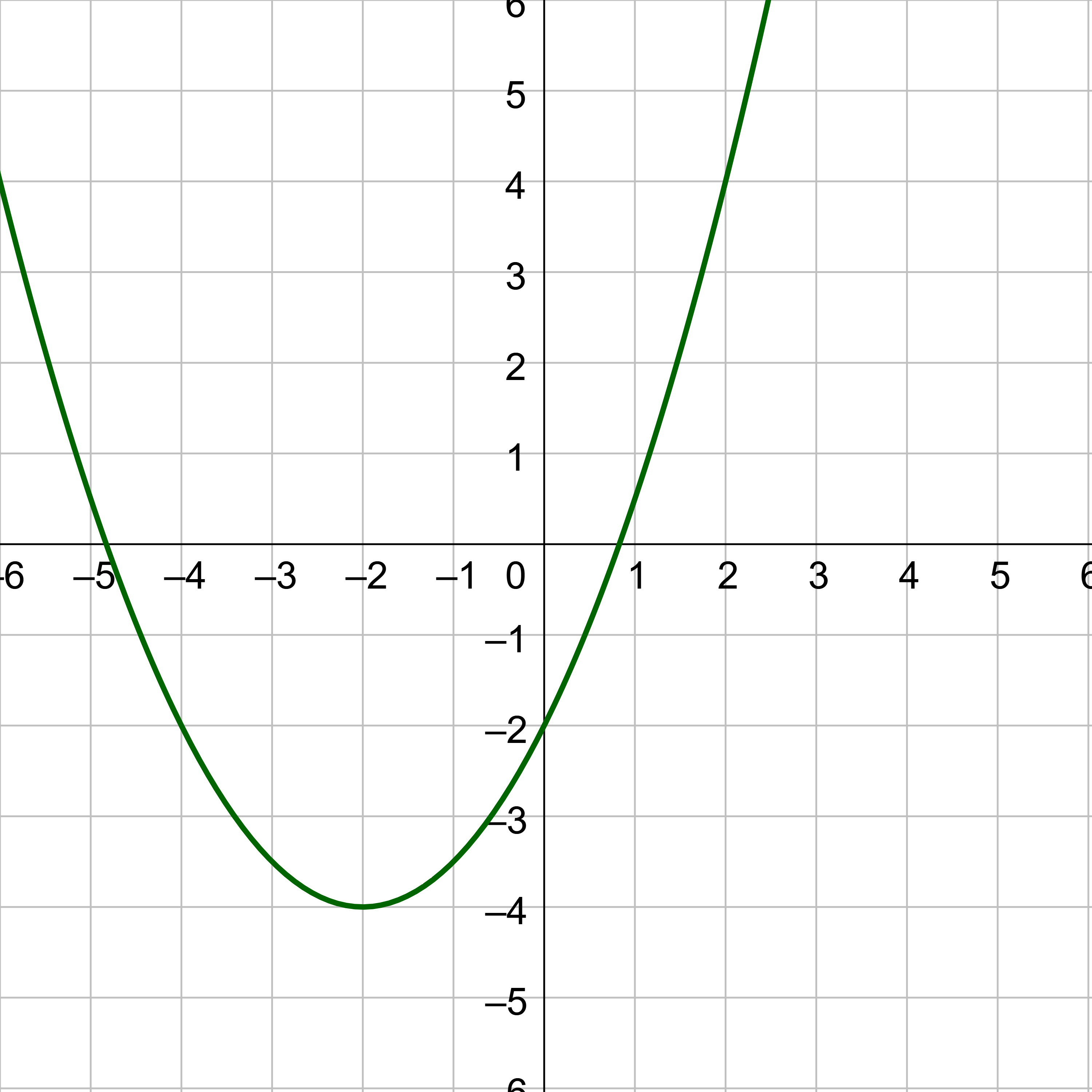
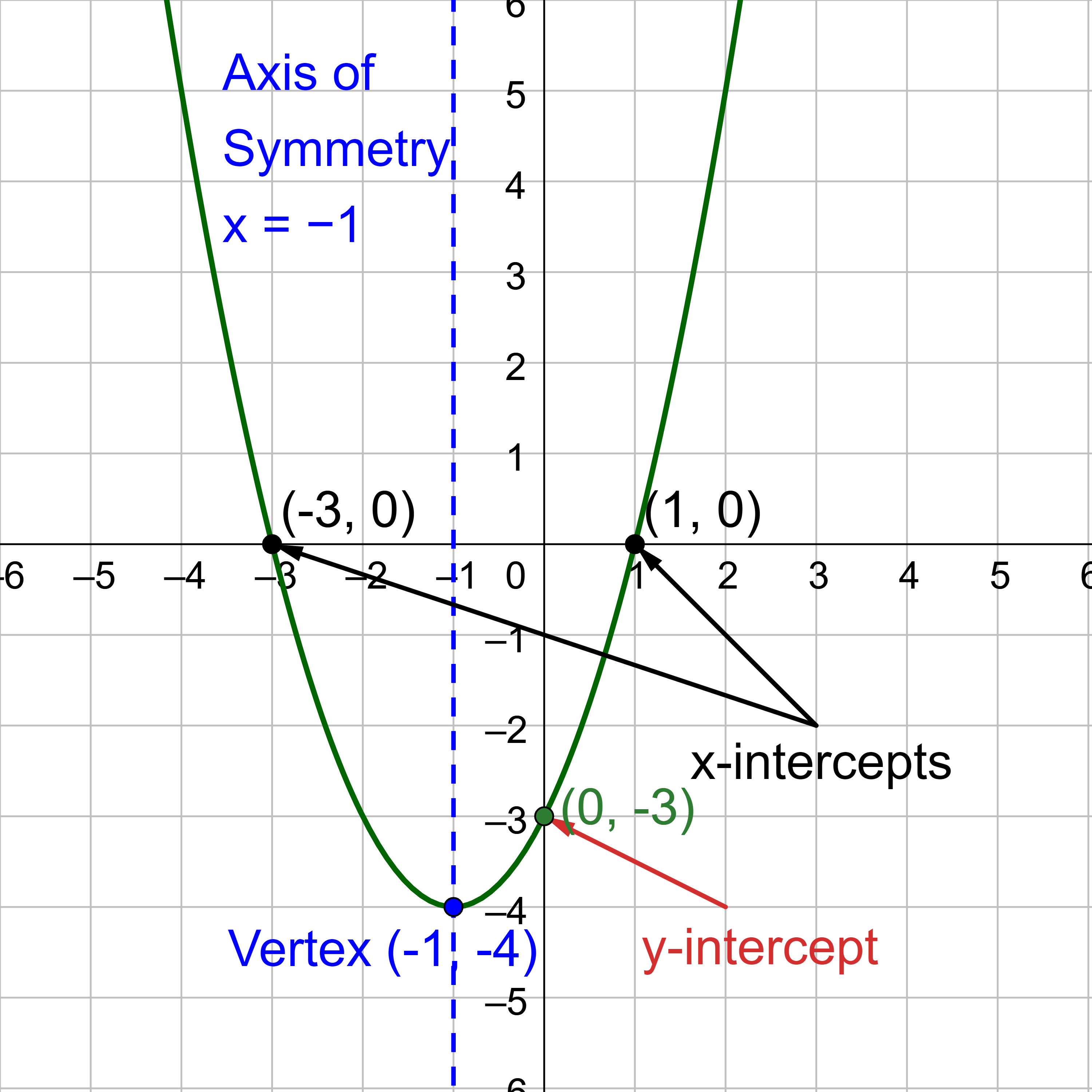
Figure 4 represents the graph of the quadratic function y = x2 + 2x − 3. In this form, a = 1, b = 2, and c = −3. Because a > 0, the parabola opens upward. The axis of symmetry is \(x = \frac{-b}{2a} = \frac{-2}{2⋅1} = -1\). This makes sense because the vertical line x = −1 divides the graph in half. The vertex always occurs along the axis of symmetry. For a parabola that opens upward, the vertex occurs at the lowest point on the graph, in this instance, (−1, −4). The x-intercepts, which are those points where the parabola crosses the x-axis, occur at (−3, 0) and (1, 0).
f(x) = ax2 + bx + c
The standard form of a quadratic function is
f(x) = a(x − h)2 + k
where (h, k) is the vertex. Because the vertex appears in the standard form of the quadratic function, this form is also known as the vertex form of a quadratic function.
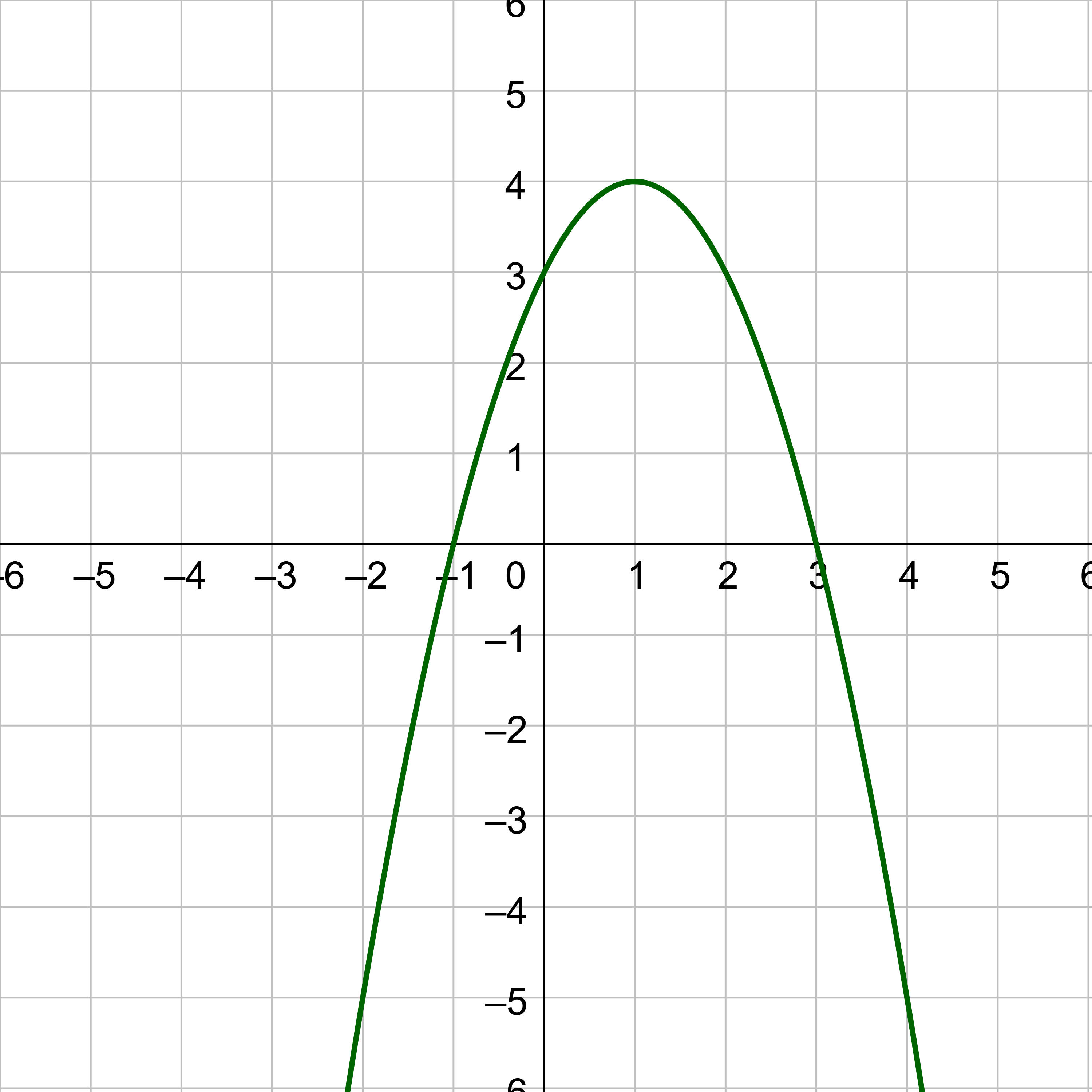
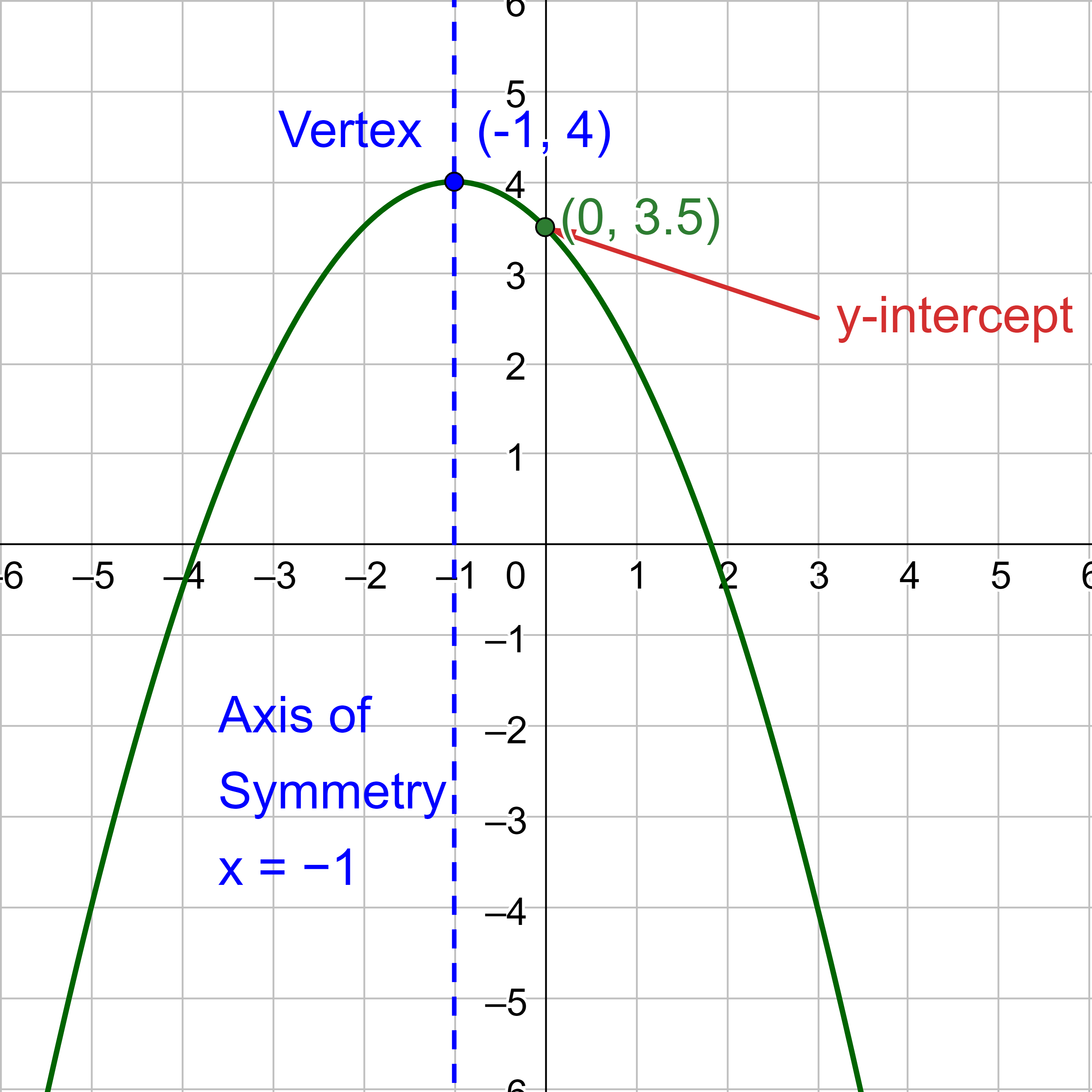
Like in the general form, if a > 0, the parabola opens upward, and the vertex is a minimum. If a < 0, the parabola opens downward, and the vertex is a maximum. Figure 5 is the graph of the quadratic function \(y = -\frac{1}{2}(x + 1)^2 + 4\). Since x − h = x + 1 in this example, h = −1. In this example, \(a = -\frac{1}{2}\), h = −1, and k = 4. Because a < 0, the parabola opens downward. The vertex is at (−1, 4).
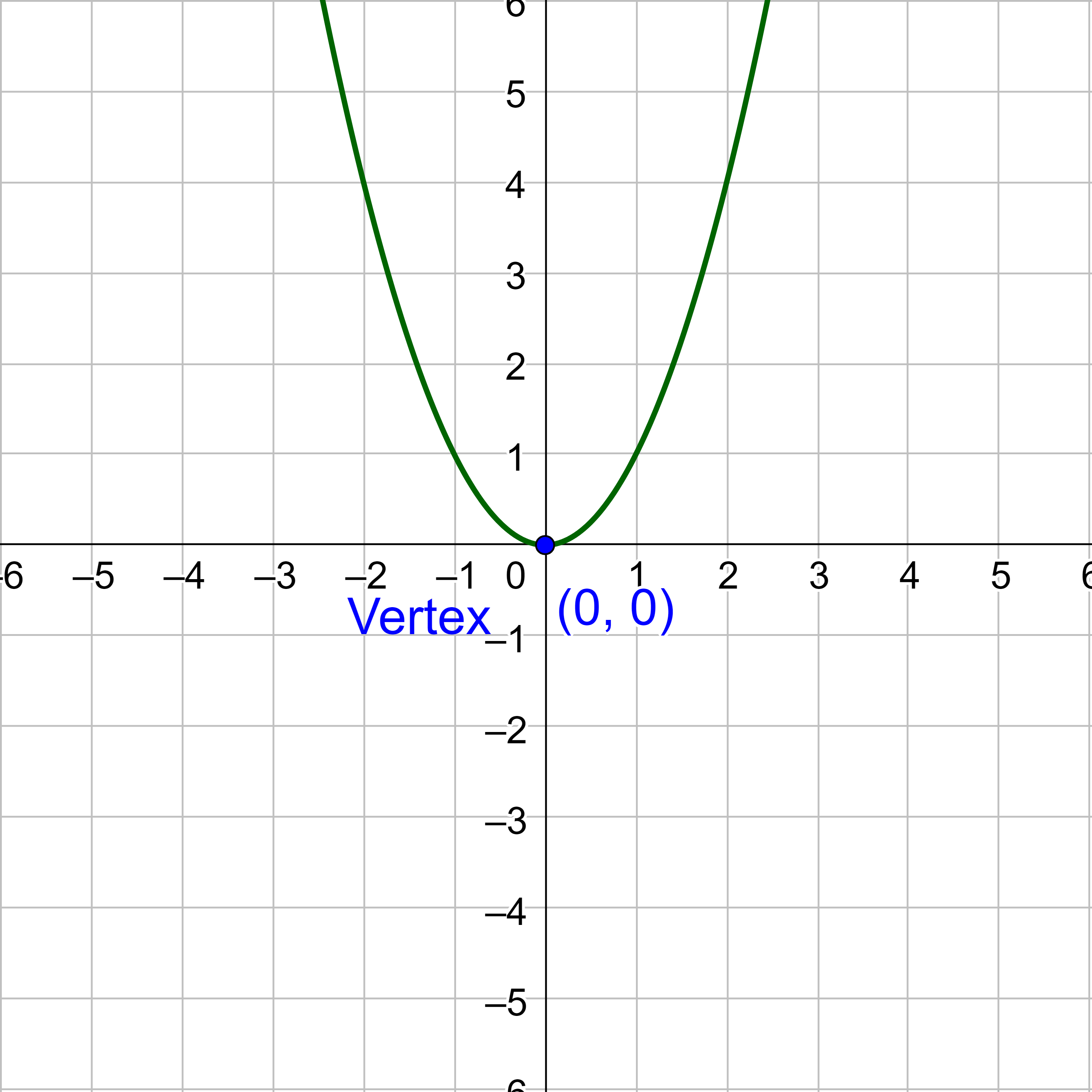
The standard form is useful for determining the transformations from the graph of y = x2. Figure 6 is the graph of this basic function.
If k > 0, the graph shifts upward, but if k < 0, the graph shifts downward. In figure 5, k > 0, so the graph is shifted 4 units upward. If h > 0, the graph shifts toward the right and if h < 0, the graph shifts to the left. In figure 5, h < 0, so the graph is shifted 1 unit to the left. The magnitude of a indicates the stretch of the graph. If |a| > 1, the graph is stretched vertically, but the point associated with a particular x-value shifts farther from the x-axis, so the graph appears to become narrower. But if |a| < 1, the graph is shrunk vertically, and the point associated with a particular x-value shifts closer to the x-axis, so the graph appears to become wider. In figure 5, |a| < 1, so the graph is shrunk vertically and looks wider.
The standard form and the general form are equivalent methods of describing the same function. Explore this by expanding out the general form and setting it equal to the standard form.
a(x − h)2 + k = ax2 + bx + c
a(x2 − 2hx + h2) + k = ax2 + bx + c
ax2 − 2ahx + (ah2 + k) = ax2 + bx + c
For the corresponding terms to be equal, the coefficients must be equal. Notice both sets have ax2, so the a's meaning is identical for both forms. Set the middle term's coefficients equal to see how those variables correspond.
−2ah = b
$$ h = \frac{-b}{2a} $$
This is the axis of symmetry. In standard form, the axis of symmetry is x = h which is the same as \(x = \frac{-b}{2a}\) in general form. These are also the x-coordinates of the vertex since it is always on the axis of symmetry.
Set the constant terms equal.
ah2 + k = c
Thus, the y-intercept is (0, ah2 + k) in vertex form, or (0, c) in general form.
Sometimes called the vertex form.
f(x) = a(x − h)2 + k
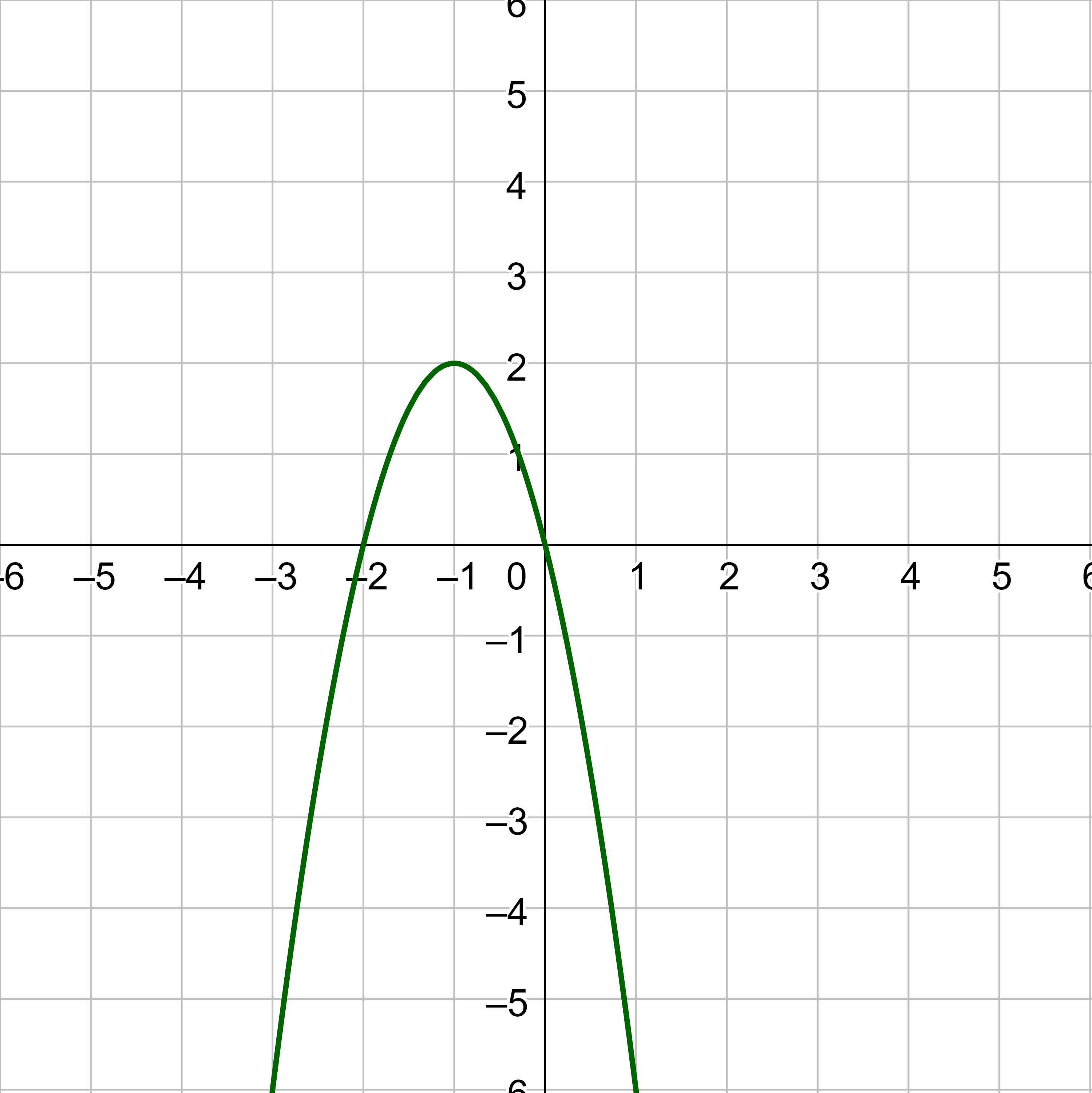
Write an equation for the quadratic function in figure 7 and simplify to write the equation in general form.
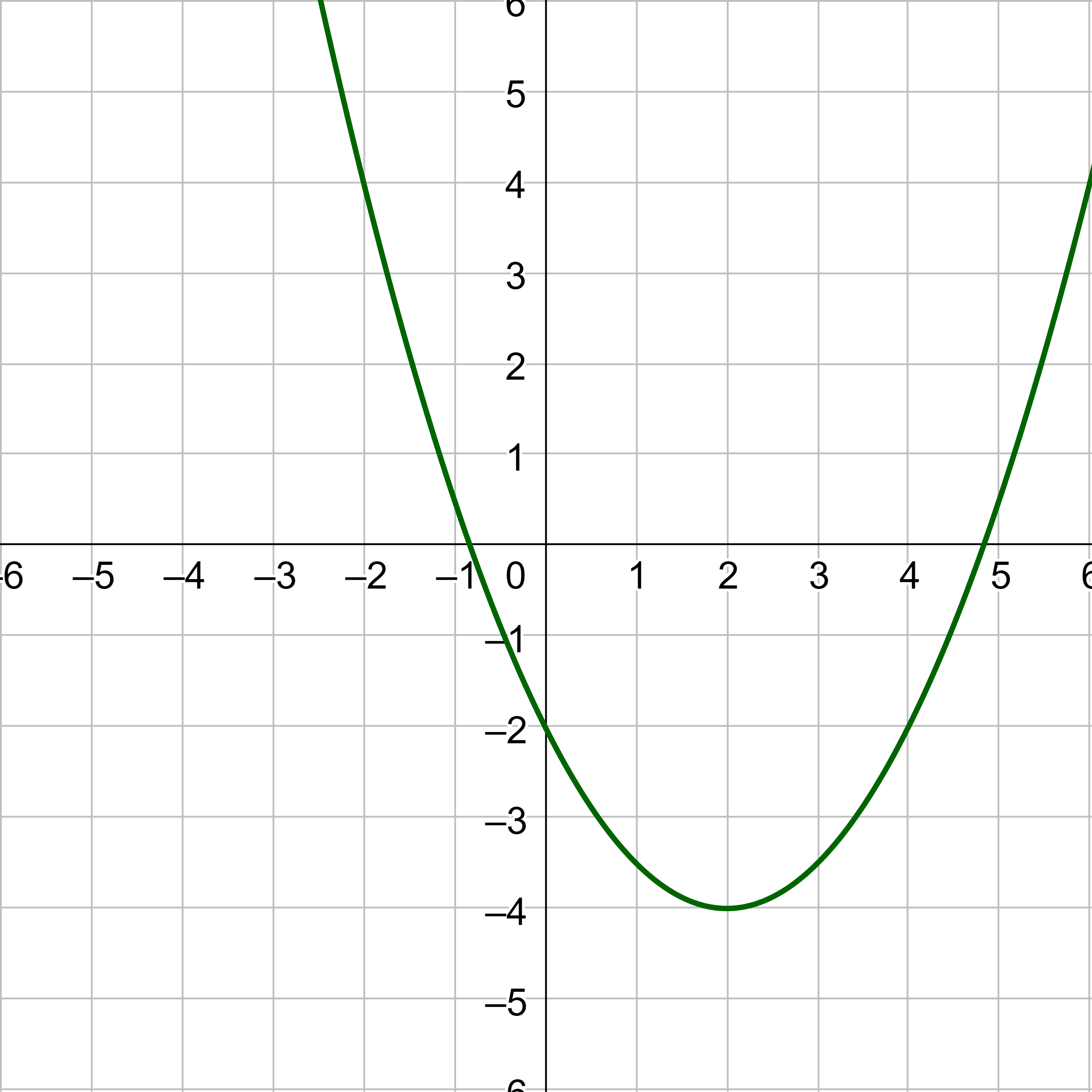
Solution
The vertex is (2, −4), so h = 2 and k = −4. Substitute those into the standard form.
f(x) = a(x − h)2 + k
f(x) = a(x − 2)2 − 4
Choose some point on the parabola such as (0, −2). Substitute those for x and f(x).
−2 = a(0 − 2)2 − 4
Solve for a.
−2 = 4a − 4
2 = 4a
$$ \frac{1}{2} = a $$
Substitute \(a = \frac{1}{2}\), h = 2, and k = −4 into standard form.
$$ f(x) = \frac{1}{2}(x - 2)^2 - 4 $$
Expand and simplify.
$$ f(x) = \frac{1}{2}(x^2 - 4x + 4) - 4 $$
$$ f(x) = \frac{1}{2}x^2 - 2x + 2 - 4 $$
$$ f(x) = \frac{1}{2}x^2 - 2x - 2 $$
Write an equation for the quadratic function in figure 8 and simplify to write the equation in general form.
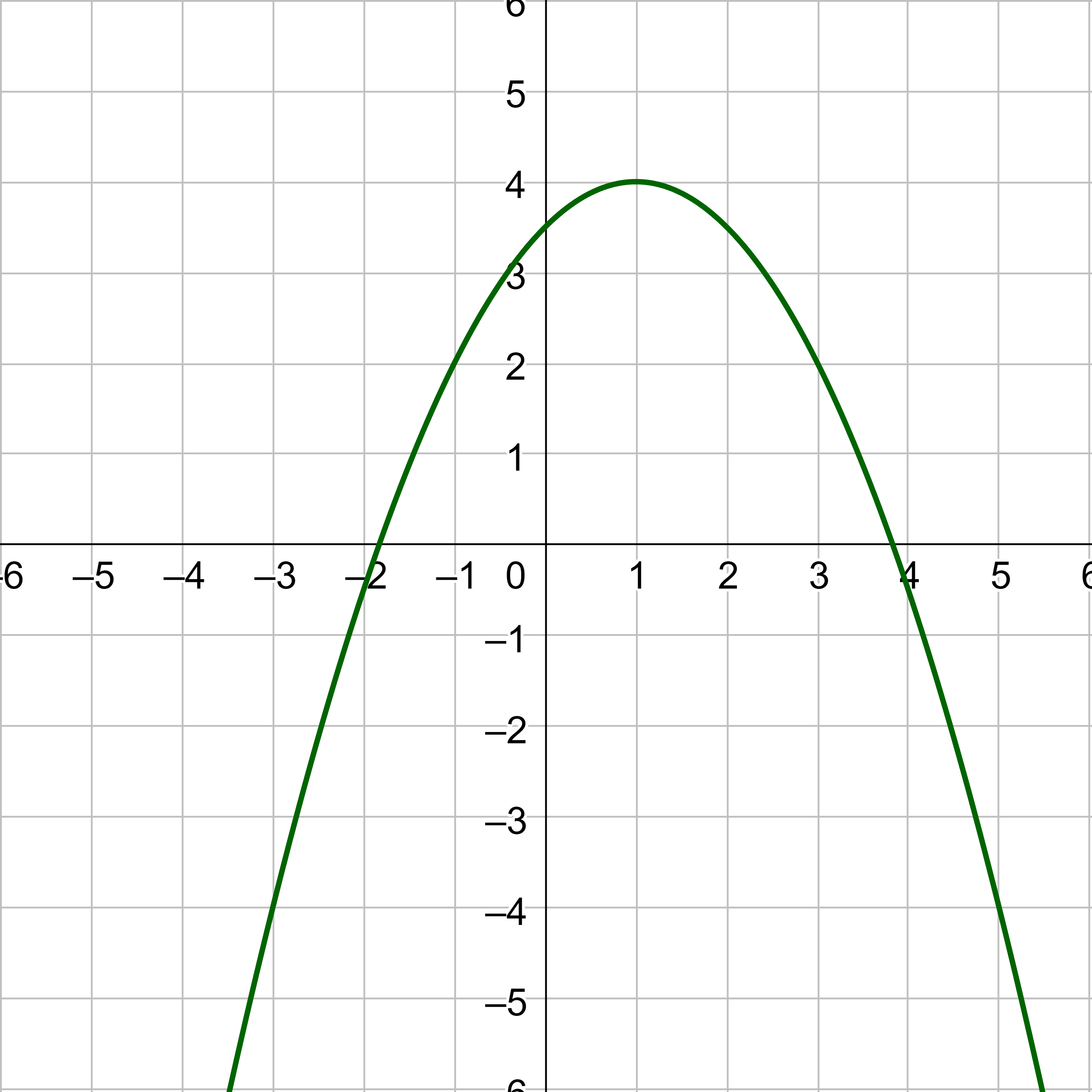
Answer
\(f(x) = -\frac{1}{2}x^2 + x + \frac{7}{2}\)
Find the vertex of the quadratic function f(x) = 2x2 + 2x − 24. Rewrite the quadratic in standard form.
Solution
This is in general form, ax2 + bx + c, so a = 2, b = 2, and c = −24. The x-coordinate of the vertex is at
$$ x = \frac{-b}{2a} $$
$$ x = \frac{-2}{2⋅2} $$
$$ x = -\frac{1}{2} $$
The y-coordinate of the vertex is found by substituting the x-coordinate of the vertex into the function.
f(x) = 2x2 + 2x − 24
$$ f\left(-\frac{1}{2}\right) = 2\left(-\frac{1}{2}\right)^2 + 2\left(-\frac{1}{2}\right) - 24 $$
$$ f\left(-\frac{1}{2}\right) = \frac{1}{2} - 1 - 24 $$
$$ f\left(-\frac{1}{2}\right) = -\frac{51}{2} $$
The vertex is \(\left(-\frac{1}{2}, -\frac{51}{2}\right)\)
Write the equation in standard form by substituting the vertex (h, k) and a into standard form.
f(x) = a(x − h)2 + k
$$ f(x) = 2\left(x + \frac{1}{2}\right)^2 - \frac{51}{2} $$
Find the vertex and then write the equation in standard form. g(x) = x2 + 2x − 8
Answer
(−1, −9); g(x) = (x + 1)2 − 9
Many application problems about quadratic functions want the maximum or minimum. These include problems such as, "How high will the ball go?", "What is the maximum revenue?", or "What is the minimum cost?" Because the vertex is the highest or lowest point, the maximum or minimum value is the y-coordinate, or output, of the vertex.
A backyard farmer wants to enclose a rectangular space for a chicken run within her fenced backyard. She has purchased 80 feet of wire fencing to enclose three sides, and she will use a section of the backyard fence as the fourth side.
Solution
Use a diagram to visualize the given information. It is also helpful to introduce a temporary variable, W, to represent the width of the chicken run and the length of the fence section parallel to the backyard fence.
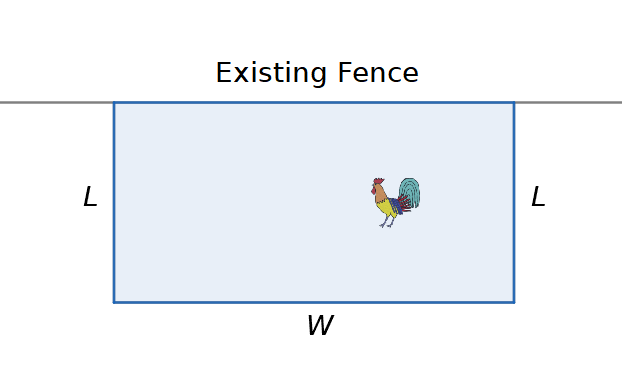
Area of a rectangle is A = LW. Find an expression for the width by using the part of the perimeter that will be created with the new fence.
P = 2L + W
W = P – 2L
W = 80 – 2L
Substitute this into the area equation.
A = LW
A = L(80 – 2L)
Distribute to put into general form.
A = –2L2 + 80L
This is a quadratic function, and the maximum will occur at the vertex. Find the L-coordinate (x-coordinate except this function uses L instead of x).
$$ x = \frac{-b}{2a} $$
$$ L = \frac{-80}{2(-2)} = 20 $$
Substitute this into the function to find the area output of the vertex.
A = –2L2 + 80L
A = –2(20)2 + 80(20)
A = 800
The maximum area is 800 ft2 and occurs when the sides are 20 ft by 40 ft.
The unit price of an item affects its supply and demand. That is, if the unit price goes up, the demand for the item will usually decrease. For example, a local deli currently sells 250 sandwiches during lunch hour at $6 each. When the owner decreased the price by $1, he sold 25 more sandwiches. Assuming that sales are linearly related to the price, what price should the deli charge for a sandwich to maximize their revenue?
Solution
Revenue is the amount of money a company brings in. In simple cases like this, the revenue is the product of the price and the sales, R = p⋅s.
If x stands for the number of times the price decreases by $1, then the price is (6 – 1x). Also, the sales would be (250 + 25x). Thus, the revenue is
R = p⋅s
R = (6 – x)(250 + 25x)
R = 1500 – 150x – 25x2
R = –25x2 – 150x + 1500
This is a quadratic equation that opens down because a is negative. The maximum will occur at the vertex. The x-coordinate of the vertex is
$$ x = \frac{-b}{2a} $$
$$ x = \frac{150}{2(-25)} = -3 $$
This means the price of the sandwiches should decrease –3 times $1, or the price should rise $3. The maximum revenue is found by substituting the x-coordinate of the vertex into the function.
R = –25(–3)2 – 150(–3) + 1500 = 2025
The maximum revenue is $2025 when the price is raised $3 so that the deli charges $9 a sandwich. This will of course result in selling 75 fewer sandwiches.
Any number can be the input value of a quadratic function. Therefore, the domain of any quadratic function is all real numbers. Because parabolas have a maximum or a minimum point, the range is restricted. Since the vertex of a parabola will be either a maximum or a minimum, the range will be all y-values greater than or equal to the y-coordinate at the vertex if it opens up, or less than or equal to the y-coordinate at the vertex if the parabola opens down.
The domain of any quadratic function is all real numbers or (−∞, ∞).
The range of a quadratic function is
where k is the y-coordinate of the vertex.
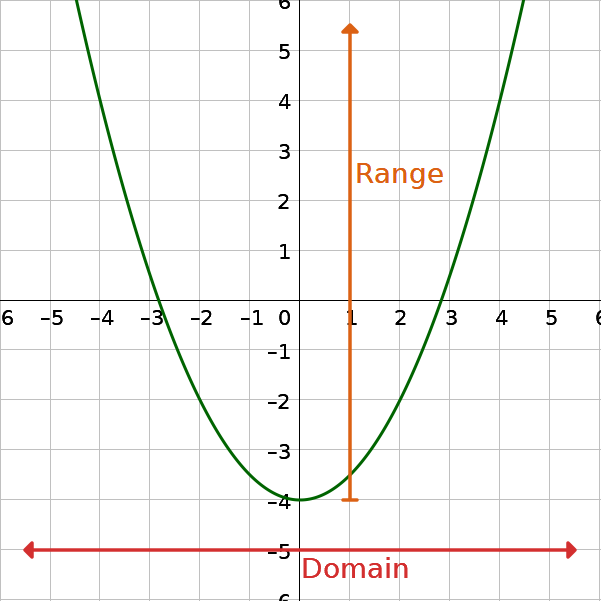
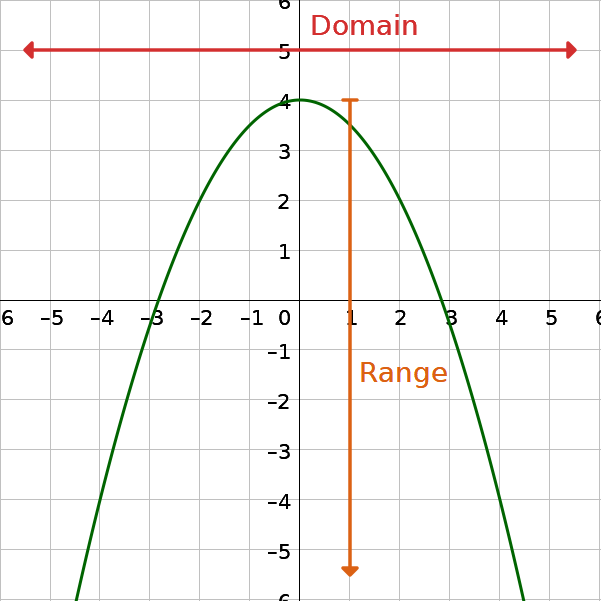
Find the domain and range of f(x) = −2x2 − 7x − 4.
Solution
For all quadratic function, the domain is all real numbers or (−∞, ∞).
To find the range, start by finding the vertex. The x-coordinate of the vertex is \(x = \frac{-b}{2a}\).
$$ x = \frac{-b}{2a} $$
$$ x = \frac{7}{2⋅(-2)} = -\frac{7}{4} $$
Find the y-coordinate of the vertex by substituting the x-coordinate into the function.
f(x) = −2x2 − 7x − 4
$$ f\left(-\frac{7}{4}\right) = −2\left(-\frac{7}{4}\right)^2 − 7\left(-\frac{7}{4}\right) − 4 $$
$$ f\left(-\frac{7}{4}\right) = \frac{17}{8} = k $$
The a of the equation is less than 0, so the parabola opens down and the vertex is the maximum. The range is y ≤ k which would be \(y ≤ \frac{17}{8}\). In interval notation, the range is \(\left(-∞, \frac{17}{8}\right]\).
Find the domain and range of f(x) = x2 + 4x − 21.
Answer
Domain: (−∞, ∞); Range: [−25, ∞)
The graph of a quadratic function may have 0, 1, or 2 real x-intercepts. It will always have one y-intercept. The intercepts are useful for applications such as the path of a thrown ball. The x-intercepts would be the places where the ball hits the ground. The y-intercept would be the initial height of the ball.
The x-intercepts are the points where the graph intersects the x-axis and occur when y = 0. The y-intercept is the point where the graph intersects the y-axis and occurs when x = 0.
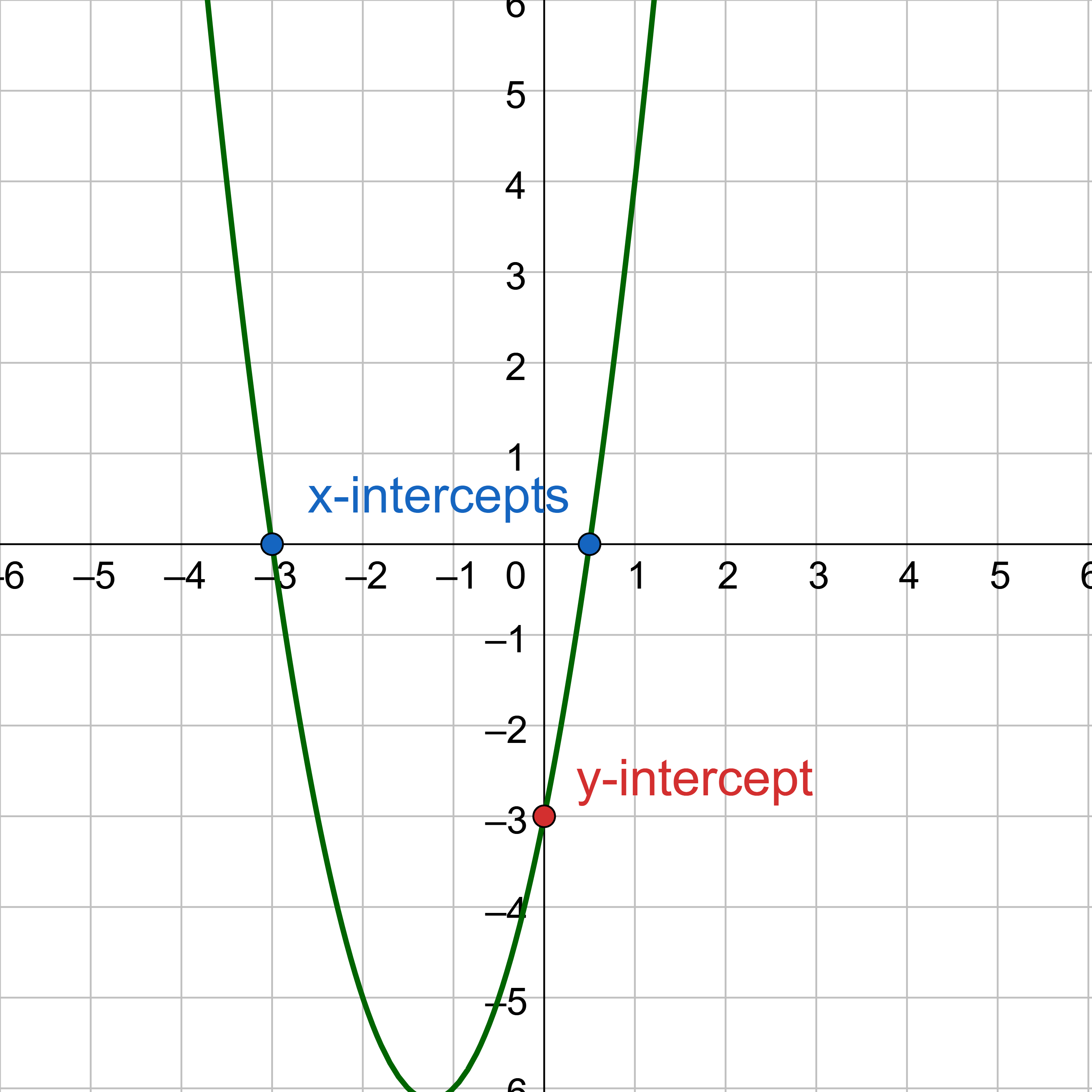
Find the x- and y-intercepts of f(x) = 2x2 + 5x − 3.
Solution
Find the x-intercepts by setting the function equal to zero and solving for x.
2x2 + 5x − 3 = 0
Factor or use the quadratic formula. Factoring is more efficient in this case.
(2x − 1)(x + 3) = 0
Set each factor equal to zero.
2x − 1 = 0 or x + 3 = 0
2x = 1 or x = −3
\(x = \frac{1}{2}\) or x = −3
The x-intercepts are \(\left(\frac{1}{2}, 0\right)\) and (−3, 0).
Find the y-intercept by substituting x = 0 into the function.
f(x) = 2x2 + 5x − 3
f(0) = 2(0)2 + 5(0) − 3
f(0) = −3
The y-intercept is (0, −3). See the graph in figure 11.
In example 7, the quadratic equation used to find the x-intercepts was found by factoring. However, many quadratic equations are not factorable. Two techniques for solving quadratic equations other than factoring are rewriting in standard form and the quadratic formula.
Find the x-intercepts of the quadratic function f(x) = x2 – 4x – 1.
Solution
Find the x-intercepts by setting the function = 0 and solving for x
x2 – 4x – 1 = 0
Unfortunately, this is not easily factored, so rewrite it in standard form. Start by identifying a which is the leading coefficient. In this case a = 1.
Now, find the x-coordinate of the vertex.
$$ x = \frac{-b}{2a} $$
$$ x = \frac{-(-4)}{2(1)} = 2 $$
Because this is the vertex, h = 2. Substitute x = 2 into the function to find the y-coordinate of the vertex.
f(x) = x2 – 4x – 1
f(2) = 22 – 4(2) – 1 = −5
This is the y-coordinate of the vertex, so k = −5. Substitute a, h, and k into standard form.
f(x) = a(x − h)2 + k
f(x) = (x − 2)2 – 5
Now find the x-intercepts by setting the function = 0 and solving for x.
0 = (x − 2)2 – 5
5 = (x − 2)2
$$ ±\sqrt{5} = x - 2 $$
$$ 2 ± \sqrt{5} = x $$
The x-intercepts are \((2 + \sqrt{5}, 0)\) and \((2 - \sqrt{5}, 0)\).
Find the x-intercepts of f(x) = x2 – 6x + 6.
Answer
\((3 – \sqrt{3}, 0)\) and \((3 + \sqrt{3}, 0)\)
$$ x = \frac{-b ± \sqrt{b^2 - 4ac}}{2a} $$
Solve 4x2 − 12x − 11 = 0.
Solution
Another way to solve quadratic equations is to use the quadratic formula. Start by putting the quadratic into general form. This quadratic already is in general form.
Identify a, b, and c.
ax2 + bx + c = 0
4x2 − 12x − 11 = 0
a = 4, b = −12, and c = −11. Substitute those into the quadratic formula.
$$ x = \frac{-b ± \sqrt{b^2 - 4ac}}{2a} $$
$$ x = \frac{-(-12) ± \sqrt{(-12)^2 - 4(4)(-11)}}{2(4)} $$
$$ x = \frac{12 ± \sqrt{320}}{8} $$
$$ x = \frac{12 ± 8\sqrt{5}}{8} $$
Factor 4 in the numerator, then reduce the fraction.
$$ x = \frac{4\left(3 ± 2\sqrt{5}\right)}{8} $$
$$ x = \frac{3 ± 2\sqrt{5}}{2} $$
The solutions are \(x = \frac{3 + 2\sqrt{5}}{2}\) and \(x = \frac{3 - 2\sqrt{5}}{2}\).

A baseball is hit straight up at 140 feet per second. The height of the ball when it was hit was 4 feet. The height of the ball above the ground as a function of time can be modeled by h(t) = −16t2 + 140t + 4.
Solution
The ball reaches the maximum height at the vertex of the parabola. The x-variable in this problem is actually t for time. The question is asking for the time of the maximum height which is the x- (or t-) coordinate of the vertex.
$$ t = \frac{-b}{2a} $$
$$ t = \frac{-140}{2(-16)} $$
$$ t = 4.375 $$
The ball reaches the maximum height at 4.375 s after it was hit.
The maximum height of the ball is the y- (or h-) coordinate of the vertex. Substitute the t-coordinate of the vertex into the function to the height.
h(t) = −16t2 + 140t + 4
h(4.375) = −16(4.375)2 + 140(4.375) + 4
h(4.375) = 310.25
The maximum height of the ball is 310.25 feet.
When the ball hits the ground, its height will be zero. Set the function equal to zero and solve for t.
−16t2 + 140t + 4 = 0
Divide every term by 4 to make all the numbers smaller.
−4t2 + 35t + 1 = 0
This does not look easily factorable, so another method is needed. The quadratic formula is useful with a = −4, b = 35, and c = 1.
$$ x = \frac{-b ± \sqrt{b^2 - 4ac}}{2a} $$
$$ t = \frac{-35 ± \sqrt{(35)^2 - 4(-4)(1)}}{2(-4)} $$
$$ t = \frac{-35 ± 35.23}{-8} $$
t = −0.03, 8.78
Traveling back in time is not possible, so only the positive answer will be accepted. The ball hits the ground after 8.78 s.

An inept shot putter accidentally threw the ball straight up at 30 feet per second from a height of 7 feet. The ball's height above the ground can be modeled by h(t) = −16t2 + 30t + 7.
Answer
a. 0.94 seconds; b. 21.06 feet; c. 2.08 seconds
f(x) = ax2 + bx + c
Sometimes called the vertex form.
f(x) = a(x − h)2 + k
The domain of any quadratic function is all real numbers or (−∞, ∞).
The range of a quadratic function is
where k is the y-coordinate of the vertex.


$$ x = \frac{-b ± \sqrt{b^2 - 4ac}}{2a} $$
Helpful videos about this lesson.