Precalculus by Richard Wright
Precalculus by Richard Wright
Ask and it will be given to you; seek and you will find; knock and the door will be opened to you. For everyone who asks receives; the one who seeks finds; and to the one who knocks, the door will be opened. Matthew 7:7-8 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.5.3

In factories, the cost of making a product is dependent on the number of items, x, produced. In a particular factory, the cost is given by the equation C(x) = 125x + 2000. This indicates that each item costs $125 and there is a $2000 initial cost to set up the production floor. The average cost for producing x items is found by dividing the cost function by the number of items, x. The average cost function for this situation is
$$ f(x) = \frac{125x + 2000}{x} $$
Many other applications require finding averages in a similar way. Written without a variable in the denominator, this function will contain a negative integer power.
The last few lessons have been about polynomial functions which have non-negative integers for exponents. This lesson is about rational functions which have variables in the denominator.
Rational functions are like the one above in the introduction. In mathematics, rational means "ratio" or can be written as a fraction. Rational functions then are functions written as fractions of polynomial functions in the form \(f(x) = \frac{P(x)}{Q(x)}\) where P(x) and Q(x) are polynomial functions.
The graphs of rational functions are characterized by asymptotes. Asymptotes are lines that the curve approaches at the edges of the coordinate plane. Vertical asymptotes occur where the denominator of a rational function approaches zero. A rational function cannot cross a vertical asymptote because it would be dividing by zero. Horizontal asymptotes occur when the x-values get very large in the positive or negative direction. Horizontal asymptotes can be crossed. Slant asymptotes are similar to horizontal asymptotes but are slanted lines.
A vertical asymptote of a graph is a vertical line x = a where the graph tends toward positive or negative infinity as the inputs approach a.
A horizontal asymptote of a graph is a horizontal line y = b where the graph approaches the line as the inputs approach ∞ or –∞.
A slant asymptote of a graph is a slanted line y = mx + b where the graph approaches the line as the inputs approach ∞ or –∞.
The domain of a rational function cannot include a value that makes the denominator equal zero because that causes the function to be undefined. To find the domain of a rational function, set the denominator equal to zero and solve for x.
The domain of a rational function is all real numbers except those that cause the denominator to equal zero.
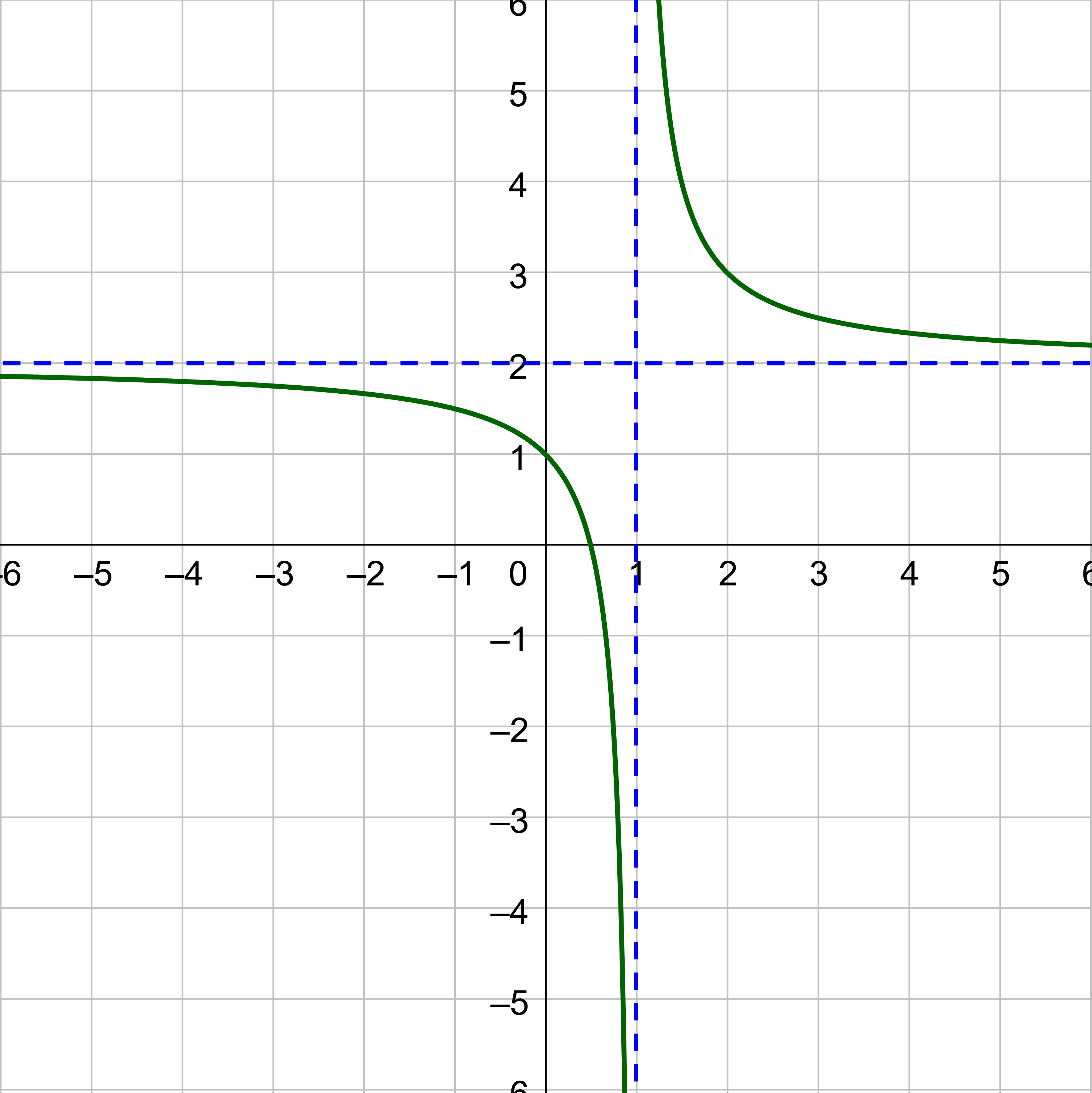
Find the domain of \(f(x) = \frac{x - 2}{x^2 - 4}\).
Solution
Set the denominator equal to zero and solve for x.
x2 – 4 = 0
x2 = 4
x = ±2
The domain of the function is all real numbers except x = ±2.
Analysis
The graph of this function in figure 3 shows that the function is not defined when x = ±2.
There is a vertical asymptote at x = –2 and a hole in the graph at x = 2.
Find the domain of \(f(x) = \frac{2x}{x^2 - 3x + 2}\).
Answer
The domain is all real numbers except x = 1 and x = 2.
Vertical asymptotes can be found from both the graph and from the function itself.
Vertical asymptotes come from the factors of the denominator that are not in common with a factor of the numerator. The vertical asymptotes occur where those factors equal zero.
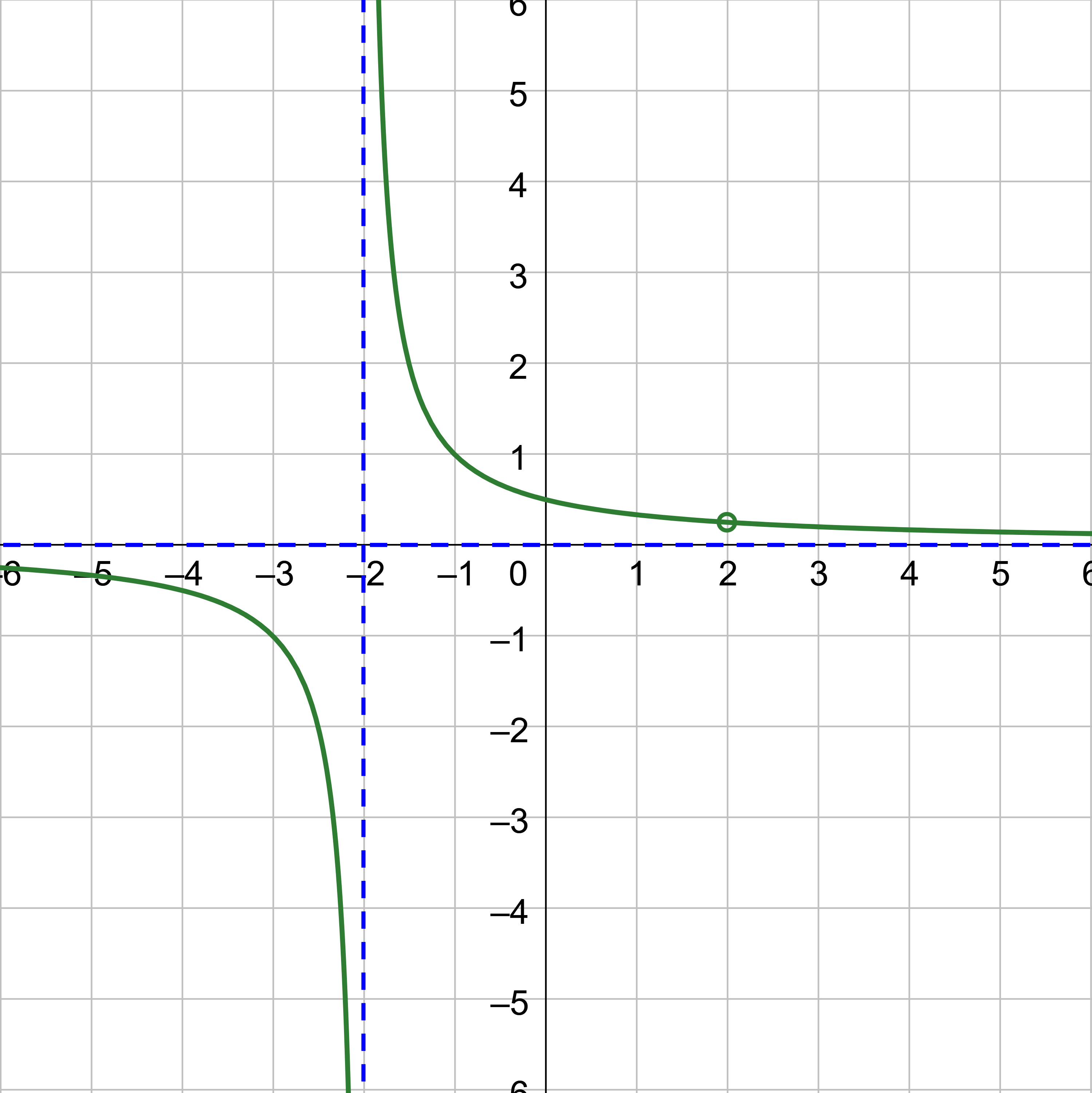
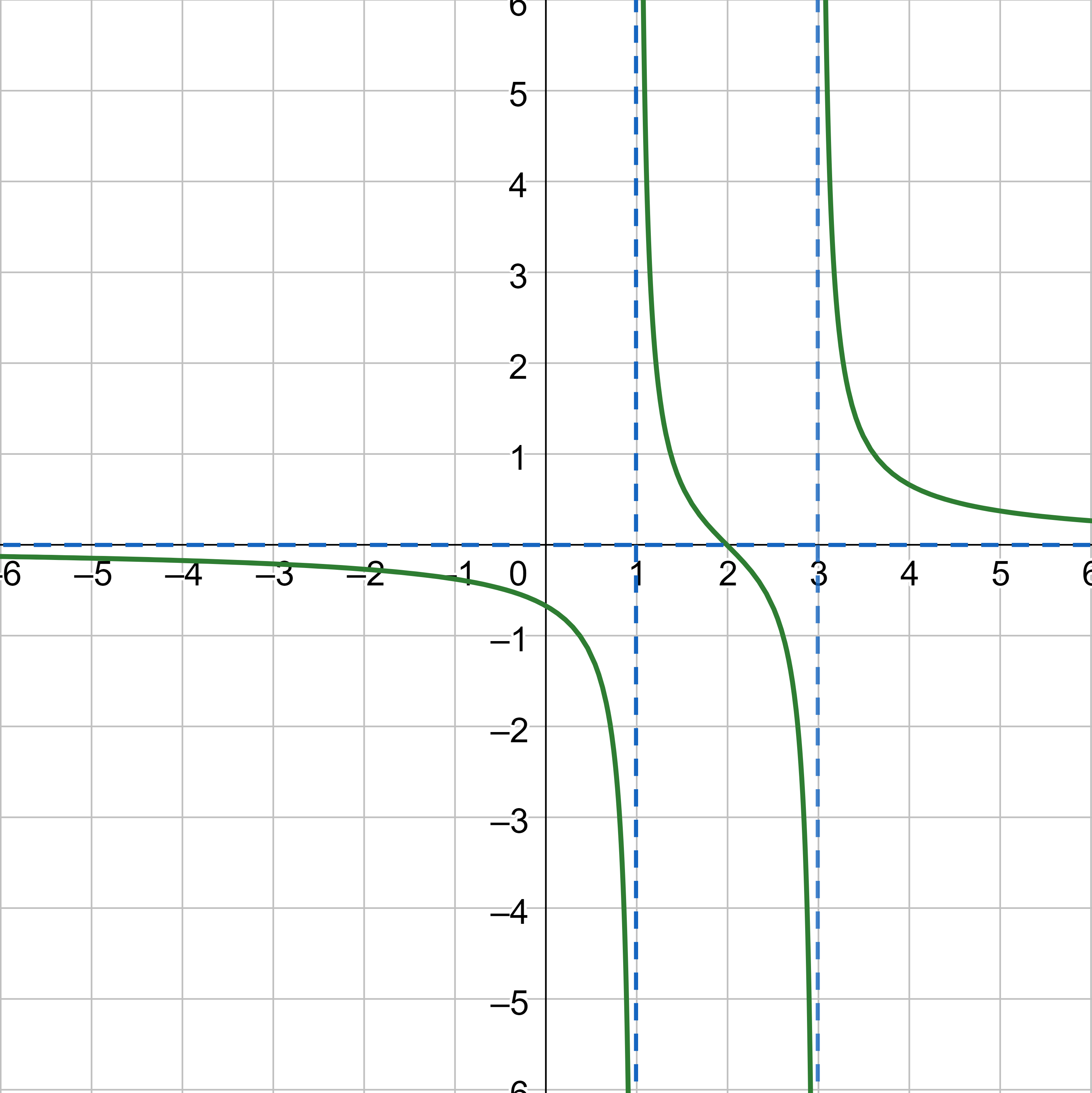
Find the vertical asymptotes of the graph of \(g(x) = \frac{x - 2}{x^2 - 4x + 3}\).
Solution
Start by factoring the numerator and denominator, if possible.
$$ \frac{(x - 2)}{(x - 3)(x - 1)} $$
Next, cancel any factors that are in both the numerator and denominator. In this example, there are no factors that cancel.
To find the vertical asymptotes, set the denominator equal to zero and solve for x.
(x − 3)(x − 1) = 0
This is already factored, so set each factor to zero and solve.
x − 3 = 0 or x − 1 = 0
x = 3 or x = 1
Since the asymptotes are lines, they are written as equations of lines. The vertical asymptotes are x = 3 and x = 1.
Sometimes a graph of a rational function will contain a hole. A hole is a single point where the graph is not defined and is indicated by an open circle. These holes come from the factors of the denominator that cancel with a factor of the numerator. When the function is simplified, the hole disappears. Thus, these types of holes are called removable discontinuities.
A removable discontinuity occurs in the graph of a rational function at x = a if a is a zero for a factor in the denominator that is common with a factor in the numerator.
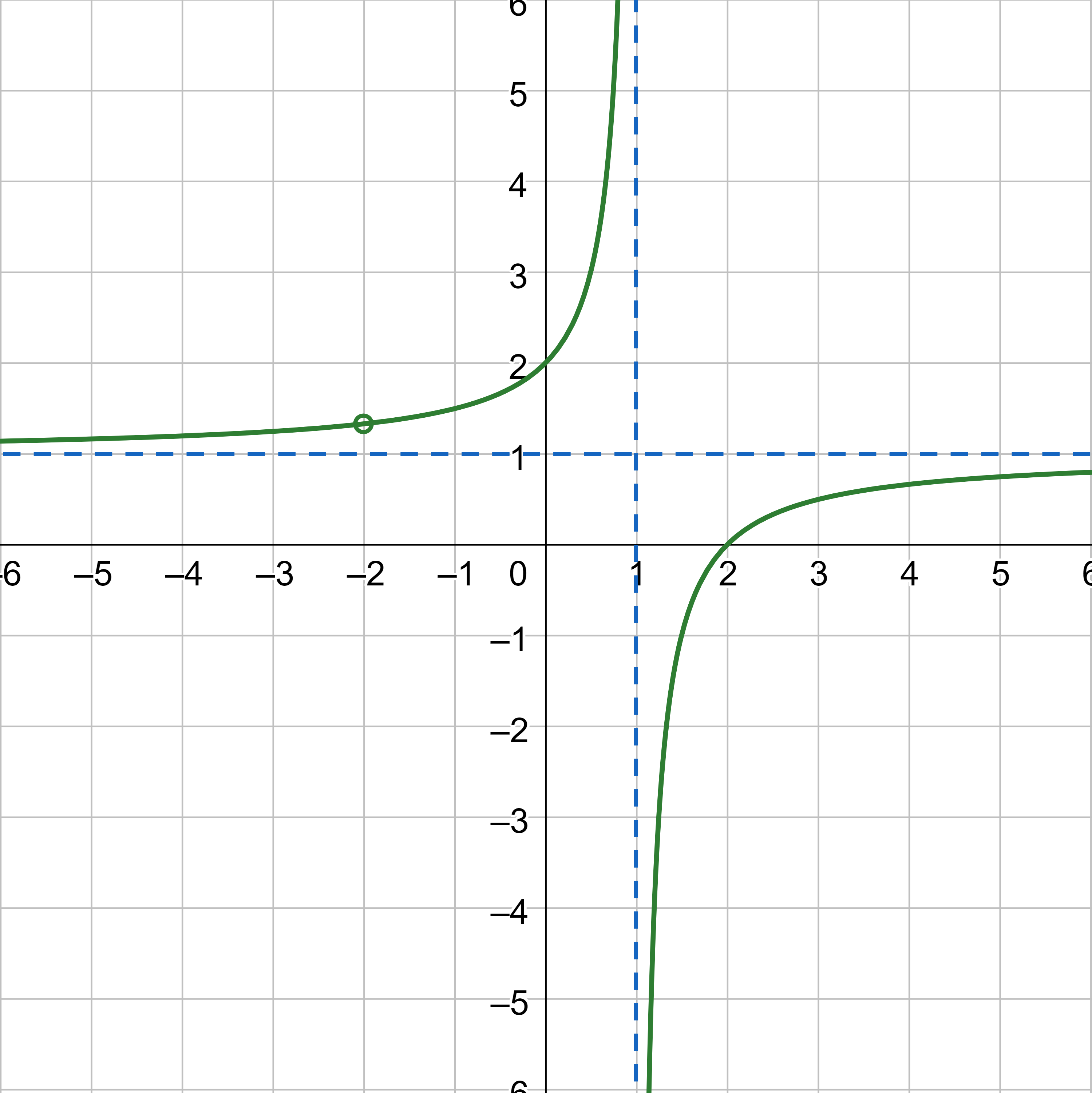
Find the vertical asymptotes and removable discontinuities of the graph of \(h(x) = \frac{x^2 - 4}{x^2 + x - 2}\).
Solution
Factor the numerator and the denominator.
$$ h(x) = \frac{(x - 2)(x + 2)}{(x - 1)(x + 2)} $$
Notice that there is a common factor in the numerator and the denominator, x + 2. The zero for this factor is x = −2. This is the location of the removable discontinuity.
Notice that there is a factor in the denominator that is not in the numerator, x − 1. The zero for this factor is x = 1. The vertical asymptote is x = 1.
Find the vertical asymptotes and removable discontinuities of the graph of \(f(x) = \frac{x^2 + 5x + 4}{x^2 - 3x - 4}\).
Answer
Removable discontinuity at x = −1. Vertical asymptotes: x = 4.
Vertical asymptotes describe the behavior of a graph as the output approaches ∞ or −∞. Horizontal asymptotes describe the behavior of a graph as the input approaches ∞ or −∞. Horizontal asymptotes can be found by substituting a large number (like 1,000,000) for x and estimating y.
There are three possibilities for horizontal asymptotes. Let N be the degree of the numerator and D be the degree of the denominator.
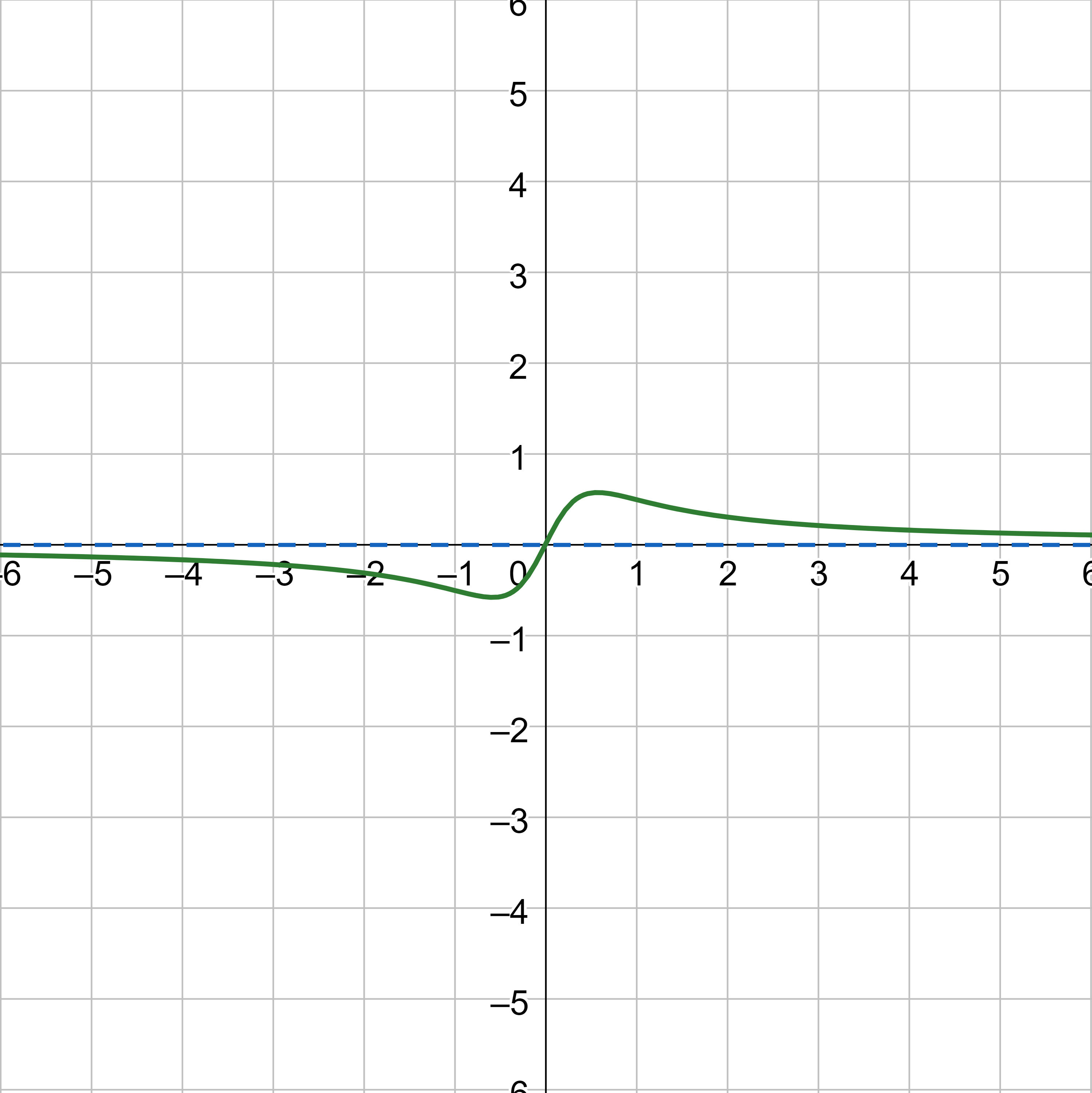
If N < D, then the horizontal asymptote is y = 0.
For example, \(y = \frac{2x}{3x^2 + 1}\). Substitute in a large number for x and estimate y.
$$ y = \frac{2(1000000)}{3(1000000)^2 + 1} $$
$$ y ≈ \frac{2000000}{3000000000000} ≈ 0 $$
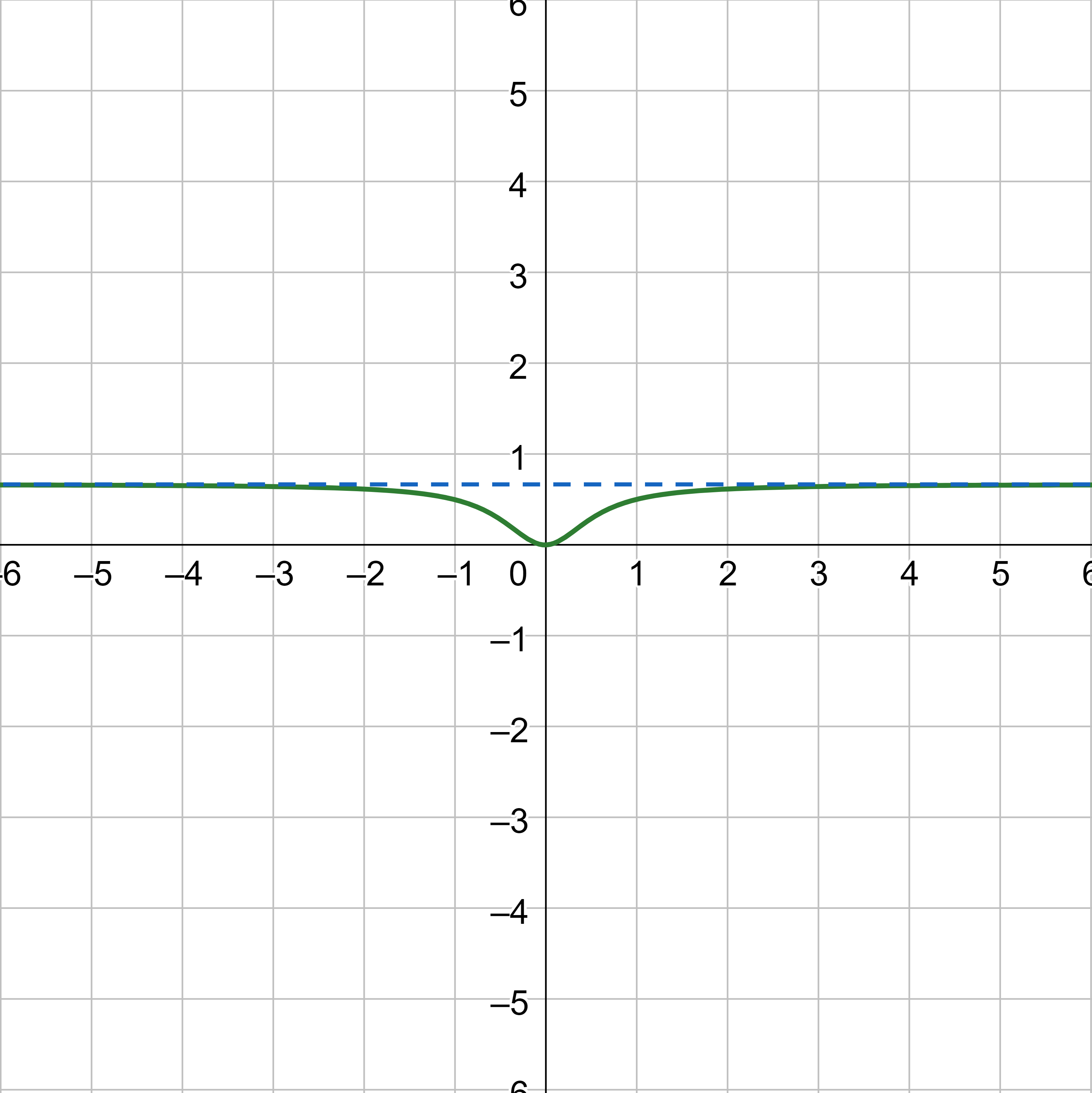
If N = D, then the horizontal asymptote is y = ratio of the leading coefficients.
For example, \(y = \frac{2x^2}{3x^2 + 1}\). Substitute in a large number for x and estimate y.
$$ y = \frac{2(1000000)^2}{3(1000000)^2 + 1} $$
$$ y ≈ \frac{2000000000000}{3000000000000} ≈ \frac{2}{3} $$
If N > D, then there is no horizontal asymptote.
For example, \(y = \frac{2x^2}{3x + 1}\). Substitute in a large number for x and estimate y.
$$ y = \frac{2(1000000)^2}{3(1000000) + 1} $$
$$ y ≈ \frac{2000000000000}{3000000} ≈ 666,667 $$
The y-value will get larger if a larger number was used for x, so no horizontal asymptote exists.
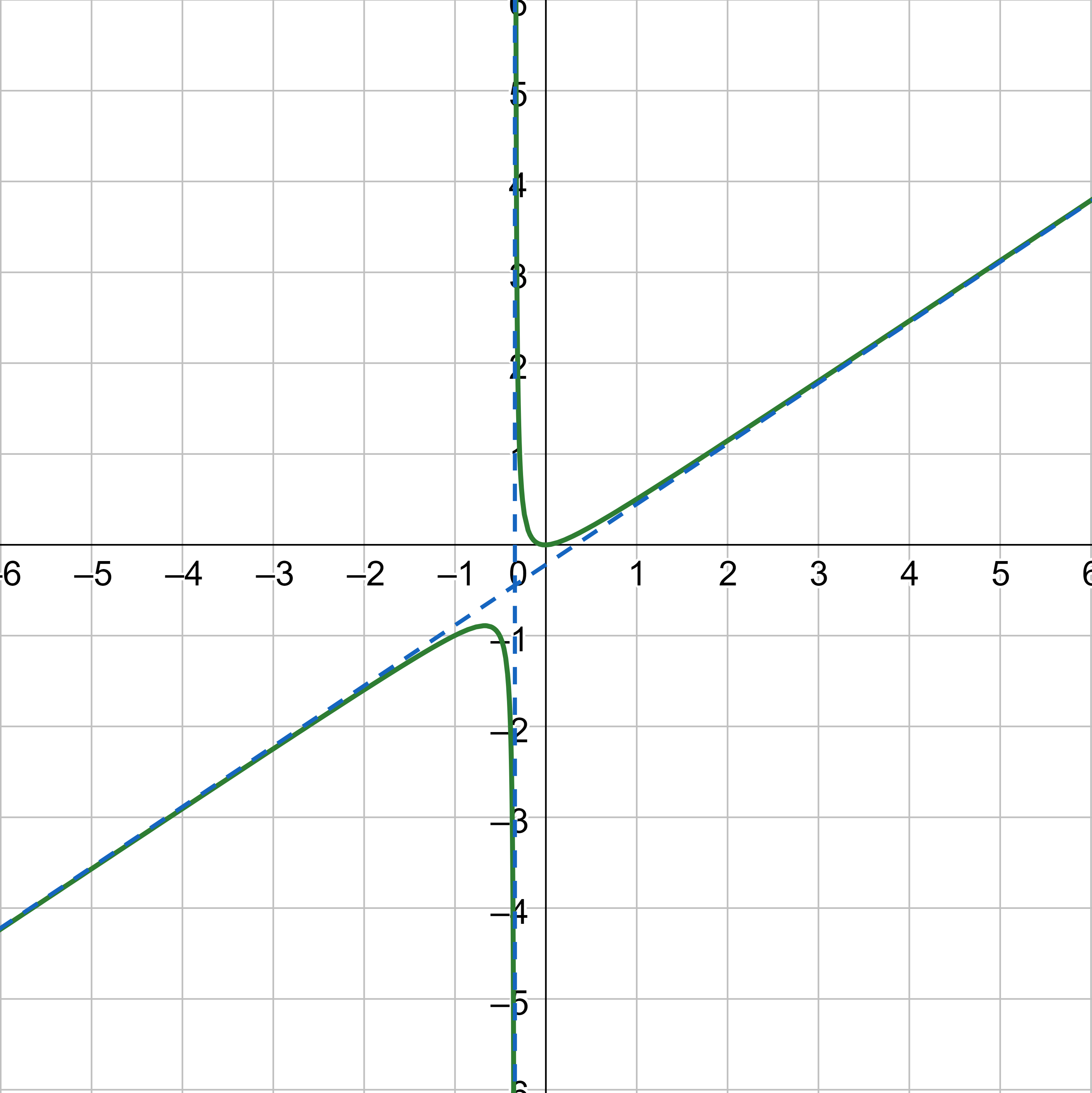
Slant asymptotes occur when the degree of the numerator is exactly one more than the degree of the denominator.
For example, \(y = \frac{2x^2}{3x + 1}\) has a slant asymptote because the numerator is degree 2 and the denominator is degree 1. To find the equation of the slant asymptote, divide the fraction and ignore the remainder. In this case, the quotient is \(y = \frac{2}{3}x - \frac{2}{9}\).

Notice that a graph of a rational function will never cross a vertical asymptote, but the graph may cross a horizontal or slant asymptote. Also, the graph of a rational function may have several vertical asymptotes, but the graph will have at most one horizontal or slant asymptote.
In general, if the degree of the numerator is larger than the degree of the denominator, the end behavior of the graph will be the same as the end behavior of the quotient of the rational fraction. For example, the function \(f(x) = \frac{x^3}{2x - 2}\) will have end behavior like a quadratic function because the quotient is a quadratic with the function is divided.
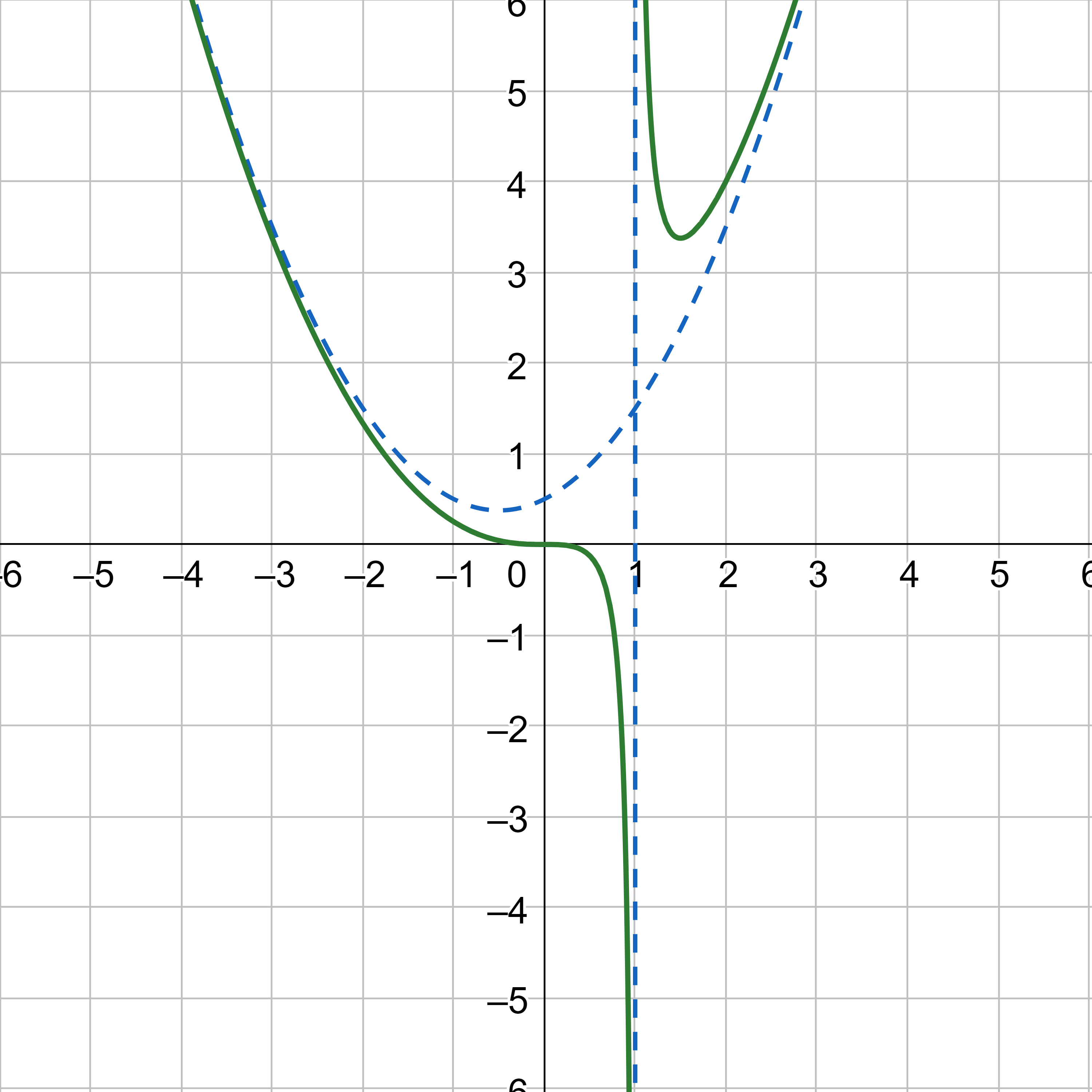
The horizontal asymptote of a rational function can be determined by looking at the degrees of the numerator and denominator.
If N is the degree of the numerator and D is the degree of the denominator, and…
The slant asymptote occurs when the degree of the numerator is 1 more than the degree of the denominator.
The slant asymptote is found by dividing the rational function and ignoring the remainder.
Identify the horizontal or slant asymptote.
Solution
For each of these, N = degree of the numerator and D = degree of the denominator.
N = 2 and D = 1. N > D, so there is no horizontal asymptote. However, there is a slant asymptote because N is 1 more than D. Find the slant asymptote by dividing the rational function and ignoring the asymptote.
| x | + | 1 | (2x² divided by 3x is 2x) | |||
| 2x + 1⟌ | 2x² | + | 3x | − | 1 | |
| −( | 2x² | + | x | ) | ↓ | (x multiplied by 2x + 1) |
| 2x | − | 1 | (Subtract. Bring down the next term. 2x divided by 2x is 1) | |||
| −( | 2x | + | 1) | (1 multiplied 2x + 1) | ||
| − | 2 | (Subtract. The remainder is −2) |
Ignore the remainder and the slant asymptote is the quotient. The slant asymptote is y = x + 1.
N = 2 and D = 2. N = D, so the horizontal asymptote is the ratio of the leading coefficients; \(y = \frac{1}{2}\).
N = 2 and D = 4. N < D, so the horizontal asymptote is y = 0.
The cost problem in the lesson introduction had the average cost equation \(f(x) = \frac{125x + 2000}{x}\). Find the horizontal asymptote and interpret it in context of the problem.
Solution
The degree of the numerator, N = 1 and the degree of the denominator, D = 1. N = D, so the horizontal asymptote is the ratio of the leading coefficients; \(y = \frac{125}{1} = 125\).
The horizontal asymptote describes what happens when the input increases without bound and approaches ∞. In this case the cost will approach 125. In the context of the problem, as more units are made, the cost approaches $125 each.
Find the horizontal and vertical asymptotes of the function \(y = \frac{(x+4)(x-2)}{(x+2)(x-1)(x-3)}\).
Solution
Conveniently, this is already factored. Notice that there are no common factors between the numerator and denominator, so there are no removable discontinuities.
Find the vertical asymptotes by setting the denominator equal to zero and solving for x.
(x + 2)(x − 1)(x − 3) = 0
Since it is factored, set each factor equal to zero and solve.
x + 2 = 0 or x − 1 = 0 or x − 3 = 0
x = −2 or x = 1 or x = 3
The vertical asymptotes are x = −2, x = 1, and x = 3.
To find the horizontal asymptotes, check the degrees of the numerator and denominator. Think of the result of multiplying the factors together. The numerator would be quadratic, so the degree is N = 2. The denominator would be cubic, so the degree is D = 3. N < D so the horizontal asymptote is y = 0.
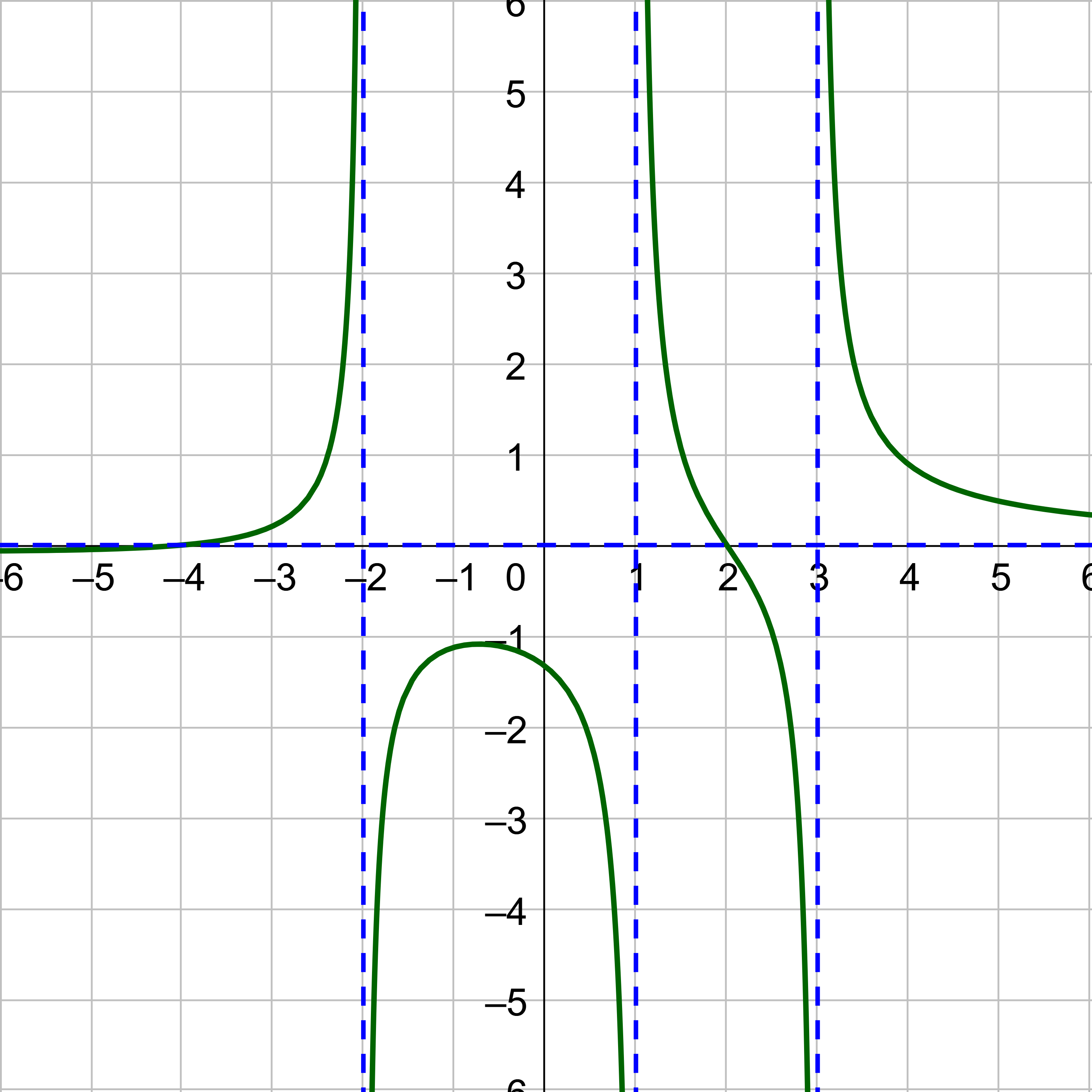
Find the vertical and horizontal asymptotes of the function \(y = \frac{(x + 2)(2x - 1)}{(x - 3)(x + 1)}\).
Answers
Vertical asymptotes at x = 3 and x = –1; horizontal asymptote at y = 2.
A vertical asymptote of a graph is a vertical line x = a where the graph tends toward positive or negative infinity as the inputs approach a.
A horizontal asymptote of a graph is a horizontal line y = b where the graph approaches the line as the inputs approach ∞ or –∞.
A slant asymptote of a graph is a slanted line y = mx + b where the graph approaches the line as the inputs approach ∞ or –∞.
The domain of a rational function is all real numbers except those that cause the denominator to equal zero.
A removable discontinuity occurs in the graph of a rational function at x = a if a is a zero for a factor in the denominator that is common with a factor in the numerator.
The horizontal asymptote of a rational function can be determined by looking at the degrees of the numerator and denominator.
If N is the degree of the numerator and D is the degree of the denominator, and…
The slant asymptote occurs when the degree of the numerator is 1 more than the degree of the denominator.
The slant asymptote is found by dividing the rational function and ignoring the remainder.
Helpful videos about this lesson.