Precalculus by Richard Wright
Precalculus by Richard Wright
Are not two sparrows sold for a penny? Yet not one of them will fall to the ground outside your Father’s care. And even the very hairs of your head are all numbered. So don’t be afraid; you are worth more than many sparrows. Matthew 10:29-31 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.6.2

A bakery makes decorated sheet cakes for birthday parties and other occasions. The bakery needs a certain volume because that is how much batter the recipe makes. However, they also want the size of the cake to have set proportions because it seems pleasing to the eye. This type of problem can be solved by creating a polynomial expression for volume.
The Rational Zero Theorem narrows the number of possible zeros of a polynomial function from an infinite number of choices to a few options. Then the possible rational zeros can be tested with synthetic division to see which are actually zeros.
Find the zeros of f(x) = 4x3 + 4x2 − 7x + 2.
Solution
Start by using the Rational Zero Theorem to find the list of possible rational zeros. The p's are factors of the constant term, 2.
p = ±1, ±2
The q's are factors of the leading coefficient, 4.
q = ±1, ±2, ±4
The possible rational zeros are in the form \(\frac{p}{q}\). Duplicates such as \(\frac{1}{2}\) and \(\frac{2}{4}\) have been removed from the list below.
$$ \frac{p}{q} = ±1, ±\frac{1}{2}, ±\frac{1}{4}, ±2 $$
Choose one of the possible rational zeros to test. Since real zeros are also x-intercepts of the graph of the function, use a graphing calculator to find an x-intercept that is in the list of possible rational zeros. Remember some real zeros will be irrational and not on the list.
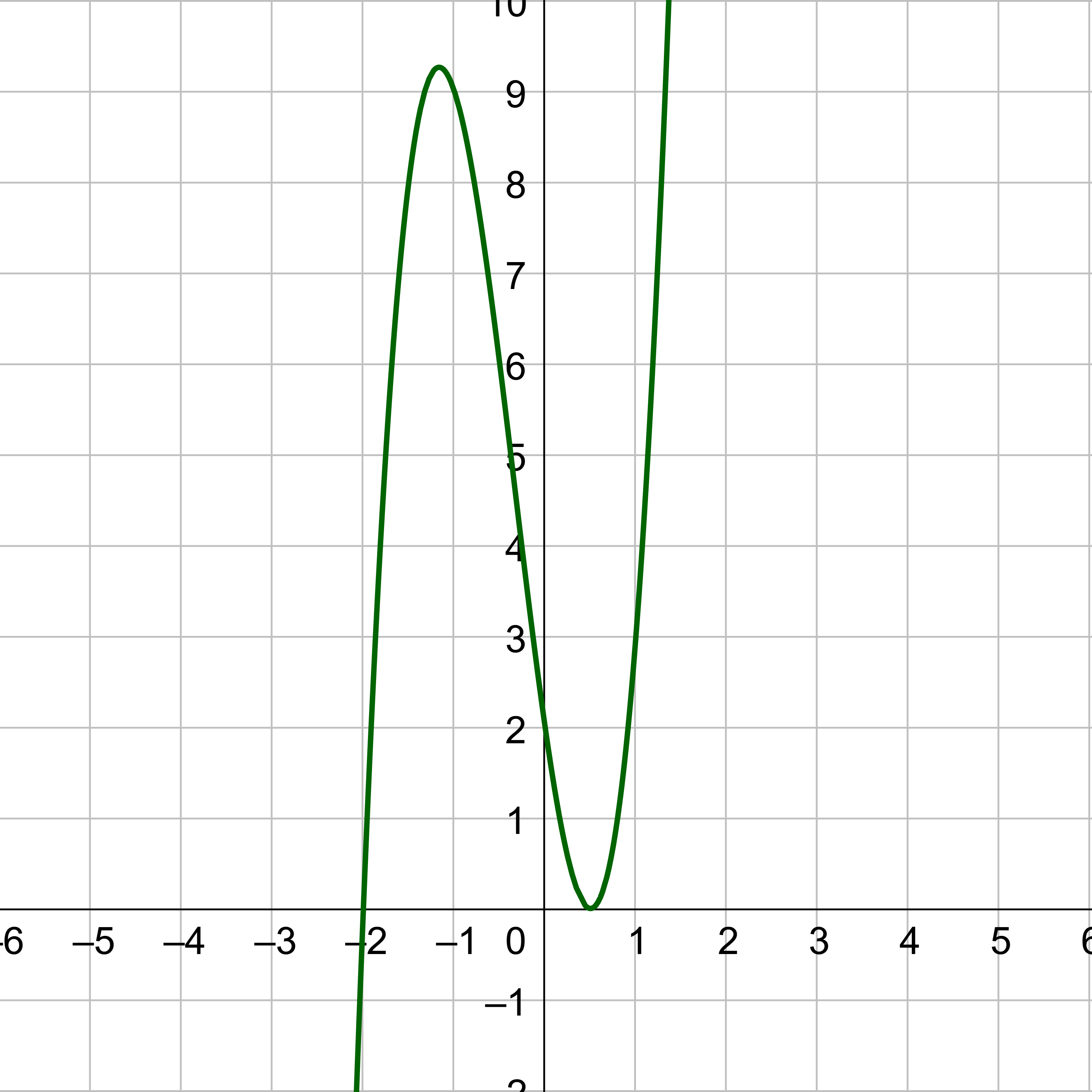
The graph shows an x-intercept at −2, so choose −2 as the first test point. Test it with synthetic division.
| −2 | 4 | 4 | −7 | 2 |
| −8 | 8 | −2 | ||
| 4 | −4 | 1 | 0 |
The remainder is zero, so that means −2 is a zero of the function. The depressed polynomial is one degree less than the original function, so the degree is now 2. The depressed polynomial is quadratic. Factor or use the quadratic formula to find the last two zeros. If the depressed polynomial was not quadratic, then it would be used with synthetic division and another possible zero.
4x2 − 4x + 1 = 0
(2x − 1)2 = 0
2x −1 = 0
$$ x = \frac{1}{2} $$
The factor (2x − 1) is squared which means it is in the function twice. Thus, its zero, \(\frac{1}{2}\) has multiplicity two. Notice that the graph in figure 2 crosses the x-axis at −2 which indicates odd multiplicity (1 in this case) and touches without crossing at \(\frac{1}{2}\) which indicates even multiplicity (2 in this case).
The zeros of f(x) are −2 and \(\frac{1}{2}\) with multiplicity 2.
After knowing how to find zeros of polynomial functions, the question is how many zeros should there be? The Fundamental Theorem of Algebra states that a polynomial function has at least one complex zero. However, the process of finding zeros involves dividing linear factors of the polynomial. Each time a factor is divided out, the degree of the depressed polynomial is reduced by one. Thus, we can divide a third-degree polynomial by three factors. This indicates that a nth degree polynomial function has n factors and, thus, n zeros.
If f(x) is a polynomial of degree n > 0, then f(x) has at least one complex zero.
More specifically, a polynomial has the same number of zeros as its degree.
Find the zeros of f(x) = 2x3 – 6x2 + x – 3.
Solution
This function is factorable by grouping, but this example will show how to solve it by using the Rational Zero Theorem.
Start by using the Rational Zero Theorem to find the list of possible rational zeros. The p's are factors of the constant term, –3.
p = ±1, ±3
The q's are factors of the leading coefficient, 2.
q = ±1, ±2
The possible rational zeros are in the form \(\frac{p}{q}\).
$$ \frac{p}{q} = ±1, ±\frac{1}{2}, ±3, ±\frac{3}{2} $$
Choose one of the possible rational zeros to test. Since real zeros are also x-intercepts of the graph of the function, use a graphing calculator to find an x-intercept that is in the list of possible rational zeros. Remember some real zeros will be irrational and not on the list.
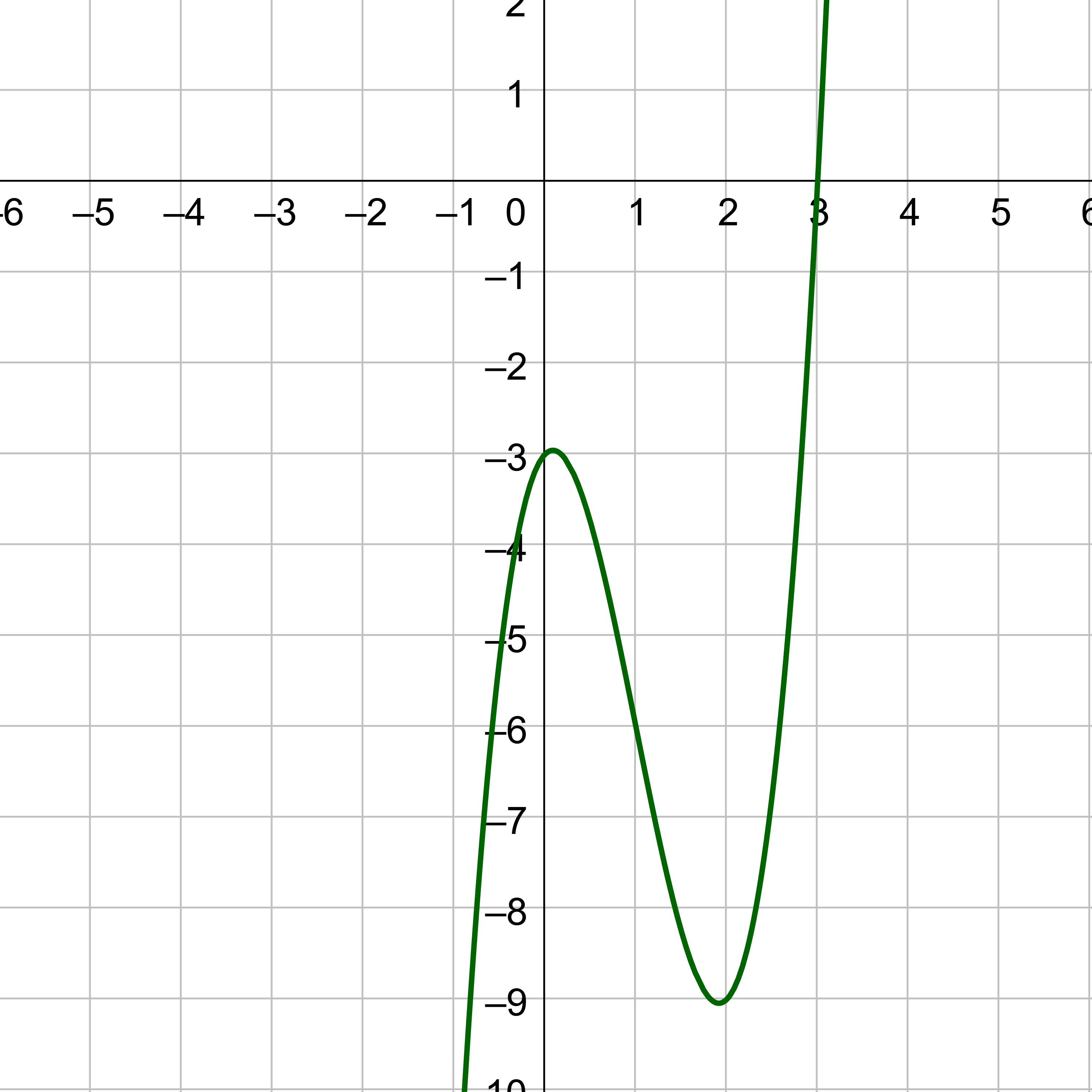
The graph shows an x-intercept at 3, so choose 3 as the first test point. Test it with synthetic division.
| 3 | 2 | −6 | 1 | −3 |
| 6 | 0 | 3 | ||
| 2 | 0 | 1 | 0 |
The remainder is zero, so that means 3 is a zero of the function. The depressed polynomial is one degree less than the original function, so the degree is now 2. The depressed polynomial is quadratic. Set the depressed polynomial equal to zero and solve to find the last two zeros. If the depressed polynomial was not quadratic, then it would be used with synthetic division and another possible zero.
2x2 + 1 = 0
2x2 = –1
$$ x^2 = -\frac{1}{2} $$
$$ x = ±\sqrt{-\frac{1}{2}} $$
$$ x = ±\frac{\sqrt{2}}{2}i $$
The last two zeros are imaginary. Notice that they are the same value, just positive and negative. Also notice that the graph in figure 3 shows the curve approaching the x-axis but curving away before it actually reaches the axis. This indicates two imaginary zeros.
The zeros of f(x) are 3 and \(±\frac{\sqrt{2}}{2}i\).
Find the zeros of f(x) = x3 – 3x2 + x + 5.
Answer
The zeros are –1, 2 ± i.
Another way to limit the list of possible real zeros of a polynomial function is to use Descartes' Rule of Signs. It uses the number of changes of sign in the coefficients of the function to determine the number of positive and negative real zeros. The function below has two sign changes.
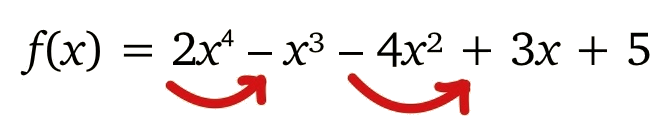
If f is a polynomial function with real coefficients, then
Use Descartes’ Rule of Signs to determine the possible numbers of positive and negative real zeros for f(x) = −3x4 + 5x3 + 2x2 − 3x + 1.
Solution
The number of positive real zeros is equal to the number of sign changes in the coefficients of f(x) or less than that by an even number. Figure 5 shows the number of sign changes in f(x).
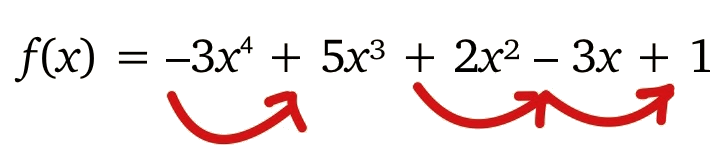
There are three sign changes in f(x), so there are 3 or 1 positive real zeros. The 1 is included because the number of real zeros is the number of sign changes or less by an even number. This is because there might be a pair of imaginary zeros. Essentially, this means the number of positive real zeros is the same as the number of sign changes and subtract by 2's until you reach 1 or 0.
The number of negative real zeros is equal to the number of sign changes in the coefficients of f(–x) or less by an even number. Substitute –x for x and simplify.
f(–x) = −3(–x)4 + 5(–x)3 + 2(–x)2 − 3(–x) + 1
f(–x) = −3x4 – 5x3 + 2x2 + 3x + 1

There is one change of sign in f(–x), so there is 1 negative real zero.
The Fundamental Theorem of Algebra says there are 4 total zeros because the degree is 4. The number of imaginary zeros can be found by subtracting the number of positive and negative zeros from the total 4.
| Positive Real Zeros | Negative Real Zeros | Imaginary Zeros | Total Zeros |
|---|---|---|---|
| 3 | 1 | 0 | 4 |
| 1 | 1 | 2 | 4 |
Analysis
A graph of the function confirms the number real zero. There is one negative x-intercept to correspond with the one negative real zero and one positive x-intercept for the positive real zero. There is a pair of imaginary zeros where the graph approaches the x-axis but does not touch it.
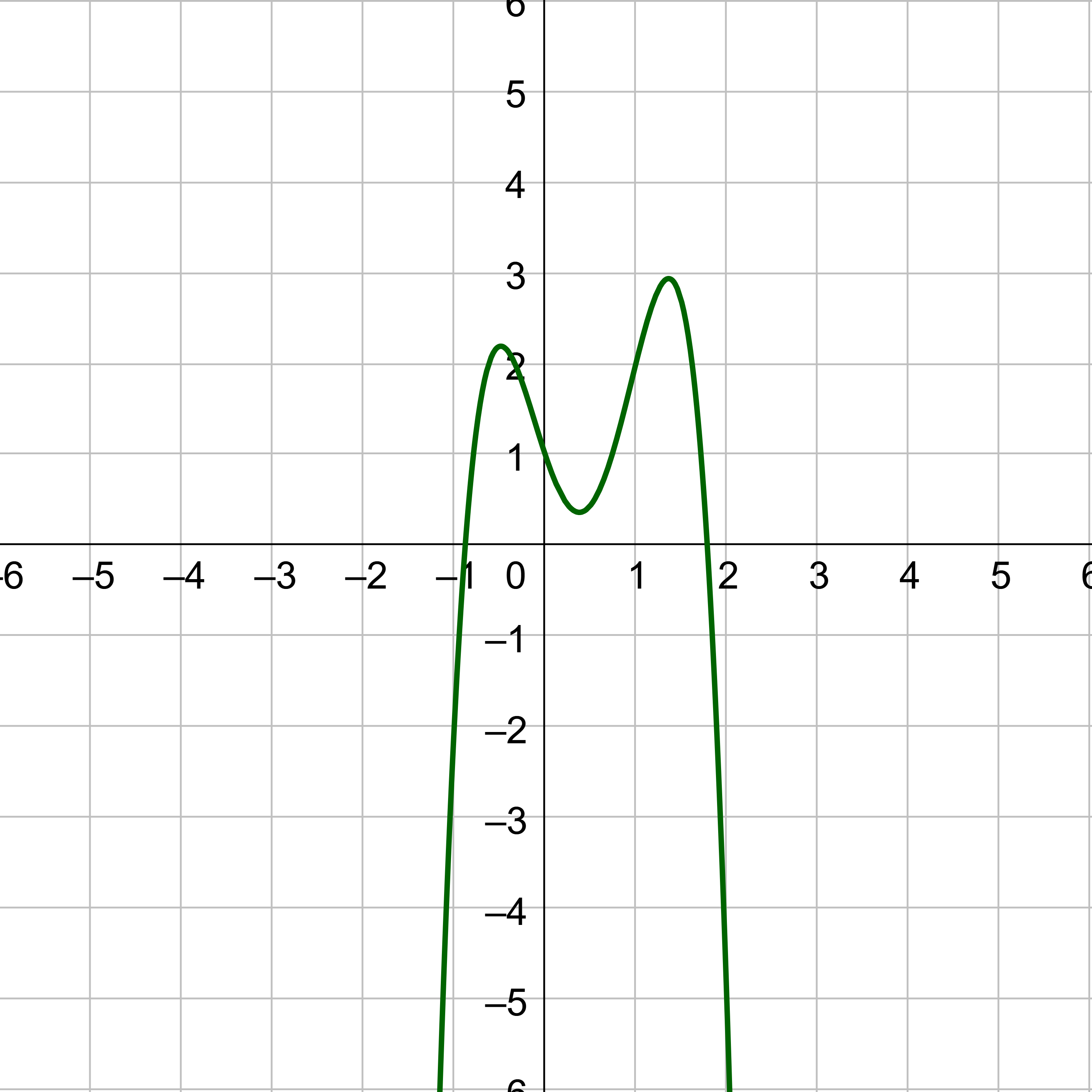
Use Descartes’ Rule of Signs to determine the maximum possible numbers of positive and negative real zeros for f(x) = –4x4 + 9x3 – 21x2 + 7x – 25. Use a graph to verify the numbers of positive and negative real zeros for the function.
Answer
There must be 4, 2, or 0 positive real zeros and 0 negative real zeros.
Another way to use the Fundamental Theorem of Algebra is to find a polynomial function with given zeros. The Linear Factorization Theorem states that if a zero of a polynomial is k, then a factor of the polynomial is (x – k). The polynomial can be found by multiplying all the factors together.
However, if one of the zeros is imaginary in the form a + bi, then a factor will be (x – (a + bi)). Multiplying out the factors will produce coefficients with i. To avoid that and have only real coefficients, then another zero will have to be a – bi and the corresponding factor (x – (a – bi)). Multiplying (x – (a + bi)) · (x – (a – bi)) results in only real coefficients. a + bi and a – bi are called complex conjugates which are complex numbers with the same real and imaginary parts, but the imaginary part has the opposite sign.
If the polynomial function f has real coefficients and a complex zero in the form a + bi, then the complex conjugate of the zero, a – bi, is also a zero.
Find a polynomial of least degree with real coefficients that has zeros of –1, 2, 3i, such that f(−2) = 208.
Solution
Because 3i is a zero, then –3i is also a zero. Write all the factors as (x – k) with a as the leading coefficient.
f(x) = a(x + 1)(x – 2)(x – 3i)(x + 3i)
Multiply the factors together to expand the polynomial. It is easiest to start by multiplying the factors with imaginary zeros first.
f(x) = a(x + 1)(x – 2)(x2 + 3ix – 3ix – 9i2)
Remember that i2 = –1.
f(x) = a(x + 1)(x – 2)(x2 + 9)
Continue multiplying the factors.
f(x) = a(x2 – x – 2)(x2 + 9)
f(x) = a(x4 – x3 + 7x2 – 9x – 18)
Substitute the point (–2, 208) to find a.
208 = a((–2)4 – (–2)3 + 7(–2)2 – 9(–2) – 18)
208 = a(52)
4 = a
Write the polynomial function by substituting a = 4 and distributing.
f(x) = 4(x4 – x3 + 7x2 – 9x – 18)
f(x) = 4x4 – 4x3 + 28x2 – 36x – 72
Find a third degree polynomial with real coefficients that has zeros of 1 and −4i such that f(2) = 60.
Answer
f(x) = 3x3 – 3x2 + 48x – 48
A new bakery offers decorated sheet cakes for children’s birthday parties and other special occasions. The bakery wants the volume of a small cake to be 756 cubic inches. The cake is in the shape of a rectangular solid. They want the length of the cake to be three inches longer than the width of the cake and the height of the cake to be two inches shorter than the width. What should the dimensions of the cake pan be?
Solution
Start by using the formula for the volume of a rectangular solid, V = ℓwh. In this case, ℓ = w + 3 and h = w – 2.
V = ℓwh
756 = (w + 3)w(w – 2)
756 = w3 + w2 – 6w
To solve the polynomial, set the equation equal to zero.
w3 + w2 – 6w – 756 = 0
This is not easily factored so use the Rational Zero Theorem to list the possible rational zeros. p is factors of the constant term, 756.
p = ±1, ±2, ±3, ±4, ±6, ±7, ±9, ±12, ±14, ±18, ±21, ±27, ±28, ±36, ±42, ±54, ±63, ±84, -±108, ±126, ±189, ±252, ±378, ±756
q is factors of the leading coefficient, 1. The list of \(\frac{p}{q}\) is then the same as p
\(\frac{p}{q}\) = ±1, ±2, ±3, ±4, ±6, ±7, ±9, ±12, ±14, ±18, ±21, ±27, ±28, ±36, ±42, ±54, ±63, ±84, -±108, ±126, ±189, ±252, ±378, ±756
Choose one of the possible rational zeros to test. Since real zeros are also x-intercepts of the graph of the function, use a graphing calculator to find an x-intercept that is in the list of possible rational zeros. Remember some real zeros will be irrational and not on the list.
The graph shows an x-intercept at 9, so choose 9 as the first test point. Test it with synthetic division.
| 9 | 1 | 1 | −6 | −756 |
| 9 | 90 | 756 | ||
| 1 | 10 | 84 | 0 |
The remainder is zero, so that means 9 is a zero of the function. The depressed polynomial is one degree less than the original function, so the degree is now 2. The depressed polynomial is quadratic. Set the depressed polynomial equal to zero and solve to find the last two zeros. If the depressed polynomial was not quadratic, then it would be used with synthetic division and another possible zero.
w2 + 10w + 84 = 0
This does not factor, so use the quadratic formula.
$$ w = \frac{-b ± \sqrt{b^2-4ac}}{2a} $$
$$ w = \frac{-10 ± \sqrt{10^2-4(1)(84)}}{2(1)} $$
$$ w = -5 ±\sqrt{59}i $$
The width of a cake must be real, so the only real solution is 9. The dimensions of the cake pan should be 12 in. × 9 in. × 7 in.
A shipping container in the shape of a rectangular solid must have a volume of 12 cubic meters. The client tells the manufacturer that, because of the contents, the length of the container must be one meter longer than the width, and the height must be two meters less than twice the width. What should the dimensions of the container be?
Answer
3 m × 2 m × 2 m
If f(x) is a polynomial of degree n > 0, then f(x) has at least one complex zero.
More specifically, a polynomial has the same number of zeros as its degree.
If f is a polynomial function with real coefficients, then
If the polynomial function f has real coefficients and a complex zero in the form a + bi, then the complex conjugate of the zero, a – bi, is also a zero.
Helpful videos about this lesson.