Precalculus by Richard Wright
Precalculus by Richard Wright
Anger is cruel and fury overwhelming, but who can stand before jealousy? Proverbs 27:4 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.6.2, PC.6.4

A landscape company is going to put some decorative rectangular prism-shaped stepping stones to make a path across a creek. Each stone will use 648 cubic inches of cement because that is convenient based on their cement supply. They decided that having a width six inches greater than the length is a pleasing proportion, and that the height should be one fourth the width for strength. What should be the dimensions of the stepping stone?
This problem can be solved by writing a cubic function and solving a cubic equation for the volume of the stepping stone. This lesson highlights a variety of tools for writing polynomial functions and solving polynomial equations.
The Remainder Theorem provides a convenient way to evaluate polynomials based on division. A polynomial may be evaluated at f(k) by dividing it by x − k. Synthetic division makes the process quick. Here is the proof of the theorem.
Remember that the Division Algorithm states that, given a polynomial dividend f(x) and a non-zero polynomial divisor d(x) where the degree of d(x) is less than or equal to the degree of f(x), there exist unique polynomials q(x) and r(x) such that
f(x) = d(x) q(x) + r(x)
Let the divisor be d(x) = x − k. Then the Division Algorithm becomes
f(x) = (x − k)q(x) + r
Since the divisor x − k is linear, the remainder will be a constant, r. And, if x = k, then
f(k) = (k − k)q(k) + r
= 0 · q(k) + r
= r
In other words, f(k) is the remainder obtained by dividing f(x) by x − k.
If a polynomial f(x) is divided by x − k, then the remainder is the value f(k).
Use the Remainder Theorem to evaluate f(x) = x4 − 2x3 − 3x2 + x − 11 at x = 3.
Solution
To use the Remainder Theorem, use synthetic division to divide the polynomial by x − 3.
| 3 | 1 | −2 | −3 | 1 | −11 |
| 3 | 3 | 0 | 3 | ||
| 1 | 1 | 0 | 1 | −8 |
The remainder is −8. Therefore, f(3) = −8.
Analysis
It is possible to check the answer by evaluating f(3).
f(x) = x4 − 2x3 − 3x2 + x − 11
f(3) = (3)4 − 2(3)3 − 3(3)2 + (3) − 11
= −8
Use the Remainder Theorem to evaluate f(x) = 3x5 − x4 − 2x3 + x2 + 3 at x = −1.
Answer
f(−1) = 2
The Factor Theorem tells how the zeros of a polynomial are related to the factors. Remember that the Division Algorithm tells us
f(x) = (x − k)q(x) + r.
If k is a zero, then the remainder, r, is f(k) = 0 and f(x) = (x − k)q(x) + 0 or f(x) = (x − k)q(x).
Notice, written in this form, x − k is a factor of f(x). So, if k is a zero of f(x), then x − k is a factor of f(x).
Similarly, if x − k is a factor of f(x), then the remainder of the Division Algorithm f(x) = (x − k)q(x) + r is 0. This tells that k is a zero.
This pair of statements is the Factor Theorem. It turns out that a polynomial of degree n in the complex number system will have n zeros. The Factor Theorem can be used to completely factor a polynomial into the product of n factors. Once the polynomial has been completely factored, its zeros can easily be found using the Zero Product Property.
According to the Factor Theorem, k is a zero of f(x) if and only if (x − k) is a factor of f(x).
Show that (x + 1) is a factor of x3 + 2x2 − 5x − 6. Find the remaining factors. Use the factors to determine the zeros of the polynomial.
Solution
Use synthetic division to show that (x + 1) is a factor of the polynomial.
| −1 | 1 | 2 | −5 | −6 |
| −1 | −1 | 6 | ||
| 1 | 1 | −6 | 0 |
The remainder is zero, so (x + 1) is a factor of the polynomial. The quotient is x2 + x − 6 which is a quadratic. Factor that quadratic.
x2 + x − 6 = (x − 2)(x + 3)
Now write all the factors of the polynomial as
(x + 1)(x − 2)(x + 3)
The Factor Theorem says that if x − k is a factor then k is a zero of the polynomial. Thus, the zeros of x3 + 2x2 − 5x − 6 are –1, 2, and −3.
Use the Factor Theorem to find the zeros of f(x) = x3 − 5x2 − 10x + 24 given that (x − 4) is a factor of the polynomial.
Answer
The zeros are −2, 3, and 4.
Another use for the Remainder Theorem is to test whether a rational number is a zero for a given polynomial. But first there needs to be a group of rational numbers to test. There are an infinite number of possible zeros to choose from. It would be nice to have fewer numbers to choose from. The Rational Zero Theorem narrows down the number of possible rational zeros using the ratio of the factors of the constant term and factors of the leading coefficient of the polynomial.
Think about a quadratic function with two zeros, \(x = \frac{2}{3}\) and \(x = \frac{4}{5}\). The Factor Theorem indicates that if a zero is k, then a factor is (x − k). If k is a fraction, then the factor can be found by setting x = k.
$$ x = \frac{2}{3}; x = \frac{4}{5} $$
Subtract to make these equal zero.
$$ x - \frac{2}{3} = 0; x - \frac{4}{5} = 0 $$
Multiply by the denominators to get rid of the fraction.
$$ 3x - 2 = 0; 5x - 4 = 0 $$
Multiply these together to make the quadratic function.
$$ \left(3x - 2\right)\left(5x - 4\right) $$
Multiply these together.
$$ 15x^2 - 22x + 8 $$
Notice that the leading coefficient and constant term can be factored.
$$ (3·5)x^2 - 22x + (2·4) $$
The zeros are made of ratios of the factors of the constant term to the factors of the leading coefficient: \(\frac{2}{3}\) and \(\frac{4}{5}\). This is true of all polynomials and is called the Rational Zero Theorem.
If the polynomial \(f(x) = a_{n}x^n + a_{n-1}x^{n-1} + \cdots + a_{1}x + a_0\) has integer coefficients, then every rational zero f(x) has the form of \(\frac{p}{q}\) where p is a factor of the constant term a0 and q is a factor of the leading coefficient an.
When the leading coefficient is 1, the possible rational zeros are the factors of the constant term.
The quotient that results from dividing a polynomial by a factor is called a depressed polynomial because it is one degree less than the original polynomial.
List all possible rational zeros of f(x) = 2x4 + 3x3 − 5x2 − 4.
Solution
The only possible rational zeros of f(x) are the ratios of the factors of the last term, –4, and the factors of the leading coefficient, 2.
Find the p's which are factors of the constant term, −4.
p = ±1, ±2, ±4.
Find the q's which are factors of the leading coefficient, 2.
q = ±1, ±2.
The rational zeros are the ratios of p to q.
$$ \frac{p}{q} = ±\frac{1}{1}, ±\frac{1}{2}, ±\frac{2}{1}, ±\frac{2}{2}, ±\frac{4}{1}, ±\frac{4}{2} $$
Notice that \(\frac{1}{1} = 1\) and \(\frac{4}{2} = 2\), which have already been listed. So, the list can be shortened.
$$ \frac{p}{q} = ±1, ±\frac{1}{2}, ±2, ±4 $$
Use the Rational Zero Theorem to find the rational zeros of f(x) = 4x3 + 8x2 − 31x + 4.
Solution
The Rational Zero Theorem says that the only possible rational zeros of f(x) are the ratios of the factors of the last term, 4, and the factors of the leading coefficient, 4.
Find the p's which are factors of the constant term, 4.
p = ±1, ±2, ±4.
Find the q's which are factors of the leading coefficient, 4.
q = ±1, ±2, ±4.
The rational zeros are the ratios of p to q.
$$ \frac{p}{q} = ±\frac{1}{1}, ±\frac{1}{2}, ±\frac{1}{4}, ±\frac{2}{1}, ±\frac{2}{2}, ±\frac{2}{4}, ±\frac{4}{1}, ±\frac{4}{2}, ±\frac{4}{4} $$
Simplifying and removing duplicates shortens the list to
$$ \frac{p}{q} = ±1, ±\frac{1}{2}, ±\frac{1}{4}, ±2, ±4 $$
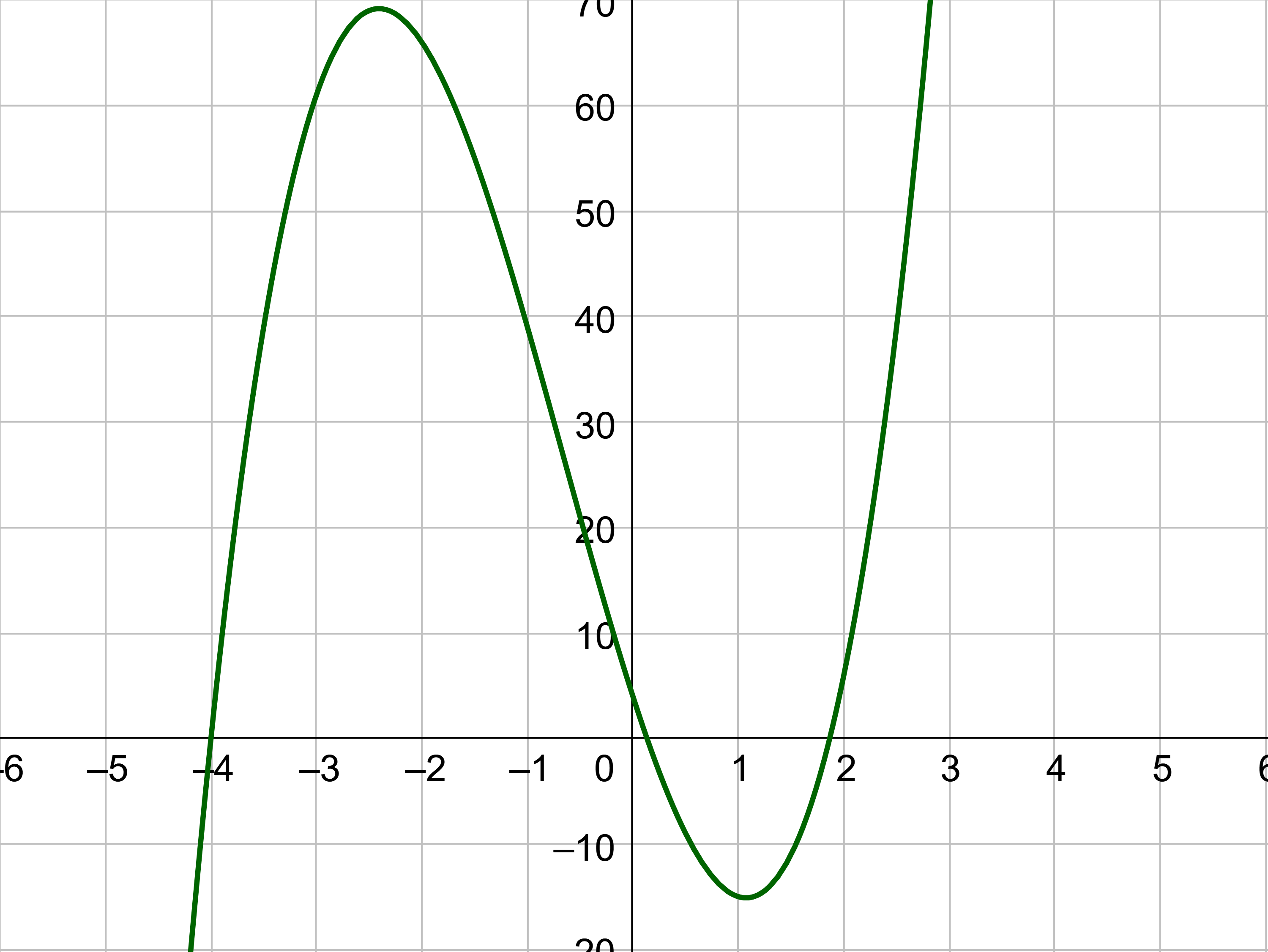
Choose one of the possible rational zeros to test. The graph in figure 2 indicates that −4 would be a good choice because that is an x-intercept, and x-intercepts are zeros. Start with x = −4.
| −4 | 4 | 8 | −31 | 4 |
| −16 | 32 | −4 | ||
| 4 | −8 | 1 | 0 |
The original function was degree 3. After dividing, the depressed polynomial is degree 2. The depressed polynomial is 4x2 − 8x + 1. Since this is quadratic, factor or use the quadratic formula to find the last two zeros. In this case, the quadratic does not factor, so use the quadratic formula.
$$ x = \frac{-b±\sqrt{b^2 - 4ac}}{2a} $$
$$ x = \frac{8 ± \sqrt{(-8)^2 - 4(4)(1)}}{2(4)} $$
$$ x = \frac{8 ± 4\sqrt{3}}{8} $$
$$ x = \frac{2 ± \sqrt{3}}{2} $$
The zeros are −4, \(\frac{2 + \sqrt{3}}{2}\), and \(\frac{2 - \sqrt{3}}{2}\). Notice the last two zeros are irrational, so the only rational zero is −4.
Use the Rational Zero Theorem to find the rational zeros of f(x) = x3 + 4x2 − 11x − 30.
Answer
−5, −2, 3
If a polynomial f(x) is divided by x − k, then the remainder is the value f(k).
According to the Factor Theorem, k is a zero of f(x) if and only if (x − k) is a factor of f(x).
If the polynomial \(f(x) = a_{n}x^n + a_{n-1}x^{n-1} + \cdots + a_{1}x + a_0\) has integer coefficients, then every rational zero f(x) has the form of \(\frac{p}{q}\) where p is a factor of the constant term a0 and q is a factor of the leading coefficient an.
When the leading coefficient is 1, the possible rational zeros are the factors of the constant term.
Helpful videos about this lesson.
| x | 1 | 3 | 5 | 7 |
|---|---|---|---|---|
| y | 1.5 | 0.5 | −0.5 | −1.5 |