Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Blessed are the merciful, for they will be shown mercy. Matthew 5:7 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.6.4
Solomon's Temple is described in detail in 1 Kings 6. The main sanctuary section is described as a rectangular prism with interior dimensions of 20 cubits wide, 60 cubits long, and 30 cubits high. The cubit is the distance from the elbow to the tips of the fingers on an average person. There were two different cubits in Old Testament times, the basic cubit of about 17.5 inches and the royal cubit which is about 20 inches. The longer royal cubit was likely used in this case making the interior dimensions of Solomon's Temple approximately 33 feet wide, 100 feet long, and 50 feet high. That is not very large compared to buildings today. My modest house is a rectangle about 25 feet wide by 100 feet long, or about the same footprint as the interior of the Temple! The interior volume of the Temple can be found using elementary geometry.
V = l ⋅ w ⋅ h
= (60 cubits) ⋅ (20 cubits) ⋅ (30 cubits)
= 36,000 cubits3
So, the interior volume of Solomon's Temple was 36,000 cubic cubits. What if only the volume, length, and width were known? We could divide to find the height.
$$ h = \frac{V}{l·w} $$
$$ = \frac{36,000 \text{ cubits}^3}{(60 \text{ cubits})(20 \text{ cubits})} $$
$$ = 30 \text{ cubits} $$
Just like stated above, the height is 30 cubits. But what if a model maker wants to print a scale model? He could build a digital scale model where the dimensions are given using variable terms. If he wants a certain size base and a certain volume, then he could use division to find the height using division with variables. This lesson focuses on how to divide polynomials with variables.
Long division with integers was taught in elementary school. The long division algorithm is divide the numbers on the left, multiply the answer with the divisor, subtract, bring down the next digit, and repeat until all the digits have been done. For example, consider dividing 137 by 3.
$$ \require{enclose} \begin{array}{rll} 45 \\ 3 \enclose{longdiv}{137} && \\ \underline{−12}\downarrow && \hbox{(\(3 × 4 = 12\))} \\ 17 && \hbox{(\(13 - 12 = 1\)), Bring down the 7} \\ \underline{-15} && \hbox{(\(3 × 5 = 15\))} \\ 2 && \hbox{(\(17 - 15 = 2\))} \\ && \hbox{Answer: 45 R 2 or \(45 \tfrac{2}{3}\)} \\ \end{array}$$
Another way to look at the solution is as a sum of parts. This should look familiar, since it is the same method used to check division in elementary arithmetic.
dividend = (divisor · quotient) + remainder
137 = (3 · 45) + 2
137 = 135 + 2
137 = 137
This is called the division algorithm and will be discussed more formally after looking at an example.
Division of polynomials is similar to long division of whole numbers. The terms of the polynomial division correspond to the digits (and place values) of the whole number division. For example, divide 3x3 − 2x2 + 5x + 1 by x + 1 using the long division algorithm, it would look like this:
Set up the division.
$$ \require{enclose} x + 1 \enclose{longdiv}{3x^3 - 2x^2 + 5x + 1} $$
3x2 divided by x.
$$ \require{enclose} \begin{array}{rl} \color{blue}{3x^2} \phantom{ + 10x + 4} \\ \color{blue}{x} + 1 \enclose{longdiv}{\color{blue}{3x^3} - 2x^2 + 5x + 1} \\ \end{array} $$
3x2 multiplied by x + 1.
$$ \require{enclose} \begin{array}{rl} \color{blue}{3x^2} \phantom{ + 10x + 4} \\ \color{blue}{x + 1} \enclose{longdiv}{3x^3 - 2x^2 + 5x + 1} \\ \color{blue}{3x^3 + 3x^2} \phantom{ + 10x + 4} \\ \end{array} $$
Subtract and bring down next term.
$$ \require{enclose} \begin{array}{rl} 3x^2 \phantom{ + 10x + 10} && \\ x + 1 \enclose{longdiv}{\color{blue}{3x^3 - 2x^2} + 5x + \phantom{0}1} \\ \underline{\color{blue}{-(3x^3 + 3x^2)}} \phantom{+} \downarrow \phantom{x + 4} \\ \color{blue}{-5x^2 + 5x} \phantom{0 + 4} \\ \end{array} $$
−5x2 divided by x.
$$ \require{enclose} \begin{array}{rl} 3x^2 \color{blue}{- 5x} \phantom{ + 100} \\ \color{blue}{x} + 1 \enclose{longdiv}{3x^3 - 2x^2 + 5x + \phantom{0}1} \\ \underline{-(3x^3 + 3x^2)} \phantom{+} \downarrow \phantom{x + 4} \\ \color{blue}{-5x^2} + 5x \phantom{0 + 4} \\ \end{array} $$
−5x multiplied by x + 1.
$$ \require{enclose} \begin{array}{rl} 3x^2 \color{blue}{- 5x} \phantom{ + 100} \\ \color{blue}{x + 1} \enclose{longdiv}{3x^3 - 2x^2 + 5x + \phantom{0}1} \\ \underline{-(3x^3 + 3x^2)} \phantom{+} \downarrow \phantom{x + 4} \\ -5x^2 + 5x \phantom{0 + 4} \\ \color{blue}{-5x^2 - 5x} \phantom{0 + 4} \\ \end{array} $$
Subtract and bring down next term.
$$ \require{enclose} \begin{array}{rl} 3x^2 - 5x \phantom{ + 100} \\ x + 1 \enclose{longdiv}{3x^3 - 2x^2 + 5x + \phantom{0}1} \\ \underline{-(3x^3 + 3x^2)} \phantom{+} \downarrow \phantom{x + 4} \\ \color{blue}{-5x^2 + 5x} \phantom{0 + 4} \\ \underline{\color{blue}{-(-5x^2 - 5x)}} \phantom{10} \downarrow \\ \color{blue}{10x + 1} \\ \end{array} $$
10x divided by x.
$$ \require{enclose} \begin{array}{rl} 3x^2 - 5x \color{blue}{ + 10} \\ \color{blue}{x} + 1 \enclose{longdiv}{3x^3 - 2x^2 + 5x + \phantom{0}1} \\ \underline{-(3x^3 + 3x^2)} \phantom{+} \downarrow \phantom{x + 4} \\ -5x^2 + 5x \phantom{0 + 4} \\ \underline{-(-5x^2 - 5x)} \phantom{10} \downarrow \\ \color{blue}{10x} + 1 \\ \end{array} $$
10 multiplied by x + 1.
$$ \require{enclose} \begin{array}{rl} 3x^2 - 5x \color{blue}{ + 10} \\ \color{blue}{x + 1} \enclose{longdiv}{3x^3 - 2x^2 + 5x + \phantom{0}1} \\ \underline{-(3x^3 + 3x^2)} \phantom{+} \downarrow \phantom{x + 4} \\ -5x^2 + 5x \phantom{0 + 4} && \\ \underline{-(-5x^2 - 5x)} \phantom{10} \downarrow \\ 10x + \phantom{0}1 \\ \color{blue}{10x + 10} \\ \end{array} $$
Subtract.
$$ \require{enclose} \begin{array}{rl} \color{red}{3x^2 - 5x + 10} \\ \color{purple}{x + 1} \enclose{longdiv}{3x^3 - 2x^2 + 5x + \phantom{0}1} \\ \underline{-(3x^3 + 3x^2)} \phantom{+} \downarrow \phantom{x + 4} \\ -5x^2 + 5x \phantom{0 + 4} \\ \underline{-(-5x^2 - 5x)} \phantom{10} \downarrow \\ \color{blue}{10x + \phantom{0}1} \\ \underline{\color{blue}{-(10x + 10)}} \\ \color{blue}{-9} \\ \end{array}$$
Answer: \(\color{red}{3x^2 - 5x + 10} \color{blue}{-} \frac{\color{blue}{9}}{\color{purple}{x + 1}}\)
This example found
$$ \frac{3x^3 - 2x^2 + 5x + 1}{x+ 1} = 3x^2 - 5x + 10 - \frac{9}{x + 1} $$
or by multiplying both sides by x + 1
3x3 − 2x2 + 5x + 1 = (x + 1)·(3x2 − 5x + 10) − 9
We can identify the dividend, the divisor, the quotient, and the remainder.
$$ \begin{array}{cccc} \color{blue}{3x^3 - 2x^2 + 5x + 1} & = \color{red}{(x + 1)} & · & \color{purple}{(3x^2 - 5x + 10)} & \color{green}{-9} \\ \color{blue}{\text{Dividend}} & \color{red}{\text{Divisor}} && \color{purple}{\text{Quotient}} & \color{green}{\text{Remainder}} \end{array} $$
Writing the result in this manner illustrates the Division Algorithm.
Given a polynomial dividend f(x) and a non-zero polynomial divisor d(x) where the degree of d(x) is less than or equal to the degree of f(x) there exist unique polynomials q(x) and r(x) such that
f(x) = d(x)·q(x) + r(x)
where q(x) is the quotient and r(x) is the remainder. The remainder is either equal to zero or has degree strictly less than d(x).
If r(x) = 0, then d(x) divides evenly into f(x). This means that both d(x) and q(x) are factors of f(x).
Divide 3x2 + 4x − 39 by x − 3.
Solution
Set up the division.
$$ \require{enclose} \begin{array}{rl} x - 3 \enclose{longdiv}{3x^2 + 4x - 39} \\ \end{array} $$
3x2 divided by x.
$$ \require{enclose} \begin{array}{rl} \color{blue}{3x} \phantom{ + 100} \\ \color{blue}{x} - 3 \enclose{longdiv}{\color{blue}{3x^2} + 4x - 39} \\ \end{array} $$
3x multiplied by x − 3.
$$ \require{enclose} \begin{array}{rl} \color{blue}{3x} \phantom{ + 100} \\ \color{blue}{x - 3} \enclose{longdiv}{3x^2 + 4x - 39} \\ \color{blue}{3x^2 - 9x} \phantom{ + 100} \\ \end{array} $$
Subtract and bring down next term.
$$ \require{enclose} \begin{array}{rl} 3x \phantom{ + 100} \\ x - 3 \enclose{longdiv}{\color{blue}{3x^2 + 4x} - 39} \\ \underline{\color{blue}{-(3x^2 - 9x)}} \phantom{+0} \downarrow \\ \color{blue}{13x - 39} \\ \end{array} $$
13x divided by x.
$$ \require{enclose} \begin{array}{rl} 3x \color{blue}{+ 13} \\ \color{blue}{x} - 3 \enclose{longdiv}{3x^2 + 4x - 39} \\ \underline{-(3x^2 - 9x)} \phantom{+0} \downarrow \\ \color{blue}{13x} - 39 \\ \end{array} $$
13 multiplied by x − 3.
$$ \require{enclose} \begin{array}{rl} 3x \color{blue}{+ 13} \\ \color{blue}{x - 3} \enclose{longdiv}{3x^2 + 4x - 39} \\ \underline{-(3x^2 - 9x)} \phantom{+0} \downarrow \\ 13x - 39 \\ \color{blue}{13x - 39} \\ \end{array} $$
Subtract.
$$ \require{enclose} \begin{array}{rl} \color{red}{3x + 13} \\ \color{purple}{x - 3} \enclose{longdiv}{3x^2 + 4x - 39} \\ \underline{-(3x^2 - 9x)} \phantom{+0} \downarrow \\ \color{blue}{13x - 39} \\ \underline{\color{blue}{-(13x - 39)}} \\ \color{blue}{0} \\ \end{array}$$
The quotient is 3x + 13. The remainder is 0. Write the result as
$$ \frac{3x^2 + 4x - 39}{x - 3} = 3x + 13 $$
or
3x2 + 4x − 39 = (x − 3)(3x + 13)
Analysis: The remainder is 0. This means that the dividend is divided evenly by the divisor, and that both the divisor and quotient are factors of the dividend.
Divide 6x3 + 7x2 − 9x + 3 by 3x − 1.
Solution
$$ \require{enclose} \begin{array}{rll} 2x^2 + 3x - 2 && (6x^3 \text{ divided by } 3x \text{ is } 2x^2)\\ 3x - 1 \enclose{longdiv}{6x^3 + 7x^2 - 9x + 2} && \\ \underline{-(6x^3 - 2x^2)} \phantom{+} \downarrow \phantom{ 0000} && (\text{Multiply } 3x - 1 \text{ by } 2x^2)\\ 9x^2 - 9x \phantom{0 + 4} && (\text{Subtract. Bring down the next term. } 9x^2 \text{ divided by } 3x \text{ is } 3x)\\ \underline{-(9x^2 - 3x)} \phantom{10} \downarrow && (\text{Multiply } 3x - 1 \text{ by } 3x)\\ -6x + 2 \phantom{)} && (\text{Subtract. Bring down the next term. } -6x \text{ divided by } 3x \text{ is } -2)\\ \underline{-(-6x + 3)} && (\text{Multiply } 3x - 1 \text{ by } -2)\\ -1 && (\text{Subtract. The remainder is } -1) \\ \end{array}$$
The remainder is −1. The result can be written as:
$$ \frac{6x^3+7x^2-9x + 2}{3x - 1}=2x^2 + 3x - 2 + \frac{-1}{3x - 1} $$
Analysis Check your work by using the Division Algorithm to rewrite the solution. Then multiply.
6x3 + 7x2 − 9x + 2 = (3x − 1)(2x2 + 3x − 2) − 1
Notice from the Division Algorithm,
Divide (2x3 + 7x2 − x − 2) ÷ (x2 + 3x − 2).
Solution
$$ \require{enclose} \begin{array}{rll} 2x + 1 && (2x^3 \text{ divided by } x^2 \text{ is } 2x)\\ x^2 + 3x - 2 \enclose{longdiv}{2x^3 + 7x^2 - 2x - 4\phantom{)}} && \\ \underline{-(2x^3 + 6x^2 - 4x)} \phantom{1} \downarrow \phantom{)} && (\text{Multiply } x^2 + 3x - 2 \text{ by } 2x)\\ x^2 + 2x - 4\phantom{)} && (\text{Subtract. Bring down the next term. } x^2 \text{ divided by } x^2 \text{ is } 1)\\ \underline{-(x^2 + 3x - 2)} && (\text{Multiply } x^2 + 3x - 2 \text{ by } 1)\\ -x - 2 && (\text{Subtract. The remainder is } -x - 2) \\ \end{array}$$
The remainder is −x − 2. The result can be written as:
$$ \frac{2x^3 + 7x^2 - 2x - 4}{x^2 + 3x - 2} = 2x + 1 + \frac{-x - 2}{x^2 + 3x - 2} $$
Analysis Check your work by using the Division Algorithm to rewrite the solution. Then multiply.
2x3 + 7x2 − 2x − 4 = (x2 + 3x − 2)(2x + 1) + (−x − 2)
Notice from the Division Algorithm,
Divide (2x3 + 13x2 + x − 23) ÷ (2x + 3).
Answer
\(x^2 + 5x - 7 + \frac{-2}{2x + 3}\)
As is evident from the previous examples, long division can be long and cumbersome. Synthetic Division is a shorthand method of dividing polynomials by a binomial, x − k. Notice the leading coefficient of the binomial is 1.
To illustrate the process, recall the example at the beginning of the section.
Divide 3x3 − 2x2 + 5x + 1 by x + 1 using long division. The final form of the process looked like this:
$$ \require{enclose} \begin{array}{rll} 3x^2 - 5x + 10 && \\ x + 1 \enclose{longdiv}{3x^3 - 2x^2 + 5x + \phantom{0}1} && \\ \underline{-(3x^3 + 3x^2)} \phantom{+} \downarrow \phantom{x + 4} && \\ -5x^2 + 5x \phantom{0 + 4} && \\ \underline{-(-5x^2 - 5x)} \phantom{10} \downarrow && \\ 10x + \phantom{0}1 && \\ \underline{-(10x + 10)} && \\ -9 && \\ \end{array}$$
There is a lot of repetition in the table. To simplify it, don’t write the variables, but line up their coefficients in columns under the division sign. Also, eliminate the partial products to create a simpler version of the entire problem.
$$ \require{enclose} \begin{array}{rll} 3 \quad -5 \quad\quad 10 && \\ 1 \enclose{longdiv}{3 \quad -2 \quad\quad 5 \quad\quad \phantom{0}1} && \\ \underline{-3 \quad -3}\quad \phantom{+} \downarrow \phantom{000}\quad && \\ \underline{5 \quad\quad 5} \phantom{10} \quad \downarrow && \\ \underline{-10 \; -10} && \\ -9 && \\ \end{array}$$
Synthetic division further simplifies even more steps. Collapse the table by moving each of the rows up to fill any vacant spots. Also, instead of dividing by 1, as is done in division of whole numbers, then multiplying and subtracting the middle product, change the sign of the “divisor” to –1, multiply and add. The process starts by bringing down the leading coefficient.
$$ \begin{array}{rrrrr} \underline{-1}| & 3 & -2 & 5 & 1 \\ & & -3 & 5 & -10 \\ \hline & 3 & -5 & 10 & |\underline{-9} \end{array} $$
Then multiply it by the “divisor” and add, repeating this process column by column, until there are no entries left. The bottom row represents the coefficients of the quotient; the last entry of the bottom row is the remainder. In this case, the quotient is 3x2 − 5x + 10 and the remainder is −9. The process will be made more clear in example 4.
Synthetic division is a shortcut that can be used when the divisor is a binomial in the form x − k. In synthetic division, only the coefficients are used in the division process.
Use synthetic division to divide 3x2 + 5x − 20 by x + 2.
Solution
Begin by setting up the synthetic division. The binomial divisor is x + 2, so k is −2. Write k and the coefficients.
$$ \begin{array}{rrrr} \underline{-2}| & 3 & 5 & -20 \\ \end{array} $$
Bring down the leading coefficient. Multiply the leading coefficient by k and write the result in the next column.
$$ \begin{array}{rrrr} \underline{-2}| & 3 & 5 & -20 \\ & & -6 & & \\ \hline & 3 & & & \end{array} $$
Next, add the numbers in the second column. Multiply the resulting number by k. Write the result in the next column. Then add the numbers in the third column.
$$ \begin{array}{rrrr} \underline{-2}| & 3 & 5 & -20 \\ & & -6 & 2 \\ \hline & 3 & -1 & |\underline{-18} \end{array} $$
The result is 3x − 1. The remainder is −18.
Analysis Just as with long division, check the work by multiplying the quotient by the divisor and adding the remainder.
(x + 2)(3x − 1) − 18 = 3x2 + 5x − 20
Use synthetic division to divide 2x3 − x2 − 26x + 33 by x − 3.
Solution
The binomial divisor is x − 3, so k = 3. Add each column, multiply the result by 3, and repeat until the last column is reached.
$$ \begin{array}{rrrrr} \underline{3}| & 2 & -1 & -26 & 33 \\ & & 6 & 15 & -33 \\ \hline & 2 & 5 & -11 & |\underline{\phantom{00}0} \end{array} $$
The result is 2x2 + 5x − 11. The remainder is 0, so x − 3 is a factor of 2x3 − x2 − 26x + 33.
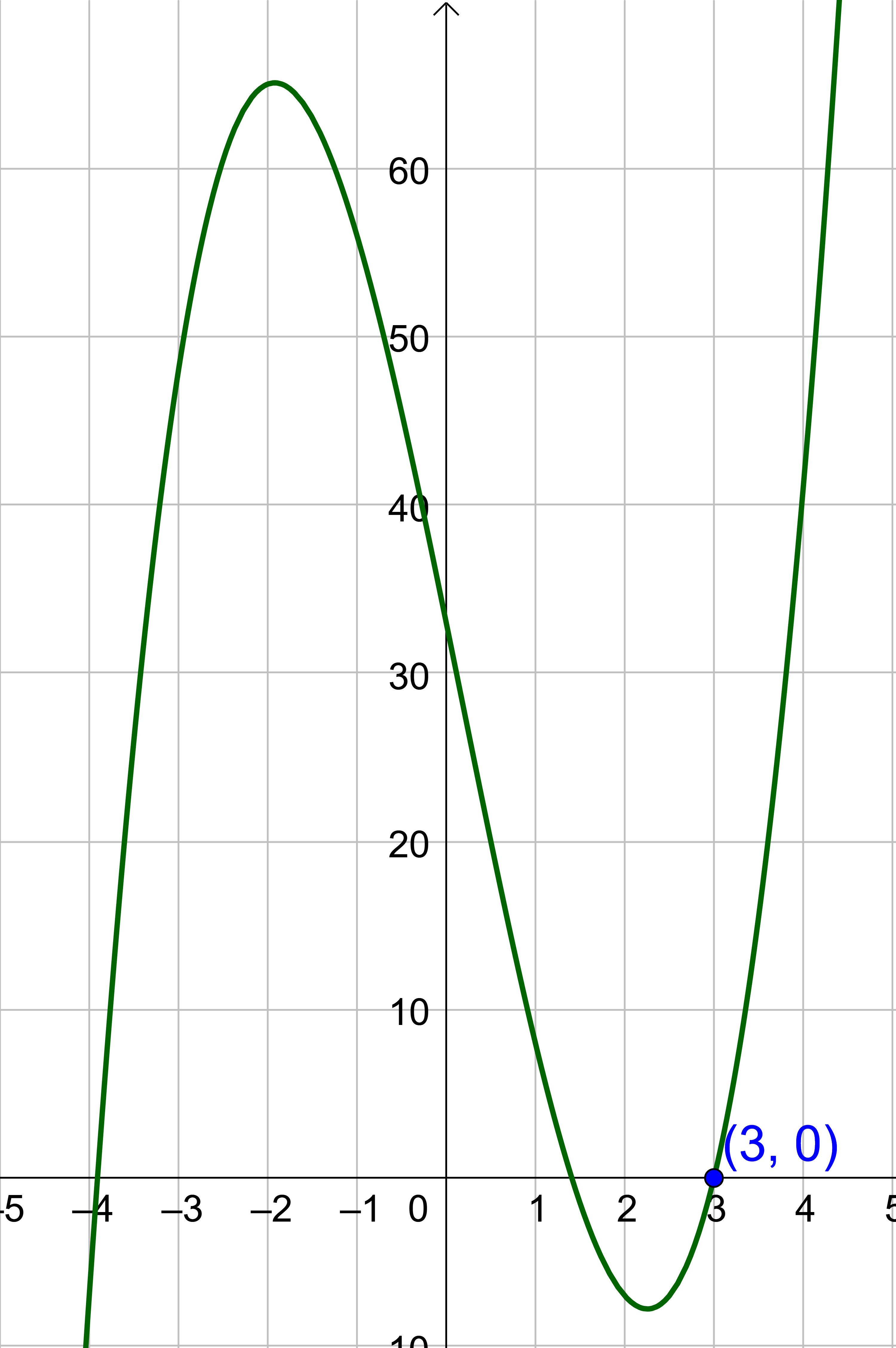
Analysis The graph of the polynomial function f(x) = 2x3 − x2 − 26x + 33 in figure 2 shows a zero at x = k = 3 because there is an x-intercept at x = 3. This confirms that x − 3 is a factor of 2x3 − x2 − 26x + 33.
Use synthetic division to divide 5x4 + 2x3 − 10x2 − 3 by x + 1.
Solution
Notice there is no x-term. Use a zero as the coefficient for that term. All powers of x and the constant must be represented in the coefficients for synthetic division.
The binomial divisor is x + 1 so k = −1. Add each column, multiply the result by −1, and repeat until the last column is reached.
$$ \begin{array}{rrrrr} \underline{−1}| & 5 & 2 & -10 & 0 & −3 \\ & & -5 & 3 & 7 & -7 \\ \hline & 5 & -3 & -7 & 7 & |\underline{-10} \end{array} $$
The remainder is −10, so the result is \(5x^3 - 3x^2 - 7x + 7 + \frac{-10}{x + 1}\).
Use synthetic division to divide x4 + 5x3 + 7x − 20 by x + 5.
Answer
\(x^3 + 7 + \frac{-55}{x + 5}\)
Polynomial division can be used to solve a variety of application problems involving expressions for area and volume. An example of this was at the beginning of this section.
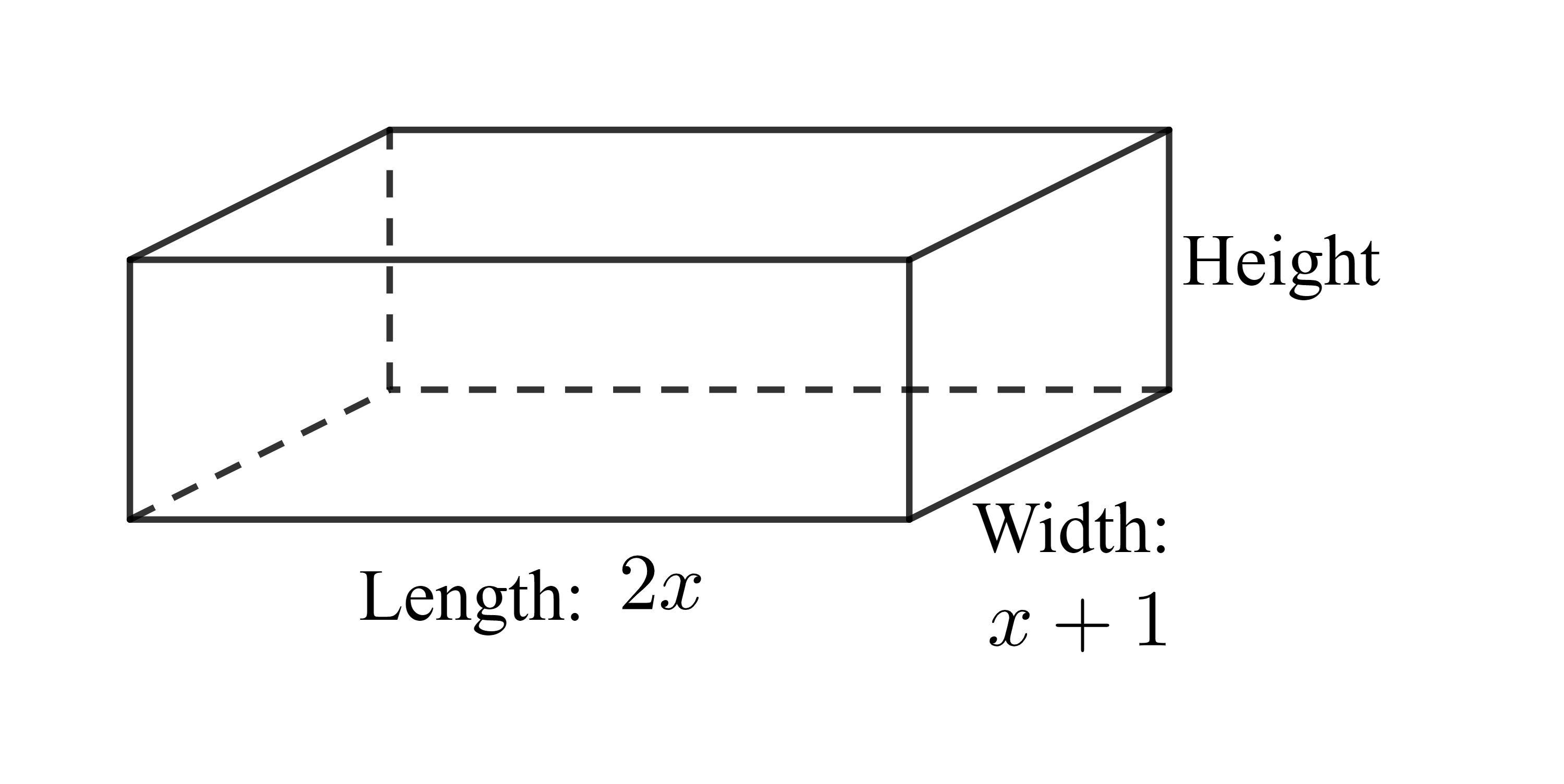
The volume of a rectangular solid is given by 2x3 − 4x2 − 6x. The length of the solid is 2x and the width is x + 1. Find the height of the solid.
Solution
There are a few ways to approach this problem. Divide the expression for the volume of the solid by the expressions for the length and width. A sketch is in figure 3.
Write an equation by substituting the known values into the formula for the volume of a rectangular solid.
V = l · w · h
2x3 − 4x2 − 6x = 2x · (x + 1) · h
To solve for h, first divide both sides by 2x.
$$ \frac{2x^3 - 4x^2 - 6x}{2x} = \frac{2x · (x + 1) · h}{2x} $$
x2 − 2x − 3 = (x + 1) · h
Now solve for h using synthetic division.
$$ h = \frac{x^2 - 2x - 3}{x + 1} $$
$$ \begin{array}{rrrr} \underline{−1}| & 1 & -2 & -3 \\ & & -1 & 3 \\ \hline & 1 & -3 & |\underline{\phantom{0}0} \end{array} $$
The quotient is x − 3 and the remainder is 0. The height of the solid is x − 3.
The area of a rectangle is 2x3 + 13x2 + 11x − 20. The width of the rectangle is x + 5. Find an expression for the length of the rectangle.
Answer
2x2 + 3x − 4
Given a polynomial dividend f(x) and a non-zero polynomial divisor d(x) where the degree of d(x) is less than or equal to the degree of f(x) there exist unique polynomials q(x) and r(x) such that
f(x) = d(x)·q(x) + r(x)
where q(x) is the quotient and r(x) is the remainder. The remainder is either equal to zero or has degree strictly less than d(x).
If r(x) = 0, then d(x) divides evenly into f(x). This means that both d(x) and q(x) are factors of f(x).
Synthetic division is a shortcut that can be used when the divisor is a binomial in the form x − k. In synthetic division, only the coefficients are used in the division process.
Helpful videos about this lesson.
