Precalculus by Richard Wright

Previous Lesson Table of Contents Next Lesson

Are you not my student and
has this helped you?

This book is available
to download as an epub.

Jesus said to her, “I am the resurrection and the life. The one who believes in me will live, even though they die; and whoever lives by believing in me will never die. Do you believe this?” John 11:25-26 NIV

4-01 Angle Measures

Mr. Wright teaches the lesson.

Summary: In this section, you will:

Draw angles in standard position.
Convert between degrees and radians.
Find coterminal angles.
Use applications of angles.

SDA NAD Content Standards (2018): PC.5.3

Using angles and their ideas can be used to find out how fast the tires on a race car are rotating if the car's speed is known. Before this can be calculated, basic concepts of angles and their units have to be learned. This topic is called trigonometry which means "measurement of triangles." However, it begins not with triangles, but with basic angles.

Angles

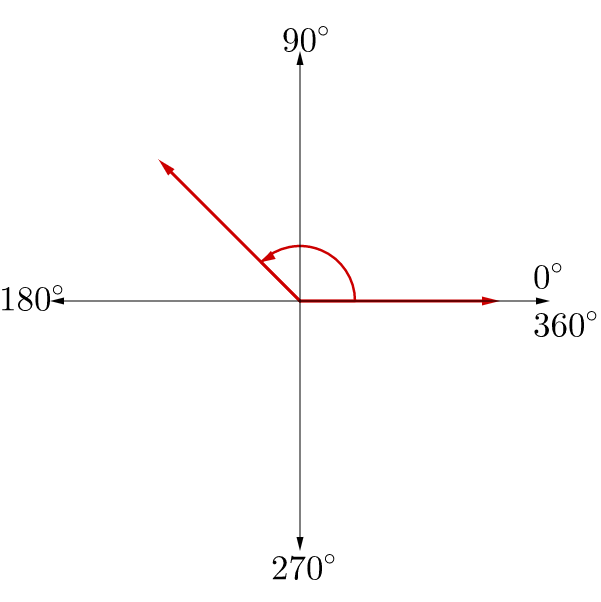
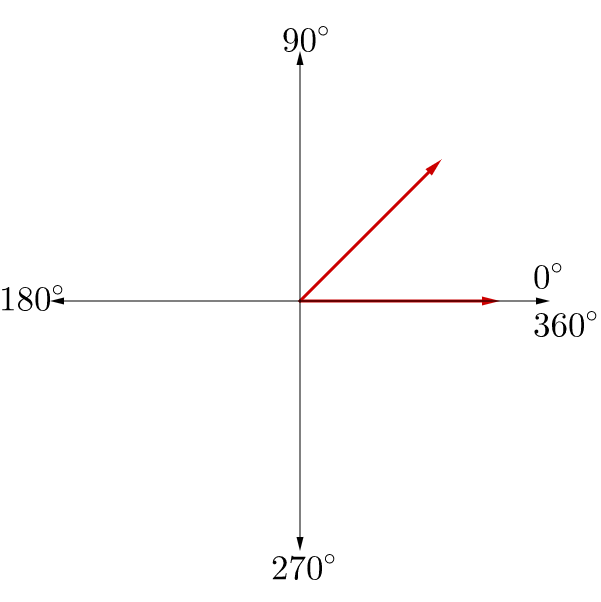
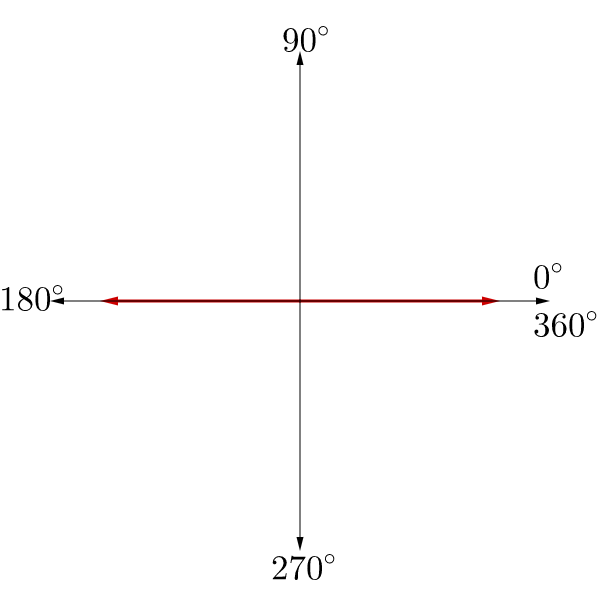
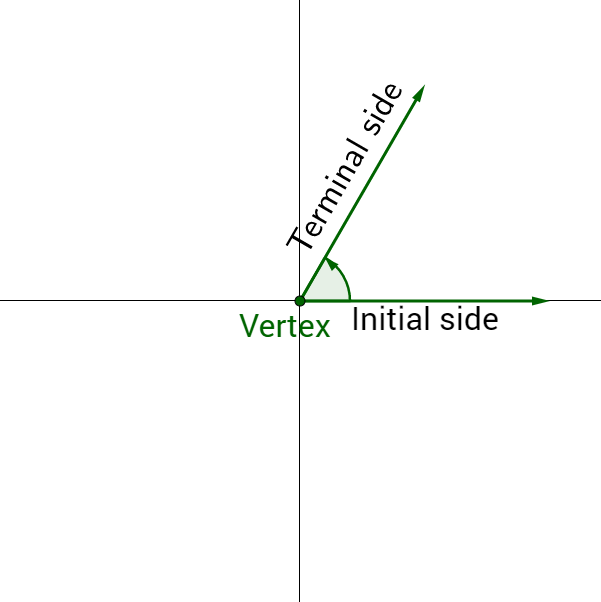
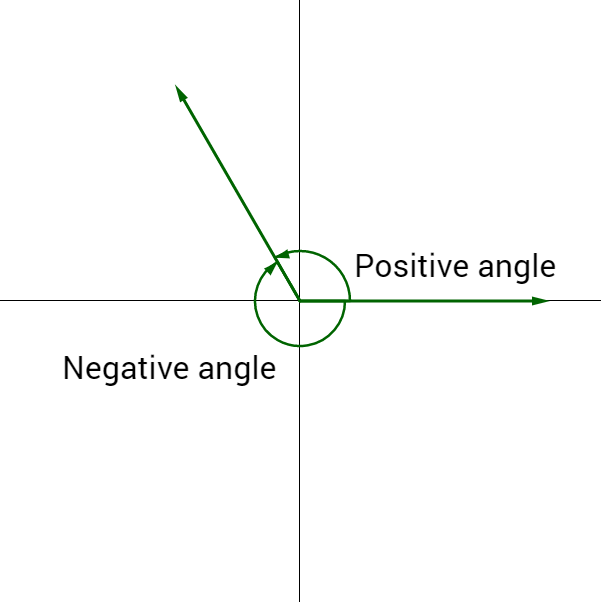
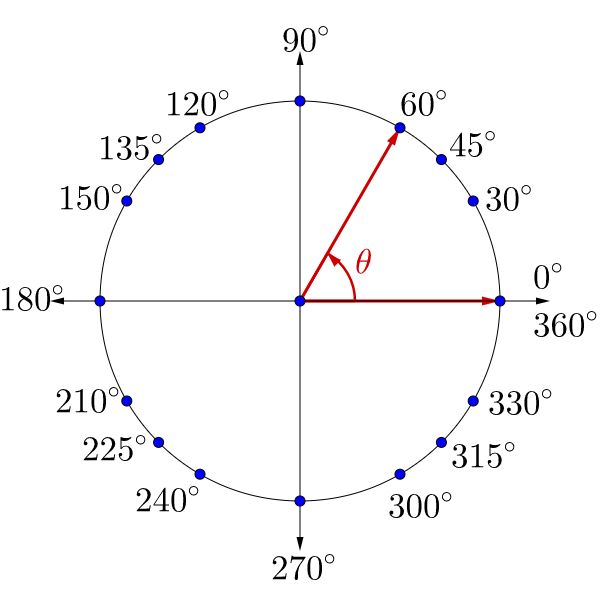
An angle is formed when two rays share a common end point called a vertex. A ray is a point on a line and all the points extending in one direction. An angle in standard position has the initial side on the positive x-axis. See figure 2a. The angle is measured in the counterclockwise direction. See figure 2b.

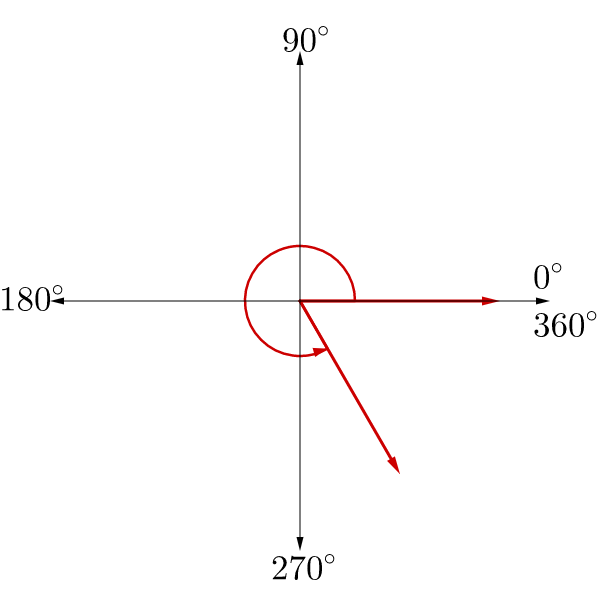
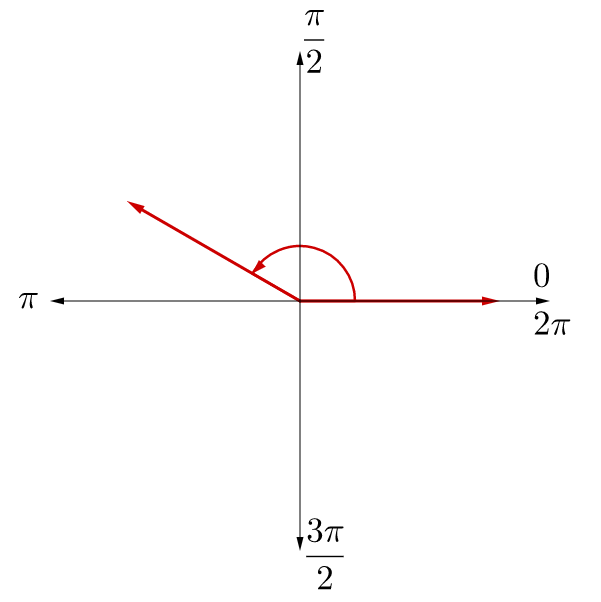
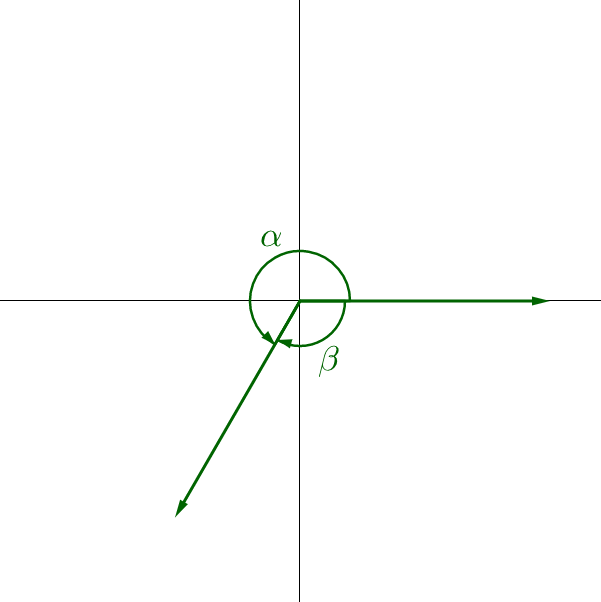
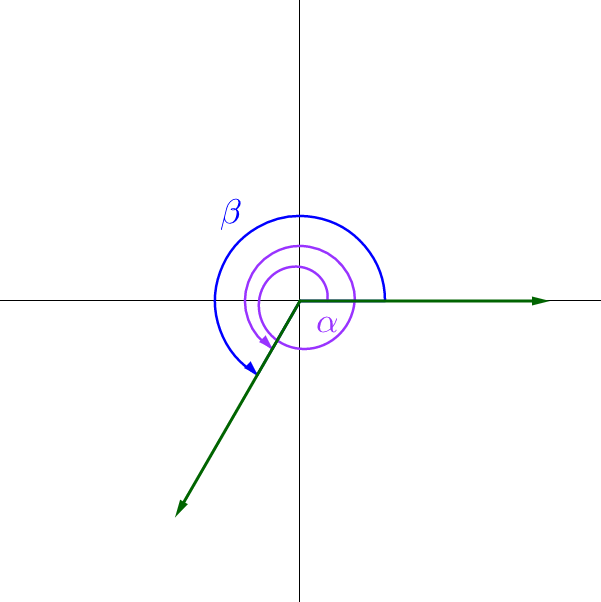
(a) Angle in standard position, (b) Positive and negative angle

Two angles in standard position can have initial and terminal sides in the same location as another angle but have a different measure. These are called coterminal angles. See figure 3. These are found by rotation the terminal side full circles in either direction.

Degree Measure

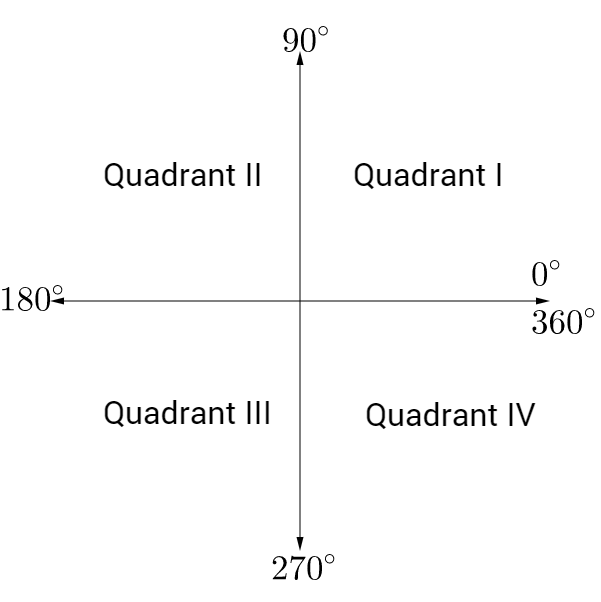
The most common unit for the measure of angles is degrees. There are 360° in a full revolution, 180° in a half revolution, and 90° in a quarter revolution. A coordinate plane is divided into four quadrants. Angles between 0° and 90° are in quadrant I, angles between 90° and 180° are in quadrant II, angles between 180° and 270° are in quadrant III, and angles between 270° and 360° are in quadrant IV.

To find coterminal angle measures, add or subtract multiples of 360°. This is because the terminal side rotates a complete revolution to return to the same location.

Find Coterminal Angles

Add or subtract 360° from the given angle measure. This can be repeated multiple times.

Find Coterminal Angles

Draw a 150° angle and then find a positive and negative coterminal angle.

Solution

To draw a 150° angle decide which quadrant it is in. Since 150° is between 90° and 180°, it is in quadrant II. 150° is closer to 180° than 90°, so draw it closer to the 180°.

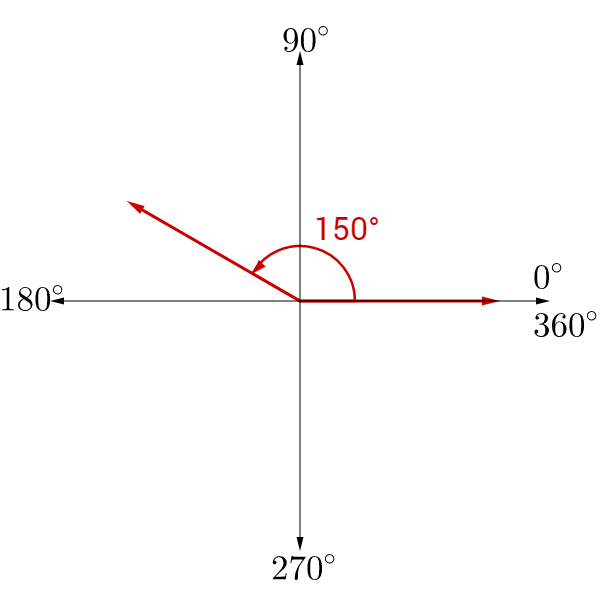
To find a positive coterminal angle try adding 360°.

150° + 360° = 510°

To find a negative coterminal angle try subtracting 360°.

150° − 360° = −210°

Find Coterminal Angles

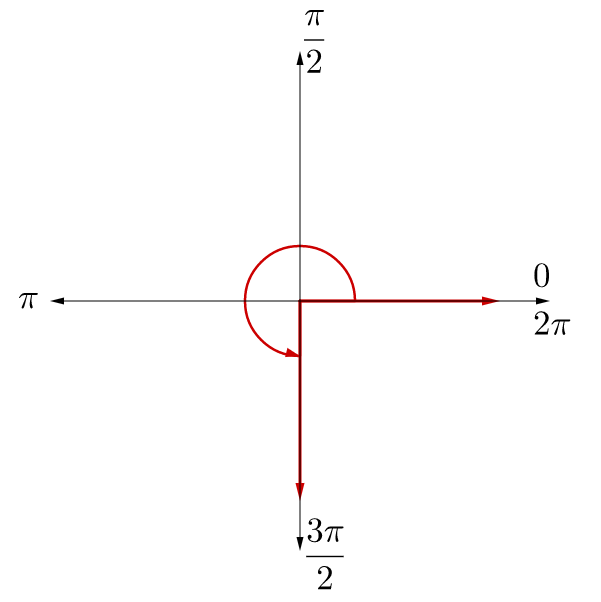
Draw a 560° angle and then find a positive and negative coterminal angle.

Solution

560° is not in the 0° to 360° range of our degree graph, so start by finding a coterminal angle between 0° and 360°. Since 560° is greater than 360°, subtract 360°.

560° − 360° = 200°

200° is between 180° and 270°, so it is in quadrant III close to the 180° mark.

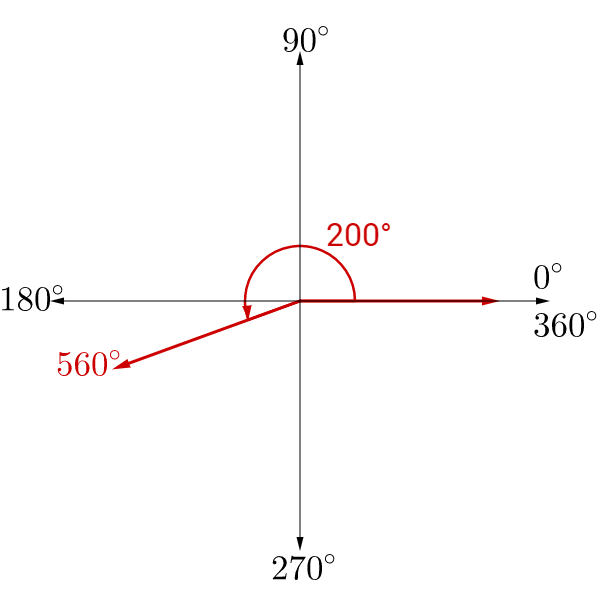
We already found that 200° is a positive coterminal angle. It is also correct to add 360° and say 920° is a positive coterminal angle.

To find a negative coterminal angle subtract 360° from the 200° coterminal angle we already found.

560° − 360° = 200°
200° − 360° = −160°

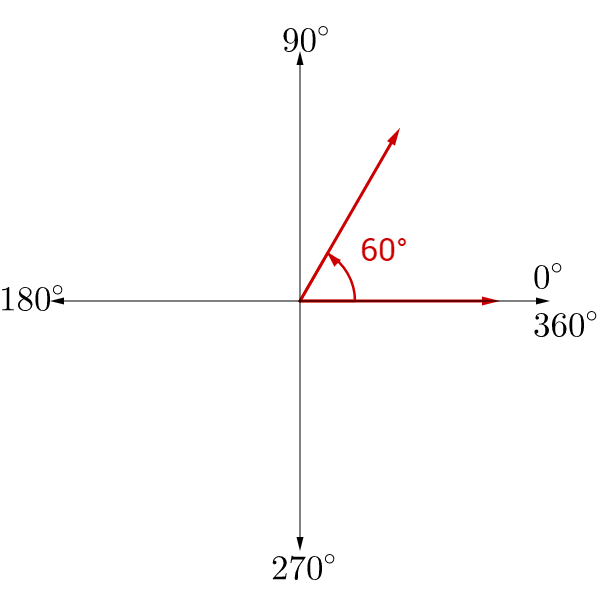
Draw a 60° angle and find a positive and negative coterminal angle.

Answer

; 420°; −300°

Complementary angles are two angles whose measures add to 90°. Supplementary angles are two angles whose measures add to 180°.

Find Complementary and Supplementary Angles

To find the complementary angle, subtract the given angle from 90°. If the given angle is greater than 90° there is no complement.

To find the supplementary angle, subtract the given angle from 180°. If the given angle is greater than 180° there is no supplement.

Find a Complement and Supplement

Find the a) complement and b) supplement of 60°.

Solution

To find the complement, subtract 60° from 90°.

90° − 60° = 30°
To find the supplement, subtract 60° from 180°.

180° − 60° = 120°

Find the a) complement and b) supplement of 115°.

Answer

no complement, 65°

Radian Measure

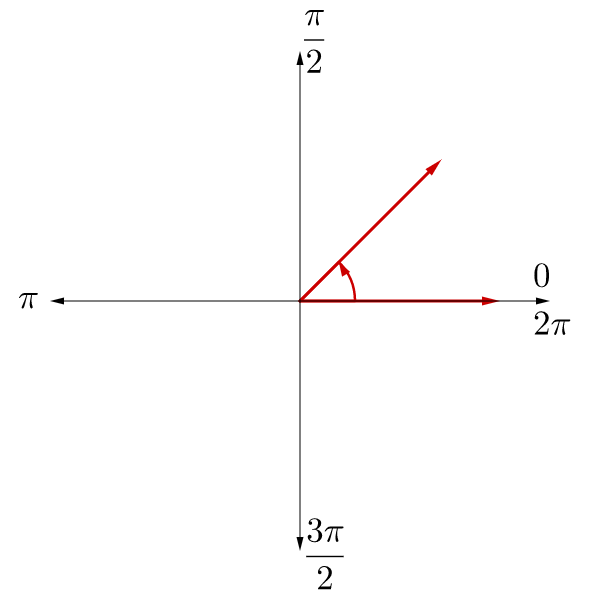
While degree measure is more common, it is not the most mathematically useful unit of angles. Radian measure is a unit which is often better in math. A radian is the angle where the arc length equals the radius. One revolution equals 2π radians; a half revolution is π radians; and a quarter revolution is $\frac{π}{2}$ radians. See the animation in figure 8a and the illustration in figure 9b.

One radian is the angle where the arc length equals the radius.

Radian and degree measures for some common angles.

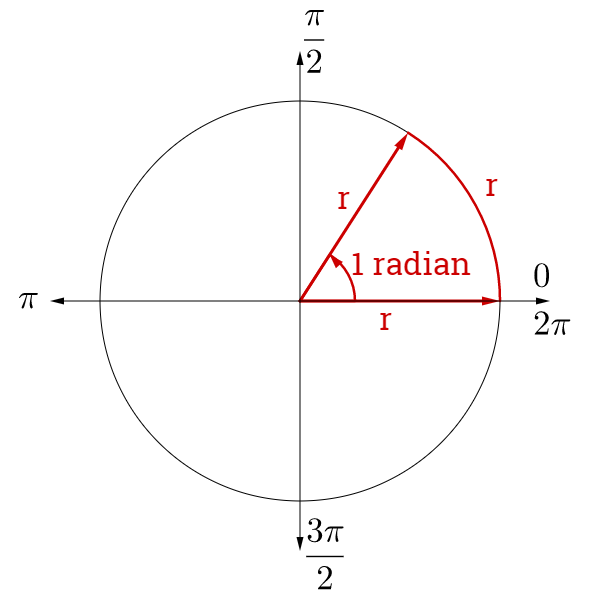
Notice angles in degrees have the degree symbol after them. Angles in radians have no written unit. If an angle measure is written without a unit, assume it is in radians.

Since degrees and radians are simply two different units for measuring angles, unit conversions can be performed using the conversion factor π radians = 180°. However, get used to working in radian measure, so do not convert all the radian measures to degrees simply to do calculations.

Convert From Degrees to Radians

Multiply the measure in degrees by $(\frac{π}{180 °})$ .

Convert From Radians to Degrees

Multiply the measure in radians by $(\frac{180 °}{π})$ .

Finding coterminal angles, complementary, and supplementary angles are the same as in degrees except use 2π instead of 360°, π instead of 180°, and $\frac{π}{2}$ instead of 90°.

Find Coterminal Angles in Radians

Add or subtract the given angle with 2π.

Find Complementary Angles in Radians

Subtract the given angle from $\frac{π}{2}$ . If the given angle is greater than $\frac{π}{2}$, there is no complement.

Find Supplementary Angles in Radians

Subtract the given angle from π. If the given angle is greater than π, there is no supplement.

Convert Angle Measures

Convert the degrees to radians or the radians to degrees.

120°
15°
$\frac{5 π}{4}$
$\frac{3 π}{10}$

Solution

Because this is converting degrees to radians, multiply the 120° by $(\frac{π}{180 °})$ .

$120 ° (\frac{π}{180 °}) = \frac{2 π}{3}$
Because this is converting degrees to radians, multiply the 15° by $(\frac{π}{180 °})$ .

$15 ° (\frac{π}{180 °}) = \frac{π}{12}$
Because this is converting degrees to radians, multiply the $\frac{5 π}{4}$ by $(\frac{180 °}{π})$ .

$(\frac{5 π}{4}) (\frac{180 °}{π}) = 225 °$
Because this is converting degrees to radians, multiply the $\frac{3 π}{10}$ by $(\frac{180 °}{π})$ .

$(\frac{3 π}{20}) (\frac{180 °}{π}) = 54 °$

a) Convert 100° to radians and b) $\frac{5 π}{8}$ to degrees.

Answer

$\frac{5 π}{9}$ ; 112.5°

Find Coterminal, Complementary, and Supplementary Angles

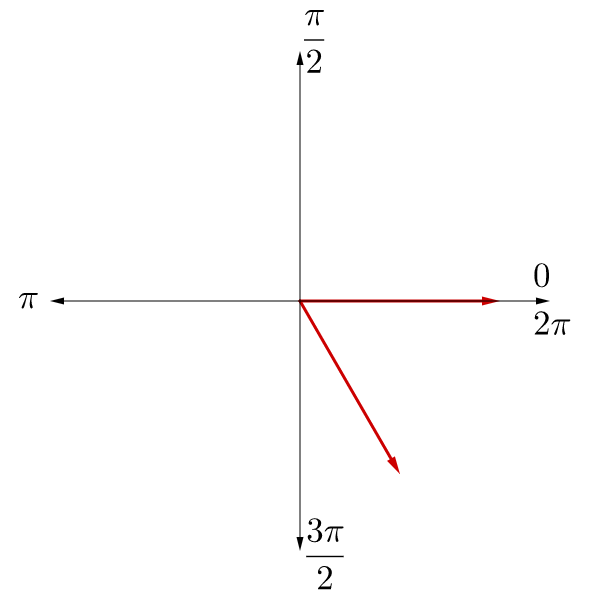
a) Draw the following angles, then find b) a positive and c) negative coterminal angle, d) the complementary angle, and e) the supplementary angle.

$\frac{π}{6}$
$\frac{3 π}{4}$

Solution

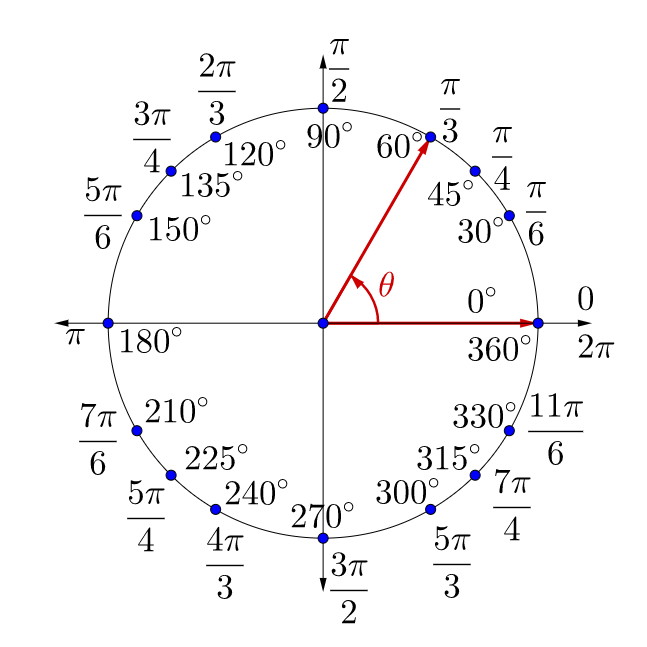
1. Compare $\frac{π}{6}$ to the graph in figure 9 to find where the angle is.
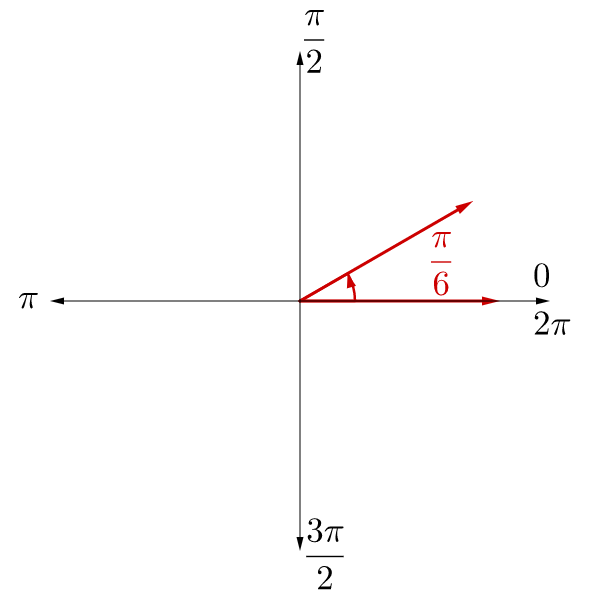
2. To find the positive coterminal angle, try adding 2π.
  
  $\begin{matrix} \frac{π}{6} + 2 π \\ \frac{π}{6} + \frac{12 π}{6} = \frac{13 π}{6} \end{matrix}$
3. To find a negative coterminal angle, try subtracting 2π.
  
  $\begin{matrix} \frac{π}{6} - 2 π \\ \frac{π}{6} - \frac{12 π}{6} = - \frac{11 π}{6} \end{matrix}$
4. To find the complementary angle, subtract the angle from $\frac{π}{2}$.
  
  $\begin{matrix} \frac{π}{2} - \frac{π}{6} \\ \frac{3 π}{6} - \frac{π}{6} = \frac{2 π}{6} = \frac{π}{3} \end{matrix}$
5. To find the supplementary angle, subtract the angle from π.
  
  $\begin{matrix} π - \frac{π}{6} \\ \frac{6 π}{6} - \frac{π}{6} = \frac{5 π}{6} \end{matrix}$
1. Compare $\frac{3 π}{4}$ to the graph in figure 9 so find where the angle is.
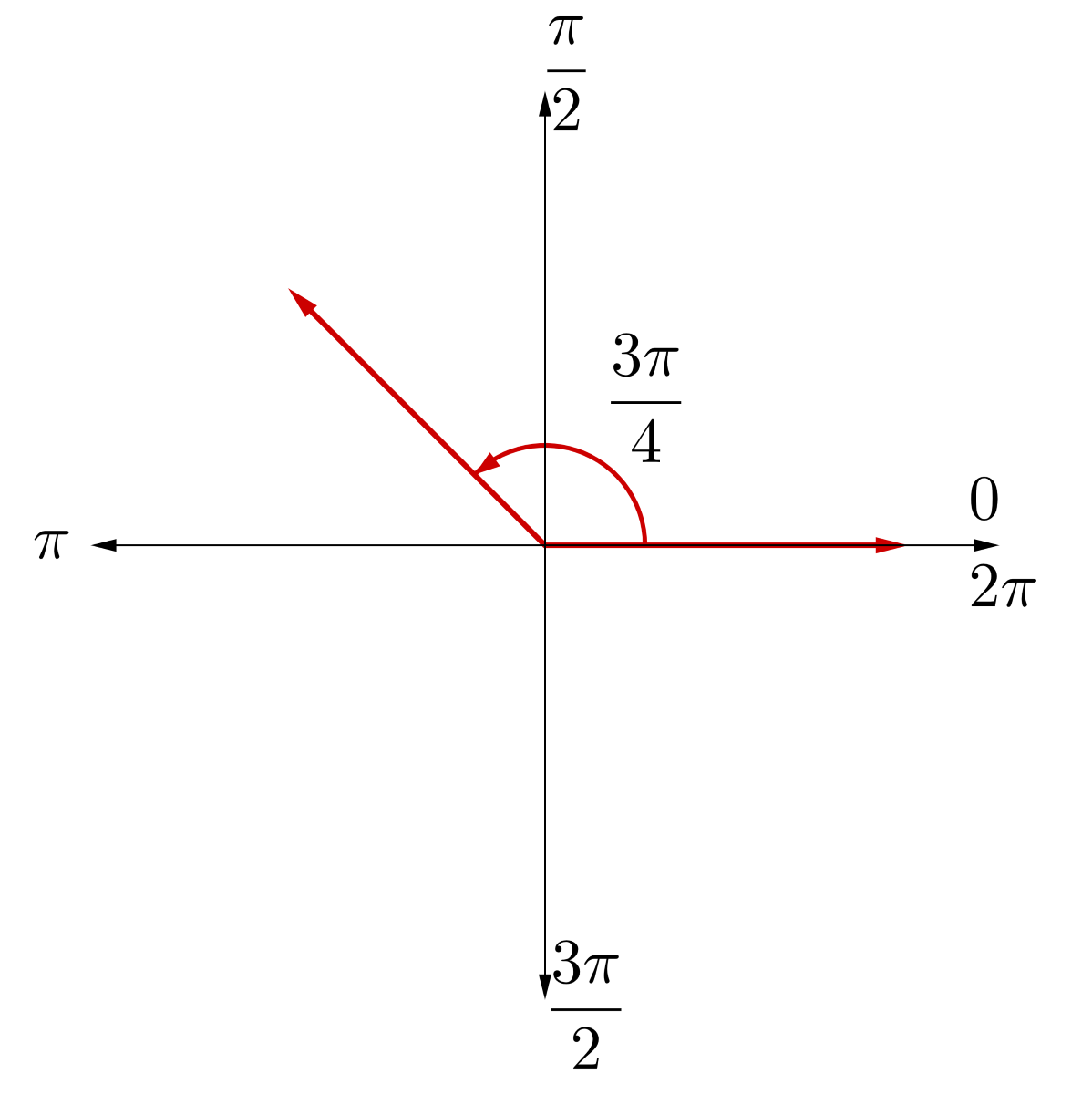
2. To find a positive coterminal angle, try adding 2π.
  
  $\begin{matrix} \frac{3 π}{4} + 2 π \\ \frac{3 π}{4} + \frac{8 π}{4} = \frac{11 π}{4} \end{matrix}$
3. To find a negative coterminal angle, try subtracting 2π.
  
  $\begin{matrix} \frac{3 π}{4} - 2 π \\ \frac{3 π}{4} - \frac{8 π}{4} = - \frac{5 π}{4} \end{matrix}$
4. Since $\frac{3 π}{4}$ is greater than $\frac{π}{2}$ there is no complement.
5. To find the supplementary angle, subtract the angle from π.
  
  $\begin{matrix} π - \frac{3 π}{4} \\ \frac{4 π}{4} - \frac{3 π}{4} = \frac{π}{4} \end{matrix}$

a) Draw the following angles, then find b) a positive and c) negative coterminal angle, d) the complementary angle, and e) the supplementary angle of $\frac{π}{12}$ .

Answers

$\frac{25 π}{12}$ ; $- \frac{23 π}{12}$ ; $\frac{5 π}{12}$ ; $\frac{11 π}{12}$

Applications

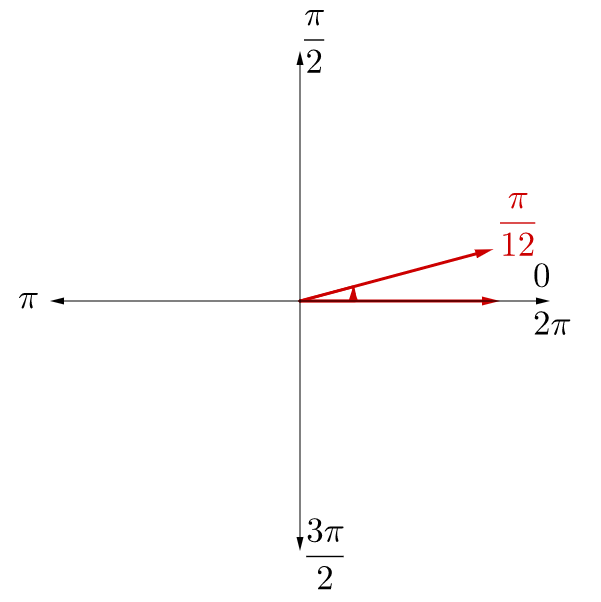
Because one radian is the angle where the arc length equals the radius, radians can be used to calculate the arc length of any angle. The arc length is a fraction of the circumference of the circle. If the angle, θ, is in radians, the fraction of the circle is $\frac{θ}{2 π}$ . Multiply that with the circumference of the circle to get the formula for arc length.

$s = 2 π r (\frac{θ}{2 π})$

s = rθ

Arc Length

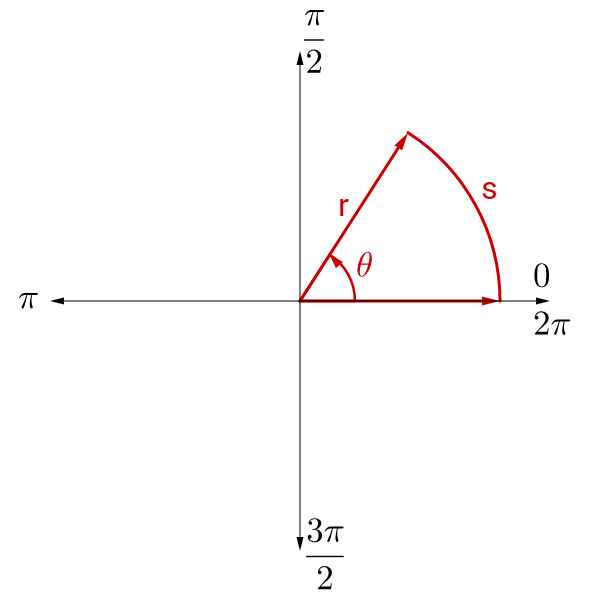
s = rθ

where s = arc length, r = radius, and θ = angle in radians.

The area of the sector formed by the angle and arc, is a fraction of a circle. Multiply the area of the circle by the fraction $\frac{θ}{2 π}$ .

$\begin{matrix} A = π r^{2} (\frac{θ}{2 π}) \\ A = \frac{1}{2} r^{2} θ \end{matrix}$

Area of a Sector

$A = \frac{1}{2} r^{2} θ$

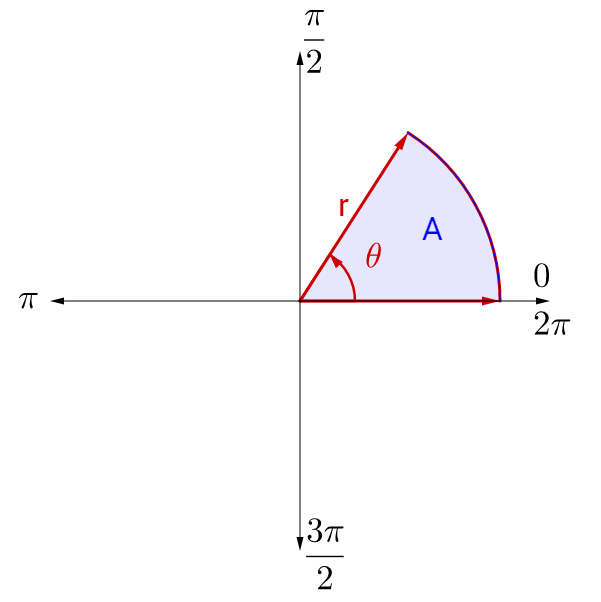
where A = area of the sector, r = radius, and θ = angle in radians.

The other application of angles for this lesson is the relationship between linear velocity and angular velocity. Linear velocity, v, is the rate that displacement changes. In the case of a rotating object, it is the speed at which a point on the object travels. Angular velocity, ω, is the rate that a rotating object's angle changes. By dividing both sides of the arc length formula by time, we can find the relationship between linear and angular velocity.

s = rθ

$\frac{s}{t} = r \frac{θ}{t}$

v = rω

Linear and Angular Velocity of Rotating Objects

Linear Velocity, v, is the rate the displacement a point on an object is changing.

$v = \frac{s}{t}$

Angular velocity, ω, is the rate the angle of a point on an object is changing.

$ω = \frac{θ}{t}$

The relationship between linear and angular velocity is

v = rω

Applications

In the great plains, fields are often laid out in circles or sectors of circles because of the way the irrigation systems work. The irrigation system is hooked to a well in the center of the field and then an arm hundreds of feet long rotates around the field. If one field is shaped like a sector with central angle of 120° and has a radius of 400 feet, a) how far does the end of the end of the irrigation system arm travel? b) What is the area of the field? c) If it takes 4 hours to water the whole field, what is the angular velocity of the irrigation system? d) What is the linear velocity of the end of the irrigation system?

Solution

This question is asking arc length. In order to use the arc length formula, the angle needs to be in radians.

$120 ° (\frac{π}{180 °}) = \frac{2 π}{3}$

Now use the arc length formula.

s = rθ

$s = (400 ft) (\frac{2 π}{3})$

$s = \frac{800 π}{3} ft \approx 838.76 ft$
To find the area, use the area formula, but remember to use radians, $\frac{2 π}{3}$ , instead of the degrees, 120°.

$A = \frac{1}{2} r^{2} θ$

$A = \frac{1}{2} {(400 ft)}^{2} (\frac{2 π}{3})$

$A = \frac{160,000 π}{3} {ft}^{2} \approx 167551.61 {ft}^{2}$
Angular velocity is the rate of change of angle. Use radians. For the time, minutes or seconds is more common for angular velocity than hours, let us use minutes. 4 hours = 240 minutes.

$ω = \frac{θ}{t}$

$ω = \frac{(\frac{2 π}{3})}{240 min} = \frac{π}{360} \frac{rad}{min} \approx 0.00873 \frac{rad}{min}$
Use the angular and linear velocity relationship to change the angular velocity to linear velocity.

$v = r ω$

$v = (400 ft) (\frac{π}{360} \frac{rad}{min})$

$v = \frac{10 π}{9} \frac{ft}{min} \approx 3.49 \frac{ft}{min}$

a) What is the angle through which the minute hand of a clock moves in a half hour in radians. b) What is the angular velocity of the minute hand if it is 6 inches long in rad/s? c) What is the linear velocity of the end of the minute hand in in./s?

Answer

π radians; $\frac{π}{30} \frac{rad}{s} \approx 0.105 \frac{rad}{s}$ ; $\frac{π}{5} \frac{in.}{s} \approx 0.628 \frac{in.}{s}$

Lesson Summary

Find Coterminal Angles

Add or subtract 360° from the given angle measure. This can be repeated multiple times.

Find Complementary and Supplementary Angles

To find the complementary angle, subtract the given angle from 90°. If the given angle is greater than 90° there is no complement.

To find the supplementary angle, subtract the given angle from 180°. If the given angle is greater than 180° there is no supplement.

Convert From Degrees to Radians

Multiply the measure in degrees by $(\frac{π}{180 °})$ .

Convert From Radians to Degrees

Multiply the measure in radians by $(\frac{180 °}{π})$ .

Find Coterminal Angles in Radians

Add or subtract the given angle with 2π.

Find Complementary Angles in Radians

Subtract the given angle from $\frac{π}{2}$ . If the given angle is greater than π⁄2, there is no complement.

Find Supplementary Angles in Radians

Subtract the given angle from π. If the given angle is greater than π, there is no supplement.

Arc Length

s = rθ

where s = arc length, r = radius, and θ = angle in radians.

Area of a Sector

$A = \frac{1}{2} r^{2} θ$

where A = area of the sector, r = radius, and θ = angle in radians.

Linear and Angular Velocity of Rotating Objects

Linear Velocity, v, is the rate the displacement a point on an object is changing.

$v = \frac{s}{t}$

Angular velocity, ω, is the rate the angle of a point on an object is changing.

$ω = \frac{θ}{t}$

The relationship between linear and angular velocity is

v = rω

Helpful videos about this lesson.

Mr. Wright Teaches the Lesson (https://youtu.be/exrb-FqbmRE)
Angles in Standard Position (http://openstaxcollege.org/l/standardpos)
Angle of Rotation (http://openstaxcollege.org/l/angleofrotation)
Coterminal Angles (http://openstaxcollege.org/l/coterminal)
Determining Coterminal Angles (http://openstaxcollege.org/l/detcoterm)
Positive and Negative Coterminal Angles (http://openstaxcollege.org/l/posnegcoterm)
Radian Measure (http://openstaxcollege.org/l/radianmeas)
Coterminal Angles in Radians (http://openstaxcollege.org/l/cotermrad)
Arc Length and Area of a Sector (http://openstaxcollege.org/l/arclength)

Practice Exercises

Draw an angle in standard position. Label the vertex, initial side, and terminal side.
For each given angle a) draw the angle in standard position, b) convert it to the other angle unit, c) find a positive coterminal angle, d) find a negative coterminal angle, e) find the complementary angle, and f) find the supplementary angle.
300°
135°
−120°
30°
405°
−540°
$\frac{π}{4}$
$\frac{5 π}{6}$
$\frac{3 π}{2}$
$- \frac{π}{3}$
$- \frac{11 π}{4}$
$\frac{10 π}{3}$
Problem Solving
A car with 16 inch diameter tires is traveling at 25 mi/hr. Find the angular speed of the tires in rad/min. How many revolutions per minute do the tires make?
An arc has a central angle of 30° and a radius of 128 ft. Find the (a) length of the arc and (b) the area of the sector.
Mixed Review
(3-05) A substance has a half-life of 3.1 seconds. If the initial amount of the substance was 100 grams, how many half-lives will have passed before the substance decays to 10 grams? What is the total time of decay?
(3-04) Solve 4 ⋅ 3^{x + 10} = 7
(3-03) Condense log₃ x − 2 log₃ y + 7 log₃ z
(2-06) Find all the zeros of f(x) = x³ − 4x² + 6x − 4
(1-07) Identify the parent function and describe the transformations: g(x) = −2(x + 3)² + 4

Answers

; $\frac{5 π}{3}$ ; 660°; −60°; none; none
; $\frac{3 π}{4}$ ; 495°; −225°; none; 45°
; $- \frac{2 π}{3}$ ; 240°; −480°; none; none
; $\frac{π}{6}$ ; 390°; −330°; 60°; 150°
; $\frac{9 π}{4}$ ; 45°; −315°; none; none
; −3π 180°; −180°; none; none
; 45°; $\frac{9 π}{4}$ ; − $\frac{7 π}{4}$ ; $\frac{π}{4}$ ; $\frac{3 π}{4}$
; 150°; $\frac{17 π}{6}$ ; − $\frac{7 π}{6}$ ; none; $\frac{π}{6}$
; 270°; $\frac{7 π}{2}$ ; − $\frac{π}{2}$ ; none; none
; −60°; $\frac{5 π}{3}$ ; − $\frac{7 π}{3}$ ; none; none
; −495°; − $\frac{3 π}{4}$ ; $\frac{5 π}{4}$ ; none; none
; 600°; $\frac{4 π}{3}$ ; − $\frac{2 π}{3}$ ; none; none
3300 rad/min; 525.2 rev/min
$\frac{64π}{3}$ ft.; 4289.3 ft²
3.32 half-lives; 10.298 s
−9.491
${log}_{3} \frac{x z^{7}}{y^{2}}$
2, 1 + i, 1 − i
quadratic function; reflected over the x-axis, vertical stretch by factor of 2, translated left 3 and up 4