Precalculus by Richard Wright

Previous Lesson Table of Contents Next Lesson

Are you not my student and
has this helped you?

This book is available
to download as an epub.

Have I not commanded you? Be strong and courageous. Do not be afraid; do not be discouraged, for the Lord your God will be with you wherever you go. Joshua 1:9 NIV

4-02 Unit Circle

Mr. Wright teaches the lesson.

Summary: In this section, you will:

Understand the unit circle.
Use the unit circle to evaluate trigonometric functions.
Use even and odd trigonometric functions.
Use a calculator to evaluate trigonometric functions.

SDA NAD Content Standards (2018): PC.5.3

A carousel takes a child for a ride on a colorful animal in a circle. Using trigonometric functions and the unit circle, we can calculate the location of the rider at any given time.

Unit Circle

Think of a circle centered at the origin with a radius of one. Since the radius is one, it is called a unit circle. A similar circle was used to show angle measures. Now coordinates are added to the circle.

Unit Circle

The Unit Circle is a circle centered at the origin with radius equal to 1. It can be used to evaluate trigonometric functions.

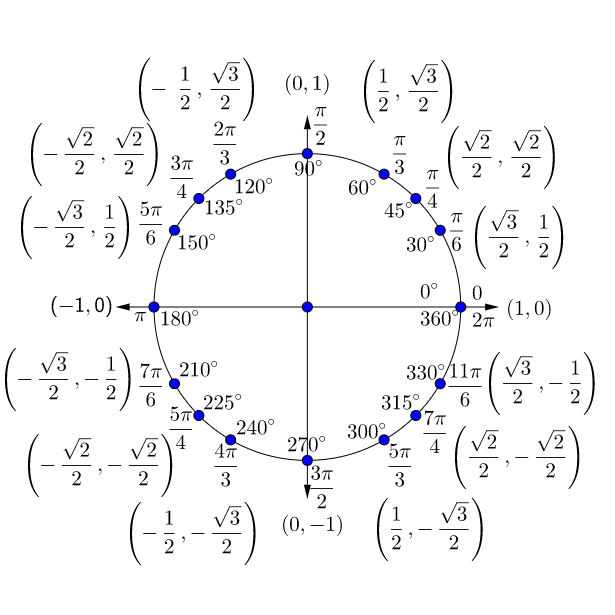
Think of a number line wrapped around the circle. This would measure the arc length. Remember arc length is s = rθ and since r = 1, then s = θ. The x and y-coordinates then would be functions of the arc length which equals the angle in radians. These functions are called trigonometric functions.

Trigonometric Functions: Unit Circle

Name	Formula	Name	Formula
Sine	sin θ = y	Cosecant	csc θ = $\frac{1}{y}$
Cosine	cos θ = x	Secant	sec θ = $\frac{1}{x}$
Tangent	tan θ = $\frac{y}{x}$	Cotangent	cot θ = $\frac{x}{y}$

Note: These are undefined when the denominator of the fraction equals 0.

Evaluate Trigonometric Functions

Evaluate the six trigonometric functions for the given angles.

θ = π
$θ = \frac{π}{4}$
$θ = \frac{4 π}{3}$
$θ = \frac{11 π}{6}$

Solution

Use the angle on the unit circle to find the corresponding x and y-coordinates. For π, x = −1 and y = 0.

$sin π = y = 0$	$csc π = \frac{1}{y} = \frac{1}{0} = undefined$
$cos π = x = - 1$	$sec π = \frac{1}{x} = \frac{1}{- 1} = - 1$
$tan π = \frac{y}{x} = \frac{0}{- 1} = 0$	$cot π = \frac{x}{y} = \frac{- 1}{0} = undefined$

Use the angle on the unit circle to find the corresponding x and y-coordinates. For $\frac{π}{4}$ , x = $\frac{\sqrt{2}}{2}$ and y = $\frac{\sqrt{2}}{2}$ .

$sin \frac{π}{4} = y = \frac{\sqrt{2}}{2}$	$csc \frac{π}{4} = \frac{1}{y} = \frac{1}{\frac{\sqrt{2}}{2}} = \sqrt{2}$
$cos \frac{π}{4} = x = \frac{\sqrt{2}}{2}$	$sec \frac{π}{4} = \frac{1}{x} = \frac{1}{\frac{\sqrt{2}}{2}} = \sqrt{2}$
$tan \frac{π}{4} = \frac{y}{x} = \frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = 1$	$cot \frac{π}{4} = \frac{x}{y} = \frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = 1$

Use the angle on the unit circle to find the corresponding x and y-coordinates. For $\frac{4 π}{3}$ , x = $- \frac{1}{2}$ and y = $- \frac{\sqrt{3}}{2}$ .

$sin \frac{4 π}{3} = y = - \frac{\sqrt{3}}{2}$	$csc \frac{4 π}{3} = \frac{1}{y} = \frac{1}{- \frac{\sqrt{3}}{2}} = - \frac{2 \sqrt{3}}{3}$
$cos \frac{4 π}{3} = x = - \frac{1}{2}$	$sec \frac{4 π}{3} = \frac{1}{x} = \frac{1}{- \frac{1}{2}} = - 2$
$tan \frac{4 π}{3} = \frac{y}{x} = \frac{- \frac{\sqrt{3}}{2}}{- \frac{1}{2}} = \sqrt{3}$	$cot \frac{4 π}{3} = \frac{x}{y} = \frac{- \frac{1}{2}}{- \frac{\sqrt{3}}{2}} = \frac{\sqrt{3}}{3}$

Use the angle on the unit circle to find the corresponding x and y-coordinates. For $\frac{11 π}{6}$ , x = $\frac{\sqrt{3}}{2}$ and y = $- \frac{1}{2}$ .

$sin \frac{11 π}{6} = y = - \frac{1}{2}$	$csc \frac{11 π}{6} = \frac{1}{y} = \frac{1}{- \frac{1}{2}} = - 2$
$cos \frac{11 π}{6} = x = \frac{\sqrt{3}}{2}$	$sec \frac{11 π}{6} = \frac{1}{x} = \frac{1}{\frac{\sqrt{3}}{2}} = \frac{2 \sqrt{3}}{3}$
$tan \frac{11 π}{6} = \frac{y}{x} = \frac{- \frac{1}{2}}{\frac{\sqrt{3}}{2}} = - \frac{\sqrt{3}}{3}$	$cot \frac{11 π}{6} = \frac{x}{y} = \frac{\frac{\sqrt{3}}{2}}{- \frac{1}{2}} = - \sqrt{3}$

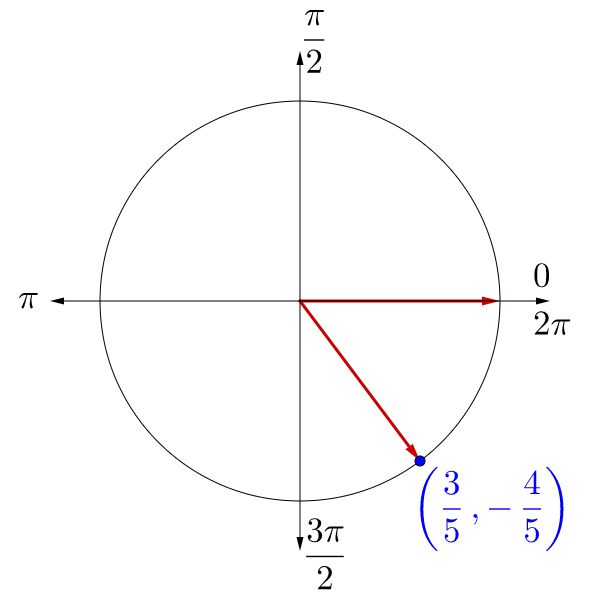
Evaluate the six trigonometric functions for $θ = \frac{π}{2}$ .

Answers

$sin \frac{π}{2} = 1$ ; $cos \frac{π}{2} = 0$ ; $tan \frac{π}{2} = undefined$ ; $csc \frac{π}{2} = 1$ ; $sec \frac{π}{2} = undefined$ ; $cot \frac{π}{2} = 0$

Evaluate Trigonometric Functions Not Between 0 and 2π

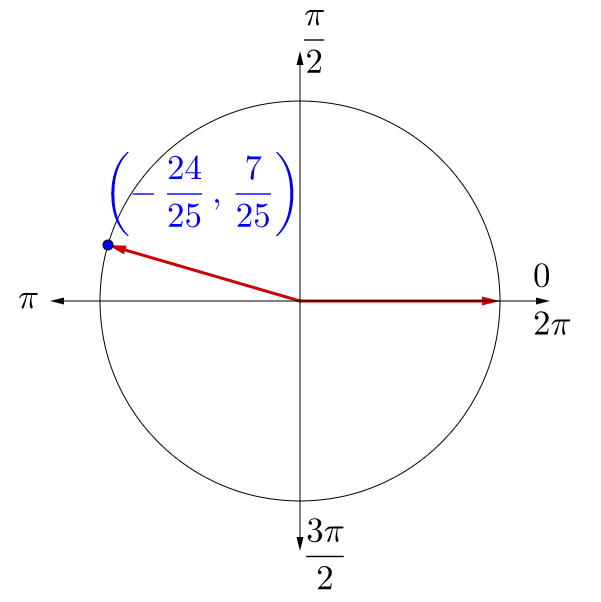
Evaluate the six trigonometric functions for the given angles.

a. $θ = - \frac{π}{3}$ , b. $θ = \frac{9 π}{4}$

Solution

$θ = - \frac{π}{3}$ is not on the unit circle because it is negative. The first step is to find a coterminal angle between 0 and 2π.

$\begin{array}{l} θ = - \frac{π}{3} + 2 π \\ θ = - \frac{π}{3} + \frac{6 π}{3} \\ θ = \frac{5 π}{3} \end{array}$

The coordinates for $θ = \frac{5 π}{3}$ are $(\frac{1}{2}, - \frac{\sqrt{3}}{2})$ . Use those in the trigonometric functions and evaluate.

$sin (- \frac{π}{3}) = y = - \frac{\sqrt{3}}{2}$	$csc (- \frac{π}{3}) = \frac{1}{y} = \frac{1}{- \frac{\sqrt{3}}{2}} = - \frac{2 \sqrt{3}}{3}$
$cos (- \frac{π}{3}) = x = \frac{1}{2}$	$sec (- \frac{π}{3}) = \frac{1}{x} = \frac{1}{\frac{1}{2}} = 2$
$tan (- \frac{π}{3}) = \frac{y}{x} = \frac{- \frac{\sqrt{3}}{2}}{\frac{1}{2}} = - \sqrt{3}$	$cot (- \frac{π}{3}) = \frac{x}{y} = \frac{\frac{1}{2}}{- \frac{\sqrt{3}}{2}} = - \frac{\sqrt{3}}{3}$

$θ = \frac{9 π}{4}$ is not on the unit circle because it is greater than 2π. The first step is to find a coterminal angle between 0 and 2π.

$\begin{array}{l} θ = \frac{9 π}{4} - 2 π \\ θ = \frac{9 π}{4} - \frac{8 π}{4} \\ θ = \frac{π}{4} \end{array}$

The coordinates for $θ = \frac{π}{4}$ are $(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2})$ . Use those in the trigonometric functions and evaluate.

$sin \frac{9 π}{4} = y = \frac{\sqrt{2}}{2}$	$csc \frac{9 π}{4} = \frac{1}{y} = \frac{1}{\frac{\sqrt{2}}{2}} = \sqrt{2}$
$cos \frac{9 π}{4} = x = \frac{\sqrt{2}}{2}$	$sec \frac{9 π}{4} = \frac{1}{x} = \frac{1}{\frac{\sqrt{2}}{2}} = \sqrt{2}$
$tan \frac{9 π}{4} = \frac{y}{x} = \frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = 1$	$cot \frac{9 π}{4} = \frac{x}{y} = \frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = 1$

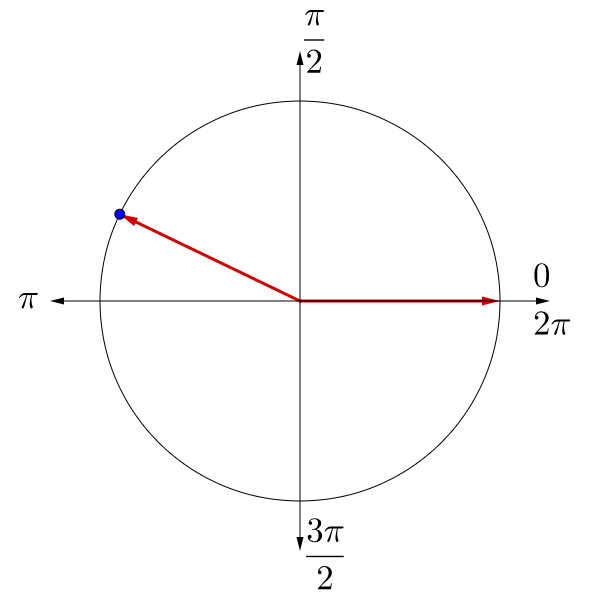
Evaluate the six trigonometric functions for $θ = 3 π$ .

Answers

$sin 3 π = 0$ ; $cos 3 π = - 1$ ; $tan 3 π = 0$ ; $csc 3 π = undefined$ ; $sec 3 π = - 1$ ; $cot 3 π = undefined$

Even and Odd Trigonometric Identities

Notice the coordinates on the unit circle form a pattern. Moving up or down from the x-axis, the coordinates are the same, only with different signs. This indicates symmetry.

Functions symmetric over the y-axis are classified as even. Functions symmetric about the origin are classified as odd. The following formulas are called identities because both sides are equal for all values of the variable.

Even and Odd Trigonometric Identities

Even functions are cosine and secant.

cos(−u) = cos(u)

sec(−u) = sec(u)

Odd functions are sine, cosecant, tangent, and cotangent.

sin(−u) = −sin(u)	csc(−u) = −csc(u)
tan(−u) = −tan(u)	cot(−u) = −cot(u)

Even and Odd Trigonometric Functions

If sin(x) = 1, what is sin(−x)?

Solution

Sine is an odd trigonometric function, so use the identity to solve the problem.

sin(−x) = −sin(x)
sin(−x) = −1

If sec(x) = 2, what is −sec(x)?

Answer

Use a Calculator

Calculators have two or three units for angles. These only matter when using the trigonometric functions. Make sure your calculator is using the correct angle unit for each problem. The settings are in z, Settings, or SETUP.

Using a Calculator to Evaluate Trigonometric Functions

Use a calculator to evaluate

$sin \frac{π}{10}$
$tan \frac{2 π}{3}$
$sec 120 °$

Solution

The angle $\frac{π}{10}$ is in radians. Make sure the calculator is in radian mode. Then use the calculator.

On a TI-84 calculator.

˜ y B ¥ À Ê ~ ¤ Í
sin(π/10) = 0.3090

On a NumWorks calculator.

s n / 1 0 R ) X
$\sin\left(\frac{π}{10}\right) = 0.3090$
The angle $\frac{2 π}{3}$ is in radians. Make sure the calculator is in radian mode. Then use the calculator.

On a TI-84 calculator.

š Á y B ¥ Â ~ ¤ Í
tan(2π/3) = −1.7321

On a NumWorks calculator.

t 2 n / 3 R ) X
$\tan\left(\frac{2π}{3}\right) = −1.7321$
The angle 120° is in radians. Make sure the calculator is in degree mode. There is no SEC button on most calculators, but secant is the reciprocal of cosine as seen in their formulas.

$\begin{array}{l} sec θ = \frac{1}{x} & cos θ = x \\ Substitute & sec θ = \frac{1}{cos θ} \end{array}$

Then use the calculator.

On a TI-84 calculator.

À ¥ ™ À Á Ê ¤ Í
1/cos(120) = −2

On a NumWorks calculator.

1 / c 1 2 0 ) X
$\frac{1}{\cos(120)} = -2$

Evaluate a. tan 68° and b. $cot \frac{3 π}{11}$ using a calculator.

Answer

2.4751, 0.8665

Lesson Summary

Unit Circle

The Unit Circle is a circle centered at the origin with radius equal to 1. It can be used to evaluate trigonometric functions.

Trigonometric Functions: Unit Circle

Name	Formula	Name	Formula
Sine	sin θ = y	Cosecant	csc θ = $\frac{1}{y}$
Cosine	cos θ = x	Secant	sec θ = $\frac{1}{x}$
Tangent	tan θ = $\frac{y}{x}$	Cotangent	cot θ = $\frac{x}{y}$

Note: These are undefined when the denominator of the fraction equals 0.

Even and Odd Trigonometric Identities

Even functions are cosine and secant.

cos(−u) = cos(u)

sec(−u) = sec(u)

Odd functions are sine, cosecant, tangent, and cotangent.

sin(−u) = −sin(u)	csc(−u) = −csc(u)
tan(−u) = −tan(u)	cot(−u) = −cot(u)

Helpful videos about this lesson.

Mr. Wright Teaches the Lesson (https://youtu.be/nxh9wfMrpDc)
Trigonometric Functions Using the Unit Circle (http://openstaxcollege.org/l/trigunitcir)
Sine and Cosine from the Unit Circle (http://openstaxcollege.org/l/sincosuc)
Sine and Cosine from the Unit Circle and Multiples of Pi Divided by Six (http://openstaxcollege.org/l/sincosmult)
Sine and Cosine from the Unit Circle and Multiples of Pi Divided by Four (http://openstaxcollege.org/l/sincosmult4)
Determining Trig Function Values (http://openstaxcollege.org/l/trigfuncval)
More Examples of Determining Trig Functions (http://openstaxcollege.org/l/moretrigfun)
Trig Functions on a Calculator (http://openstaxcollege.org/l/trigcalc)

Practice Exercises

Draw and label the complete unit circle.
Evaluate the six trigonometric functions using the point on the unit circle.
Evaluate all six trigonometric functions for the given angle using the unit circle.
150°
$\frac{7 π}{6}$
0
$- \frac{3 π}{2}$
480°
$- \frac{11 π}{4}$
If tan(x) = 1.5, what is tan(−x)?
If −sec(x) = 2, what is sec(−x)?
Use a calculator to evaluate the expression
$cos \frac{5 π}{12}$
sin 100°
$csc \frac{π}{5}$
Problem Solving
If a child riding a pink horse starts a ride on a carousel at the point (1, 0) and it rotates in a circle around the origin, what is the coordinates of the child after 45 seconds given the carousel rotates at 1 revolution per minute?
Mixed Review
(4-01) a) draw the angle in standard position, b) convert it to the other angle unit, c) find a positive coterminal angle and d) find a negative coterminal angle of $\frac{6 π}{7}$ .
(4-01) A race car with an 18-inch diameter wheel is traveling at 180 mi/h. Find the angular speed of the wheels in rad/min. How many revolutions per minute do the wheels make?
(3-02) Evaluate without using a calculator: log₃ 81.
(3-04) Solve 2 log₃ (x − 1) = 10.
(2-08) Identify the asymptotes and graph $f (x) = \frac{2 x - 1}{x^{2}}$ .

Answers

$sin θ = - \frac{4}{5}$ $csc θ = - \frac{5}{4}$

$cos θ = \frac{3}{5}$ $sec θ = \frac{5}{3}$

$tan θ = - \frac{4}{3}$ $cot θ = - \frac{3}{4}$
$sin θ = \frac{7}{25}$ $csc θ = \frac{25}{7}$

$cos θ = - \frac{24}{25}$ $sec θ = - \frac{25}{24}$

$tan θ = - \frac{7}{24}$ $cot θ = - \frac{24}{7}$
$sin θ = \frac{1}{2}$ $csc θ = 2$

$cos θ = - \frac{\sqrt{3}}{2}$ $sec θ = - \frac{2 \sqrt{3}}{3}$

$tan θ = - \frac{\sqrt{3}}{3}$ $cot θ = - \sqrt{3}$
$sin θ = - \frac{1}{2}$ $csc θ = - 2$

$cos θ = - \frac{\sqrt{3}}{2}$ $sec θ = - \frac{2 \sqrt{3}}{3}$

$tan θ = \frac{\sqrt{3}}{3}$ $cot θ = \sqrt{3}$
$sin θ = 0$ $csc θ = undefined$

$cos θ = 1$ $sec θ = 1$

$tan θ = 0$ $cot θ = undefined$
$sin θ = 1$ $csc θ = 1$

$cos θ = 0$ $sec θ = undefined$

$tan θ = undefined$ $cot θ = 0$
$sin θ = \frac{\sqrt{3}}{2}$ $csc θ = \frac{2 \sqrt{3}}{3}$

$cos θ = - \frac{1}{2}$ $sec θ = - 2$

$tan θ = - \sqrt{3}$ $cot θ = - \frac{\sqrt{3}}{3}$
$sin θ = - \frac{\sqrt{2}}{2}$ $csc θ = - \sqrt{2}$

$cos θ = - \frac{\sqrt{2}}{2}$ $sec θ = - \sqrt{2}$

$tan θ = 1$ $cot θ = 1$
−1.5
−2
0.2588
0.9848
1.7013
(0, −1)
; $(\frac{1080}{7}) °$ ; $\frac{20 π}{7}$ ; $- \frac{8 π}{7}$
21120 rad/min; 3361 rev/min
4
244
VA: x = 0; HA: y = 0;

$sin θ = - \frac{4}{5}$	$csc θ = - \frac{5}{4}$
$cos θ = \frac{3}{5}$	$sec θ = \frac{5}{3}$
$tan θ = - \frac{4}{3}$	$cot θ = - \frac{3}{4}$

$sin θ = \frac{7}{25}$	$csc θ = \frac{25}{7}$
$cos θ = - \frac{24}{25}$	$sec θ = - \frac{25}{24}$
$tan θ = - \frac{7}{24}$	$cot θ = - \frac{24}{7}$

$sin θ = \frac{1}{2}$	$csc θ = 2$
$cos θ = - \frac{\sqrt{3}}{2}$	$sec θ = - \frac{2 \sqrt{3}}{3}$
$tan θ = - \frac{\sqrt{3}}{3}$	$cot θ = - \sqrt{3}$

$sin θ = - \frac{1}{2}$	$csc θ = - 2$
$cos θ = - \frac{\sqrt{3}}{2}$	$sec θ = - \frac{2 \sqrt{3}}{3}$
$tan θ = \frac{\sqrt{3}}{3}$	$cot θ = \sqrt{3}$

$sin θ = 0$	$csc θ = undefined$
$cos θ = 1$	$sec θ = 1$
$tan θ = 0$	$cot θ = undefined$

$sin θ = 1$	$csc θ = 1$
$cos θ = 0$	$sec θ = undefined$
$tan θ = undefined$	$cot θ = 0$

$sin θ = \frac{\sqrt{3}}{2}$	$csc θ = \frac{2 \sqrt{3}}{3}$
$cos θ = - \frac{1}{2}$	$sec θ = - 2$
$tan θ = - \sqrt{3}$	$cot θ = - \frac{\sqrt{3}}{3}$

$sin θ = - \frac{\sqrt{2}}{2}$	$csc θ = - \sqrt{2}$
$cos θ = - \frac{\sqrt{2}}{2}$	$sec θ = - \sqrt{2}$
$tan θ = 1$	$cot θ = 1$