Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
He gives strength to the weary and increases the power of the weak. Isaiah 40:29 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.6.3
In American Football, the quarterback tries to throw the ball to a wide receiver. The equation to model this is \(R = \frac{v^2 \sin 2θ}{32}\) where R is the distance in feet, v is the speed the ball is thrown in feet/second, and θ is the angle above the horizontal that the ball is thrown. If the distance to the receiver and the speed of the throw are known, then the angle that the quarterback has to throw the ball can be calculated.
The general method to solve trigonometric equations is to isolate a trigonometric expression. This can be done by factoring, using trigonometric identities, or other problem solving techniques.
After the trigonometric expression is isolated, find the angles that satisfy the trigonometric expression. Remember that each trigonometric function is positive in two quadrants and negative in two quadrants, so there are usually at least two solutions for each trigonometric equation. Because trigonometric functions are periodic, there are an infinite number of solutions that can be found by adding the period of the function.
After the trigonometric expression is isolated, find the angles that satisfy the trigonometric expression. If the results are on the unit circle,
Find all solutions of 2 sin x − 1 = 0.
Solution
There is only one trigonometric function, so isolate it and solve.
2 sin x − 1 = 0
2 sin x = 1
$$\sin x = \frac{1}{2}$$
Think of the angles on the unit circle where \(\sin x = \frac{1}{2}\).
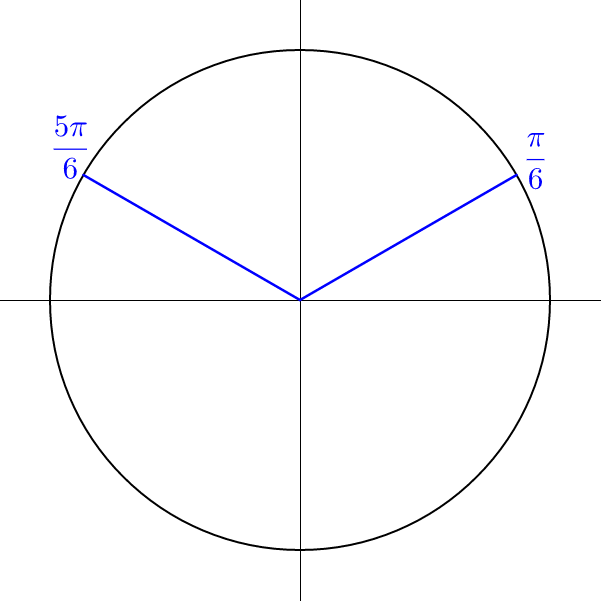
The angles are \(x = \frac{π}{6}, \frac{5π}{6}\). These are not spaced evenly, so add the period times n.
All the solutions are \(x = \frac{π}{6} + 2πn\) and \(\frac{5π}{6} + 2πn\).
Solve \(2 \cos α + \sqrt{2} = 0\).
Answer
\(\frac{3π}{4} + 2πn, \frac{5π}{4} + 2πn\)
Find all solutions of sin x tan x + sin x = 0.
Solution
Begin by factoring out the common factor, sin x.
sin x tan x + sin x = 0
sin x (tan x + 1) = 0
Apply the zero product property and set each factor equal to zero and solve.
| sin x = 0 | tan x + 1 = 0 |
| tan x = −1 | |
| Find the solutions on the unit circle | |
| x = 0, π | $$x = \frac{3π}{4}, \frac{7π}{4}$$ |
 |
 |
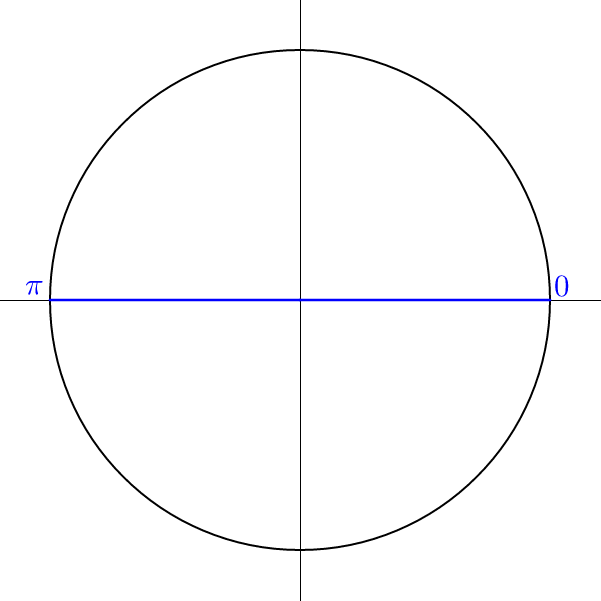
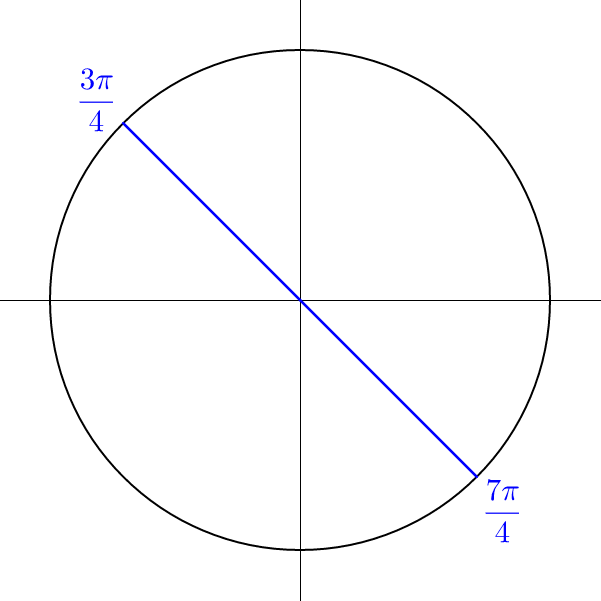
| Both sets of solutions are spaced evenly around the unit circle with π between them. | |
| x = 0 + πn | $$x = \frac{3π}{4} + πn$$ |
| x = πn | |
The solutions are \(x = πn, \frac{3π}{4} + πn\).
Solve tan x sec x − tan x = 0.
Answer
πn
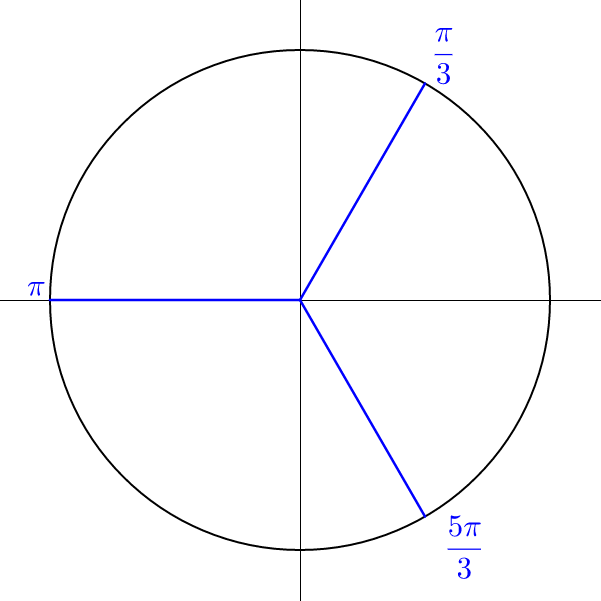
Find all solutions of 2 cos2 α + cos α − 1 = 0.
Solution
This is a quadratic type equation, so factor it as you would quadratic trinomial.
2 cos2 α + cos α − 1 = 0
(2 cos α − 1)(cos α + 1) = 0
Set each factor equal to zero and solve.
| (2 cos α − 1) = 0 | (cos α + 1) = 0 |
| $$\cos α = \frac{1}{2}$$ | cos α = −1 |
| $$α = \frac{π}{3}, \frac{5π}{3}$$ | α = π |
 |
 |
 |
|
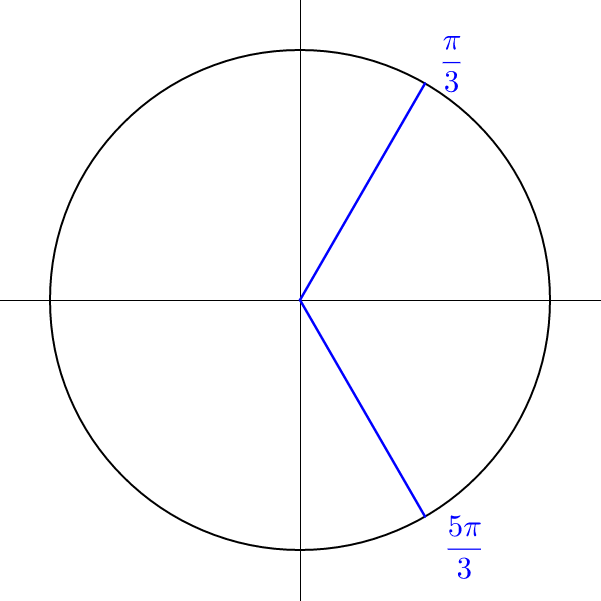
These solutions are evenly spaced around the unit circle with \(\frac{2π}{3}\) between each angle, so the solutions can be written as \(α = \frac{π}{3} + \frac{2πn}{3}\).
Solve 2 sin2 x − sin x − 1 = 0.
Answer
\(\frac{π}{2} + \frac{2πn}{3}\)
Find all the solutions on the interval [0, 2π) of sec2 β + tan2 β = 7.
Solution
A Pythagorean identity allows the substitution of tan2 β + 1 for sec2 β.
sec2 β + tan2 β = 7
tan2 β + 1 + tan2 β = 7
2 tan2 β + 1 = 7
2 tan2 β = 6
tan2 β = 3
$$\tan β = ±\sqrt{3}$$
$$β = \frac{π}{3}, \frac{2π}{3}, \frac{4π}{3}, \frac{5π}{3}$$
$$β = \frac{π}{3} + πn, \frac{2π}{3} + πn$$
Since only solutions between 0 and 2π are asked for, the solutions can be found by plugging in integers for n starting with 0 until the results are 2π or larger. This gives solutions of \(β = \frac{π}{3}, \frac{2π}{3}, \frac{4π}{3}, \frac{5π}{3}\).
Solve on the interval [0, 2π): sin2 x − cos2 x = 0.
Answer
\(\frac{π}{4}, \frac{3π}{4}, \frac{5π}{4}, \frac{7π}{4}\)
Find all the solutions on the interval [0, 2π) of sec 2θ cot 2θ = 1.
Solution
Because the trigonometric expressions do not equal 0, we cannot use the zero product property, so the expression will have to be simplified. Try rewriting the expression in terms of sine and cosine.
sec 2θ cot 2θ = 1
$$\frac{1}{\cos 2θ} \frac{\cos 2θ}{\sin 2θ} = 1$$
$$\frac{1}{\sin 2θ} = 1$$
1 = sin 2θ
The angle in the equation is 2θ.
$$2θ = \frac{π}{2} + 2πn$$
$$θ = \frac{π}{4} + πn$$
Plug in integers starting with 0 for n until the results are 2π or higher.
$$θ = \frac{π}{4}, \frac{5π}{4}$$
Solve on the interval [0, 2π): \(2\cos 3x = \sqrt{3}\).
Answer
\(\frac{π}{18}\) \(\frac{11π}{18}\), \(\frac{13π}{18}\), \(\frac{23π}{18}\), \(\frac{25π}{18}\), \(\frac{35π}{18}\)
Find all the solutions on the interval [0, 2π) of csc 3x + cot 3x = 1.
Solution
Cosecant, cotangent, and 1 are related with a Pythagorean identity, but the problem does not have squares on the trigonometric functions. To fix this, move the cotangent to other side of the equation and square both sides.
csc 3x + cot 3x = 1
csc 3x = 1 − cot 3x
csc2 3x = (1 − cot 3x)2
csc2 3x = 1 − 2 cot 3x + cot2 3x
Apply the Pythagorean identity for cosecant and cotangent to the csc2 3x. That way cotangent will be the only trigonometric function in the equation.
1 + cot2 3x = 1 − 2 cot 3x + cot2 3x
Subtract 1 and cot2 3x from both sides.
0 = −2 cot 3x
0 = cot 3x
The angle in the equation is 3x.
$$3x = \frac{π}{2} + πn$$
$$x = \frac{π}{6} + \frac{πn}{3}$$
Plug in integers starting with 0 for n until the results are 2π or higher.
$$x = \frac{π}{6}, \frac{π}{2}, \frac{5π}{6}, \frac{7π}{6}, \frac{3π}{2}, \frac{11π}{6}$$
Because both sides were squared earlier in this process, extraneous solutions were introduced. Thus, all the solutions need to be checked. Substitute each of the solutions into the original equation to see if both sides are equal. Of the possible solutions, only the following are actually solutions after checking.
$$x = \frac{π}{6}, \frac{5π}{6}, \frac{3π}{2}$$
Solve on the interval [0, 2π): cos 2x – sin 2x = 1.
Answer
0, \(\frac{3π}{4}\), π, \(\frac{7π}{4}\)
Use a graphing utility to find all the solutions in the interval [0, 2π) to three decimal places of tan x = csc x.
Solution
Make the equation equal 0, tan x − csc x = 0. Then graph the expression. Use the calculate zero feature to find the x-intercepts.
On a TI graphing calculator, press o and type in the expression. To enter csc x, type \(\frac{1}{\sin x}\). Then press q and choose ZTrig from the menu. This gives a nice graph on the interval [−2π, 2π]. To find the x-intercepts, press y / and choose zero from the menu. Use the left and right arrow keys to move the cursor to the left of an intercept and press enter. Then move the cursor to the right of the intercept and press enter. Finally move the cursor to the approximate intercept to make a guess and press enter. The intercept will be displayed on the bottom of the screen.
On a NumWorks calculator, choose Grapher from the Home screen. Enter the equation after it is solved for 0, tan x − csc x = 0. Enter csc x as \(\frac{1}{\sin x}\). Go to the Graph tab. Press O. Select Find, then Zeros. Use the left and right arrow keys to see all the zeros.
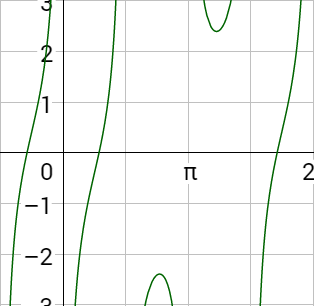
The x-intercepts and solutions are x = 0.905 and x = 5.379.
Solve on the interval [0, 2π) using a graphing utility: sin2 x + sin x = 0.
Answer
0, 3.142, 4.712
After the trigonometric expression is isolated, find the angles that satisfy the trigonometric expression. If the results are on the unit circle,
Helpful videos about this lesson.