Precalculus by Richard Wright

Previous Lesson Table of Contents Next Lesson

Are you not my student and
has this helped you?

This book is available
to download as an epub.


Whoever loves money never has enough; whoever loves wealth is never satisfied with their income. This too is meaningless. Ecclesiastes 5:10 NIV

5-03 Verify Trigonometric Identities

Mr. Wright teaches the lesson.

Summary: In this section, you will:

SDA NAD Content Standards (2018): PC.5.1

Shadow
Shadow. (pixabay/StockSnap)

The length of a shadow can be calculated from a complex trigonometric function based on the angle of elevation of the sun. Trigonometric identities can be used to simplify the function.

Verify Trigonometric Identities

To verify trigonometric identities, use the fundamental identities to simplify one side of the identity to make it look like the other side of the equation.

Things to Try for Verifying Identities

Verify a Trigonometric Identity

Verify (1 − tan α)(1 + tan α) = 2 − sec2 α.

Solution

The left side is more complicated, so start with that side.

(1 − tan α)(1 + tan α) = 2 − sec2 α

Multiply.

1 − tan2 α = 2 − sec2 α

Pythagorean identity tan2 u + 1 = sec2 u solved for tangent tan2 u = sec2 u − 1.

1 − (sec2 α − 1) = 2 − sec2 α

Simplify.

2 − sec2 α = 2 − sec2 α

Note:

Graph both sides of the identity on the same coordinate plane. The graphs will be identical if it is an identity.

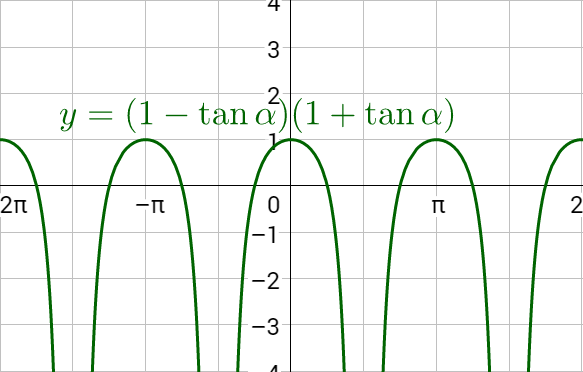
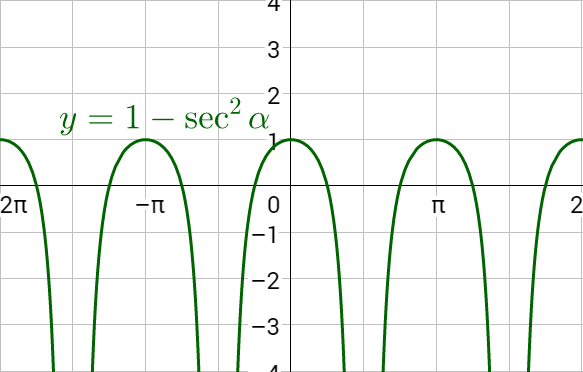
Both sides of the identity give the same graph.

Verify a Trigonometric Identity

Verify sin2 x − sin4 x = cos2 x − cos4 x

Solution

Both sides are equally complicated, so either side will be a good starting point. Let’s start with the right side.

sin2 x − sin4 x = cos2 x − cos4 x

Factor out cos2 x.

sin2 x − sin4 x = cos2 x(1 − cos2 x)

Use the Pythagorean identity (sin2 u + cos2 u = 1) solved for cos2 u (cos2 u = 1 − sin2 u).

sin2 x − sin4 x = (1 − sin2 x)(1 − (1 − sin2 x))

Simplify.

sin2 x − sin4 x = (1 − sin2 x)(sin2 x)

Multiply.

sin2 x − sin4 x = sin2 x − sin4 x

Verify tan4 x − sec4 x = −1 − 2 tan2 x.

Answer

Answers will very.

Verify a Trigonometric Identity

Verify \(\frac{\tan^2 x}{\sec x} = \sec x - \cos x\).

Solution

Left side will be easier to work with.

$$\frac{\tan^2 x}{\sec x} = \sec x - \cos x$$

Use the Pythagorean identity (1 + tan2 u = sec2 u) solved for tan2 u (tan2 u = sec2 u − 1).

$$\frac{\textcolor{blue}{\sec^2 x - 1}}{\sec x} = \sec x - \cos x$$

Separate the fraction into two fractions.

$$\frac{\textcolor{red}{\sec^2 x}}{\sec x} - \frac{\textcolor{red}{1}}{\sec x} = \sec x - \cos x$$

Simplify the fractions and \(\frac{1}{\sec x} = \cos x\).

sec x − cos x = sec x − cos x

Verify a Trigonometric Identity

Verify \(\frac{1}{\csc x\cot x} = \sec x - \cos x\).

Solution

The left is slightly more complicated, so start there.

$$\frac{1}{\csc x\cot x} = \sec x - \cos x$$

Since the fraction is \(\frac{1}{something}\) it looks like a reciprocal. Use the reciprocal identities.

sin x tan x = sec x − cos x

An identity that relates tangent and sine is \(\tan u = \frac{\sin u}{\cos u}\).

$$\sin x \textcolor{red}{\frac{\sin x}{\cos x}} = \sec x - \cos x$$

$$\frac{\textcolor{red}{\sin^2 x}}{\cos x} = \sec x - \cos x$$

Use the Pythagorean identity sin2 u + cos2 u = 1 to substitute for sin2 x.

$$\frac{\textcolor{green}{1 - \cos^2 x}}{\cos x} = \sec x - \cos x$$

Separate the fraction into two fractions.

$$\frac{\textcolor{brown}{1}}{\cos x} - \frac{\textcolor{brown}{\cos^2 x}}{\cos x} = \sec x - \cos x$$

Simplify the fractions and \(\frac{1}{\cos x} = \sec x\).

sec x − cos x = sec x − cos x

Verify \(\frac{1}{\cos x \tan x} = \csc x\)

Answer

Answers will very.

Verify a Trigonometric Identity

Verify sin(−θ)sec(−θ) = −tan θ.

Solution

The left side will be easier to work with.

sin(−θ)sec(−θ) = −tan θ

Use the even/odd identities (sin(−u) = −sin u and sec(−u) = sec u).

−sin θ sec θ = −tan θ

Use the reciprocal identity (\(\sec u = \frac{1}{\cos u}\)) to rewrite sec θ.

$$-\sin θ \textcolor{red}{\frac{1}{\cos θ}} = -\tan θ$$

$$-\frac{\sin θ}{\cos θ} = -\tan θ$$

Use the quotient identity (\(\tan u = \frac{\sin u}{\cos u}\)).

−tan θ = −tan θ

Verify a Trigonometric Identity

Verify \(\frac{\sin x + \tan y}{\sin x \tan y} = \cot y + \csc x\).

Solution

Again the left side is more complex.

$$\frac{\sin x + \tan y}{\sin x \tan y} = \cot y + \csc x$$

Separate the fraction into two fractions.

$$\frac{\textcolor{blue}{\sin x}}{\sin x \tan y} + \frac{\textcolor{blue}{\tan y}}{\sin x \tan y} = \cot y + \csc x$$

Simplify.

$$\textcolor{red}{\frac{1}{\tan y}} + \textcolor{red}{\frac{1}{\sin x}} = \cot y + \csc x$$

Use reciprocal identities (\(\cot u = \frac{1}{\tan u}\) and \(\csc u = \frac{1}{\sin u}\)).

cot y + csc x = cot y + csc x

Verify \(\tan\left(\frac{π}{2} - x\right)\sin \left(-x\right) = -\cos x\).

Answer

Answers will very.

Verify a Trigonometric Identity

Verify \(1 - \sin^2\left(\frac{π}{2} - x\right) = \sin^2 x\) a) algebraically and b) graphically.

Solution

  1. The left side is again the most complex.

    $$1 - \sin^2\left(\frac{π}{2} - x\right) = \sin^2 x$$

    Use the cofunction identity (\(\sin\left(\frac{π}{2} - u\right) = \cos u\)).

    1 − cos2 x = sin2 x

    Use the Pythagorean identity (sin2 u + cos2 u = 1) solve for sin2 u (sin2 u = 1 − cos2 u).

    sin2 x = sin2 x

  2. Graph the left side of the equation, then graph the right side of the equation and notice that they are the same.

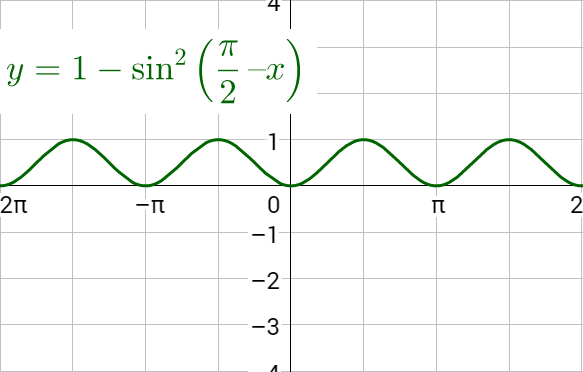
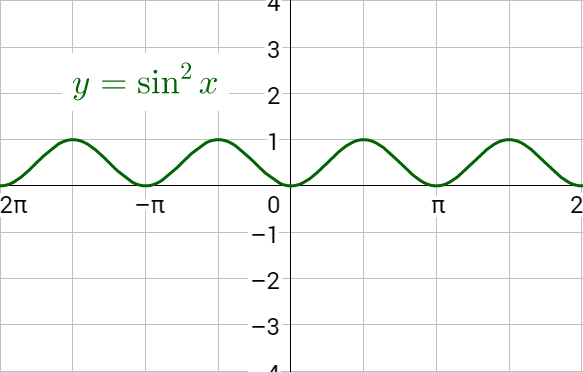
    Both sides of the identity give the same graph.

Verify \(\frac{\sec x - \csc x}{\sec x \csc x} = \sin x - \cos x\) both (a) algebraically and (b) graphically.

Answers

Answers will very;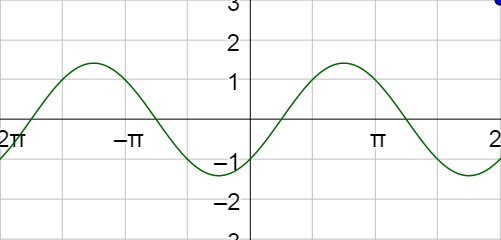

Lesson Summary
Things to Try for Verifying Identities

Helpful videos about this lesson.

Practice Exercises

  1. Derive the other two Pythagorean identities from sin2 u + cos2 u = 1.
  2. Verify the identities.
  3. (1 − cos t)(1 + cos t) = sin2 t
  4. (csc α + 1)(csc α − 1) = cot2 α
  5. cos x − cos3 x = cos x sin2 x
  6. sin4 x − cos4 x = 1 − 2 cos2 x
  7. \(\frac{\sin x - 1}{\cos x} = \tan x - \sec x\)
  8. \(\frac{\csc^2 x}{\tan x} = \cot x + \cot^3 x\)
  9. \(\frac{1}{\cos x \sin x} = \cot x + \tan x\)
  10. tan(−t)cos(−t)cot(−t) = cos t
  11. \(\sin\left(-x\right)\csc\left(\frac{π}{2} - x\right) = -\tan x\)
  12. \(\frac{\cos x + \cot y}{\cos x \cot y} = \sec x + \tan y\)
  13. \(\frac{1}{1 - \sin x} + \frac{1}{1 + \sin x} = 2\sec^2 x\)
  14. Verify the identity algebraically and graphically.
  15. \(\tan\left(\frac{π}{2} - x\right)\tan x = 1\)
  16. sin4 x = sin2 x − sin2 x cos2 x

  17. The length, ℓ, of a shadow cast by a vertical stick of height, h, when the angle of elevation of the sun is θ can be modeled by

    $$ℓ = \frac{h \cos θ}{\cos\left(90° - θ\right)}$$

    Verify that ℓ = h cot θ.

  18. Mixed Review
  19. (5-02) Factor and then use the fundamental trigonometric identities to simplify: sin4 x − 2 sin2 x + 1.
  20. (5-02) Rewrite the fraction so it is not in fractional form: \(\frac{3}{\csc x \tan x}\).
  21. (5-01) Simplify: sin x (csc x − sin x).
  22. (4-02) List all the angles, θ, on the unit circle where \(\sin θ = ±\frac{\sqrt{3}}{2}\).
  23. (3-03) Condense: log 2x + 3 log x − 4 log y.

Answers

  1. a) \(\sin^2 u + \cos^2 u = 1\) → \(\frac{\sin^2 u + \cos^2 u}{\sin^2 u} = \frac{1}{\sin^2 u}\) → \(1 + \cot^2 u = \csc^2 u\); b) \(\sin^2 u + \cos^2 u = 1\) → \(\frac{\sin^2 u + \cos^2 u}{\cos^2 u} = \frac{1}{\cos^2 u}\) → \(\tan^2 u + 1 = \sec^2 u\)
  2. \(\left(1 - \cos t\right)\left(1 + \cos t\right) =\) \(1 - \cos^2 t =\) \(\sin^2 t\)
  3. \(\left(\csc α +1\right)\left(\csc α - 1\right) =\) \(\csc^2 α - 1 =\) \(\left(\cot^2 α + 1\right) - 1 =\) \(\cot^2 α\)
  4. \(\cos x - \cos^3 x =\) \(\cos x\left(1 - \cos^2 x\right) =\) \(\cos x \sin^2 x\)
  5. \(\sin^4 x - \cos^4 x =\) \(\left(\sin^2 x - \cos^2 x\right)\left(\sin^2 x + \cos^2 x\right) =\) \(\left(\sin^2 x - \cos^2 x\right)\left(1\right) =\) \(\sin^2 x - \cos^2 x =\) \(1 - \cos^2 x - \cos^2 x =\) \(1 - 2\cos^2 x\)
  6. \(\frac{\sin x - 1}{\cos x} =\) \(\frac{\sin x}{\cos x} - \frac{1}{\cos x} =\) \(\tan x - \sec x\)
  7. \(\frac{\csc^2 x}{\tan x} =\) \(\frac{1 + \cot^2 x}{\tan x} =\) \(\frac{1}{\tan x} + \frac{\cot^2 x}{\tan x} =\) \(\cot x + \cot^3 x\)
  8. \(\frac{1}{\cos x \sin x} =\) \(\frac{\cos x}{\cos^2 x \sin x} =\) \(\sec^2 x \cot x = \) \(\frac{\sec^2 x}{\tan x} =\) \(\frac{1 + \tan^2 x}{\tan x} =\) \(\frac{1}{\tan x} + \frac{\tan^2 x}{\tan x} =\) \(\cot x + \tan x\)
  9. \(\tan\left(-t\right)\cos\left(-t\right)\cot\left(-t\right) =\) \(\tan\left(-t\right)\cot\left(-t\right)\cos\left(-t\right) =\) \(\cos\left(-t\right) =\) \(\cos t\)
  10. \(\sin\left(-x\right)\csc\left(\frac{π}{2} - x\right) =\) \(-\sin x \sec x =\) \(-\frac{\sin x}{\cos x} =\) \(-\tan x\)
  11. \(\frac{\cos x + \cot y}{\cos x \cot y} =\) \(\frac{\cos x}{\cos x \cot y} + \frac{\cot y}{\cos x \cot y} =\) \(\frac{1}{\cot y} + \frac{1}{\cos x} =\) \(\sec x + \tan y\)
  12. \(\frac{1}{1 - \sin x} + \frac{1}{1 + \sin x} =\) \(\frac{1 + \sin x}{\left(1 - \sin x\right)\left(1 + \sin x\right)} + \frac{1 - \sin x}{\left(1 - \sin x\right)\left(1 + \sin x\right)} =\) \(\frac{2}{1 - \sin^2 x} =\) \(\frac{2}{\cos^2 x} =\) \(2\sec^2 x\)
  13. \(\tan\left(\frac{π}{2} - x\right)\tan x =\) \(\cot x \tan x =\) \(1\)
  14. \(\sin^4 x =\) \(\sin^2 x \sin^2 x =\) \(\sin^2 x\left(1 - \cos^2 x\right) =\) \(\sin^2 x - \sin^2 x \cos^2 x\)
  15. \(ℓ = \frac{h \cos θ}{\cos\left(90° - θ\right)} =\) \(\frac{h \cos θ}{\sin θ} =\) \(h \cot θ\)
  16. cos4 x
  17. 3 cos x
  18. cos2 x
  19. \(\frac{π}{3}, \frac{2π}{3}, \frac{4π}{3}, \frac{5π}{3}\)
  20. \(\log \frac{2x^4}{y^4}\)