Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
In the beginning was the Word, and the Word was with God, and the Word was God. He was with God in the beginning. John 1:1-2 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.6.3
Part of geometry and simple trigonometry was originally developed in Egypt to find the boundaries of fields. Every year the Nile River would flood in the spring and the farmers needed a way locate their fields after the water level dropped. Triangles were an integral part of finding the field boundaries. Trigonometry has advanced greatly in the last few thousand years, but it is still used to survey land.
To solve any triangle, you need to know the length of at least one side and two other parts. If one of the other parts is a right angle, then sine, cosine, tangent, and the Pythagorean theorem can be used to solve it. For an oblique triangle, the law of sines or law of cosines (lesson 6-02) must be used. Use the law of sines if two angles and a side are known (ASA or AAS) or two sides and an opposite angle are known (SSA).
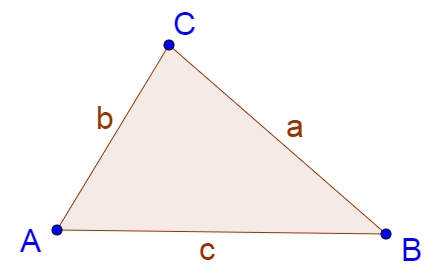
For convenience, when labeling a triangle, the side opposite an angle is named with the same letter, but lowercase.
$$\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}$$
Use for ASA, AAS, or SSA cases.
Solve ∆ABC where A = 20°, B = 60°, and a = 10.
Solution
It is often easier to draw the triangle and label it as solutions are found.
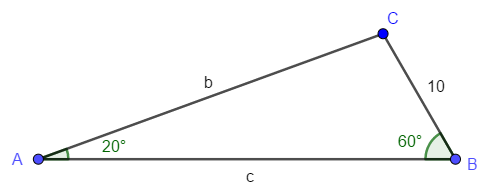
Since A, a, and B are known, side b could easily be found with the first two parts of the law of sines.
$$\frac{\sin A}{a} = \frac{\sin B}{b}$$
$$\frac{\sin 20°}{10} = \frac{\sin 60°}{b}$$
Cross multiply.
b sin 20° = 10 sin 60°
$$b = \frac{10 \sin 60°}{\sin 20°}$$
b ≈ 25.32
Now, find the c’s. Angle C can be found using the fact that the sum of the angles of a triangle is 180°.
C = 180° – 20° – 60°
C = 100°
Finally, use the law of sines to find side c. Use A and a since their exact values are known and thus there will not be any rounding error.
$$\frac{\sin A}{a} = \frac{\sin C}{c}$$
$$\frac{\sin 20°}{10} = \frac{\sin 100°}{c}$$
$$c \sin 20° = 10 \sin 100°$$
$$c = \frac{10 \sin 100°}{\sin 20°}$$
c ≈ 28.79
Solve ∆LMN where L = 30°, M = 40°, and n = 12.
Solution
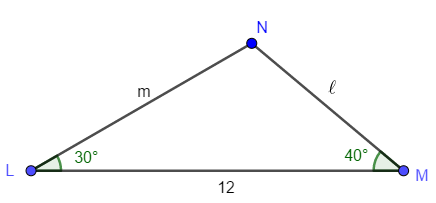
To use the law of sines, an angle and opposite side must be known. For this triangle, that means angle N is needed.
N = 180° – L – M
N = 180° – 30° – 40°
N = 110°
Now, use N and n to find a side using the law of sines.
$$\frac{\sin N}{n} = \frac{\sin L}{ℓ}$$
$$\frac{\sin 110°}{12} = \frac{\sin 30°}{ℓ}$$
$$ℓ \sin 110° = 12 \sin 30°$$
$$ℓ = \frac{12 \sin 30°}{\sin 110°}$$
ℓ ≈ 6.39
Now, use N and n to find the other side using the law of sines.
$$\frac{\sin N}{n} = \frac{\sin M}{m}$$
$$\frac{\sin 110°}{12} = \frac{\sin 40°}{m}$$
$$m \sin 110° = 12 \sin 40°$$
$$m = \frac{12 \sin 40°}{\sin 110°}$$
m ≈ 8.21
Solve ΔABC where A = 20°, B = 110°, and c = 25.
Answer
C = 50°, a = 11.16, b = 30.67
Remember back to geometry. There were several theorems to prove triangles congruent such as ASA and AAS. Congruence theorems mean that there is only one triangle possible with that combination of sides and angles. While ASA and AAS were congruence theorems, SSA was not. That is because when two sides and a nonincluded angle are known, there is the a possibility of 0, 1, or 2 triangles with that combination of sides and angles. Thus SSA is known as the ambiguous case.
In order to solve SSA triangles, the first thing to do is calculate the number of triangles for the combination of sides and angle.
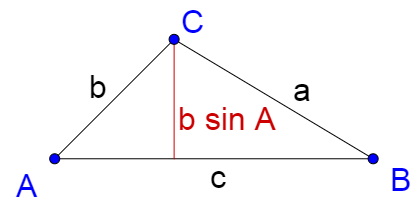
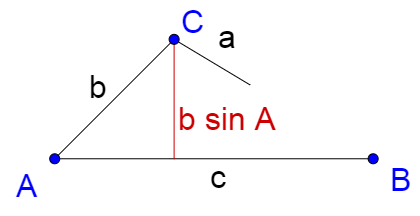
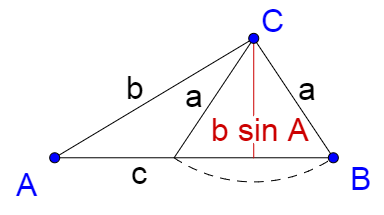
Solve ∆RST given R = 120°, r = 10, and s = 8.
Solution
First, find the number of solutions. In this triangle R is equivalent to A, r to a, and s to b. R > 90° and r > s, so there is 1 solution.
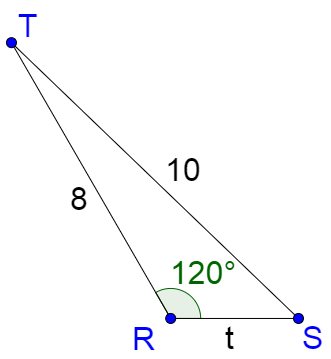
Use the law of sines to solve for S.
$$\frac{\sin R}{r} = \frac{\sin S}{s}$$
$$\frac{\sin 120°}{10} = \frac{\sin S}{8}$$
$$10 \sin S = 8 \sin 120°$$
$$\sin S = \frac{8 \sin 120°}{10}$$
$$\sin S = \frac{2\sqrt{3}}{5}$$
$$S = \sin^{-1} \frac{2\sqrt{3}}{5}$$
S ≈ 43.85°
Now, find the third angle, T.
T = 180° – R – S
T ≈ 180° – 120° – 43.85°
T ≈ 16.15°
Now, use the law of sines to find the last side, t.
$$\frac{\sin R}{r} = \frac{\sin T}{t}$$
$$\frac{\sin 120°}{10} = \frac{\sin 16.15°}{t}$$
$$t \sin 120° = 10 \sin 16.15°$$
$$t = \frac{10 \sin 16.15°}{\sin 120°}$$
t ≈ 3.21
Solve ΔABC where A = 50°, a = 60, and b = 40.
Answer
B = 30.71°, C = 99.29°, c = 77.30
Solve ∆XYZ where Y = 50°, y = 8, and z = 9.
Solution
First find the number of solutions. In this triangle Y is equivalent A, y to a, and z to b. Y < 90° and all the choices depend on b sin A or z sin Y ≈ 6.89, so z sin Y < y < z which is equivalent to b sin A < a < b. That means there are two solutions.
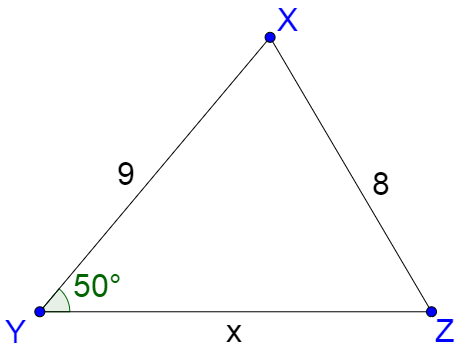
To solve the first triangle, use the law of sines as was done for the previous examples. Start by finding Z.
$$\frac{\sin Y}{y} = \frac{\sin Z}{z}$$
$$\frac{\sin 50°}{8} = \frac{\sin Z}{9}$$
$$8 \sin Z = 9 \sin 50°$$
$$\sin Z = \frac{9 \sin 50°}{8}$$
$$Z = \sin^{-1} \frac{9 \sin 50°}{8}$$
Z ≈ 59.52°
Now, find the third angle.
X = 180° – Y – Z
X ≈ 180° – 50° – 59.52°
X ≈ 70.48°
Lastly, find the third side.
$$\frac{\sin Y}{y} = \frac{\sin X}{x}$$
$$\frac{\sin 50°}{8} = \frac{\sin 70.48°}{x}$$
$$x \sin 50° = 8 \sin 70.48°$$
$$x = \frac{8 \sin 70.48°}{\sin 50°}$$
x ≈ 9.84
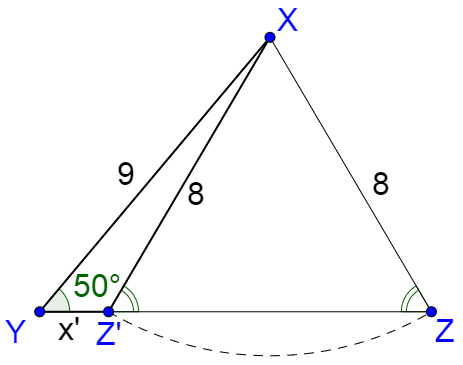
For the second solutions, prime symbols are used: Z', X', and x'.
To solve the 2nd triangle, think of swinging side y to form an obtuse triangle ∆YXZ'. The triangle ∆ZXZ' is an isosceles triangle where the base angles are congruent. The angles on both sides of Z' are a linear pair and supplementary. Thus m∠YZ'X = 180° – m∠Z.
Z' = 180° – Z
Z' = 180° – 59.52°
Z' ≈ 120.48°
Find the third angle, X'.
X' = 180° – Y – Z'
X' = 180° – 50° – 120.48°
X' ≈ 9.52°
Now, find the third side, x'.
$$\frac{\sin Y}{y} = \frac{\sin X'}{x'}$$
$$\frac{\sin 50°}{8} = \frac{\sin 9.52°}{x'}$$
$$x' \sin 50° = 8 \sin 9.52°$$
$$x' = \frac{8 \sin 9.52°}{\sin 50°}$$
x' ≈ 1.73
Solve ΔABC where A = 50°, a = 35, and b = 40.
Answer
1st Solution: B = 61.10°, C = 68.90°, c = 42.63; 2nd Solution: B = 118.90°, C = 11.10°, c = 8.80
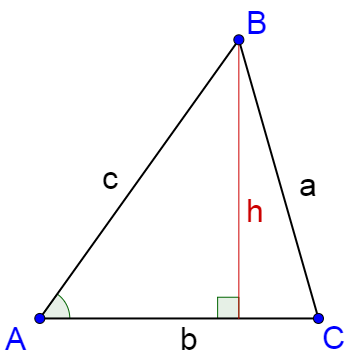
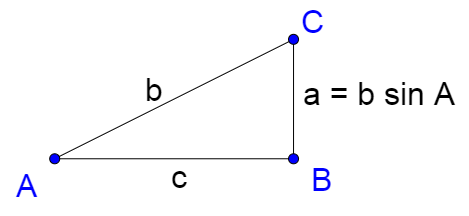
The area of a triangle is calculated by
$$Area = \frac{1}{2} bh$$
The height of the triangle is found using the left triangle.
$$\sin A = \frac{h}{c}$$
$$h = c \sin A$$
Substitute this into the area formula.
$$Area = \frac{1}{2} bc \sin A$$
$$Area = \frac{1}{2} bc \sin A$$
$$Area = \frac{1}{2} ac \sin B$$
$$Area = \frac{1}{2} ab \sin C$$
Find the area of ∆FGH where F = 30°, g = 4, h = 8.
Solution
$$Area = \frac{1}{2} gh \sin F$$
$$Area = \frac{1}{2} \left(4\right)\left(8\right) \sin 30°$$
$$Area = 8$$
Find the area of ΔABC where C = 50°, a = 60, and b = 40.
Answer
919.25
$$\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}$$
Use for ASA, AAS, or SSA cases.
$$Area = \frac{1}{2} bc \sin A$$
$$Area = \frac{1}{2} ac \sin B$$
$$Area = \frac{1}{2} ab \sin C$$
Helpful videos about this lesson.
