Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Therefore, if anyone is in Christ, the new creation has come: The old has gone, the new is here! 2 Corinthians 5:17 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.6.3
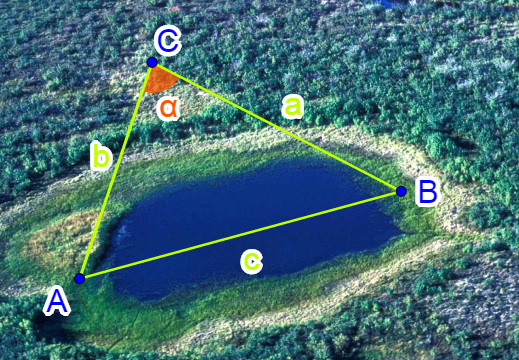
To approximate the length of an impassible swamp, a surveyor finds a point midway along the side of the swamp but at a distance where he can measure the distance to each end. He measures one distance as 235 m and the other as 290 m. The angle between the distance lines is 110°. The law of sines cannot be used to find the third side because a side and opposite angle are not known. So the surveyor will have to use the law of cosines to find the length of the swamp.
To solve a triangle, a side and two other pieces of information must be known. The law of cosines should be used when two sides and the included angle (SAS) or all three sides (SSS) are known.
Use for SAS and SSS cases
a2 = b2 + c2 − 2bc cos A
b2 = a2 + c2 − 2ac cos B
c2 = a2 + b2 − 2ab cos C
Notice that the first and last letter are the same—one a side and one an angle. The other two sides are in between.
Solve ∆ABC where A = 30°, b = 15, and c = 17.
Solution
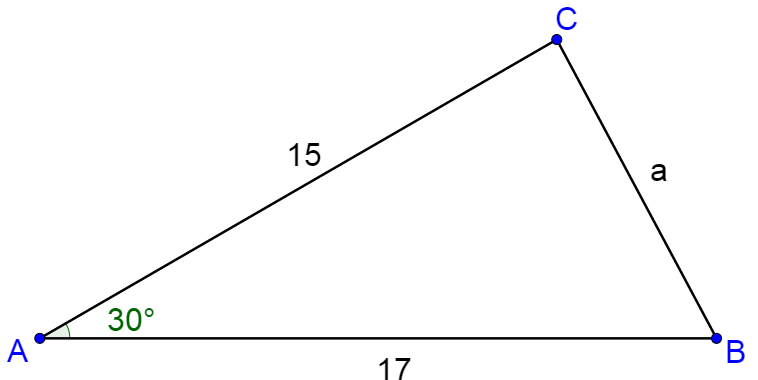
Because angle A is known, start by finding side a.
a2 = b2 + c2 − 2bc cos A
a2 = 152 + 172 − 2(15)(17) cos 30°
a2 ≈ 72.32704
a ≈ 8.50
Now, find an angle.
b2 = a2 + c2 − 2ac cos B
152 = 8.502 + 172 − 2(8.50)(17) cos B
225 = 72.25 + 289 − 289 cos B
Subtract the 72.25 and 289.
−136.25 = −289 cos B
0.4715 = cos B
B = cos−1 0.4715
B ≈ 61.87°
Lastly, subtract from 180° to find the last angle.
C = 180° – A – B
C ≈ 180° – 30° – 61.87°
C ≈ 88.13°
Solve ΔABC where B = 120°, a = 20, and c = 18.
Answer
A = 31.74°, C = 28.26°, b = 32.92
Notice in the previous example, that after finding the first side, a side and opposite angle is known. You might think that you could use the law of sines to find angle B, but that is a bad idea. If you used the law of sines, it would be the SSA case where there is a possibility of two solutions. However, because we started with SAS or SSS for law of cosines, there is only one solution since they are both geometry congruence theorems. If you start a problem with the law of cosines, you need to continue using the law of cosines. Do not switch to the law of sines!
Solve ∆RST where r = 20, s = 17, t = 24.
Solution
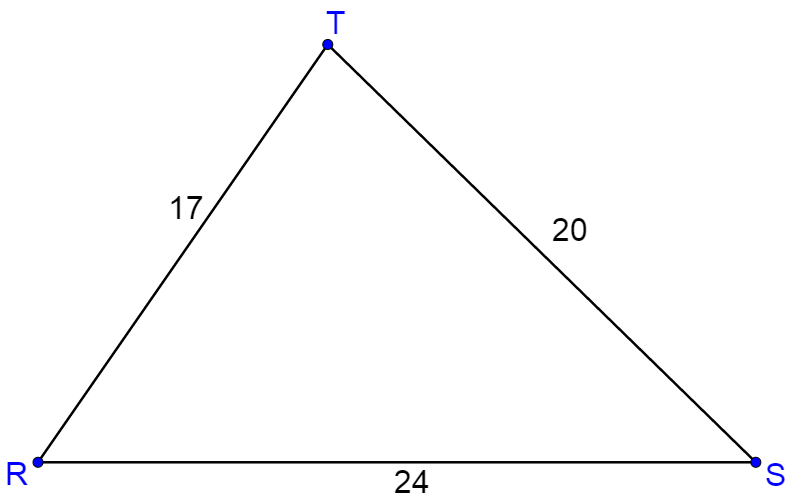
Start by finding an angle.
r2 = s2 + t2 − 2st cos R
202 = 172 + 242 − 2(17)(24) cos R
400 = 289 + 576 − 816 cos R
−465 = −816 cos R
$$\frac{155}{272} = \cos R$$
$$R = \cos^{-1} \frac{155}{272}$$
R ≈ 55.26°
Now find a second angle.
s2 = r2 + t2 − 2rt cos S
172 = 202 + 242 − 2(20)(24) cos S
289 = 400 + 576 − 960 cos S
−687 = −960 cos S
$$\frac{229}{320} = \cos S$$
$$S = \cos^{-1} \frac{229}{320}$$
S ≈ 44.31°
Subtract to find the last angle.
T = 180° – R – S
T ≈ 180° – 55.26° – 44.31°
T ≈ 80.43°
Solve ΔABC where a = 20, b = 22, and c = 18.
Answer
A = 58.99°, B = 70.53°, C = 50.48°
In the last lesson, the area of a triangle was found using two sides and an angle. The Greek mathematician, Heron, developed a formula for finding the area of a triangle when just the lengths of the sides are known.
$$Area = \sqrt{s\left(s - a\right)\left(s - b\right)\left(s - c\right)}$$
where \(s = \frac{a + b + c}{2}\)
Find the area of a triangle with side lengths 10, 12, 15.
Solution
Start by finding s.
$$s = \frac{a + b + c}{2}$$
$$s = \frac{10 + 12 + 15}{2}$$
$$s = \frac{37}{2}$$
Now use Heron’s formula
$$Area = \sqrt{\frac{37}{2}\left(\frac{37}{2} - 10\right)\left(\frac{37}{2} - 12\right)\left(\frac{37}{2} - 15\right)}$$
Area ≈ 59.81
Find the area of ΔABC where a = 20, b = 22, and c = 18.
Answer
169.71
Use for SAS and SSS cases
a2 = b2 + c2 − 2bc cos A
b2 = a2 + c2 − 2ac cos B
c2 = a2 + b2 − 2ab cos C
$$Area = \sqrt{s\left(s - a\right)\left(s - b\right)\left(s - c\right)}$$
where \(s = \frac{a + b + c}{2}\)
Helpful videos about this lesson.
