Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
God is our refuge and strength, an ever-present help in trouble. Therefore we will not fear, though the earth give way and the mountains fall into the heart of the sea. Psalms 46:1-2 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.5.3, PC.6.4
Pretend you are hiking in the woods. You know you parked a mile away, so you start walking. Is it important which direction you walk? It is if you want to get back to your car. Vectors are quantities that include direction.
A vector is a mathematical quantity with direction and magnitude. Magnitude is the size of the vector. So if your car is 1 mile to the east, the magnitude of the vector is 1 mile and the direction is east.
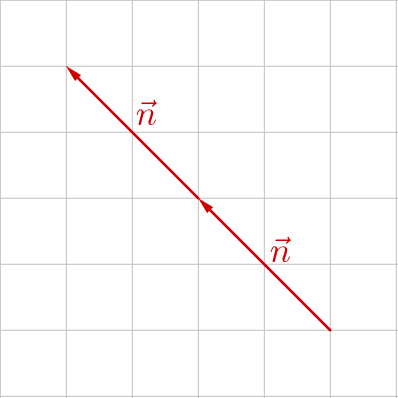
Vectors are represented by arrows. The point where the arrow starts is called the initial point and the point where the arrow ends is called the terminal point.
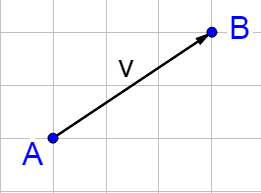
To conveniently use vectors, they are written in component form. Component form describes a vector by how far it is horizontally and vertically. These are called the horizontal and vertical components. The components are calculated by subtracting the initial point from the terminal point.
$$\overset{\rightharpoonup}{v} = \langle v_x, v_y \rangle = \langle q_x - p_x, q_y - p_y \rangle$$
The magnitude is the length of the vector arrow. This can be found with the Pythagorean theorem.
$$\lVert \overset{\rightharpoonup}{v} \rVert = \sqrt{\left(q_x - p_x\right)^2 + \left(q_y - p_y\right)^2} = \sqrt{v_x^2 + v_y^2}$$
$$\overset{\rightharpoonup}{v} = \langle v_x, v_y \rangle = \langle q_x - p_x, q_y - p_y \rangle$$
where \(\left(p_x, p_y\right)\) is the initial point and \(\left(q_x, q_y\right)\) is the terminal point.
Magnitude
$$\lVert \overset{\rightharpoonup}{v} \rVert = \sqrt{\left(q_x - p_x\right)^2 + \left(q_y - p_y\right)^2} = \sqrt{v_x^2 + v_y^2}$$
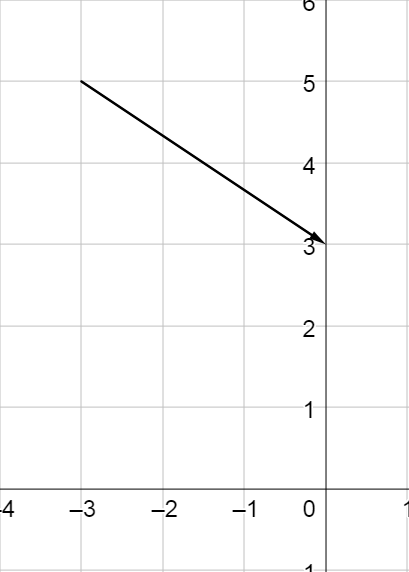
Find the (a) component form and (b) magnitude of the vector \(\overset{\rightharpoonup}{r}\) with initial point (2, 5) and terminal point (−2, 4).
Solution
$$\overset{\rightharpoonup}{r} = \langle q_x - p_x, q_y - p_y \rangle$$
$$\overset{\rightharpoonup}{r} = \langle -2 - 2, 4 - 5 \rangle$$
$$\overset{\rightharpoonup}{r} = \langle -4, -1 \rangle$$
$$\lVert \overset{\rightharpoonup}{r} \rVert = \sqrt{r_x^2 + r_y^2}$$
$$\lVert \overset{\rightharpoonup}{r} \rVert = \sqrt{\left(-4\right)^2 + \left(-1\right)^2}$$
$$\lVert \overset{\rightharpoonup}{r} \rVert = \sqrt{17}$$
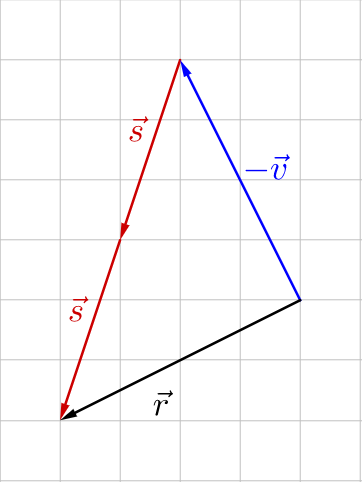
Find the (a) component form and (b) magnitude of \(\overset{\rightharpoonup}{s}\) with initial point (−2, 4) and terminal point (3, 0).
Answer
\(\overset{\rightharpoonup}{s} = \langle 5, -4 \rangle\); \(\lVert \overset{\rightharpoonup}{s} \rVert = 2\sqrt{5}\)
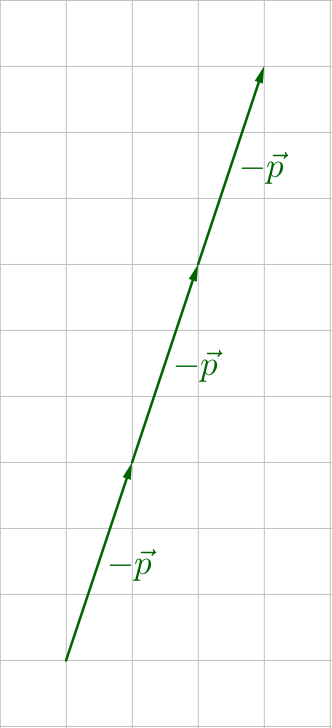
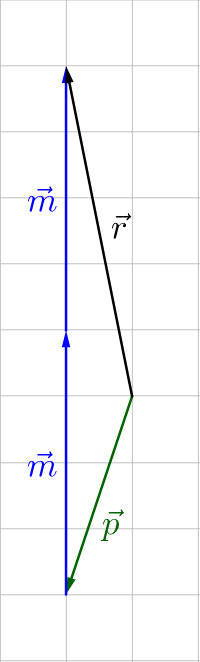
Scalar multiplication is multiplying a vector by a single number. A scalar is a quantity without direction and is not a vector. Graphically, scalar multiplication drawing several copies of the same vector end to end.
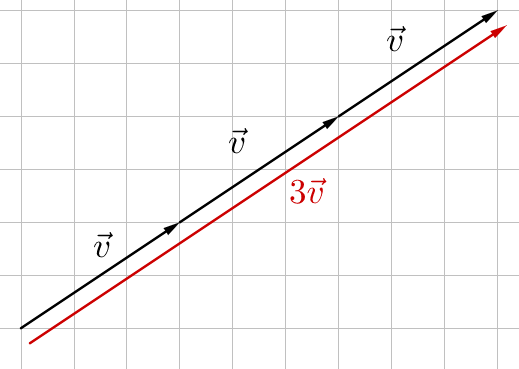
Algebraically, the scalar is distributed to each component of the vector.
$$k\overset{\rightharpoonup}{v} = \langle kv_x, kv_y \rangle$$
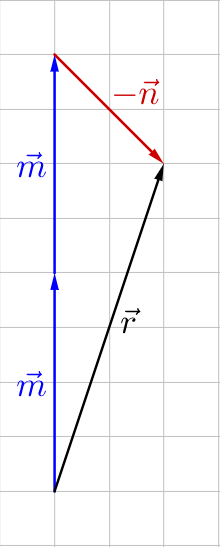
Multiplying a vector by −1 results in a vector of the same magnitude, but opposite direction.
Graphically
Algebraically
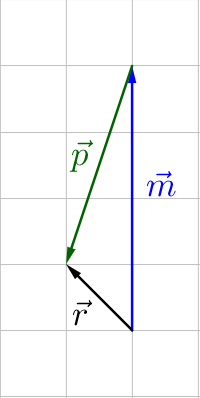
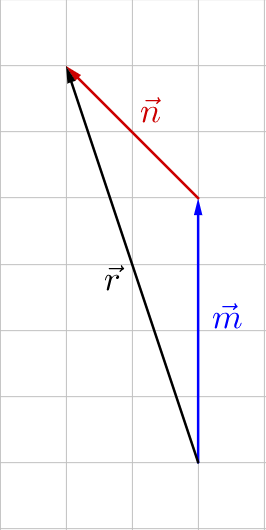
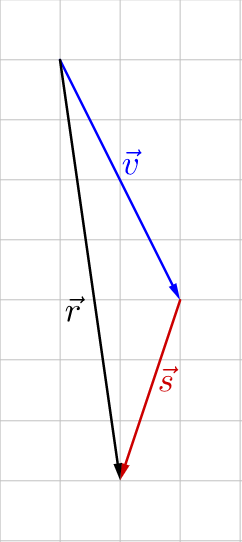
Graphically, adding vectors means to draw them tip-to-tail. This means you draw the first vector, then draw the second vector with its tail at the tip of the first vector. The resultant, or sum, is the vector from the first initial point to the final terminal point.
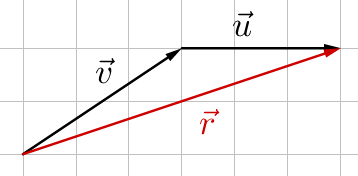
Algebraically, add vectors by adding like components. This is because the total horizontal component is the horizontal distance of the first vector and the horizontal distance of the second vector. Likewise for the vertical components.
$$\overset{\rightharpoonup}{v} + \overset{\rightharpoonup}{u} = \langle v_x + u_x, v_y + u_y \rangle$$
Graphically
Algebraically
Let \(\overset{\rightharpoonup}{u}\), \(\overset{\rightharpoonup}{v}\), and \(\overset{\rightharpoonup}{w}\) be vectors and let a and b be scalars.
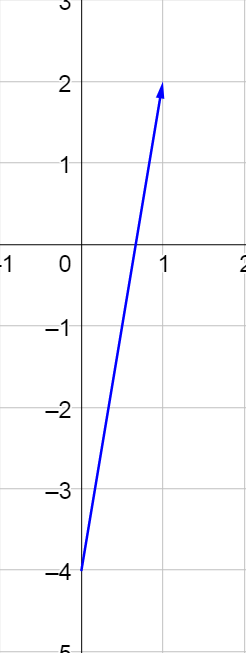
Given \(\overset{\rightharpoonup}{t} = \langle 1, 4 \rangle\), find \(3\overset{\rightharpoonup}{t}\) both (a) graphically and (b) algebraically.
Solution
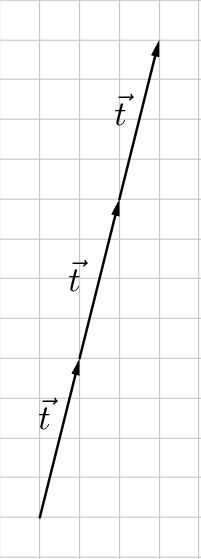
$$3\overset{\rightharpoonup}{t} = 3\langle 1, 4 \rangle$$
$$= \langle 3, 12 \rangle$$
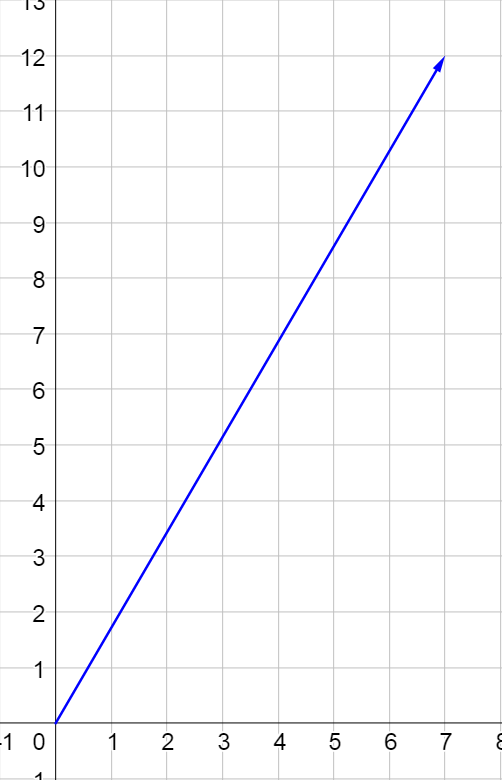
Given \(\overset{\rightharpoonup}{m} = \langle 2, 3 \rangle\) and \(\overset{\rightharpoonup}{n} = \langle -1, 1 \rangle\), find \(2\overset{\rightharpoonup}{m} + \overset{\rightharpoonup}{n}\) both (a) graphically and (b) algebraically.
Solution
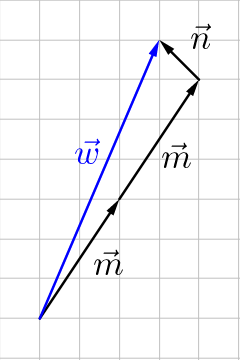
$$2\overset{\rightharpoonup}{m} + \overset{\rightharpoonup}{n} = 2\langle 2, 3 \rangle + \langle -1, 1 \rangle$$
$$= \langle 4, 6 \rangle + \langle -1, 1 \rangle$$
$$= \langle 3, 7 \rangle$$
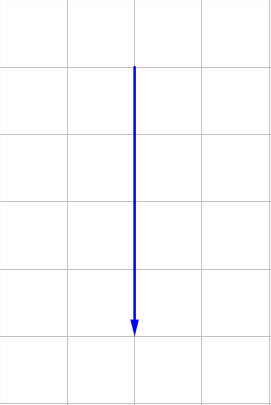
Given that \(\overset{\rightharpoonup}{t} = \langle 0, 4 \rangle\) and \(\overset{\rightharpoonup}{s} = \langle 4, -5 \rangle\), find \(\overset{\rightharpoonup}{t} + 2\overset{\rightharpoonup}{s}\) both graphically and algebraically.
Answer
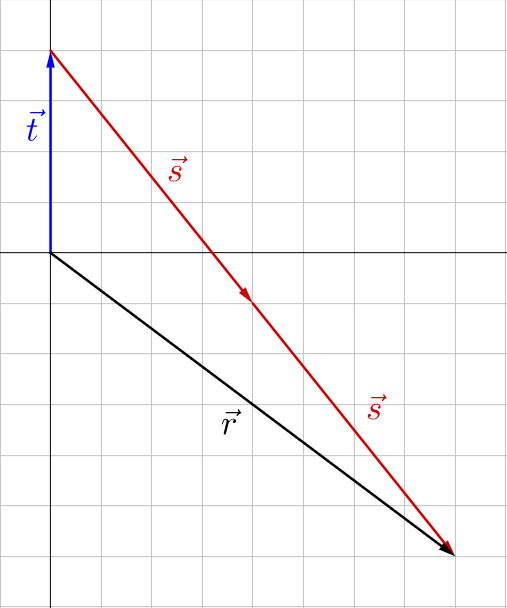; \(\langle 8, -6 \rangle\)
A unit vector is a vector whose magnitude is one. To find a unit vector in the direction of another vector, simply divide by the magnitude.
A unit vector in the direction of \(\overset{\rightharpoonup}{v}\)
$$\hat{u} = \frac{\overset{\rightharpoonup}{v}}{\lVert \overset{\rightharpoonup}{v} \rVert}$$
Find a unit vector in the direction of \(\overset{\rightharpoonup}{g} = \langle 6, -8 \rangle\).
Solution
$$\hat{u} = \frac{\overset{\rightharpoonup}{g}}{\lVert \overset{\rightharpoonup}{g} \rVert}$$
$$\hat{u} = \frac{\langle 6, -8 \rangle}{\sqrt{6^2 + \left(-8\right)^2}}$$
$$= \frac{\langle 6, -8 \rangle}{10}$$
$$= \left\langle \frac{6}{10}, -\frac{8}{10}\right\rangle$$
$$= \left\langle \frac{3}{5}, -\frac{4}{5} \right\rangle$$
Find a unit vector in the direction of \(\overset{\rightharpoonup}{b} = \langle 3, -3 \rangle\).
Answer
\(\left\langle \frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2} \right\rangle\)
There are two special unit vectors: \(\hat{i} = \langle 1, 0 \rangle\) and \(\hat{j} = \langle 0, 1 \rangle\). \(\hat{i}\) indicates the x-component and \(\hat{j}\) indicates the y-component and can be used to write vectors in linear combination form. For example, \(\langle 3, 2 \rangle = 3\hat{i} + 2\hat{j}\). The advantage of linear combination is that vector addition and scalar multiplication follows the general rules of algebra like combining like terms and the distributive property.
\(\hat{i} = \langle 1, 0 \rangle\) and signifies the x-component
\(\hat{j} = \langle 0, 1 \rangle\) and signifies the y-component
$$\langle v_x, v_y \rangle = v_x \hat{i} + v_y \hat{j}$$
Solution
\(\overset{\rightharpoonup}{v} = -2 \hat{i} + 7 \hat{j}\) and \(\overset{\rightharpoonup}{u} = \hat{i} - 5 \hat{j}\)
$$3\overset{\rightharpoonup}{v} + 2\overset{\rightharpoonup}{u}$$
$$3\left(-2 \hat{i} + 7 \hat{j}\right) + 2\left(\hat{i} - 5 \hat{j}\right)$$
$$-6\hat{i} + 21\hat{j} + 2\hat{i} - 10\hat{j}$$
$$-4\hat{i} + 11\hat{j}$$
Write \(\overset{\rightharpoonup}{w} = 3\hat{i} - 5\hat{j}\) in component form and find \(2\overset{\rightharpoonup}{w}\).
Answer
\(\langle 3, -5 \rangle\); \(6\hat{i} - 10\hat{j}\)
$$\overset{\rightharpoonup}{v} = \langle v_x, v_y \rangle = \langle q_x - p_x, q_y - p_y \rangle$$
where \(\left(p_x, p_y\right)\) is the initial point and \(\left(q_x, q_y\right)\) is the terminal point.
Magnitude
$$\lVert \overset{\rightharpoonup}{v} \rVert = \sqrt{\left(q_x - p_x\right)^2 + \left(q_y - p_y\right)^2} = \sqrt{v_x^2 + v_y^2}$$
Graphically
Algebraically
Graphically
Algebraically
Let \(\overset{\rightharpoonup}{u}\), \(\overset{\rightharpoonup}{v}\), and \(\overset{\rightharpoonup}{w}\) be vectors and let a and b be scalars.
A unit vector in the direction of \(\overset{\rightharpoonup}{v}\)
$$\hat{u} = \frac{\overset{\rightharpoonup}{v}}{\lVert \overset{\rightharpoonup}{v} \rVert}$$
\(\hat{i} = \langle 1, 0 \rangle\) and signifies the x-component
\(\hat{j} = \langle 0, 1 \rangle\) and signifies the y-component
$$\langle v_x, v_y \rangle = v_x \hat{i} + v_y \hat{j}$$
Helpful videos about this lesson.
