Precalculus by Richard Wright

Previous Lesson Table of Contents Next Lesson

Are you not my student and
has this helped you?

This book is available
to download as an epub.


Suppose a brother or a sister is without clothes and daily food. If one of you says to them, “Go in peace; keep warm and well fed,” but does nothing about their physical needs, what good is it? James 2:15-16 NIV

6-04 Write Vectors in Trigonometric Form

Mr. Wright teaches the lesson.

Summary: In this section, you will:

SDA NAD Content Standards (2018): PC.5.3, PC.6.4

Airplane
Airplane with vectors. (wikimedia commons/Beata (modified))

Lesson 6-03 showed that vectors can be useful to describe quantities that have direction. That direction was described in components: the horizontal measure and vertical measure. A formula had to be used to the get the total magnitude. Sometimes it is more convenient to describe the vector by the magnitude and direction angle. The direction angle is the angle the vector is pointing.

Direction Angle

Vector with components and magnitude and direction angle.

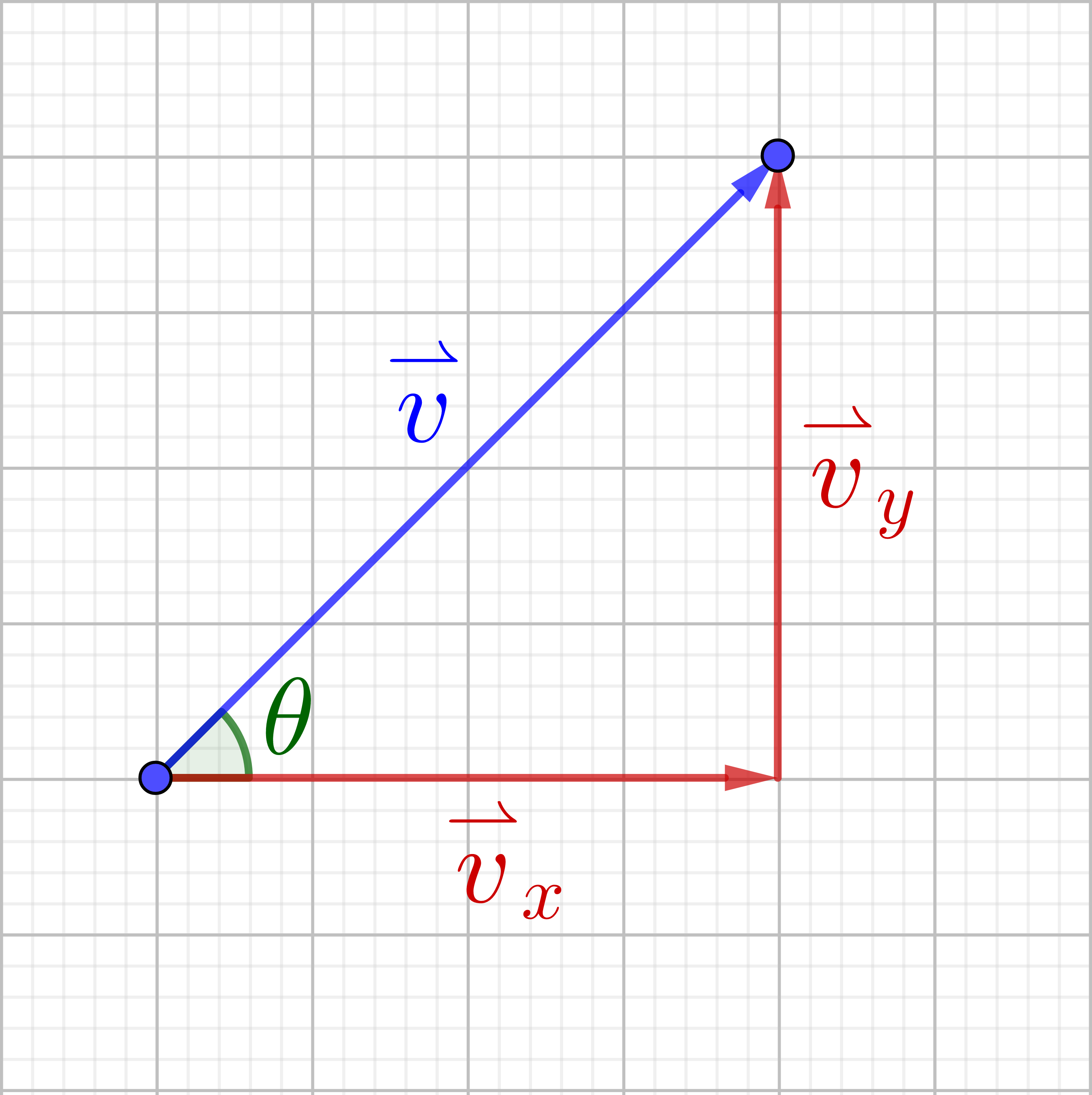
The vector and its components form a right triangle. Using trigonometry the following relationships are revealed.

$$v_x = \lVert \overset{\rightharpoonup}{v} \rVert \cos θ$$

$$v_y = \lVert \overset{\rightharpoonup}{v} \rVert \sin θ$$

 

$$\lVert \overset{\rightharpoonup}{v} \rVert = \sqrt{v_x^2 + v_y^2}$$

$$\tan θ = \frac{v_y}{v_x}$$

Vector \(\overset{\rightharpoonup}{v}\) can be written in trigonometric form as

$$\overset{\rightharpoonup}{v} = \lVert \overset{\rightharpoonup}{v} \rVert \langle \cos θ, \sin θ \rangle$$

Vectors in Trigonometric Form

$$\overset{\rightharpoonup}{v} = \lVert \overset{\rightharpoonup}{v} \rVert \langle \cos θ, \sin θ \rangle$$

Where

$$v_x = \lVert \overset{\rightharpoonup}{v} \rVert \cos θ$$

$$v_y = \lVert \overset{\rightharpoonup}{v} \rVert \sin θ$$

And

$$\lVert \overset{\rightharpoonup}{v} \rVert = \sqrt{v_x^2 + v_y^2}$$

$$\tan θ = \frac{v_y}{v_x}$$

Convert Between Component Form and Trigonometric Form

  1. Write \(\overset{\rightharpoonup}{m} = \langle -12, 5 \rangle\) in trigonometric form.
  2. Write \(\overset{\rightharpoonup}{n} = 6 \langle \cos 225°, \sin 225° \rangle\) in component form.

Solution

  1. Find the magnitude.

    $$\lVert \overset{\rightharpoonup}{m} \rVert = \sqrt{m_x^2 + m_y^2}$$

    $$= \sqrt{\left(-12\right)^2 + 5^2}$$

    $$= 13$$

    Find the angle.

    $$\tan θ = \frac{5}{-12}$$

    $$θ ≈ -30.3°$$

    But this is in the wrong quadrant, so \(θ = -30.3° + 180° = 149.7°\).

    $$\overset{\rightharpoonup}{m} = 13 \langle \cos 149.7°, \sin 149.7° \rangle$$

  2. Evaluate the trigonometric functions.

    $$\overset{\rightharpoonup}{n} = 6 \langle -\frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2} \rangle$$

    Now distribute the magnitude.

    $$\overset{\rightharpoonup}{n} = \langle -3\sqrt{2}, -3\sqrt{2} \rangle$$

Write a Vector in Trigonometric Form

A hang-glider is diving at 20 mph at 30° below the horizontal. (a) Write the vector in trigonometric form and (b) write the vector in component form.

Solution

Hang glider

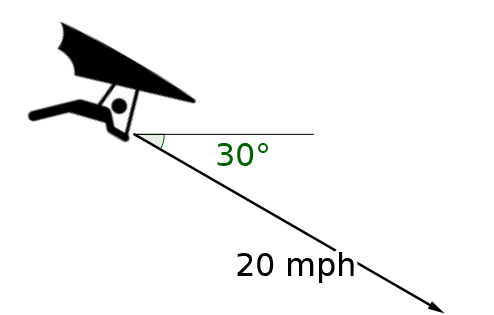
  1. The angle is below the horizontal so the angle is standard position would be 360° – 30° = 330°.

    $$\overset{\rightharpoonup}{v} = \lVert \overset{\rightharpoonup}{v} \rVert \langle \cos θ, \sin θ \rangle$$

    $$= 20 \langle \cos 330°, \sin 330°\rangle$$

  2. Multiply and evaluate the trigonometric form to get component form.

    $$\overset{\rightharpoonup}{v} = 20 \langle \frac{\sqrt{3}}{2}, -\frac{1}{2} \rangle$$

    $$= \langle 10\sqrt{3}, -10 \rangle$$

(a) Write \(\overset{\rightharpoonup}{x}\) = 23 m at N 15° W in trigonometric form, and (b) write \(8\langle \cos 45°, \sin 45° \rangle\) in component form.

Answers

\(23\langle \cos 105°, \sin 105° \rangle\); \(\langle 4\sqrt{2}, 4\sqrt{2} \rangle\)

Add Vectors in Trigonometric Form

To add vectors in trigonometric form, it is easiest to first find the component form and then add the vectors as in lesson 6-03.

Adding Vectors in Trigonometric Form
  1. Write the vectors in component form using \(v_x = \lVert \overset{\rightharpoonup}{v} \rVert \cos θ\) and \(v_y = \lVert \overset{\rightharpoonup}{v} \rVert \sin θ\).
  2. Add the corresponding components.
  3. Put the resultant in trigonometric form using \(\lVert \overset{\rightharpoonup}{v} \rVert = \sqrt{v_x^2 + v_y^2}\) and \(\tan θ = \frac{v_y}{v_x}\).

Add Vectors in Trigonometric Form

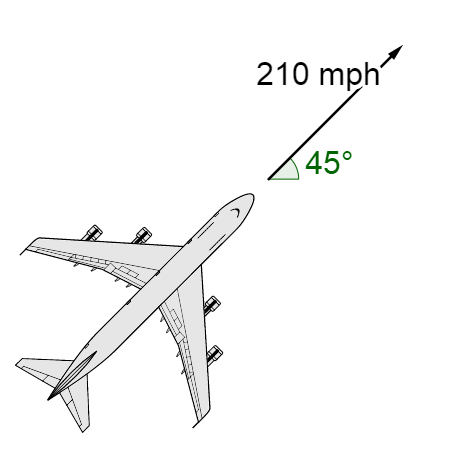
An airplane is traveling at 250 mph at S 45° E and the wind is blowing at 30 mph at W 30° N. What is the airplane’s actually speed and direction?

Solution

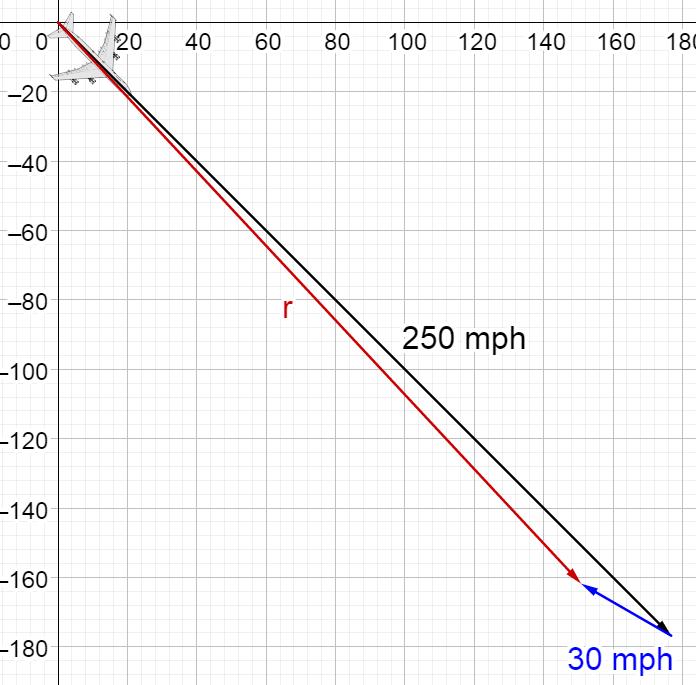
Airplane vector, wind vector, resultant vector (r).

The actually speed and direction of airplane will the the plane’s velocity plus the wind’s velocity. Start by writing both velocities as vectors in trigonometric form.

The angle of \(\overset{\rightharpoonup}{p}\) in standard position is 315°. The angle \(\overset{\rightharpoonup}{w}\) in standard position is 150°.

$$\overset{\rightharpoonup}{p} = \lVert \overset{\rightharpoonup}{p} \rVert \langle \cos θ, \sin θ \rangle$$

$$\overset{\rightharpoonup}{p} = 250 \langle \cos 315°, \sin 315° \rangle$$

$$\overset{\rightharpoonup}{w} = 30 \langle \cos 150°, \sin 150° \rangle$$

Now, put the vectors in component form by evaluating and multiplying.

$$\overset{\rightharpoonup}{p} = 250 \langle \frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2} \rangle$$

$$= \langle 125\sqrt{2}, -125\sqrt{2} \rangle$$


$$\overset{\rightharpoonup}{w} = 30 \langle -\frac{\sqrt{3}}{2}, \frac{1}{2} \rangle$$

$$= \langle -15\sqrt{3}, 15 \rangle$$

Add the vectors together.

$$\overset{\rightharpoonup}{r} = \overset{\rightharpoonup}{p} + \overset{\rightharpoonup}{w}$$

$$= \langle 125\sqrt{2}, -125\sqrt{2} \rangle + \langle -15\sqrt{3}, 15 \rangle$$

$$= \langle 125\sqrt{2} - 15\sqrt{3}, -125\sqrt{2} + 15 \rangle$$

$$= \langle 150.8, -161.8 \rangle$$

Now, convert the resultant to trigonometric form.

$$\lVert \overset{\rightharpoonup}{r} \lVert = \sqrt{r_x^2 + r_y^2}$$

$$= \sqrt{150.8^2 + \left(-161.8\right)^2}$$

$$≈ 221.2$$

$$\tan θ = \frac{r_y}{r_x}$$

$$\tan θ = \frac{-161.8}{150.8}$$

$$θ ≈ -47.0° + 360° = 313.0°$$

The 360° is added to put the angle in standard form.

$$\overset{\rightharpoonup}{r} = 221.2 \langle \cos 313.0°, \sin 313.0° \rangle$$

The airplane’s actual speed and direction is 221.2 mph at E 47.0° S.

Add \(\overset{\rightharpoonup}{a}\) = 23 m at S 25° E and \(\overset{\rightharpoonup}{b}\) = 12 m at E 17° N.

Answer

27.38 m at E 39.28° S

Lesson Summary
Vectors in Trigonometric Form

$$\overset{\rightharpoonup}{v} = \lVert \overset{\rightharpoonup}{v} \rVert \langle \cos θ, \sin θ \rangle$$

Where

$$v_x = \lVert \overset{\rightharpoonup}{v} \rVert \cos θ$$

$$v_y = \lVert \overset{\rightharpoonup}{v} \rVert \sin θ$$

And

$$\lVert \overset{\rightharpoonup}{v} \rVert = \sqrt{v_x^2 + v_y^2}$$

$$\tan θ = \frac{v_y}{v_x}$$

Adding Vectors in Trigonometric Form
  1. Write the vectors in component form using \(v_x = \lVert \overset{\rightharpoonup}{v} \rVert \cos θ\) and \(v_y = \lVert \overset{\rightharpoonup}{v} \rVert \sin θ\).
  2. Add the corresponding components.
  3. Put the resultant in trigonometric form using \(\lVert \overset{\rightharpoonup}{v} \rVert = \sqrt{v_x^2 + v_y^2}\) and \(\tan θ = \frac{v_y}{v_x}\).

Helpful videos about this lesson.

Practice Exercises

  1. How do you convert a vector in component form into trigonometric form?
  2. Write the following vectors in trigonometric form.
  3. ⟨4, 3⟩
  4. ⟨24, −7⟩
  5. ⟨−6, 8⟩
  6. 25 ft at S 25° W
  7. Write the following vectors in component form.
  8. 18⟨cos 60°, sin 60°⟩
  9. 12⟨cos 315°, sin 315°⟩
  10. 24⟨cos 120°, sin 120°⟩
  11. 40 m at N 30° E
  12. Add the following pairs of vectors. Write the result in trigonometric form.
  13. 4⟨cos 45°, sin 45°⟩ + 12⟨cos 135°, sin 135°⟩
  14. 10⟨cos 240°, sin 240°⟩ + 16⟨cos 60°, sin 60°⟩
  15. (4 km/h at N 15° E) + (6 km/h at N 30° E)
  16. (14 m/s at E 40° S) + (11 m/s at S 10° W)
  17. Problem Solving
  18. A boat leaves the pier and travels 20 miles due west. Then it turns and sails 15 miles at N 20° W. What is the boat’s final distance and direction from the pier?
  19. A hiker in the woods hikes 3 miles at N 30° E, then turns and hikes 2.5 miles at E 10° N. Where is the hiker from his starting point?
  20. Mixed Review
  21. (6-03) Given \(\overset{\rightharpoonup}{u} = \langle 2, -1 \rangle\) and \(\overset{\rightharpoonup}{v} = \langle 0, 4 \rangle\), evaluate \(\overset{\rightharpoonup}{u} - 2\overset{\rightharpoonup}{v}\) (a) graphically and (b) algebraically.
  22. (6-03) Find a unit vector in the direction of \(\overset{\rightharpoonup}{w} = \langle -2, 3 \rangle\).
  23. (6-02) Find the area of ΔABC where a = 2, b = 5, and c = 4.
  24. (6-01) How many solutions are there for ∆VWX where X = 20°, w = 40, x = 25?
  25. (4-02) Evaluate all six trigonometric functions for the angle \(\frac{7π}{6}\) using the unit circle.

Answers

  1. Find r with \(\sqrt{v_x^2 + v_y^2}\) and the angle with \(\tan θ = \frac{v_y}{v_x}\).
  2. 5⟨cos 36.9°, sin 36.9°⟩
  3. 25⟨cos 343.7°, sin 343.7°⟩
  4. 10⟨cos 126.9°, sin 126.9°⟩
  5. 25⟨cos 245°, sin 245°⟩
  6. \(\langle 9, 9\sqrt{3}\rangle\)
  7. \(\langle 6\sqrt{2}, -6\sqrt{2}\rangle\)
  8. \(\langle -12, 12\sqrt{3}\rangle\)
  9. \(\langle 20, 20\sqrt{3}\rangle\)
  10. \(4\sqrt{10} \langle \cos 116.6°, \sin 116.6° \rangle\)
  11. 6⟨cos 60°, sin 60°⟩
  12. 9.92⟨cos 66.0°, sin 66.0°⟩
  13. 21.7⟨cos 294.0°, sin 294.0°⟩
  14. 28.8 miles at W 29.3° N
  15. 4.99 miles at E 37.4° N
  16. ; ⟨2, −9⟩
  17. \(\left\langle \frac{-2\sqrt{13}}{13}, \frac{3\sqrt{13}}{13} \right\rangle\)
  18. 3.8
  19. 2 solutions
  20. \(\sin \frac{7π}{6} = -\frac{1}{2}\), \(\cos \frac{7π}{6} = -\frac{\sqrt{3}}{2}\), \(\tan \frac{7π}{6} = \frac{\sqrt{3}}{3}\), \(\csc \frac{7π}{6} = -2\), \(\sec \frac{7π}{6} = -\frac{2\sqrt{3}}{3}\), \(\cot \frac{7π}{6} = \sqrt{3}\)