Precalculus by Richard Wright
Precalculus by Richard Wright
For God has not given us a spirit of fear, but of power and of love and of a sound mind. 2 Timothy 1:7 NKJV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.6.4

In physics, work is found by multiplying force and the distance the force moves an object. However, the force and distance need to be in the same direction. The easiest way to calculate this is by describing both the force and distance as vectors and finding the dot product.
There are two ways to multiply vectors, the dot product and the cross product. The dot product of two vectors is sometimes called the scalar product because the result is a scalar number. The dot product of two vectors \(\overset{\rightharpoonup}{u} = \langle u_x, u_y \rangle\) and \(\overset{\rightharpoonup}{v} = \langle v_x, v_y \rangle\) is \(\overset{\rightharpoonup}{u} \cdot \overset{\rightharpoonup}{v} = u_x v_x + u_y v_y\).
Let \(\overset{\rightharpoonup}{u} = \langle u_x, u_y \rangle\) and \(\overset{\rightharpoonup}{v} = \langle v_x, v_y \rangle\), then
$$\overset{\rightharpoonup}{u} \cdot \overset{\rightharpoonup}{v} = u_x v_x + u_y v_y$$
If \(\overset{\rightharpoonup}{u}\), \(\overset{\rightharpoonup}{v}\), and \(\overset{\rightharpoonup}{w}\) are vectors and a is a scalar, then
Find the dot product of ⟨2, −1⟩ · ⟨7, 3⟩.
Solution
$$\overset{\rightharpoonup}{u} \cdot \overset{\rightharpoonup}{v} = u_x v_x + u_y v_y$$
⟨2, −1⟩ · ⟨7, 3⟩ = 2(7) + −1(3)
= 11
Find the dot product of ⟨2, 9⟩ · ⟨10, −1⟩.
Answer
11
An alternate way of evaluating the dot product is \(\overset{\rightharpoonup}{u} \cdot \overset{\rightharpoonup}{v} = \lVert \overset{\rightharpoonup}{u} \rVert \lVert \overset{\rightharpoonup}{v} \rVert \cos θ\) where θ is the angle between the vectors. This can be used to find the dot product when the magnitudes and angle are known, or it can be used to find the angle between the vectors.
If \(\overset{\rightharpoonup}{u}\) and \(\overset{\rightharpoonup}{v}\) are vectors, then
$$\overset{\rightharpoonup}{u} \cdot \overset{\rightharpoonup}{v} = \lVert \overset{\rightharpoonup}{u} \rVert \lVert \overset{\rightharpoonup}{v} \rVert \cos θ$$
Find the angle between ⟨2, −1⟩ and ⟨7, 3⟩.
Solution
$$\overset{\rightharpoonup}{u} \cdot \overset{\rightharpoonup}{v} = \lVert \overset{\rightharpoonup}{u} \rVert \lVert \overset{\rightharpoonup}{v} \rVert \cos θ$$
$$\langle 2, -1 \rangle \cdot \langle 7, 3 \rangle = \lVert \langle 2, -1 \rangle\ \rVert \lVert \langle 7, 3 \rangle \rVert \cos θ$$
$$2\left(7\right) + -1\left(3\right) = \sqrt{2^2 + \left(-1\right)^2} \sqrt{7^2 + 3^2} \cos θ$$
$$11 = \sqrt{5} \sqrt{58} \cos θ$$
0.6459422415 = cos θ
θ ≈ 49.8°
Find the angle between ⟨−3, 4⟩ and ⟨12, −5⟩.
Answer
149.5°
Notice in this form, the dot product depends on cosine. If θ = 90°, then cos θ = 0. Thus, if the dot product is zero, the vectors are orthogonal or at 90° to each other.
If \(\overset{\rightharpoonup}{u} \cdot \overset{\rightharpoonup}{v} = 0\), then \(\overset{\rightharpoonup}{u}\) and \(\overset{\rightharpoonup}{v}\) are orthogonal.
If \(\overset{\rightharpoonup}{u} = k\overset{\rightharpoonup}{v}\), then \(\overset{\rightharpoonup}{u}\) and \(\overset{\rightharpoonup}{v}\) are parallel.
Are the vectors ⟨3, 6⟩ and ⟨−4, 2⟩ parallel, orthogonal, or neither?
Solution
$$\overset{\rightharpoonup}{u} \cdot \overset{\rightharpoonup}{v}$$
= ⟨3, 6⟩ · ⟨−4, 2⟩
= 3(−4) + 6(2)
= 0
Because \(\overset{\rightharpoonup}{u} \cdot \overset{\rightharpoonup}{v} = 0\), the vectors are orthogonal.
Are the vectors ⟨12, −18⟩ and ⟨−8, 12⟩ orthogonal, parallel, or neither?
Answer
Parallel
Sometimes it is useful to be able to write a vector in components that are not simply horizontal and vertical. Vector components are two orthogonal vectors that add to produce the original vector. An example is forces and work on an incline where it is most convenient to have one component parallel to the incline and the other component orthogonal to the incline.
To find orthogonal components of a vector \(\overset{\rightharpoonup}{u}\), you need to find two vectors \(\overset{\rightharpoonup}{w_1}\) and \(\overset{\rightharpoonup}{w_2}\) such that \(\overset{\rightharpoonup}{u} = \overset{\rightharpoonup}{w_1} + \overset{\rightharpoonup}{w_2}\) where \(\overset{\rightharpoonup}{w_1}\) is in the direction of \(\overset{\rightharpoonup}{v}\). \(\overset{\rightharpoonup}{w_1} = \text{proj}_\overset{\rightharpoonup}{v} \overset{\rightharpoonup}{u}\) and \(\overset{\rightharpoonup}{w_2} = \overset{\rightharpoonup}{u} - \overset{\rightharpoonup}{w_1}\).
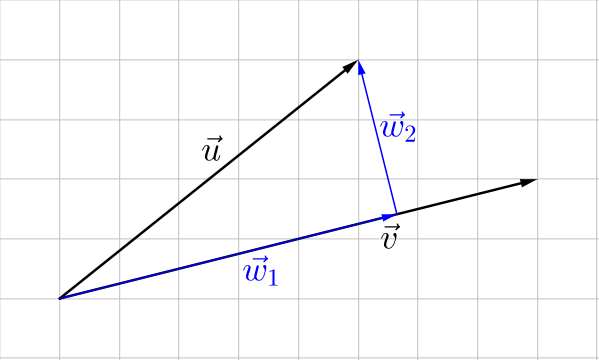
Find the orthogonal components of \(\overset{\rightharpoonup}{u}\) where one component is in the direction of \(\overset{\rightharpoonup}{v}\).
The vector projection is \(\overset{\rightharpoonup}{u} \cdot \overset{\rightharpoonup}{v} = \lVert \overset{\rightharpoonup}{u} \rVert \lVert \overset{\rightharpoonup}{v} \rVert \cos θ\) solved for \(\lVert \overset{\rightharpoonup}{u} \rVert \cos θ = \frac{\overset{\rightharpoonup}{u} \cdot \overset{\rightharpoonup}{v}}{\lVert \overset{\rightharpoonup}{v} \rVert}\). This gives the length of \(\overset{\rightharpoonup}{u}\) which covers \(\overset{\rightharpoonup}{v}\). This is multiplied by the unit vector in the direction of \(\overset{\rightharpoonup}{v}\) which is \(\frac{\overset{\rightharpoonup}{v}}{\lVert \overset{\rightharpoonup}{v} \rVert}\) to give a direction to the length.
$$\text{proj}_\overset{\rightharpoonup}{v} \overset{\rightharpoonup}{u} = \frac{\overset{\rightharpoonup}{u} \cdot \overset{\rightharpoonup}{v}}{\lVert \overset{\rightharpoonup}{v} \rVert} \frac{\overset{\rightharpoonup}{v}}{\lVert \overset{\rightharpoonup}{v} \rVert}$$
$$\text{proj}_\overset{\rightharpoonup}{v} \overset{\rightharpoonup}{u} = \frac{\overset{\rightharpoonup}{u} \cdot \overset{\rightharpoonup}{v}}{\lVert \overset{\rightharpoonup}{v} \rVert^2} \overset{\rightharpoonup}{v}$$
The projection of \(\overset{\rightharpoonup}{u}\) onto \(\overset{\rightharpoonup}{v}\) is
$$\text{proj}_\overset{\rightharpoonup}{v} \overset{\rightharpoonup}{u} = \frac{\overset{\rightharpoonup}{u} \cdot \overset{\rightharpoonup}{v}}{\lVert \overset{\rightharpoonup}{v} \rVert^2} \overset{\rightharpoonup}{v}$$
Find orthogonal components of \(\overset{\rightharpoonup}{u} = \langle 2, 3 \rangle \) where one component is orthogonal to \(\overset{\rightharpoonup}{v} = \langle 5, 4 \rangle \).
Solution
The first component is the projection of \(\overset{\rightharpoonup}{u}\) onto \(\overset{\rightharpoonup}{v}\).
$$\overset{\rightharpoonup}{w_1} = \text{proj}_\overset{\rightharpoonup}{v} \overset{\rightharpoonup}{u}$$
$$= \frac{\overset{\rightharpoonup}{u} \cdot \overset{\rightharpoonup}{v}}{\lVert \overset{\rightharpoonup}{v} \rVert^2} \overset{\rightharpoonup}{v}$$
$$= \frac{\langle 2, 3 \rangle \cdot \langle 5, 4 \rangle}{\lVert \langle 5, 4 \rangle \rVert^2} \langle 5, 4 \rangle$$
$$= \frac{2\left(5\right) + 3\left(4\right)}{\sqrt{5^2 + 4^2}^2} \langle 5, 4 \rangle$$
$$= \frac{22}{41} \langle 5, 4 \rangle$$
$$= \left\langle \frac{110}{41}, \frac{88}{41} \right\rangle$$
The second component is found by subtracting the \(\overset{\rightharpoonup}{w_1}\) from \(\overset{\rightharpoonup}{u}\).
$$\overset{\rightharpoonup}{w_2} = \overset{\rightharpoonup}{u} - \overset{\rightharpoonup}{w_1}$$
$$= \langle 2, 3 \rangle - \left\langle \frac{110}{41}, \frac{88}{41} \right\rangle$$
$$= \left\langle -\frac{28}{41}, \frac{35}{41} \right\rangle$$
Find orthogonal components of \(\overset{\rightharpoonup}{u} = \langle -4, 1 \rangle\) where one component is orthogonal to \(\overset{\rightharpoonup}{v} = \langle -5, 2 \rangle\).
Answer
\(\overset{\rightharpoonup}{w_1} = \left\langle -\frac{110}{29}, \frac{44}{29} \right\rangle\), \(\overset{\rightharpoonup}{w_2} = \left\langle -\frac{6}{29}, -\frac{15}{29} \right\rangle\)
Let \(\overset{\rightharpoonup}{u} = \langle u_x, u_y \rangle\) and \(\overset{\rightharpoonup}{v} = \langle v_x, v_y \rangle\), then
$$\overset{\rightharpoonup}{u} \cdot \overset{\rightharpoonup}{v} = u_x v_x + u_y v_y$$
If \(\overset{\rightharpoonup}{u}\), \(\overset{\rightharpoonup}{v}\), and \(\overset{\rightharpoonup}{w}\) are vectors and a is a scalar, then
If \(\overset{\rightharpoonup}{u}\) and \(\overset{\rightharpoonup}{v}\) are vectors, then
$$\overset{\rightharpoonup}{u} \cdot \overset{\rightharpoonup}{v} = \lVert \overset{\rightharpoonup}{u} \rVert \lVert \overset{\rightharpoonup}{v} \rVert \cos θ$$
If \(\overset{\rightharpoonup}{u} \cdot \overset{\rightharpoonup}{v} = 0\), then \(\overset{\rightharpoonup}{u}\) and \(\overset{\rightharpoonup}{v}\) are orthogonal.
If \(\overset{\rightharpoonup}{u} = k\overset{\rightharpoonup}{v}\), then \(\overset{\rightharpoonup}{u}\) and \(\overset{\rightharpoonup}{v}\) are parallel.
Find the orthogonal components of \(\overset{\rightharpoonup}{u}\) where one component is in the direction of \(\overset{\rightharpoonup}{v}\).
The projection of \(\overset{\rightharpoonup}{u}\) onto \(\overset{\rightharpoonup}{v}\) is
$$\text{proj}_\overset{\rightharpoonup}{v} \overset{\rightharpoonup}{u} = \frac{\overset{\rightharpoonup}{u} \cdot \overset{\rightharpoonup}{v}}{\lVert \overset{\rightharpoonup}{v} \rVert^2} \overset{\rightharpoonup}{v}$$
Helpful videos about this lesson.