Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
The way of the sluggard is blocked with thorns, but the path of the upright is a highway. Proverbs 15:19 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.5.6
Complex numbers are mathematically interesting, but can be used to solve real-world problems such as in electrical engineering to find how different electrical components effect electrical current.
Complex numbers were introduced in lesson 2-01 as solutions to polynomial equations. Recall that the complex unit is \(i = \sqrt{-1}\) and that complex numbers are written in the form a + bi.
To graph complex numbers, a rectangular coordinate system is used with the horizontal axis for the real part and the vertical axis for the imaginary part. Numbers are graphed by finding the point with the real and imaginary parts. For example, the points 2 + 3i and −1 + 2i.
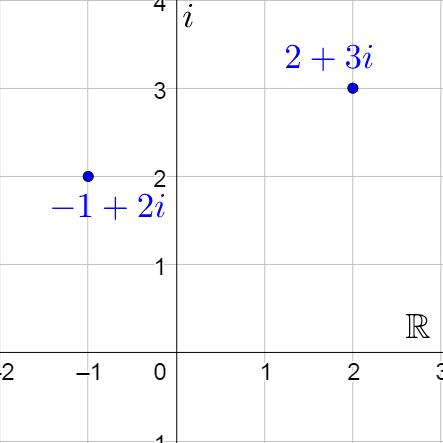
The complex plane has the real axis as the horizontal and the imaginary axis as vertical.
Plot a number by finding the point with the specified real and imaginary parts.
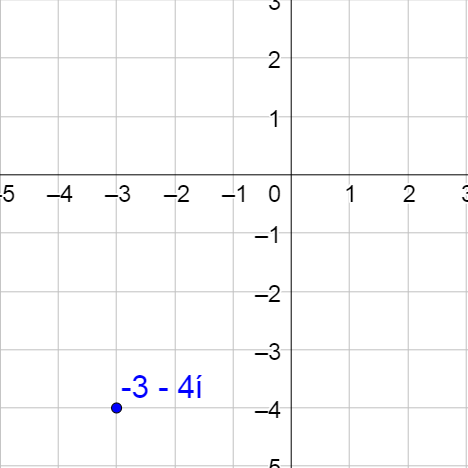
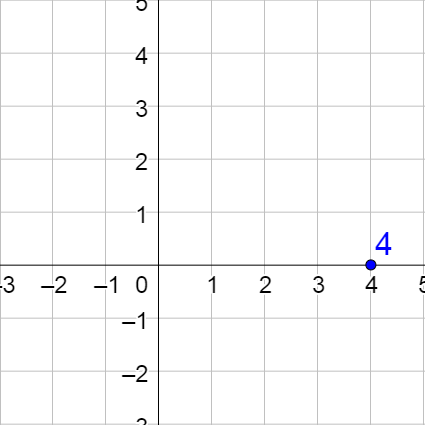
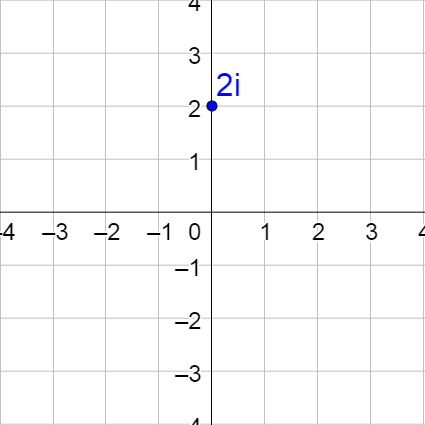
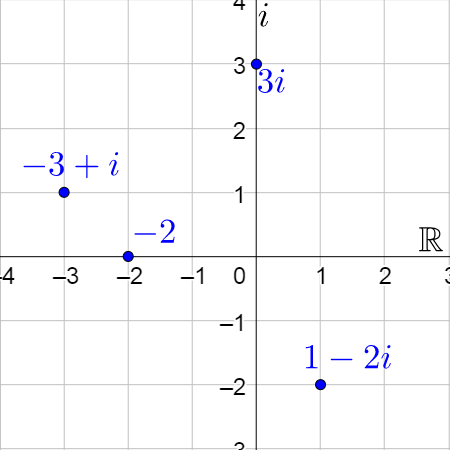
Graph the complex numbers 1 – 2i, −3 + i, −2, and 3i.
Solution
Move the distance of the real number to the right and then up the imaginary part.
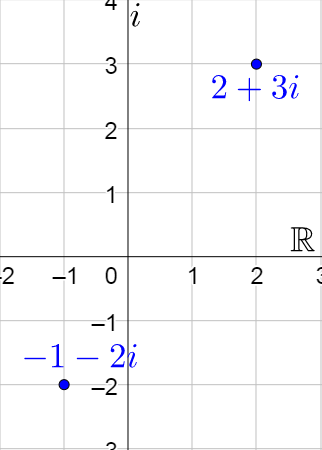
Graph 2 + 3i and −1 − 2i.
Answer
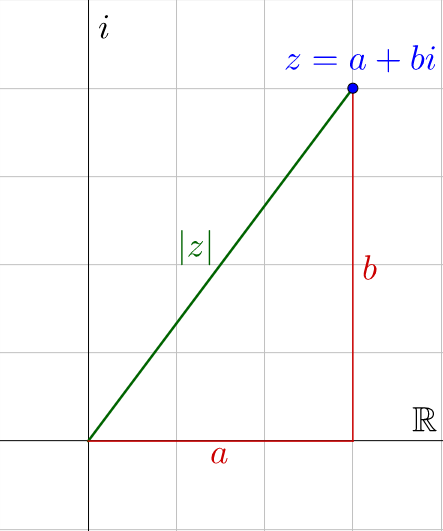
Absolute value is defined as the distance a number is from 0. For complex numbers the distance formula needs to be used.
$$\lvert a + bi \rvert = \sqrt{a^2 + b^2}$$
Notice that i is not used to find the absolute value because the distance formula uses the horizontal and vertical distances, in this case a and b.
$$\lvert a + bi \rvert = \sqrt{a^2 + b^2}$$
Find the absolute value of (a) 1 – 2i and (b) 3 + i.
Solution
$$\lvert a + bi \rvert = \sqrt{a^2 + b^2}$$
$$\lvert 1 - 2i \rvert = \sqrt{1^2 + \left(-1\right)^2}$$
$$= \sqrt{5}$$
$$\lvert a + bi \rvert = \sqrt{a^2 + b^2}$$
$$\lvert 3 + i \rvert = \sqrt{3^2 + 1^2}$$
$$= \sqrt{10}$$
Find the absolute value of 4 − 3i.
Answer
5
Another way to graph a complex number is by the distance from the origin and the angle in standard position.
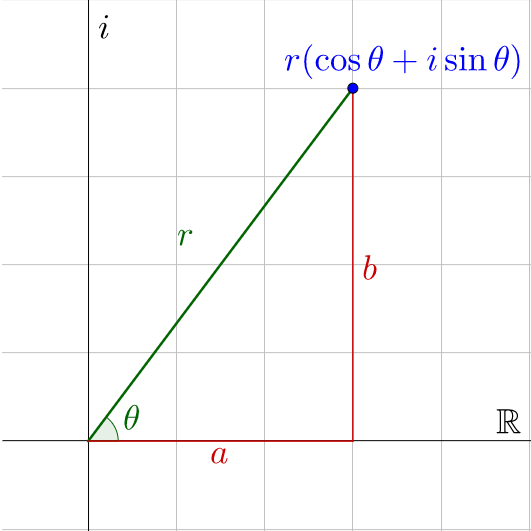
From the graph, a = r cos θ and b = r sin θ.
z = a + bi
z = r cos θ + ir sin θ
z = r(cos θ + i sin θ)
This is called the trigonometric form or polar form.
Also from the graph \(r = \sqrt{a^2 + b^2}\) and \(\tan θ = \frac{b}{a}\).
z = r(cos θ + i sin θ)
r is called the modulus and θ is called the argument
Convert between trigonometric form and standard form using
a = r cos θ
b = r sin θ
$$r = \sqrt{a^2 + b^2}$$
$$\tan θ = \frac{b}{a}$$
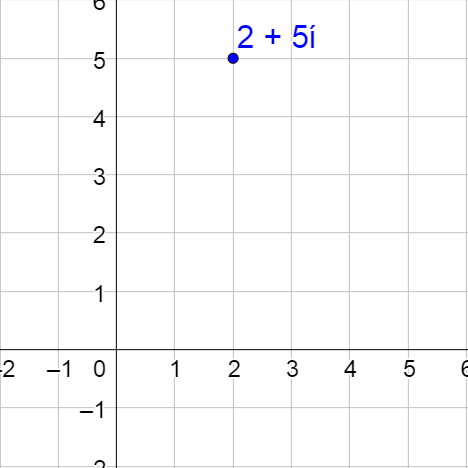
Write (a) −2 + 5i and (b) 12 – 5i in trigonometric form.
Solution
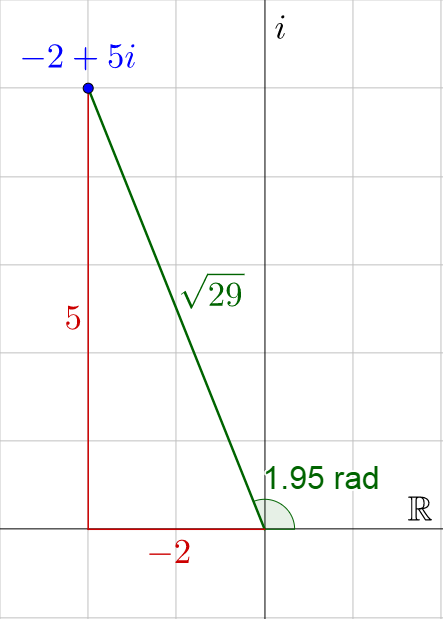
Start by finding r.
$$r = \sqrt{a^2 + b^2}$$
$$= \sqrt{\left(-2\right)^2 + 5^2}$$
$$= \sqrt{29}$$
Now find θ.
$$\tan θ = \frac{b}{a}$$
$$\tan θ = \frac{5}{-2}$$
$$θ ≈ -1.1903 + π$$
$$θ ≈ 1.95$$
The π was added to put the angle in the correct quadrant. Now write the number.
$$z = \sqrt{29}\left(\cos 1.95 + i \sin 1.95\right)$$
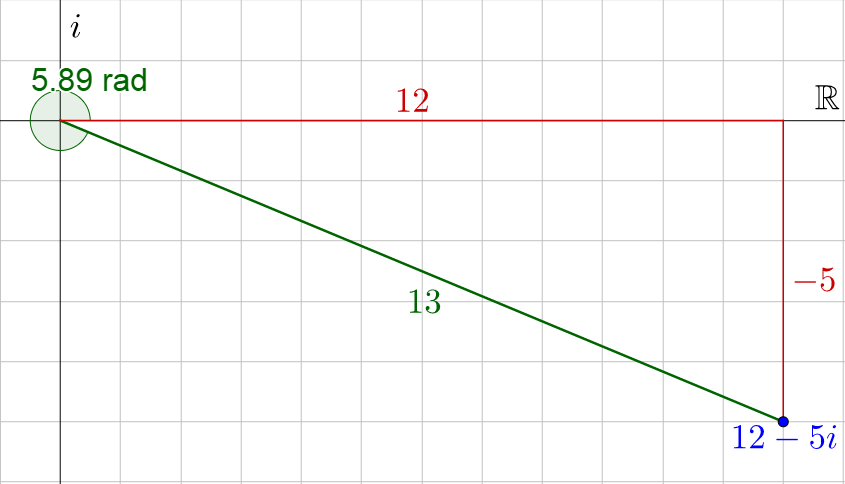
Start by finding r.
$$r = \sqrt{a^2 + b^2}$$
$$= \sqrt{12^2 + \left(-5\right)^2}$$
$$= 13$$
Now find θ.
$$\tan θ = \frac{b}{a}$$
$$\tan θ = \frac{-5}{12}$$
$$θ = -0.3948 + 2π$$
$$θ = 5.8884$$
The 2π was added to make the angle positive. Now write the number.
$$z = 13\left(\cos 5.89 + i \sin 5.89\right)$$
Write 4 − 4i in trigonometric form.
Answer
\(4\sqrt{2}\left(\cos \frac{7π}{4} + i \sin \frac{7π}{4}\right)\)
Write (a) \(4\left(\cos \frac{2π}{3} + i \sin \frac{2π}{3}\right)\) and (b) \(10\left(\cos \frac{π}{4} + i \sin \frac{π}{4}\right)\) in standard form.
Solution
Evaluate the trigonometric expressions.
$$4\left(\cos \frac{2π}{3} + i \sin \frac{2π}{3}\right)$$
$$4\left(-\frac{1}{2} + i \frac{\sqrt{3}}{2}\right)$$
Now distribute the 4.
$$-2 + 2\sqrt{3} i$$
Evaluate the trigonometric expressions.
$$10\left(\cos \frac{π}{4} + i \sin \frac{π}{4}\right)$$
$$10\left(\frac{\sqrt{2}}{2} + i \frac{\sqrt{3}}{2}\right)$$
Now distribute the 10.
$$5\sqrt{2} + 5\sqrt{2} i$$
Write \(16\left(\cos \frac{11π}{6} + i \sin \frac{11π}{6}\right)\) in standard form.
Answer
\(8\sqrt{3} - 8i\)
The complex plane has the real axis as the horizontal and the imaginary axis as vertical.
Plot a number by finding the point with the specified real and imaginary parts.
$$\lvert a + bi \rvert = \sqrt{a^2 + b^2}$$
z = r(cos θ + i sin θ)
r is called the modulus and θ is called the argument
Convert between trigonometric form and standard form using
a = r cos θ
b = r sin θ
$$r = \sqrt{a^2 + b^2}$$
$$\tan θ = \frac{b}{a}$$
Helpful videos about this lesson.
