Precalculus by Richard Wright

Previous Lesson Table of Contents Next Lesson

Are you not my student and
has this helped you?

This book is available
to download as an epub.


Jesus answered, “I am the way and the truth and the life. No one comes to the Father except through me.” John 14:6 NIV

6-07 Trigonometric Form of a Complex Number: Operations

Mr. Wright teaches the lesson.

Summary: In this section, you will:

SDA NAD Content Standards (2018): PC.5.6

Children in circle
Children in a circle during VBS. (Holloman Air Force Base/Airman Leah Ferrante)

Suppose you need to describe locations to completely and evenly encircle something. Let’s say you have exactly five people and you want to have them spaced evenly around a circle with radius of 2. You could describe these points in the complex plane as \(\sqrt[5]{32}\). We will look at this later in the lesson, but first let’s look at other operations with complex numbers.

Multiplication

In standard form (a + bi), multiplying complex numbers involved using the distributive property and changing i2 into −1.

(2 + i)(3 − 2i)

6 − 4i + 3i − 2i2

6 − 4i + 3i + 2

8 − i

However, having the complex numbers in trigonometric form (r(cos θ + i sin θ)) makes the multiplication much easier. Simply multiply the r’s and add the angles.

Multiply Complex Numbers in Trigonometric Form

Let z1 = r1(cos θ1 + i sin θ1) and z2 = r2(cos θ2 + i sin θ2) be complex numbers.

z1z2 = r1r2(cos(θ1 + θ2) + i sin(θ1 + θ2))

If θ1 + θ2 > 2π, then subtract 2π to get a coterminal angle between 0 and 2π.

Multiply Complex Numbers in Trigonometric Form

If \(z_1 = 3\left(\cos \frac{π}{3} + i \sin \frac{π}{3}\right)\) and \(z_2 = 12\left(\cos \frac{π}{6} + i \sin \frac{π}{6}\right)\), find z1z2.

Solution

$$z_1 z_2 = r_1 r_2\left(\cos \left(θ_1 + θ_2\right) + i \sin \left(θ_1 + θ_2\right)\right)$$

$$= 3 \cdot 12\left(\cos \left(\frac{π}{3} + \frac{π}{6}\right) + i \left(\frac{π}{3} + \frac{π}{6}\right)\right)$$

$$= 36\left(\cos \frac{π}{2} + i \sin \frac{π}{2}\right)$$

If \(z_1 = 2\left(\cos \frac{5π}{6} + i \sin \frac{5π}{6}\right)\) and \(z_2 = 5\left(\cos \frac{π}{2} + i \sin \frac{π}{2}\right)\), find z1z2.

Answer

\(10\left(\cos \frac{4π}{3} + i \sin \frac{4π}{3}\right)\)

Division

In standard form, division involved multiplying the numerator and denominator by the complex conjugate of the denominator.

$$\frac{a + bi}{c + di} = \frac{\left(a + bi\right)\left(c - di\right)}{\left(c + di\right)\left(c - di\right)}$$

In trigonometric form, simply divide the r’s and subtract the angles.

Divide Complex Numbers in Trigonometric Form

Let \(z_1 = r_1\left(\cos θ_1 + i \sin θ_1\right)\) and \(z_2 = r_2\left(\cos θ_2 + i \sin θ_2\right)\) be complex numbers.

$$\frac{z_1}{z_2} = \frac{r_1}{r_2}\left(\cos \left(θ_1 - θ_2\right) + i \sin \left(θ_1 - θ_2\right)\right)$$

If θ1 − θ2 < 0, then add 2π to get a coterminal angle between 0 and 2π.

Divide Complex Numbers in Trigonometric Form

If \(z_1 = 3\left(\cos \frac{π}{3} + i \sin \frac{π}{3}\right)\) and \(z_2 = 12\left(\cos \frac{π}{6} + i \sin \frac{π}{6}\right)\), find \(\frac{z_1}{z_2}\).

Solution

$$\frac{z_1}{z_2} = \frac{r_1}{r_2}\left(\cos \left(θ_1 - θ_2\right) + i \sin \left(θ_1 - θ_2\right)\right)$$

$$= \frac{3}{12}\left(\cos \left(\frac{π}{3} - \frac{π}{6}\right) + i \left(\frac{π}{3} - \frac{π}{6}\right)\right)$$

$$= \frac{1}{4}\left(\cos \frac{π}{6} + i \sin \frac{π}{6}\right)$$

If \(z_1 = 2\left(\cos \frac{5π}{6} + i \sin \frac{5π}{6}\right)\) and \(z_2 = 5\left(\cos \frac{π}{2} + i \sin \frac{π}{2}\right)\), find \(\frac{z_1}{z_2}\).

Answer

\(\frac{2}{5}\left(\cos \frac{π}{3} + i \sin \frac{π}{3}\right)\)

Exponents

The only way to deal with exponents with complex numbers in standard form is repeated multiplication which can be tedious. Exponents in trigonometric form are much simpler. Since the multiplication process is multiplying the r’s and adding the angles, exponents which are repeated multiplication will repeatedly multiply the r’s (or exponent) and repeated add the angles (or multiply).

Exponents on Complex Numbers in Trigonometric Form

Let z = r(cos θ + i sin θ) be a complex number.

zn = rn(cos(nθ) + i sin(nθ))

If nθ > 2π, then subtract 2π to get a coterminal angle between 0 and 2π.

Exponents with Complex Numbers in Trigonometric Form

If \(z = 3\left(\cos \frac{π}{3} + i \sin \frac{π}{3}\right)\), find z4.

Solution

$$z^n = r^n\left(\cos \left(nθ\right) + i \sin \left(nθ\right)\right)$$

$$= 3^4\left(\cos \left(4 \frac{π}{3}\right) + i \sin \left(4 \frac{π}{3}\right)\right)$$

$$= 81\left(\cos \frac{4π}{3} + i \sin \frac{4π}{3}\right)$$

If \(z = 2\left(\cos \frac{π}{6} + i \sin \frac{π}{6}\right)\), find z3.

Answer

\(8\left(\cos \frac{π}{2} + i \sin \frac{π}{2}\right)\)

nth Roots

Roots with complex numbers in standard form has not been previously addressed in this book; however, trigonometric form makes it manageable.

First consider a simple example. You would probably solve this equation this way.

x4 − 16 = 0

x4 = 16

$$x = ± \sqrt[4]{16}$$

x = −2, 2

However, the fundamental theorem of algebra says that there should be 4 solutions not 2. Try solving by factoring.

x4 − 16 = 0

(x2 − 4)(x2 + 4) = 0

(x − 2)(x + 2)(x2 + 4) = 0

x – 2 = 0 x + 2 = 0 x2 + 4 = 0
x = 2 x = −2 x2 = -4
\(x = ±\sqrt{-4}\)
x = −2i, 2i

This gives all four solutions. Notice that if you graph these four solutions on a complex plane, they are evenly spaced around a circle with radius \(\sqrt[4]{16} = 2\).

Graph of 2, 2i, −2, −2i

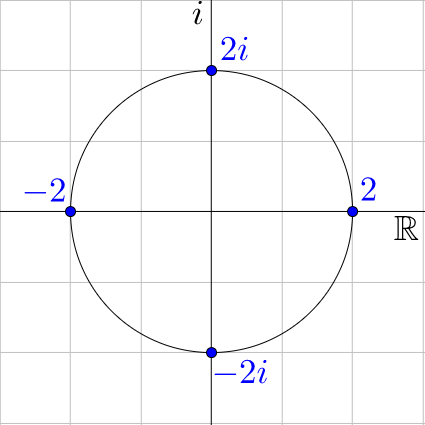
To find these roots for any complex numbers, find the radius of the circle and then the evenly spaced angles around the circle. Exponents had rn and nθ. Roots are the inverse of exponents so the process should be also be the inverses for r and θ.

$$\sqrt[n]{r}\left(\cos \frac{θ}{n} + i \sin \frac{θ}{n}\right)$$

gives the first root.

To get the rest of the roots, divide the circle into n parts and add that to the angle.

Roots of Complex Numbers

Let \(z = r\left(\cos θ + i \sin θ\right)\)

$$\sqrt[n]{z} = \sqrt[n]{r}\left(\cos \left(\frac{θ}{n} + \frac{2πk}{n}\right) + i \sin \left(\frac{θ}{n} + \frac{2πk}{n}\right)\right)$$

Where k = 0, 1, 2, …, n – 1

Find the nth Roots of a Complex Number

Find the cube roots of z = 4 – 4i. Write the answers in standard form.

Solution

First, write the complex number in trigonometric form. Find r.

$$r = \sqrt{a^2 + b^2}$$

$$r = \sqrt{4^2 + \left(-4\right)^2}$$

$$r = 4\sqrt{2}$$

Find θ.

$$\tan θ = \frac{b}{a}$$

$$\tan θ = \frac{-4}{4} = -1$$

$$θ = \frac{7π}{4}$$

$$z = 4\sqrt{2} \left(\cos \frac{7π}{4} + i \sin \frac{7π}{4}\right)$$

Now, find the cube roots.

$$\sqrt[n]{z} = \sqrt[n]{r}\left(\cos \left(\frac{θ}{n} + \frac{2πk}{n}\right) + i \sin \left(\frac{θ}{n} + \frac{2πk}{n}\right)\right)$$

$$\sqrt[3]{z} = \sqrt[3]{4\sqrt{2}}\left(\cos \left(\frac{\frac{7π}{4}}{3} + \frac{2πk}{3}\right) + i \sin \left(\frac{\frac{7π}{4}}{3} + \frac{2πk}{3}\right)\right)$$

$$= \sqrt[3]{4\sqrt{2}}\left(\cos \left(\frac{7π}{12} + \frac{8πk}{12}\right) + i \sin \left(\frac{7π}{12} + \frac{8πk}{12}\right)\right)$$

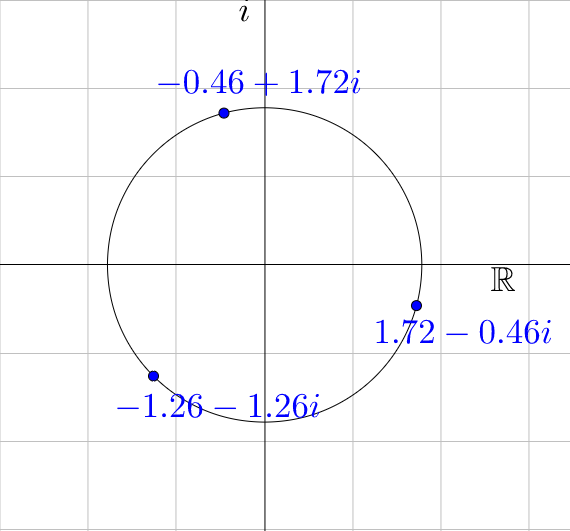
Let k = 0:

$$\sqrt[3]{4\sqrt{2}}\left(\cos \frac{7π}{12} + i \sin \frac{7π}{12}\right)$$

$$≈ -0.4612 + 1.7211i$$

Let k = 1:

$$\sqrt[3]{4\sqrt{2}}\left(\cos \frac{15π}{12} + i \sin \frac{15π}{12}\right)$$

$$≈ -1.2599 - 1.2599i$$

Let k = 2:

$$\sqrt[3]{4\sqrt{2}}\left(\cos \frac{23π}{12} + i \sin \frac{23π}{12}\right)$$

$$≈ 1.7211 - 0.4612i$$

Graph of the cube roots of z = 4 – 4i

If \(z = 8\left(\cos \frac{π}{6} + i \sin \frac{π}{6}\right)\), find \(\sqrt[3]{z}\). Write your answers in standard form.

Answers

1.970 + 0.347i, −1.286 + 1.532i, −0.684 − 1.879i

Lesson Summary
Multiply Complex Numbers in Trigonometric Form

Let z1 = r1(cos θ1 + i sin θ1) and z2 = r2(cos θ2 + i sin θ2) be complex numbers.

z1z2 = r1r2(cos(θ1 + θ2) + i sin(θ1 + θ2))

If θ1 + θ2 > 2π, then subtract 2π to get a coterminal angle between 0 and 2π.

Divide Complex Numbers in Trigonometric Form

Let z1 = r1(cos θ1 + i sin θ1) and z2 = r2(cos θ2 + i sin θ2) be complex numbers.

$$\frac{z_1}{z_2} = \frac{r_1}{r_2}\left(\cos \left(θ_1 - θ_2\right) + i \sin \left(θ_1 - θ_2\right)\right)$$

If θ1 − θ2 < 0, then add 2π to get a coterminal angle between 0 and 2π.

Exponents on Complex Numbers in Trigonometric Form

Let z = r(cos θ + i sin θ) be a complex number.

zn = rn(cos(nθ) + i sin(nθ))

If nθ > 2π, then subtract 2π to get a coterminal angle between 0 and 2π.

Roots of Complex Numbers

Let z = r(cos θ + i sin θ)

$$\sqrt[n]{z} = \sqrt[n]{r}\left(\cos \left(\frac{θ}{n} + \frac{2πk}{n}\right) + i \sin \left(\frac{θ}{n} + \frac{2πk}{n}\right)\right)$$

Where k = 0, 1, 2, …, n – 1

Helpful videos about this lesson.

Practice Exercises

  1. Derive the exponent formula when n = 2.
  2. Multiply the complex numbers. If they are in standard form, first convert to trigonometric form. Write the product in standard form rounded to 4 decimal places.
  3. \(\left(4\left(\cos \frac{π}{4} + i \sin \frac{π}{4}\right)\right)\left(5\left(\cos \frac{2π}{3} + i \sin \frac{2π}{3}\right)\right)\)
  4. \(\left(3\left(\cos \frac{π}{2} + i \sin \frac{π}{2}\right)\right)\left(10\left(\cos \frac{3π}{2} + i \sin \frac{3π}{2}\right)\right)\)
  5. (2 + i)(−3 + 4i)
  6. Divide the complex numbers. If they are in standard form, first convert to trigonometric form. Write the quotient in standard form rounded to 4 decimal places.
  7. \(\frac{4\left(\cos \frac{π}{4} + i \sin \frac{π}{4}\right)}{2\left(\cos \frac{3π}{4} + i \sin \frac{3π}{4}\right)}\)
  8. \(\frac{12\left(\cos \frac{5π}{3} + i \sin \frac{5π}{3}\right)}{3\left(\cos \frac{π}{6} + i \sin \frac{π}{6}\right)}\)
  9. \(\frac{2 + 2i}{1 - \sqrt{3}i}\)
  10. \(\frac{3}{4 - i}\)
  11. Evaluate the exponents of complex numbers. If they are in standard form, first convert to trigonometric form. Write the result in standard form rounded to 4 decimal places.
  12. \(\left(3\left(\cos \frac{π}{6} + i \sin \frac{π}{6}\right)\right)^2\)
  13. \(\left(2\left(\cos \frac{2π}{3} + i \sin \frac{2π}{3}\right)\right)^3\)
  14. \(\left(2\sqrt{3} + 2i\right)^4\)
  15. Find all the roots of the complex numbers. Write the result in standard form rounded to 4 decimal places.
  16. \(\sqrt[3]{64\left(\cos \frac{π}{4} + i \sin \frac{π}{4}\right)}\)
  17. \(\sqrt[4]{81\left(\cos \frac{2π}{3} + i \sin \frac{2π}{3}\right)}\)
  18. \(\sqrt{3 + 4i}\)
  19. \(\sqrt[4]{3i}\)
  20. Mixed Review
  21. (6-06) Find |2 + 5i|.
  22. (6-06) Write \(5 - 5\sqrt{3}i\) in trigonometric form.
  23. (6-05) Evaluate ⟨2, 5⟩ · ⟨−3, 4⟩.
  24. (6-04) Write 30 m at S 60° E in trigonometric form.
  25. (6-03) Evaluate ⟨2, 5⟩ + ⟨−3, 4⟩.

Answers

  1. Let \(z = r\left(\cos θ + i \sin θ\right)\) be a complex number. Squaring is multiplying by itself, so use the multiplication rule. \(z_1 z_2 = r_1 r_2\left(\cos \left(θ_1 + θ_2\right) + i \sin \left(θ_1 + θ_2\right)\right)\) but let z1 and z2 both simply be z. \(z^2 = z \cdot z = r \cdot r\left(\cos \left(θ + θ\right) + i \sin \left(θ + θ\right)\right)\) \(= r^2\left(\cos \left(2θ\right) + i \sin \left(2θ\right)\right)\)
  2. −19.3185 + 5.1764i
  3. 30
  4. −10 + 5i
  5. −2i
  6. −4i
  7. −0.3660 + 1.3660i
  8. 0.7059 + 0.1765i
  9. 4.5 + 7.7942i
  10. 8
  11. −128 + 221.7025i
  12. 3.8637 + 1.0353i, −2.8284 + 2.8284i, −1.0353 − 3.8637i
  13. 2.5981 + 1.5i, −1.5 + 2.5981i, −2.5981 − 1.5i, 1.5 − 2.5981i
  14. 2 + i, −2 − i
  15. 1.2159 + 0.5036i, −0.5036 + 1.2159i, −1.2159 − 0.5036i, 0.5036 − 1.2159i
  16. \(\sqrt{29}\)
  17. \(10\left(\cos \frac{5π}{3} + i \sin \frac{5π}{3}\right)\)
  18. 14
  19. 30⟨cos 330°, sin 330°⟩
  20. ⟨−1, 9⟩