Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Nehemiah said, “Go and enjoy choice food and sweet drinks, and send some to those who have nothing prepared. This day is holy to our Lord. Do not grieve, for the joy of the Lord is your strength.” Nehemiah 8:10 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.5.2, PC.6.7
Satellites orbit the earth or other planets in ellipses with the planet at one focus. Because everything is space is moving in curved paths and contain round objects, it is logical to use a round coordinate system to describe space. It turns out that all conic sections can be described by one general polar equation.
Locus of a point in the plane that moves so its distance from a fixed point (focus) is in a constant ratio to its distance from a fixed line (directrix).
The ratio is the eccentricity (e).
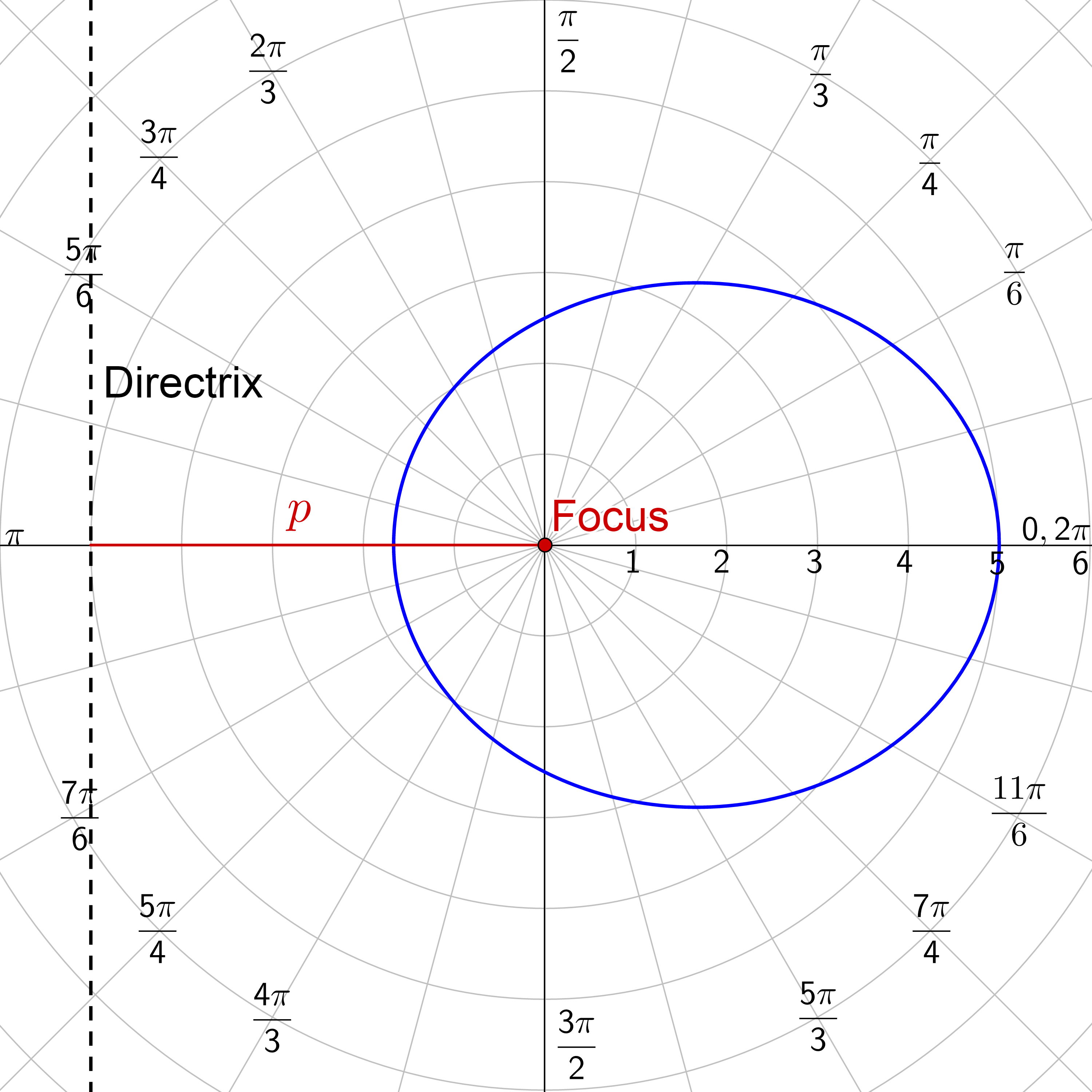
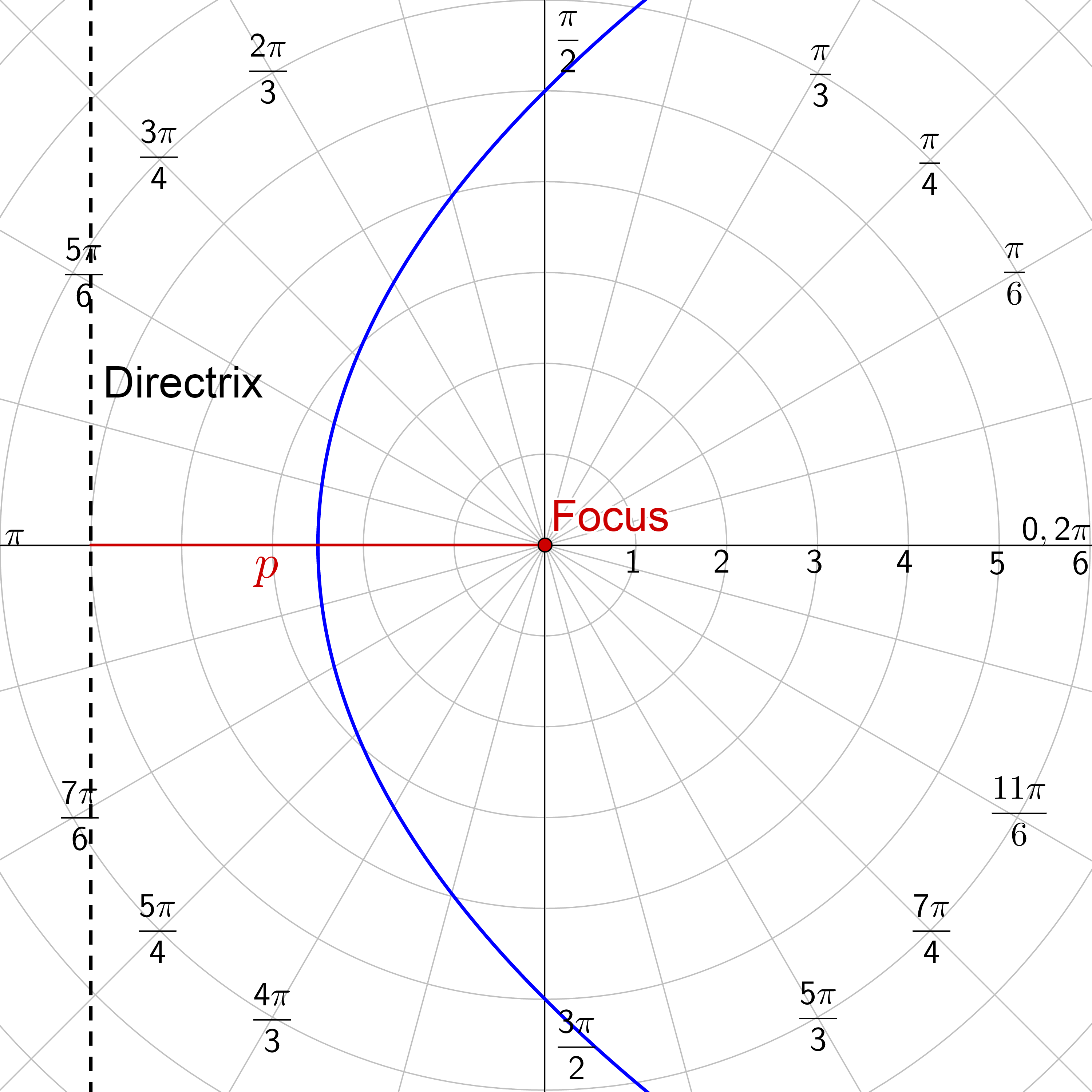
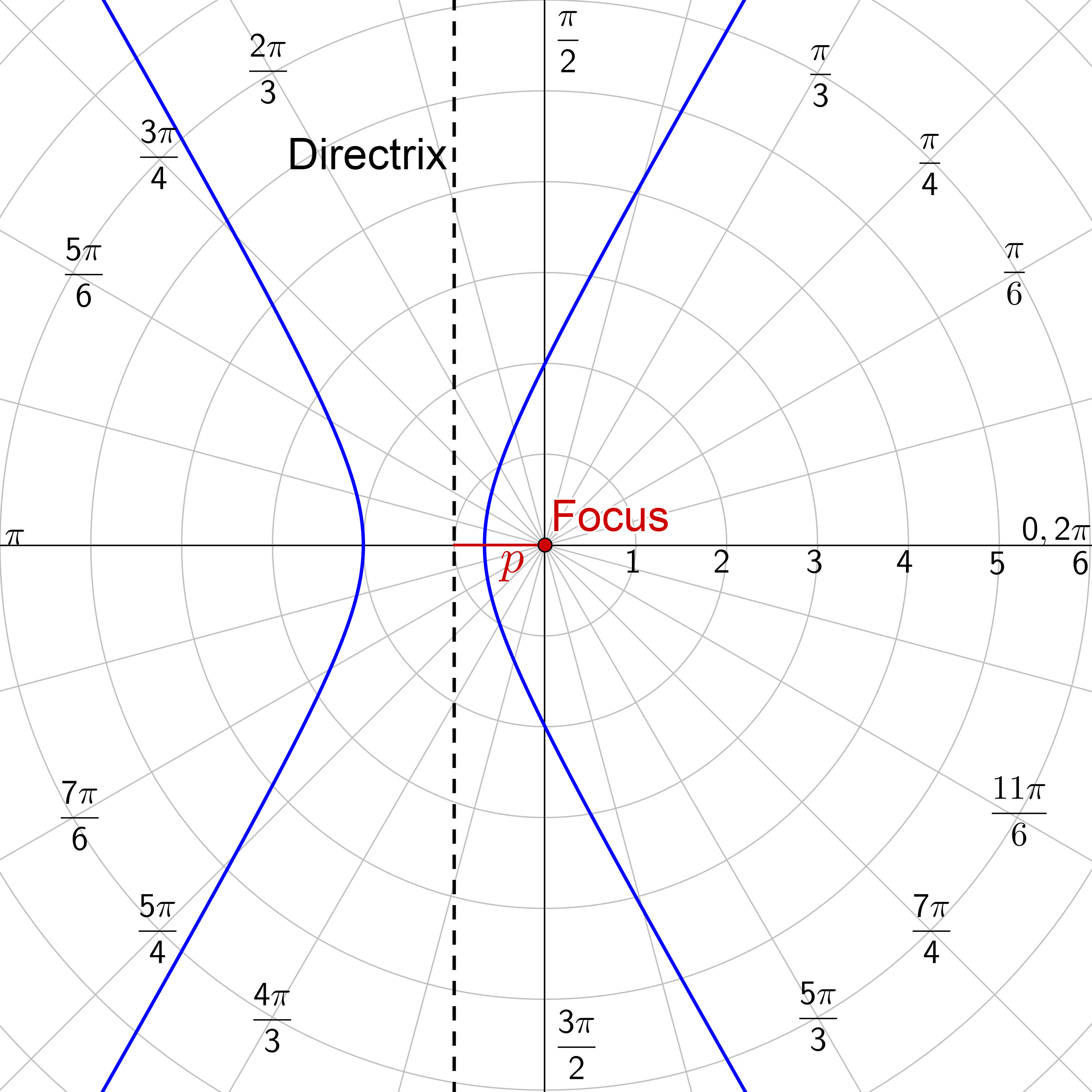
For all of these, a focus is at the pole.
| Vertical Directrix | |
|---|---|
| Directrix right of pole | Directrix left of pole |
| $$ r = \frac{ep}{1+e \cos θ} $$ | $$ r = \frac{ep}{1-e \cos θ} $$ |
 |
|
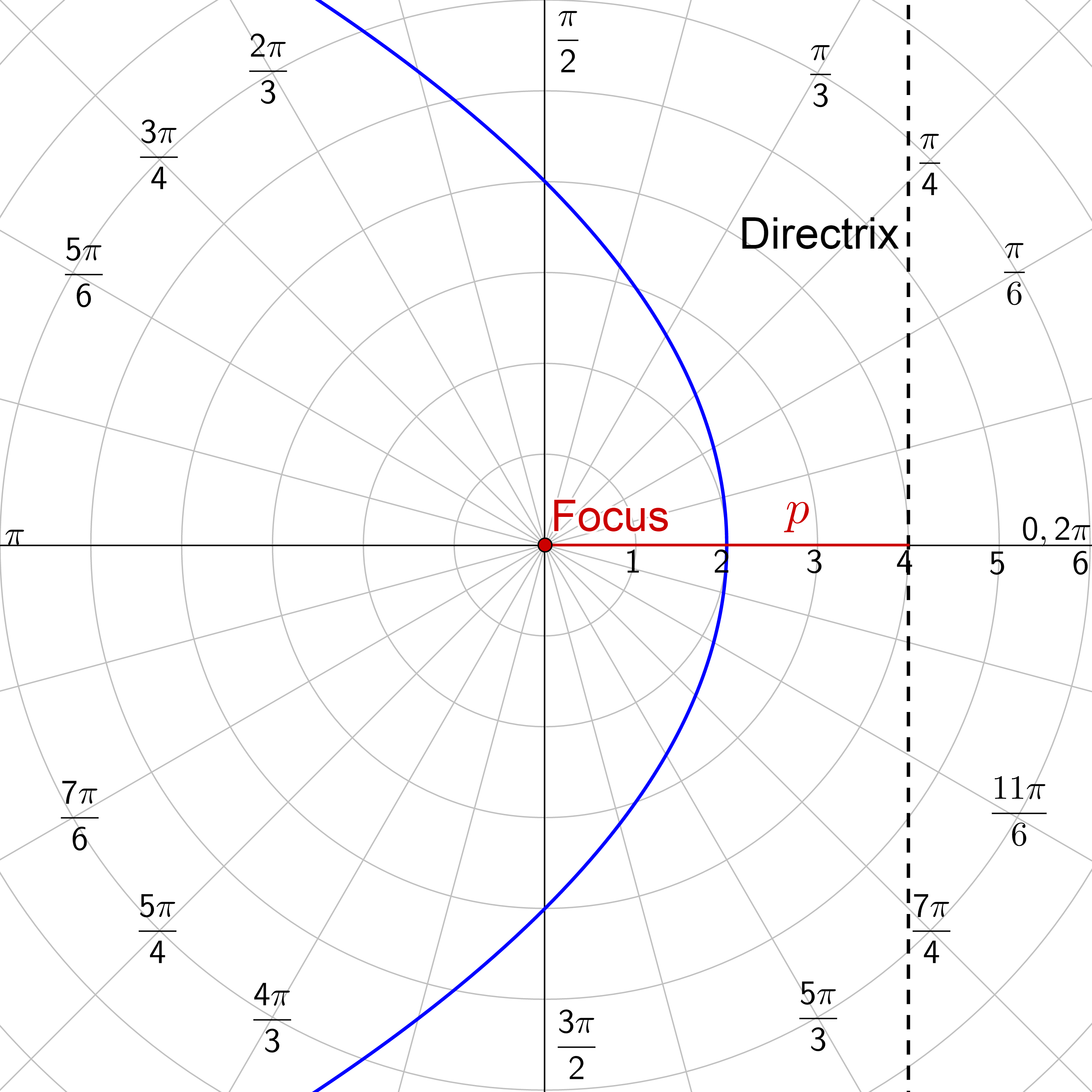| Horizontal Directrix | |
|---|---|
| Directrix above pole | Directrix below pole |
| $$ r = \frac{ep}{1+e \sin θ} $$ | $$ r = \frac{ep}{1-e \sin θ} $$ |
 |
 |
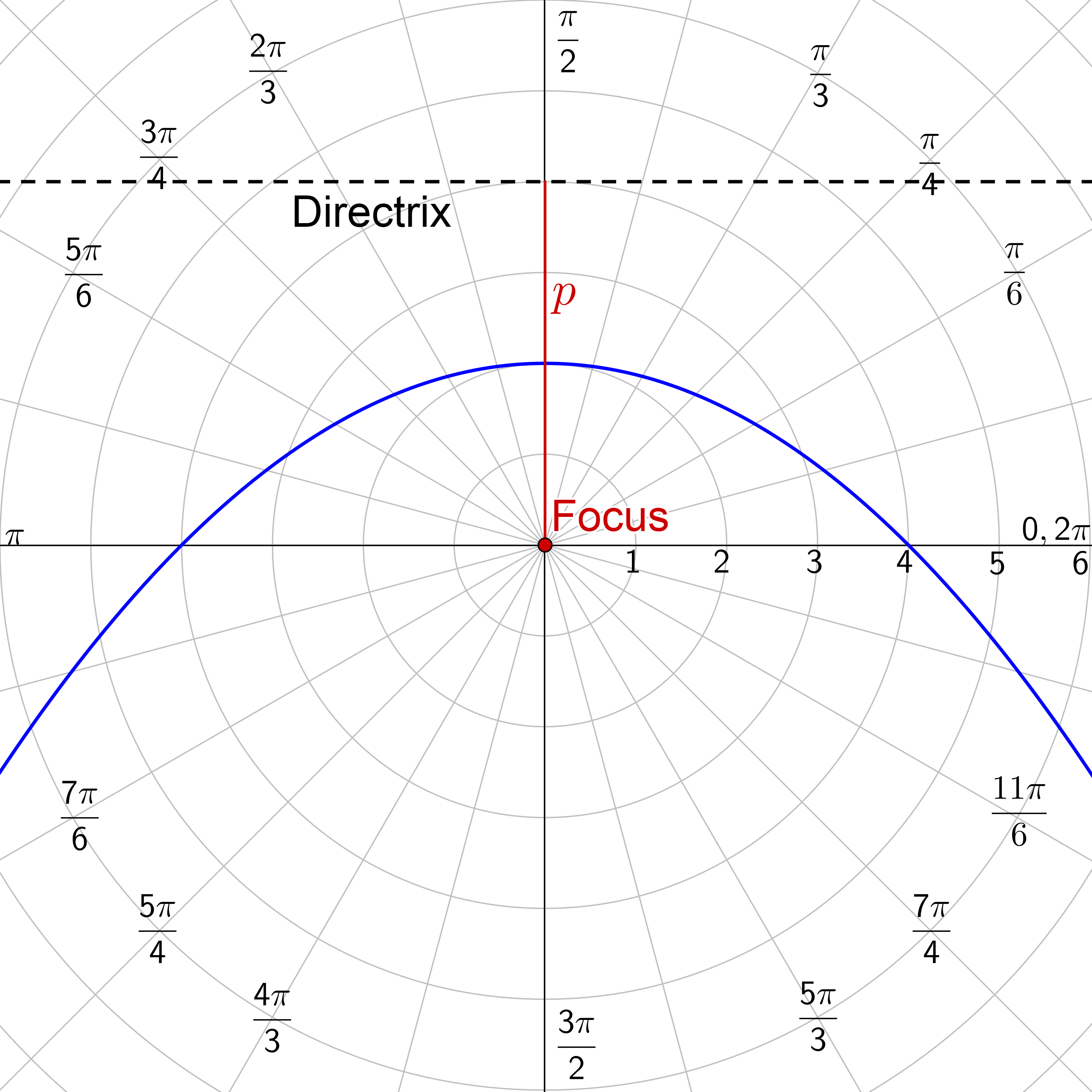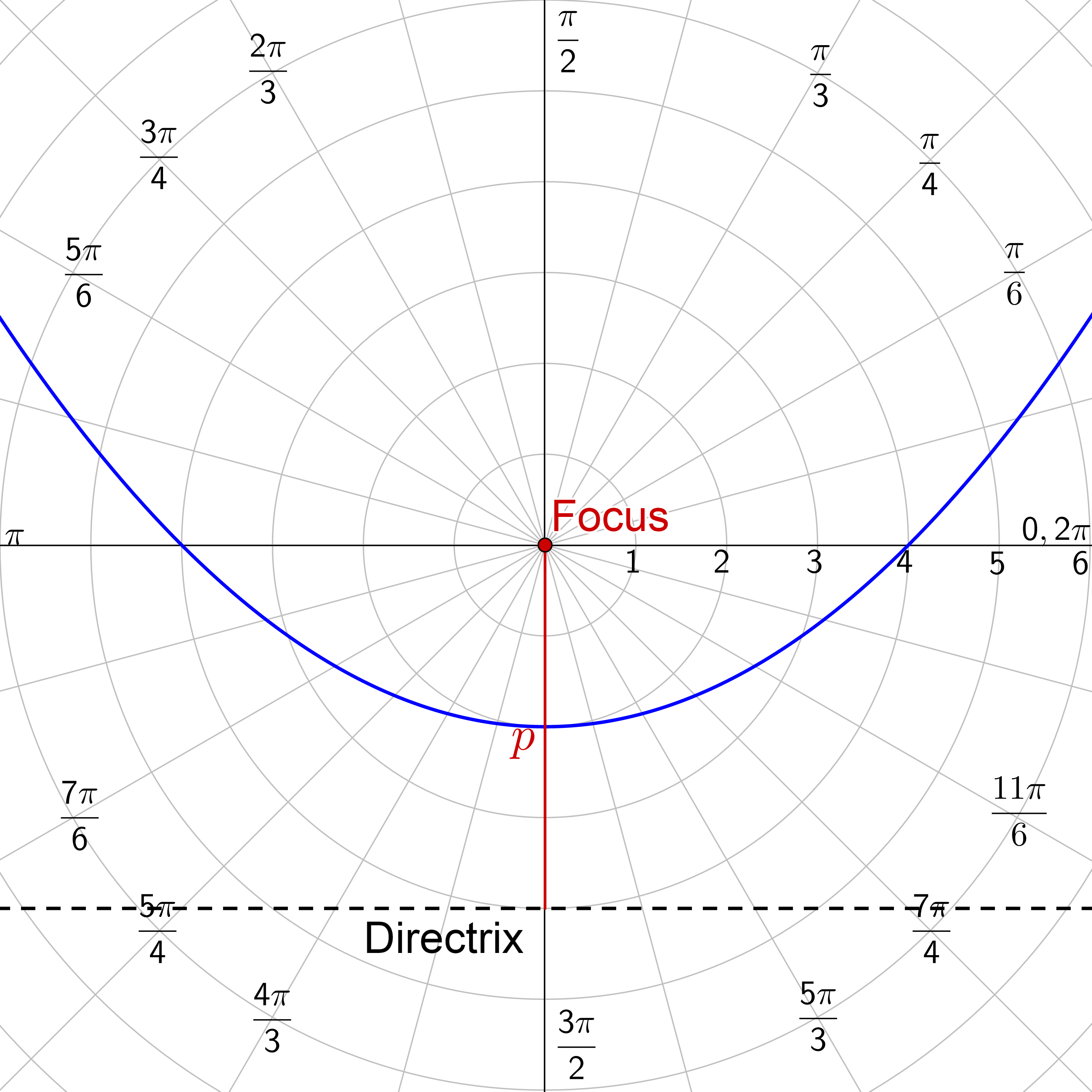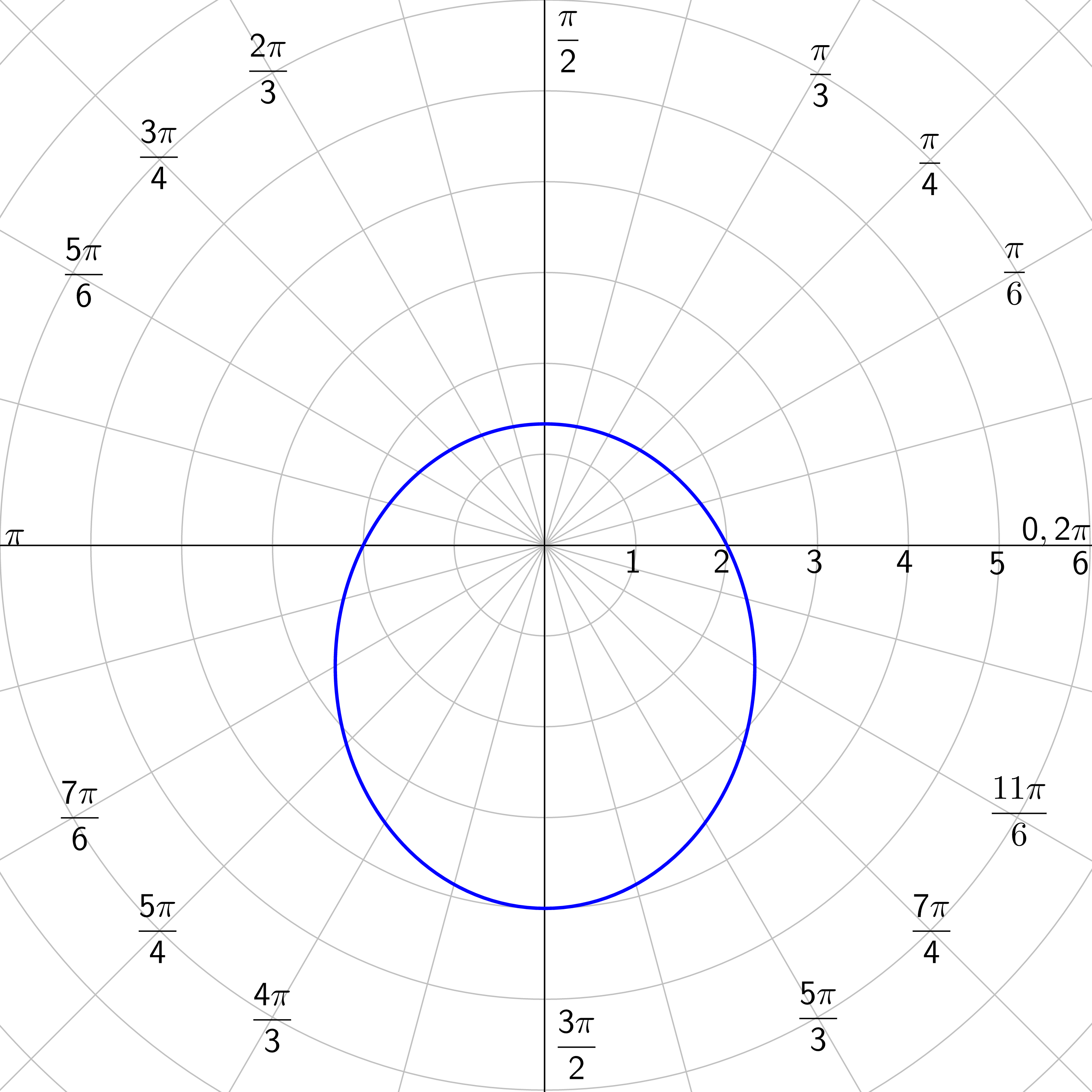
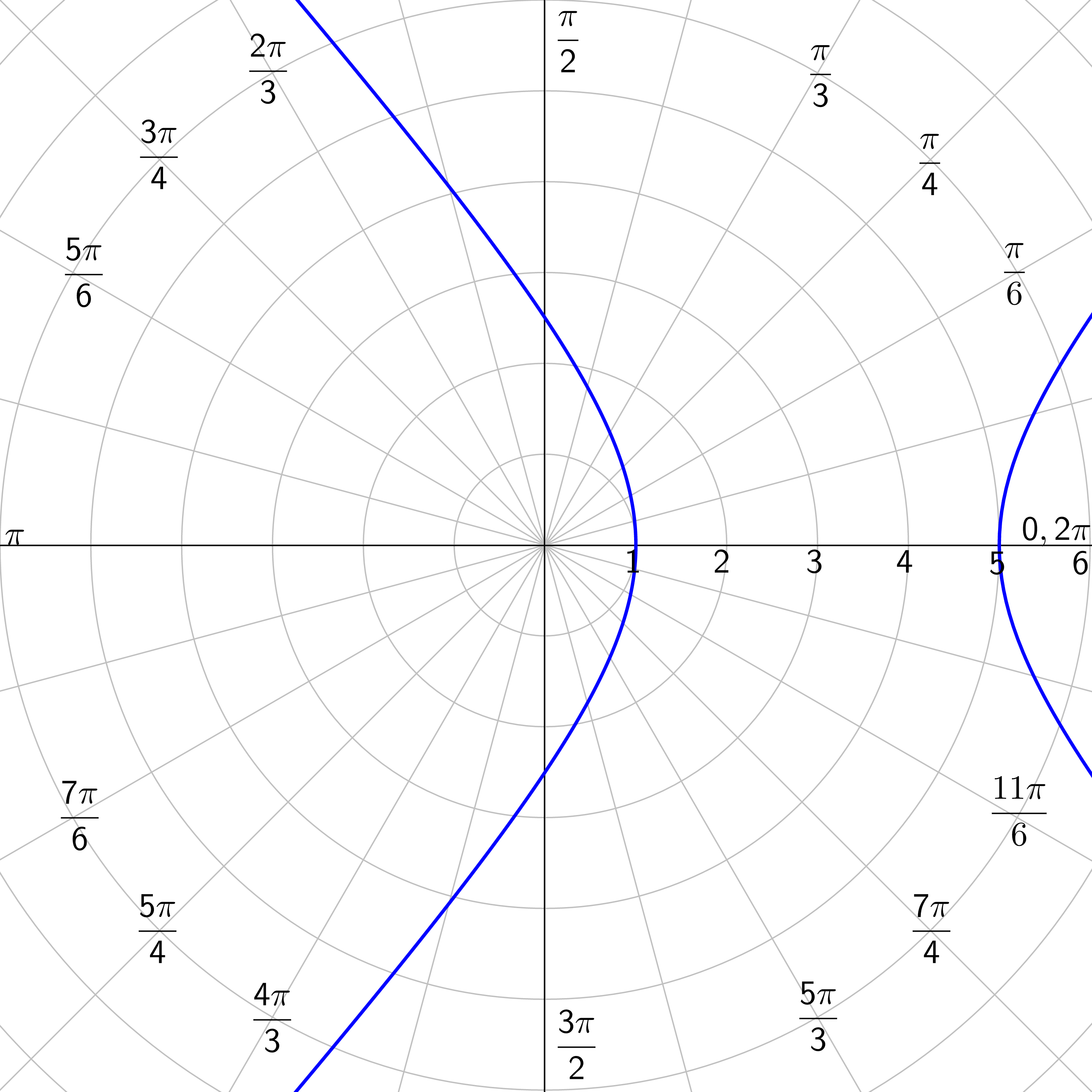
Identify the type of conic of \(r = \frac{5}{2+4 \sin θ}\).
Solution
All the forms of a conic equation start with a 1 in the denominator. To get that, multiply the numerator and denominator by \(\frac{1}{2}\).
$$ r = \frac{5}{2+4 \sin θ} $$
$$ r = \frac{\frac{5}{2}}{1 + 2 \sin θ} $$
The coefficient of the trig function is e. In this case, e = 2 > 1 so it is a hyperbola. The denominator has a \(+ \sin θ\) which looks like \(r = \frac{ep}{1+e \sin θ}\). So the conic is a hyperbola with horizontal directrix above the pole.
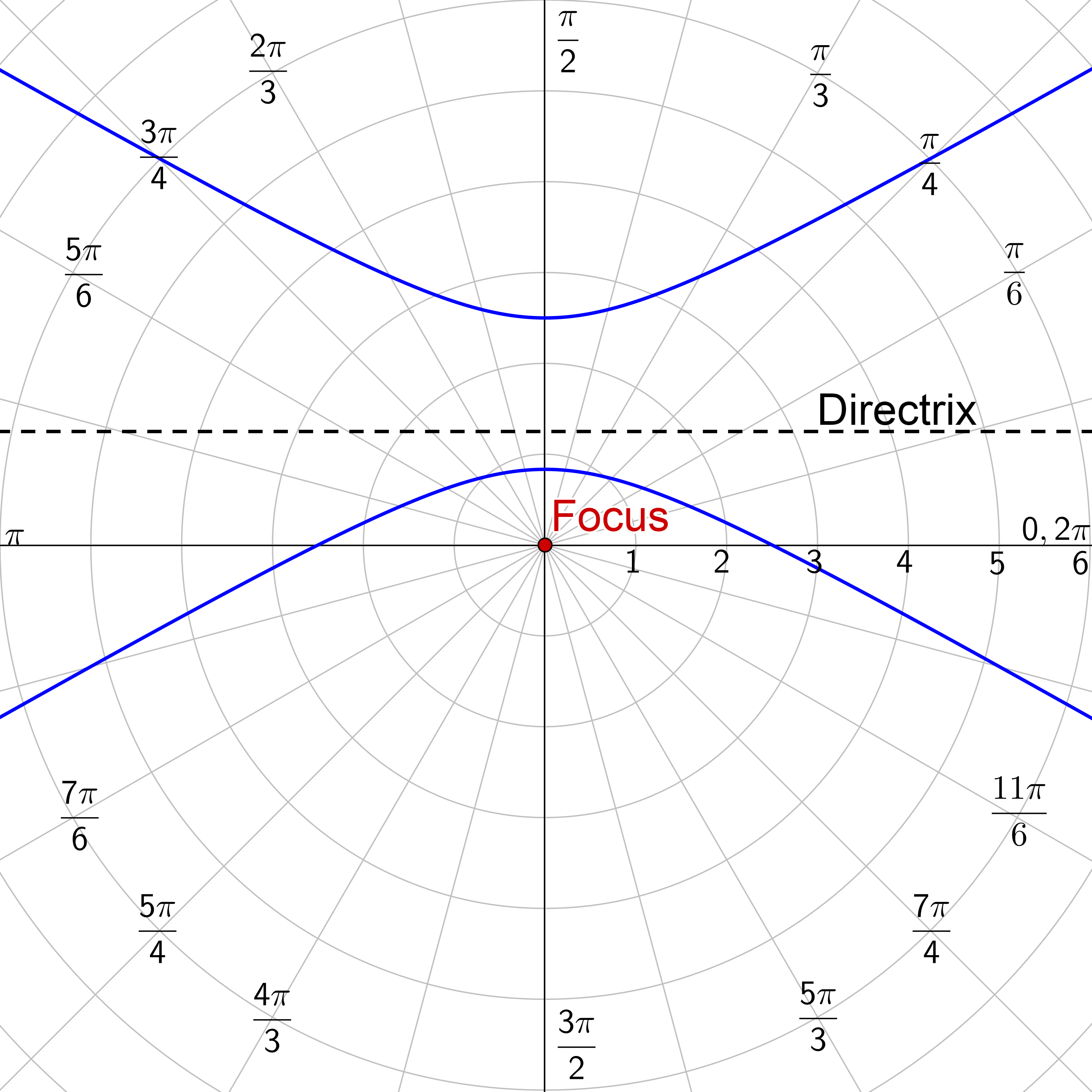
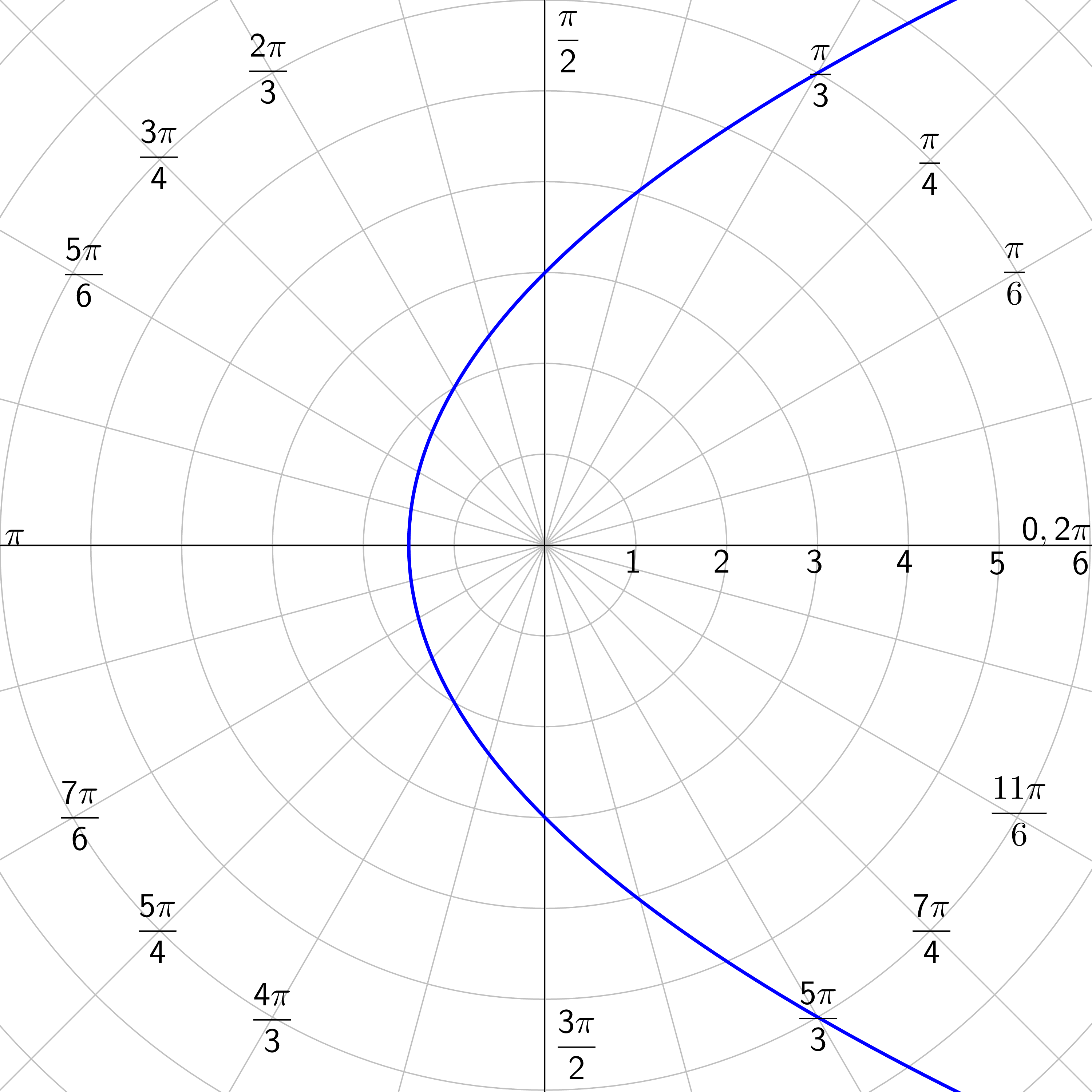
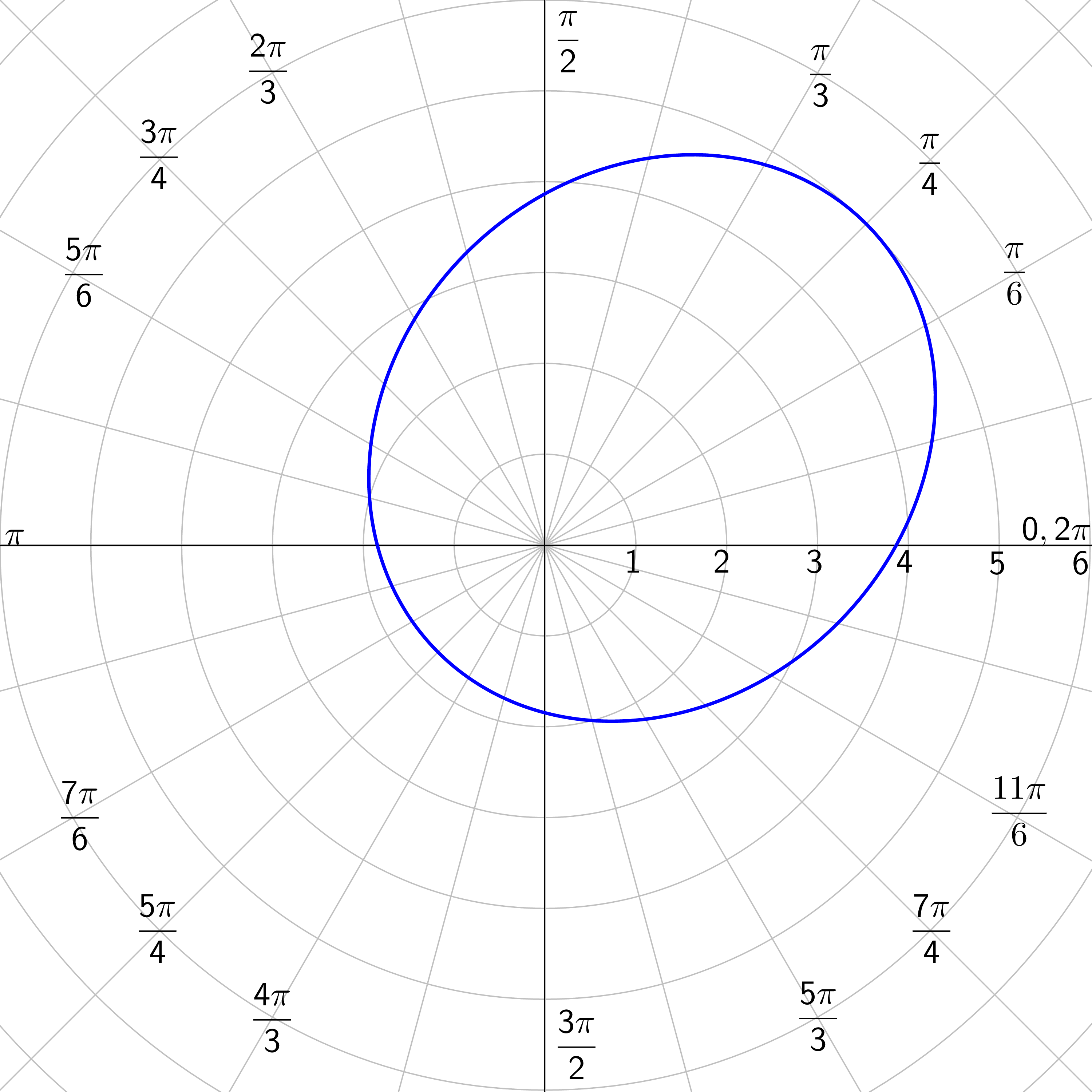
Identify the type of conic of \(r = \frac{5}{3-\cos θ}\) and then graph it.
Solution
All the forms of a conic equation start with a 1 in the denominator. To get that, multiply the numerator and denominator by \(\frac{1}{3}\).
$$ r = \frac{5}{3-\cos θ} $$
$$ r = \frac{\frac{5}{3}}{1 - \frac{1}{3} \cos θ} $$
The coefficient of the trig function is e. In this case, \(e = \frac{1}{3} < 1\) so it is a ellipse. The denominator has a \(- \cos θ\) which looks like \(r = \frac{ep}{1-e \cos θ}\). So the conic is a ellipse with vertical directrix left of the pole.
Graph the ellipse by making a table of values.
| r | 2.5 | 2.46 | 2.34 | 2.18 | 2 | 1.82 | 1.67 | 1.53 | 1.43 | 1.35 | 1.29 | 1.26 | 1.25 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| θ | 0 | \(\frac{π}{12}\) | \(\frac{π}{6}\) | \(\frac{π}{4}\) | \(\frac{π}{3}\) | \(\frac{5π}{12}\) | \(\frac{π}{2}\) | \(\frac{7π}{12}\) | \(\frac{2π}{3}\) | \(\frac{3π}{4}\) | \(\frac{5π}{6}\) | \(\frac{11π}{12}\) | \(π\) |
| r | 1.26 | 1.29 | 1.35 | 1.43 | 1.53 | 1.67 | 1.82 | 2 | 2.18 | 2.34 | 2.46 | 2.5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| θ | \(\frac{13π}{12}\) | \(\frac{7π}{6}\) | \(\frac{5π}{4}\) | \(\frac{4π}{3}\) | \(\frac{17π}{12}\) | \(\frac{3π}{2}\) | \(\frac{19π}{12}\) | \(\frac{5π}{3}\) | \(\frac{7π}{4}\) | \(\frac{11π}{6}\) | \(\frac{23π}{12}\) | \(2π\) |
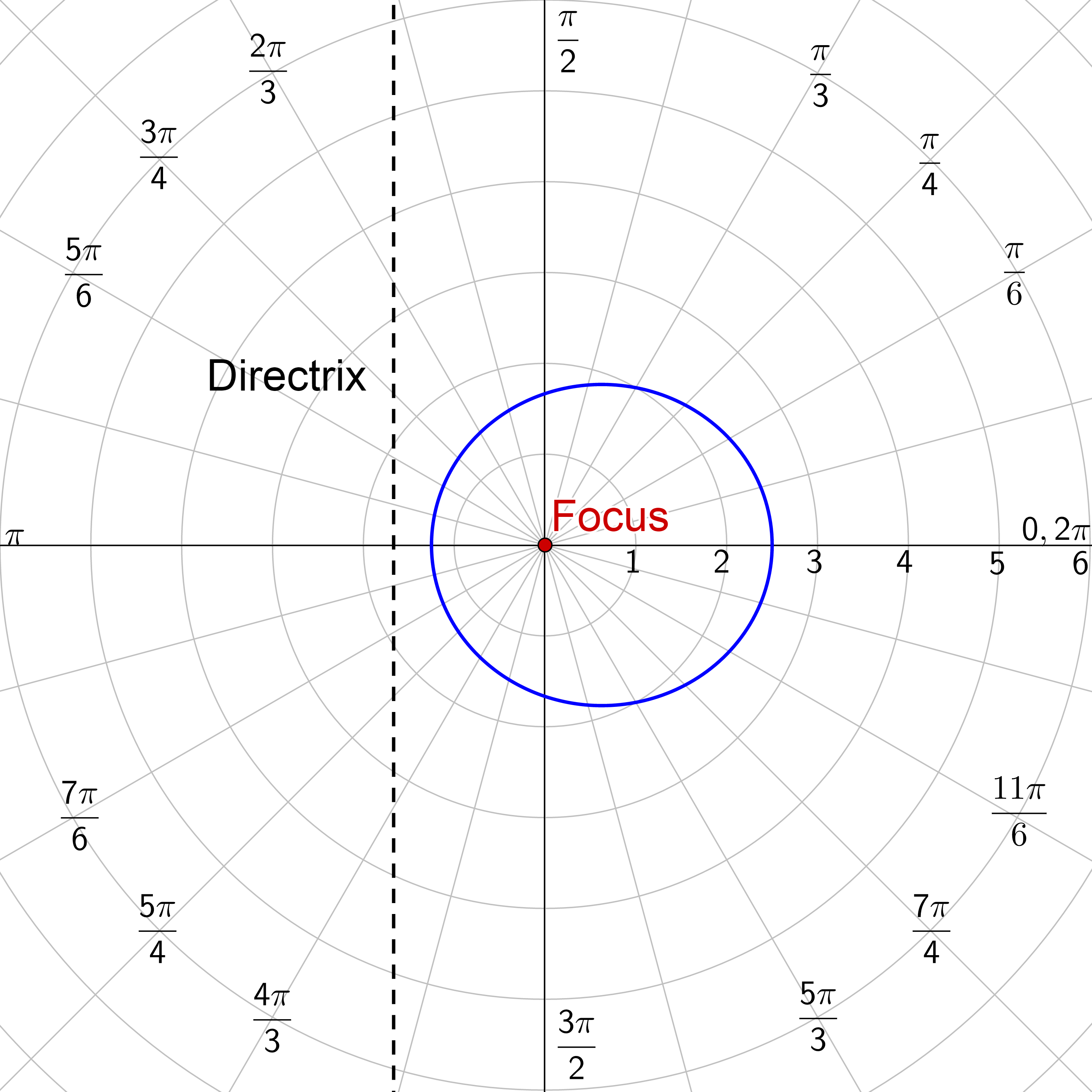
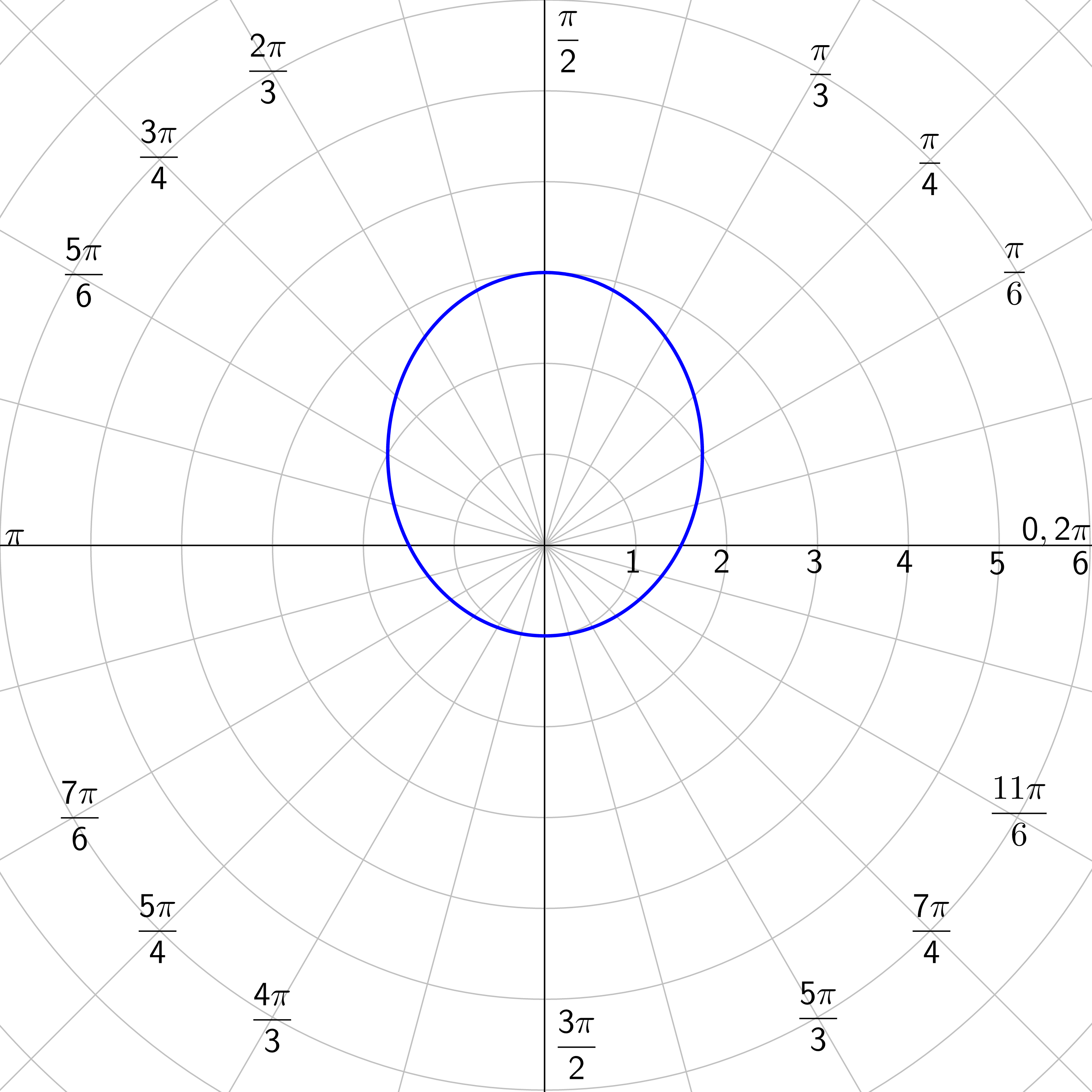
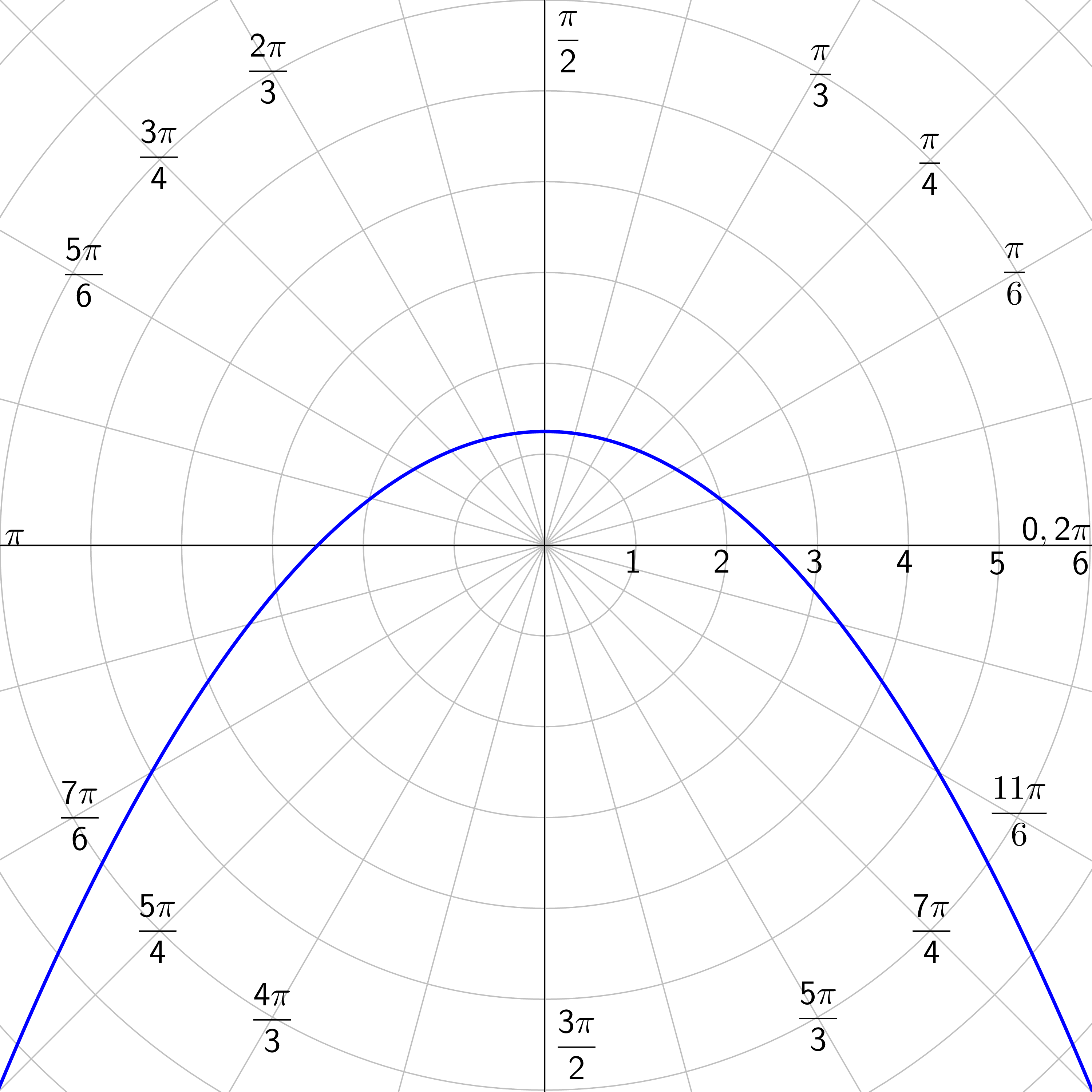
Identify the type of conic of \(r = \frac{4}{1-\sin θ}\).
Answer
Parabola with horizontal directrix below the pole
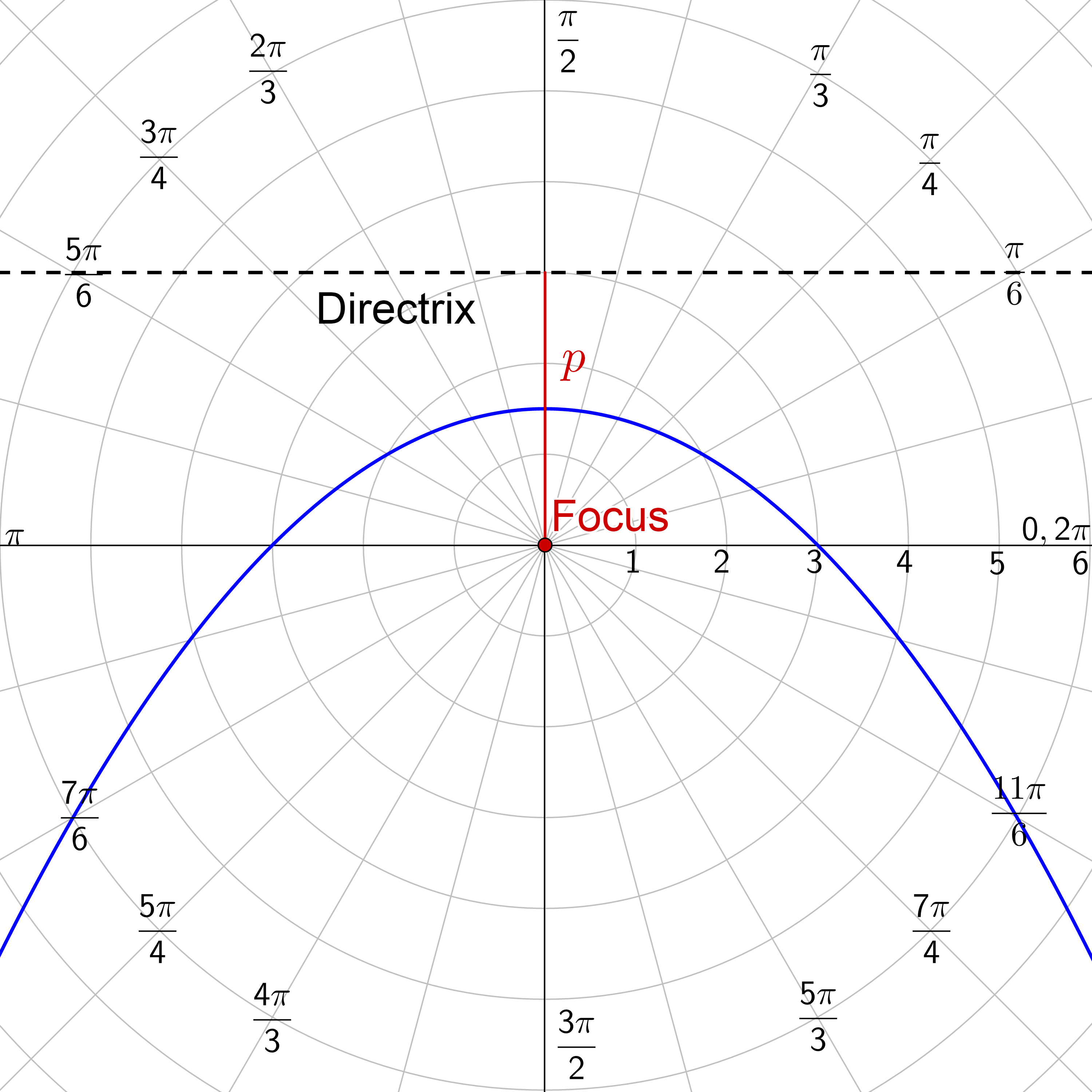
Find the polar equation of the parabola whose focus is the pole and directrix is the line \(y = 3\).
Solution
Since the focus is the origin and the directrix is y = 3, the directrix is horizontal and above the pole. Thus, our equation is
$$ r = \frac{ep}{1 + e \sin θ} $$
Since it is a parabola, e = 1. p is the distance from the focus (0, 0) to the directrix y = 3, so p = 3. Fill those in and the equation becomes
$$ r = \frac{1(3)}{1 + 1 \sin θ} $$
$$ r = \frac{3}{1 + \sin θ} $$
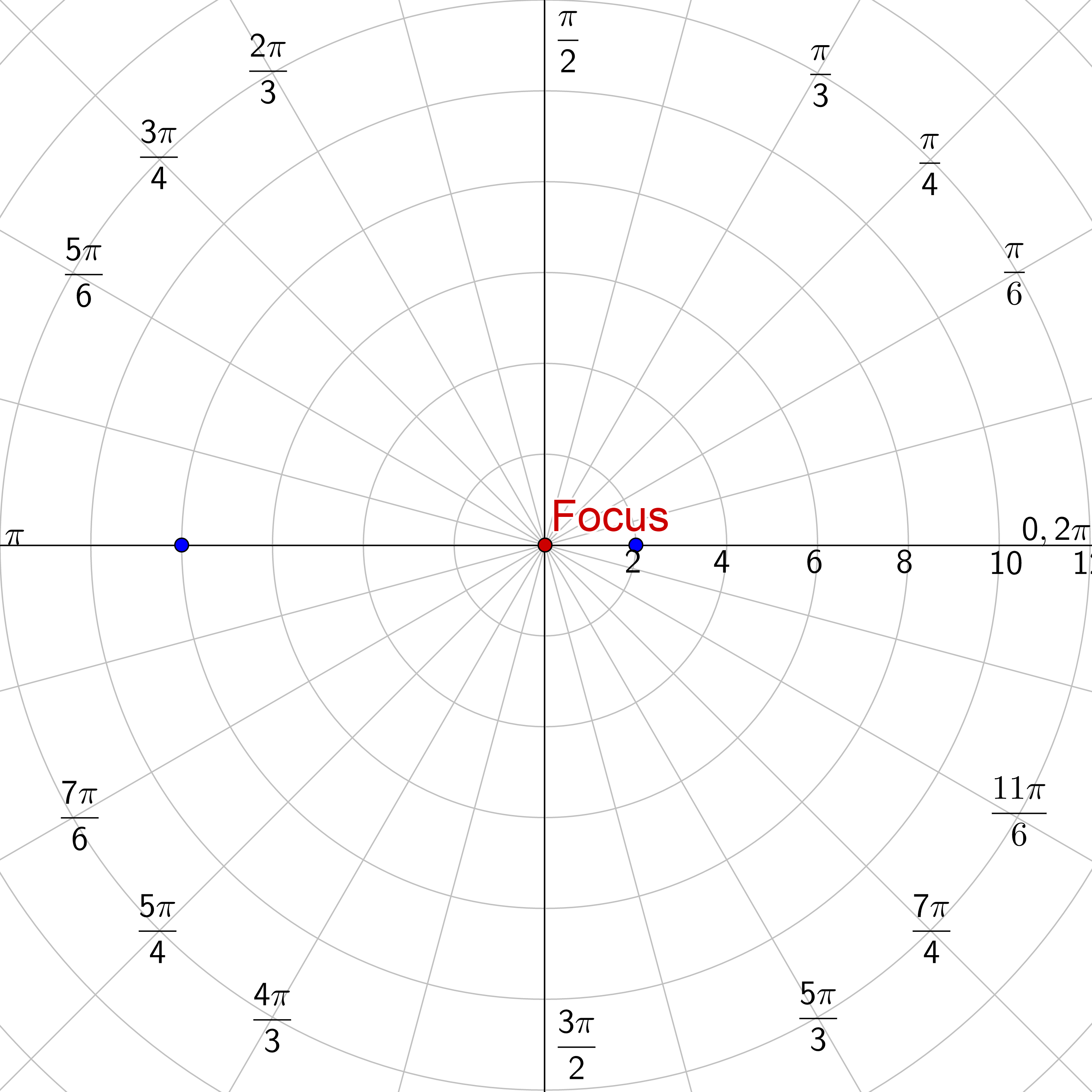
Find the polar equation of the ellipse whose focus is the pole and has vertices (2, 0) and (8, π).
Solution
Draw a quick sketch of the points and draw the primary axis of the ellipse. Remember the points are in polar format.
The directrix will be to the right and the ellipse will bend away from it. So the directrix is vertical and to the right of the origin.
$$ r = \frac{ep}{1 + e \cos θ} $$
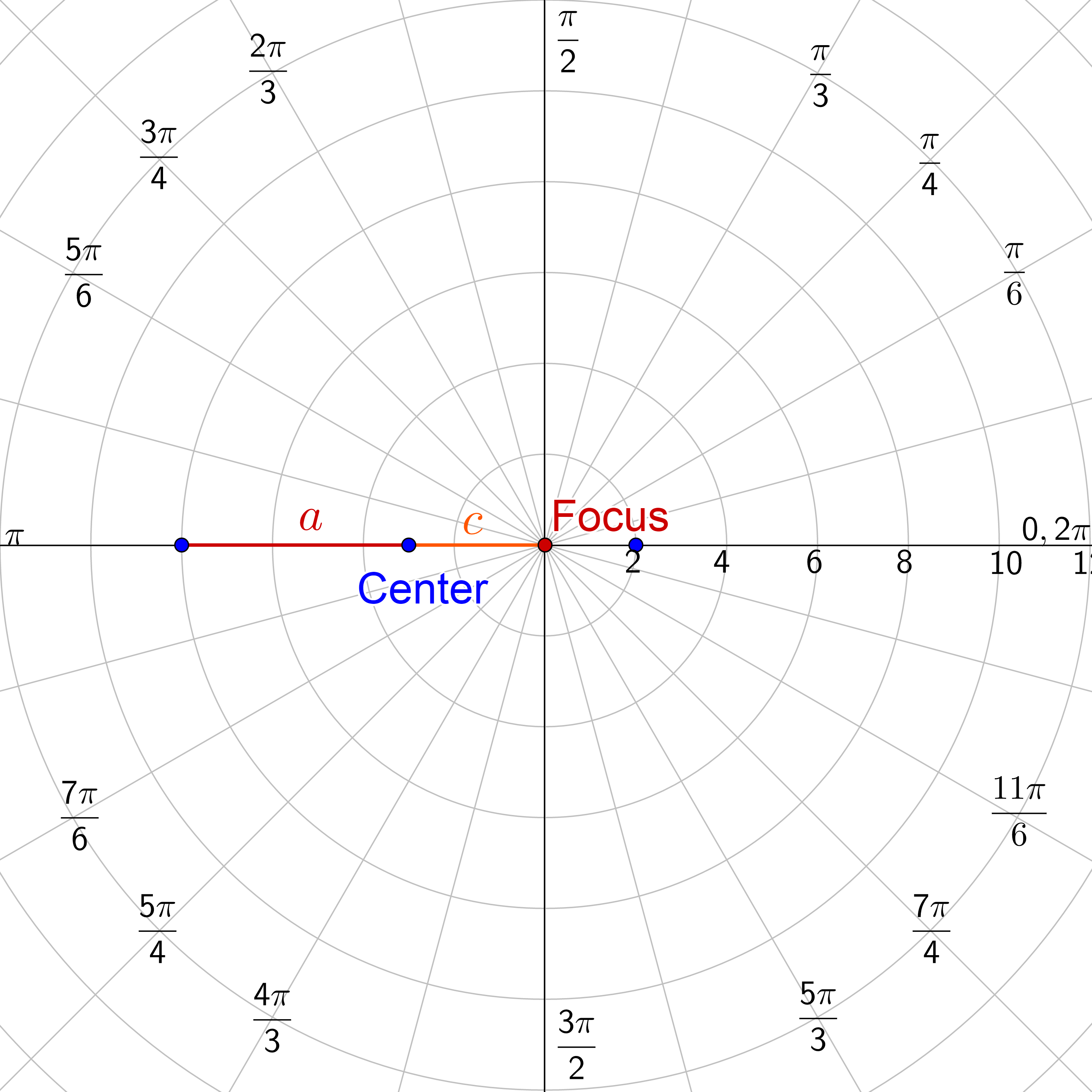
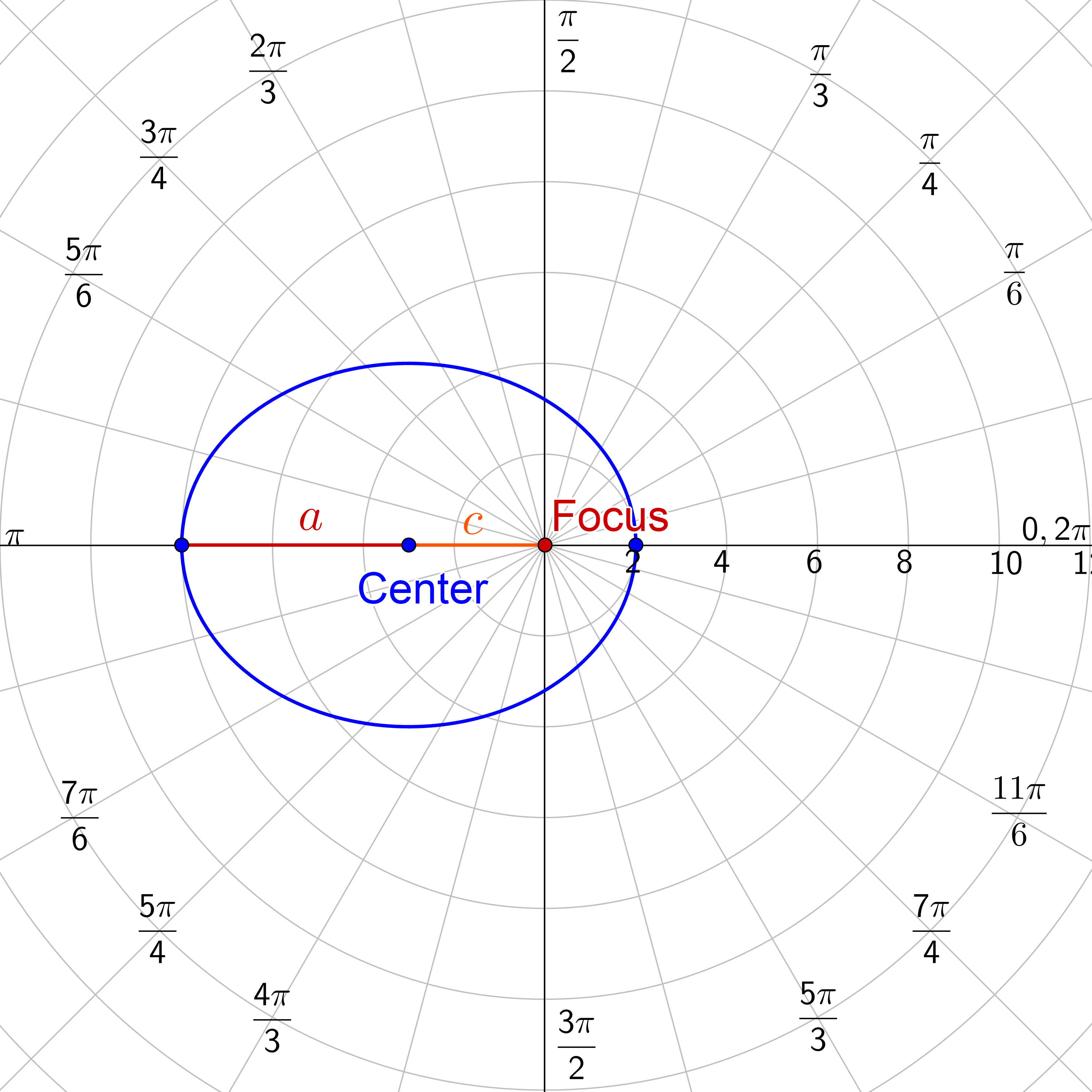
The center is halfway between the two vertices. a is the distance from the center to vertex, and c is the distance from the center to the focus. Remember from before that \(e = \frac{c}{a}\). In this case, a = 5 and c = 3, so \(e = \frac{3}{5}\). Fill this in and the equation becomes
$$ r = \frac{\frac{3}{5}p}{1 + \frac{3}{5} \cos θ} $$
Multiply numerator and denominator by 5 to remove fractions.
$$ r = \frac{3p}{5 + 3 \cos θ} $$
Now plug in a vertex point such as (2, 0) and solve for p.
$$ 2 = \frac{3p}{5 + 3 \cos 0} $$
$$ 2 = \frac{3p}{8} $$
$$ 16 = 3p $$
$$ \frac{16}{3} = p $$
Plug this into \(r = \frac{3p}{5 + 3 \cos θ}\) and simplify to get the final equation.
$$ r = \frac{3\left(\frac{16}{3}\right)}{5 + 3 \cos θ} $$
$$ r = \frac{16}{5 + 3 \cos θ} $$
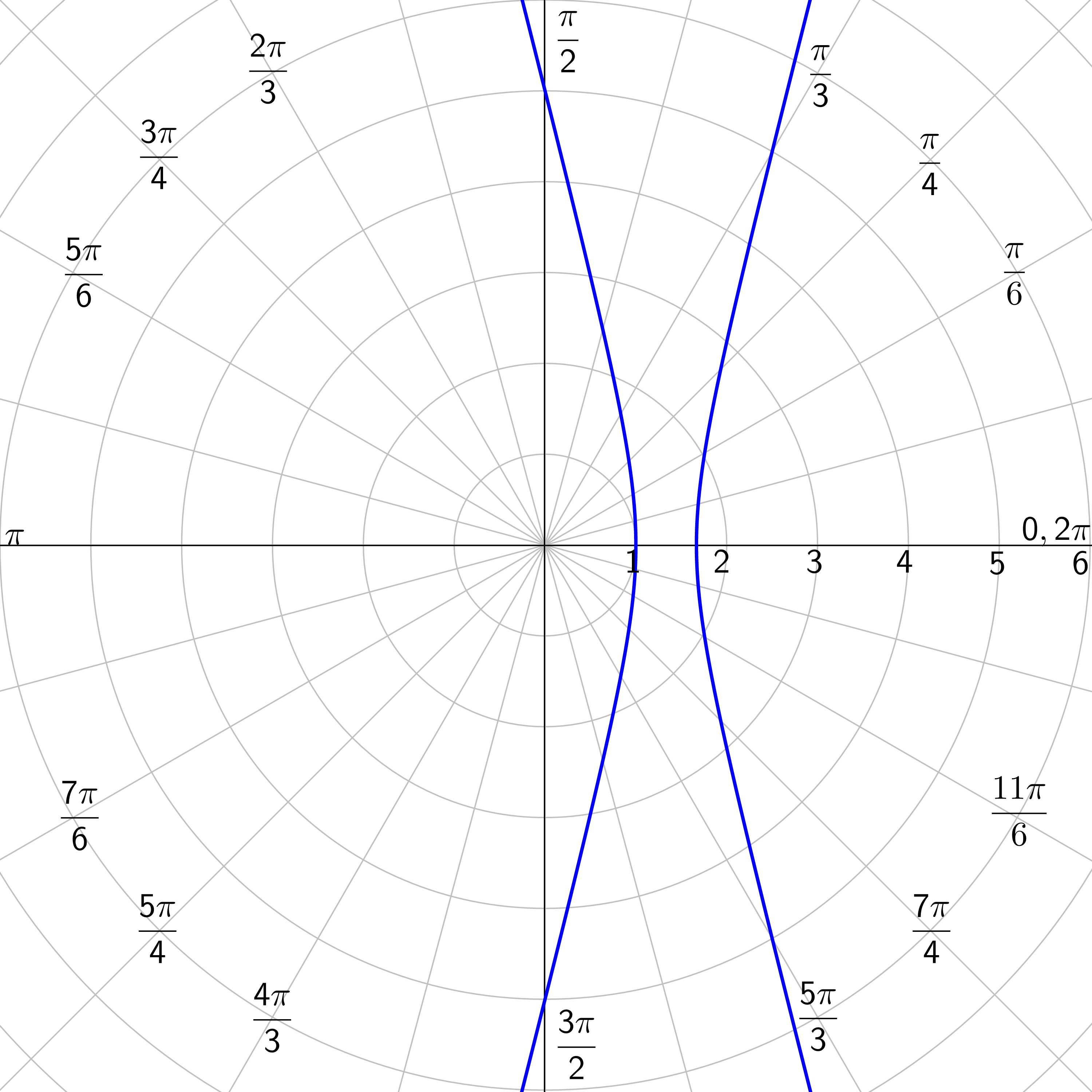
Find the polar equation of the hyperbola whose focus is the pole and has vertices \(\left(1, \frac{3π}{2}\right)\) and \(\left(9, \frac{3π}{2}\right)\).
Answer
\(r = \frac{9}{4 - 5 \sin θ}\)
Locus of a point in the plane that moves so its distance from a fixed point (focus) is in a constant ratio to its distance from a fixed line (directrix).
The ratio is the eccentricity (e).
For all of these, a focus is at the pole.
| Vertical Directrix | |
|---|---|
| Directrix right of pole | Directrix left of pole |
| $$ r = \frac{ep}{1+e \cos θ} $$ | $$ r = \frac{ep}{1-e \cos θ} $$ |
|
|
| Horizontal Directrix | |
|---|---|
| Directrix above pole | Directrix below pole |
| $$ r = \frac{ep}{1+e \sin θ} $$ | $$ r = \frac{ep}{1-e \sin θ} $$ |
|
|
Helpful videos about this lesson.
