Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Peace I leave with you; my peace I give you. I do not give to you as the world gives. Do not let your hearts be troubled and do not be afraid. John 14:27 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.5.2
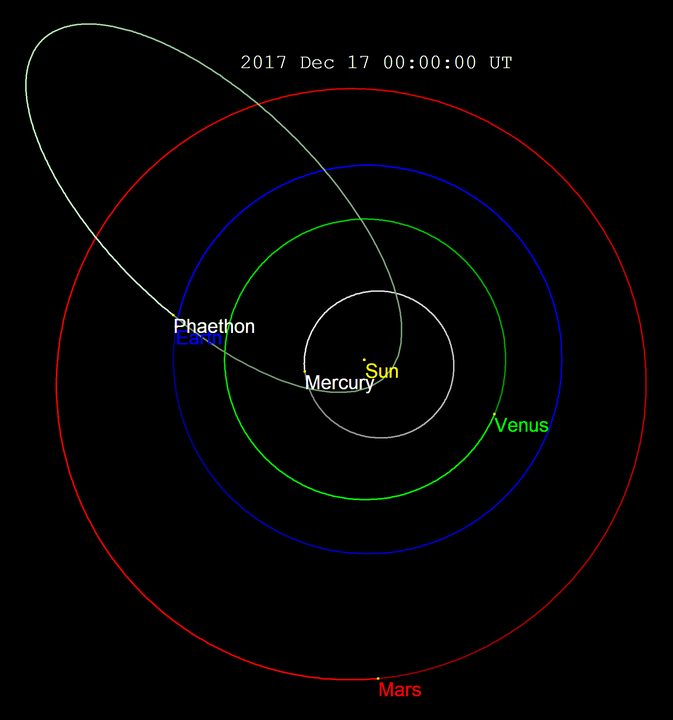
All the planet and comets such as Phaethon, orbit the sun in elliptical orbits. A graph of their orbits can be made by plotting their positions over time and then connecting the points. Since ellipses are curves, it makes sense to use a coordinate system that is curved. This lesson is about graphing polar equations.
Graph polar equations by making a table. The first column is r and the second column is θ. Choose values of θ and calculate the values of r. Then plot all the points. Make sure there are enough points to see the entire shape. Last, draw a smooth curve through the points.
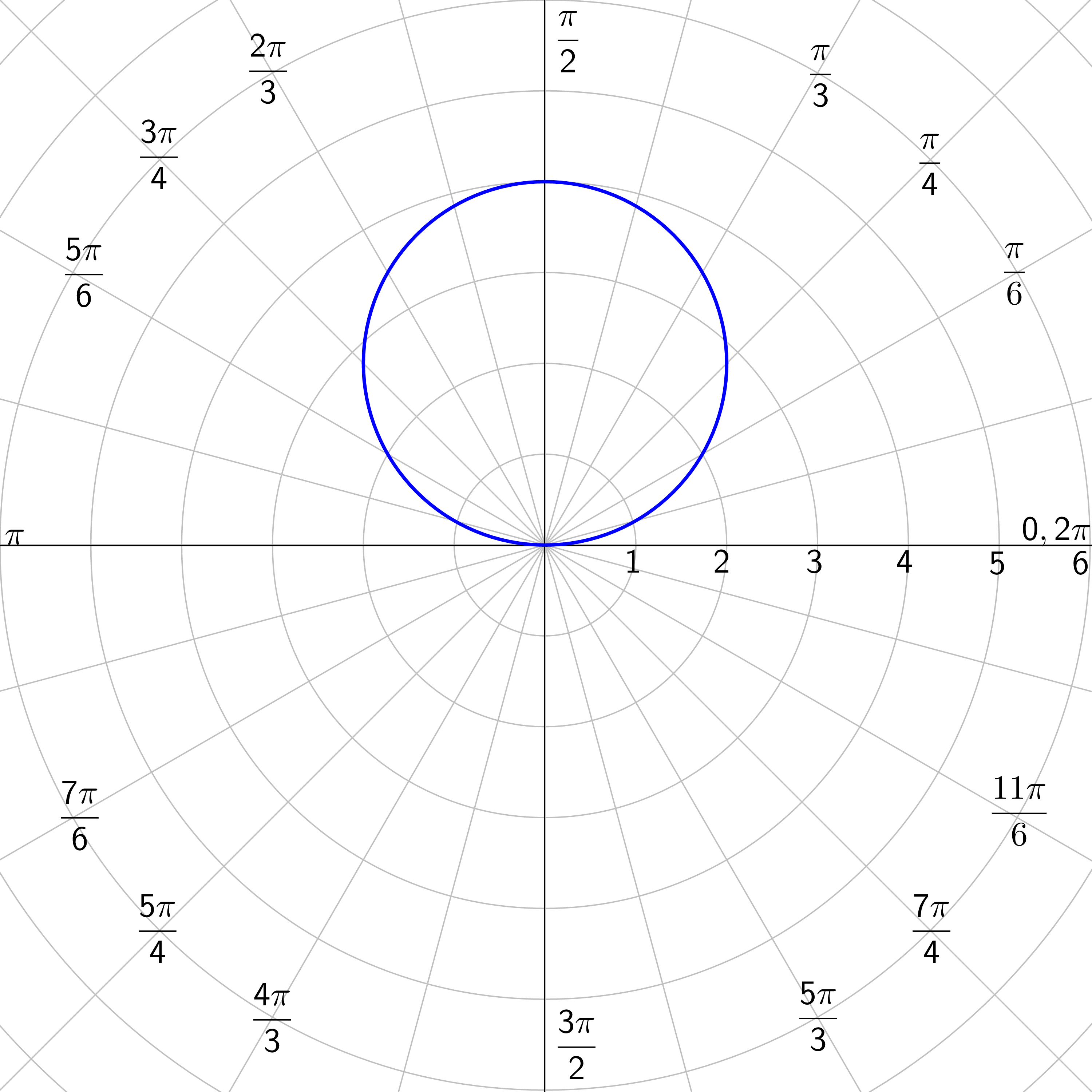
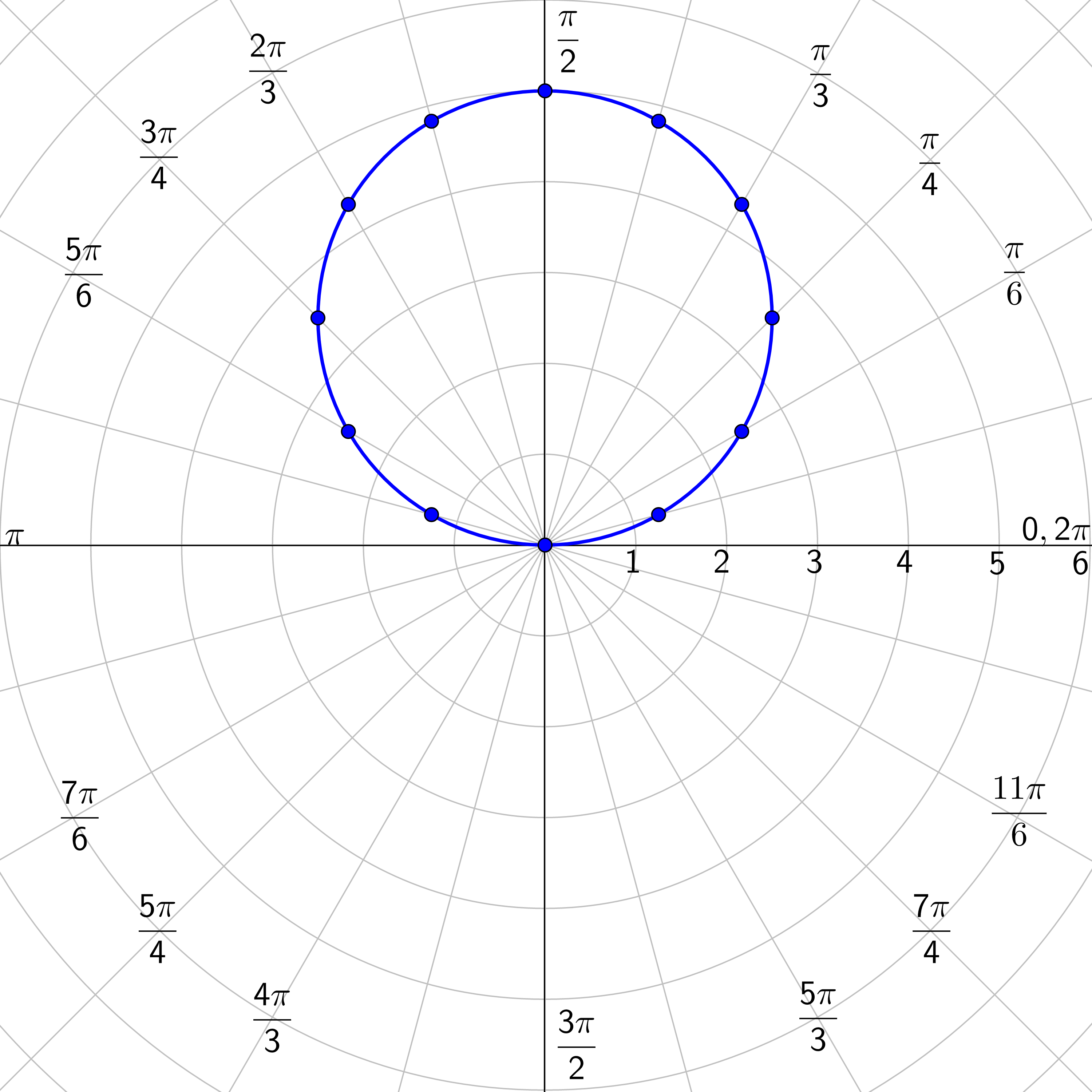
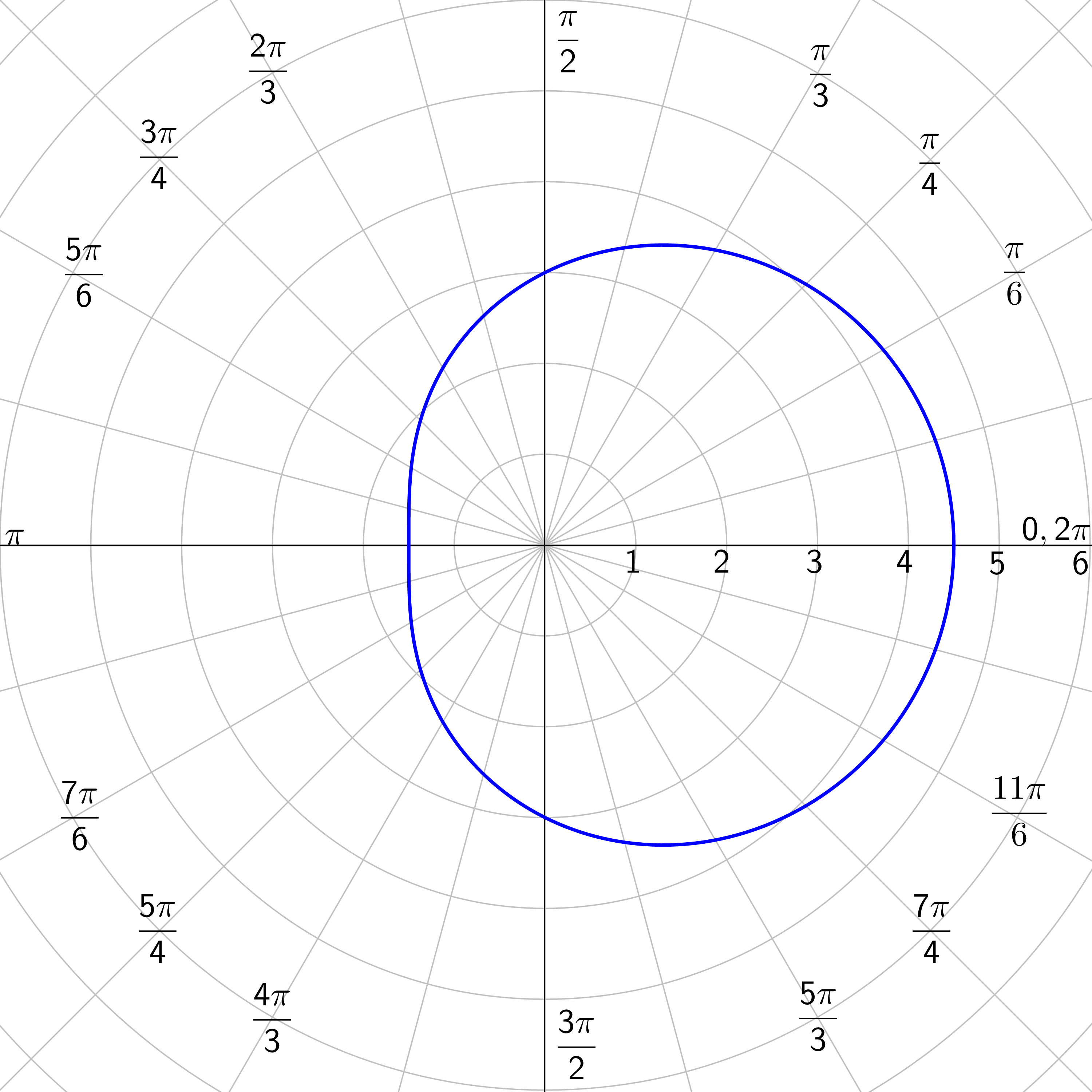
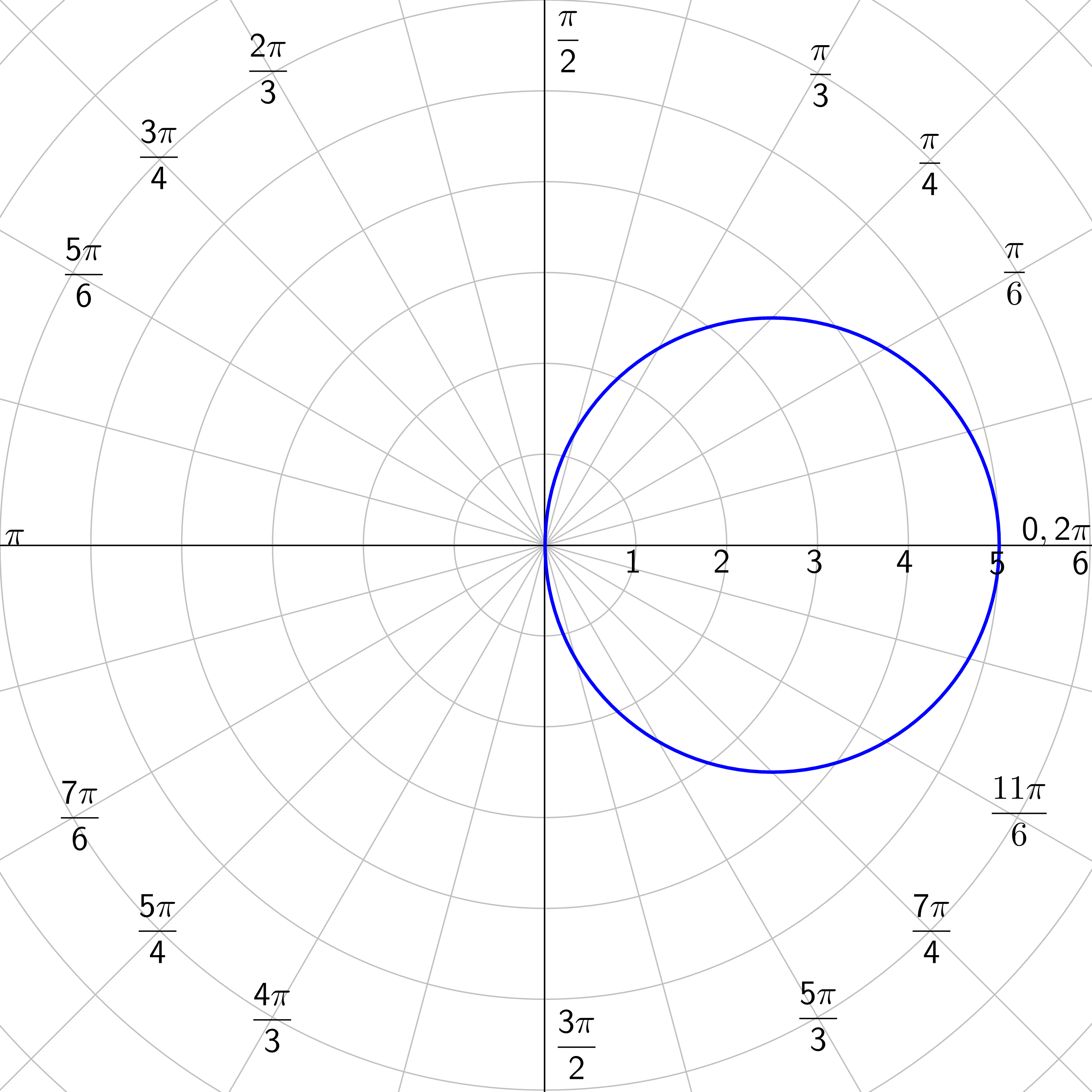
Graph r = 5 sin θ.
Solution
Make a table for r and θ. Choose θ and calculate r.
| r | 0 | 1.3 | 2.5 | 3.5 | 4.3 | 4.8 | 5 | 4.8 | 4.3 | 3.5 | 2.5 | 1.3 | 0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| θ | 0 | \(\frac{π}{12}\) | \(\frac{π}{6}\) | \(\frac{π}{4}\) | \(\frac{π}{3}\) | \(\frac{5π}{12}\) | \(\frac{π}{2}\) | \(\frac{7π}{12}\) | \(\frac{2π}{3}\) | \(\frac{3π}{4}\) | \(\frac{5π}{6}\) | \(\frac{11π}{12}\) | \(π\) |
| r | −1.3 | −2.5 | −3.5 | −4.3 | −4.8 | −5 | −4.8 | −4.3 | −3.5 | −2.5 | −1.3 | 0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| θ | \(\frac{13π}{12}\) | \(\frac{7π}{6}\) | \(\frac{5π}{4}\) | \(\frac{4π}{3}\) | \(\frac{17π}{12}\) | \(\frac{3π}{2}\) | \(\frac{19π}{12}\) | \(\frac{5π}{3}\) | \(\frac{7π}{4}\) | \(\frac{11π}{6}\) | \(\frac{23π}{12}\) | \(2π\) |
Plot all the points and draw a nice curve. This graph is a circle.
Notice that the points in the second table repeated the points in the first table.
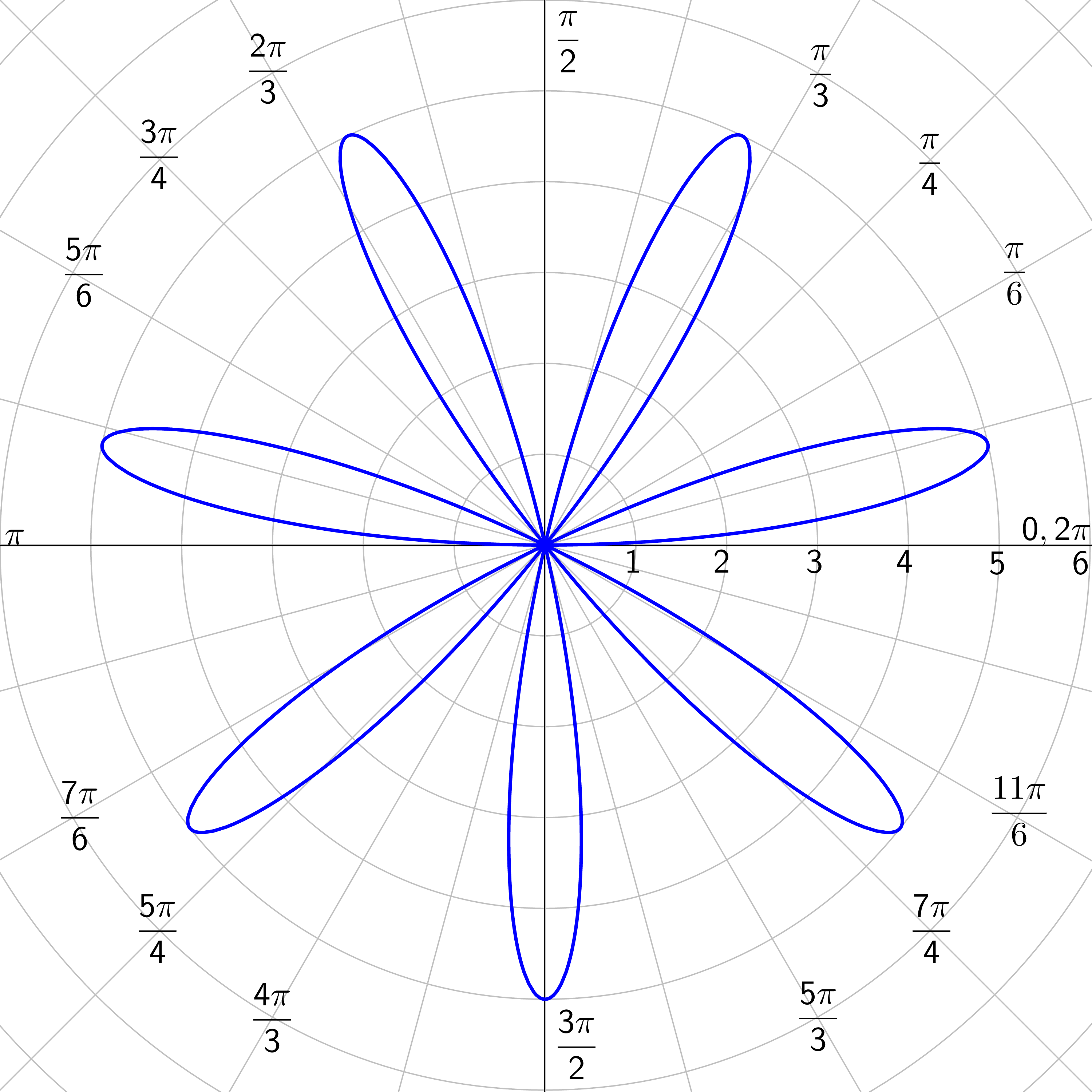
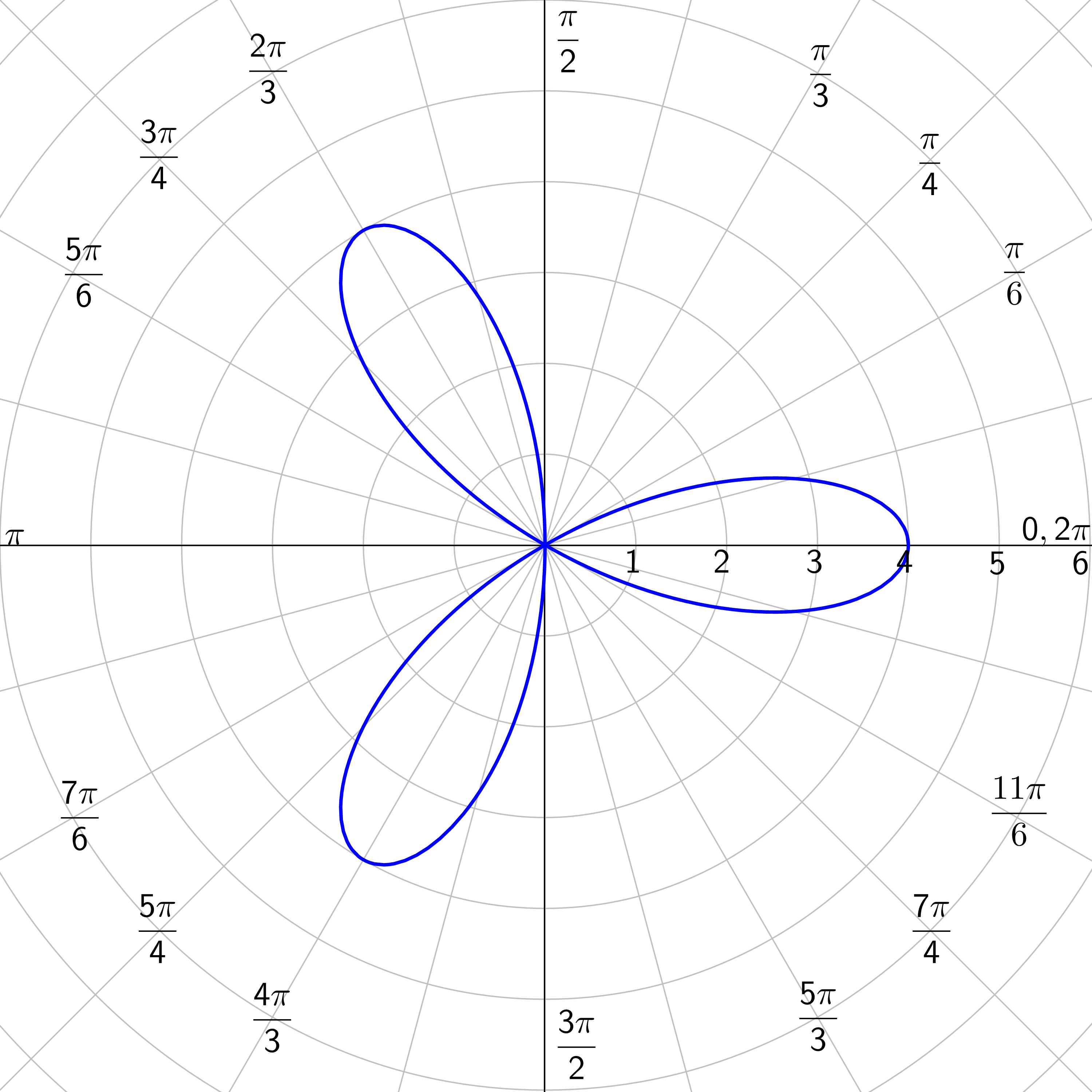
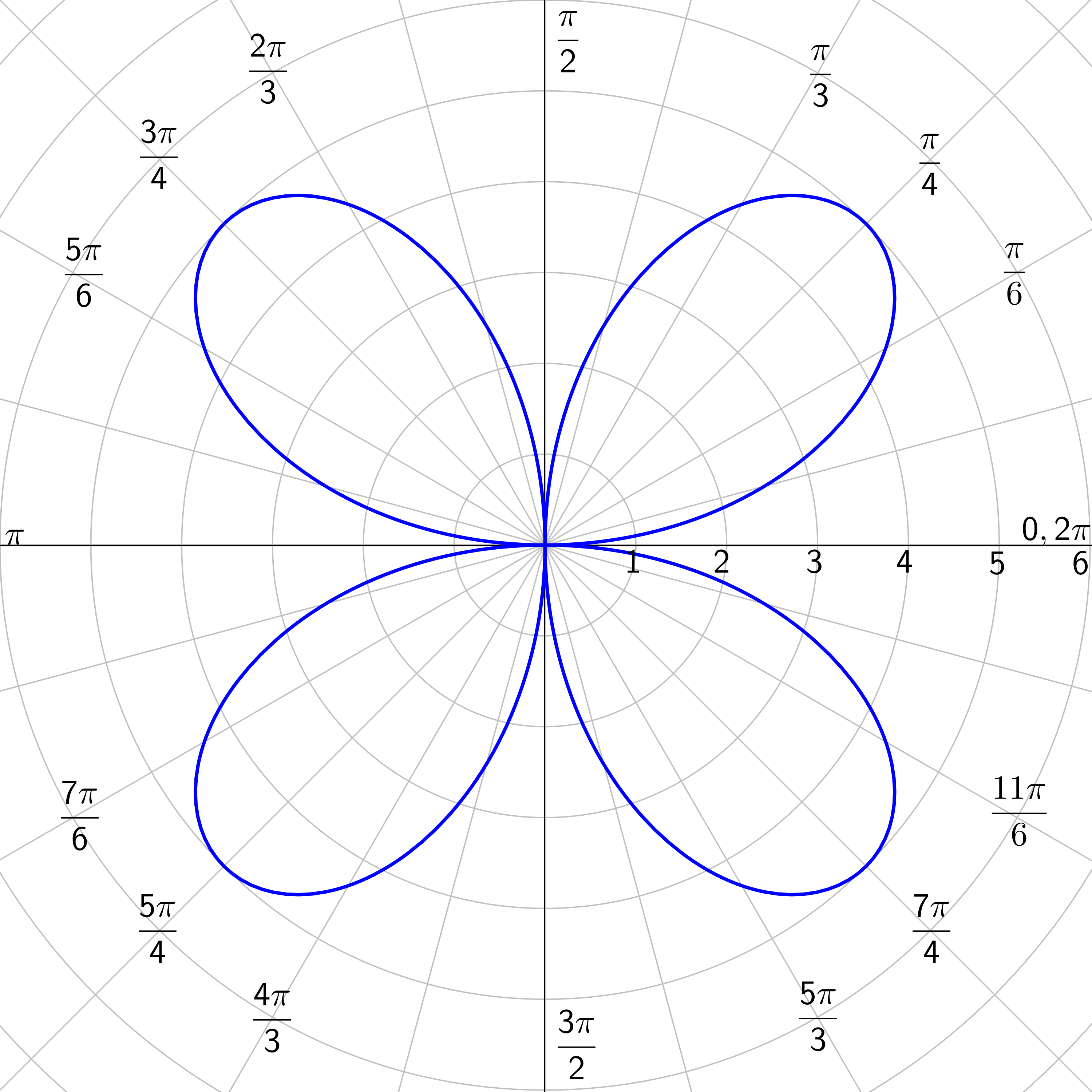
Graph r = 4 cos (3θ).
Answer
Some graphs have symmetry and which makes allows you to use fewer points to make the graph. There are three types of symmetry: line \(θ = \frac{π}{2}\) (y-axis), polar axis (x-axis), and pole (origin). Each of these has a test to determine if a polar equation has that type of symmetry.
A graph has the following type of symmetry if a given substitution into the equation simplifies to the original equation.
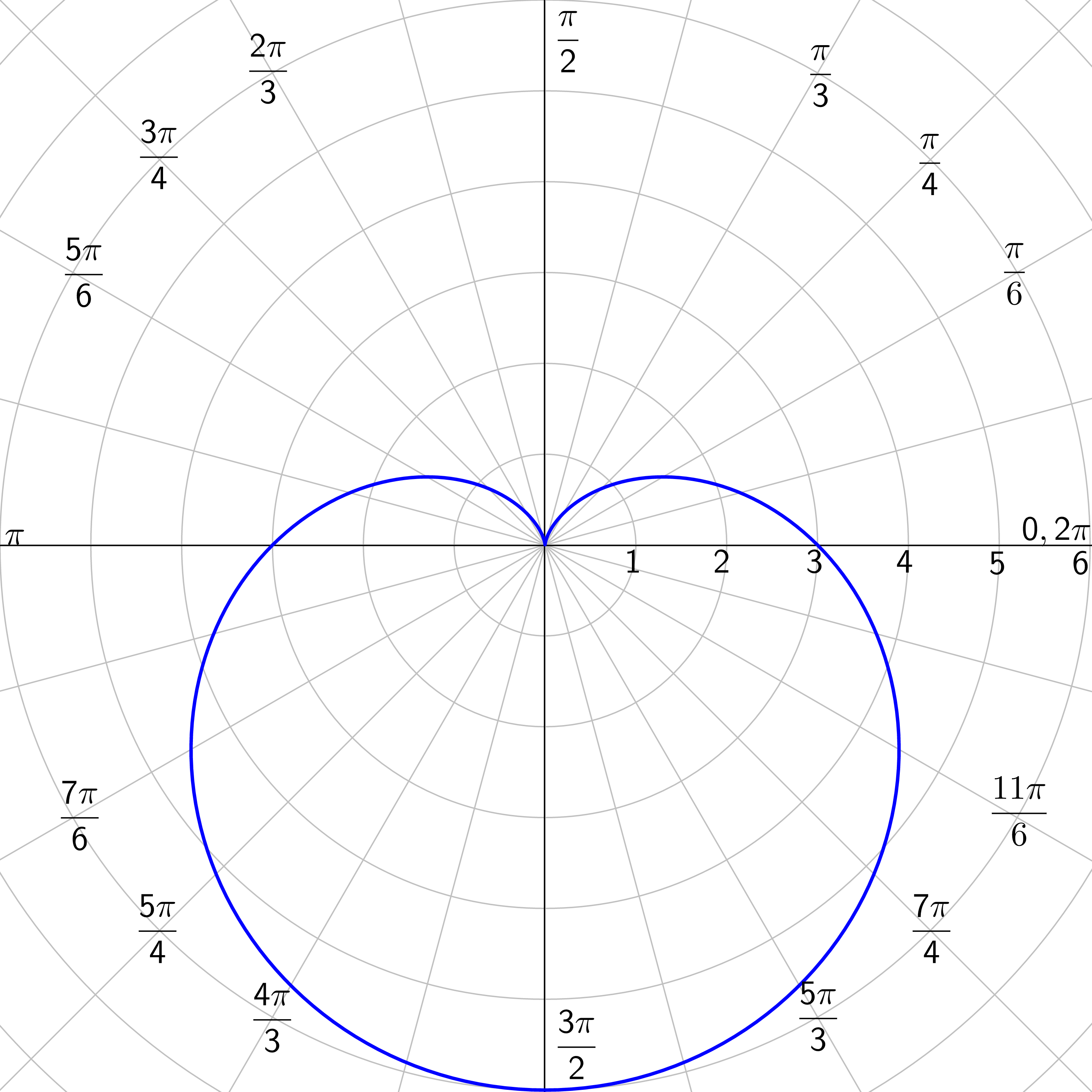
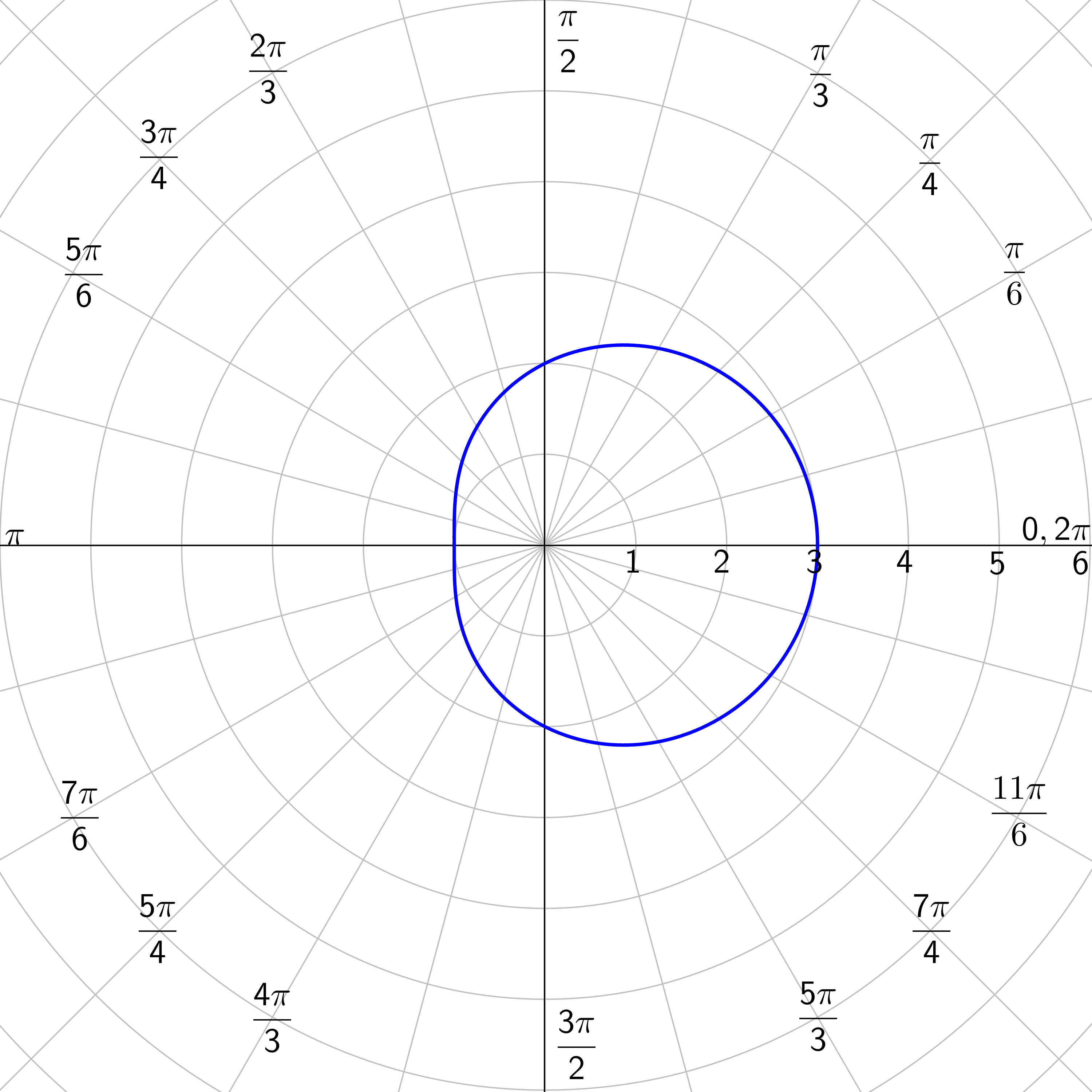
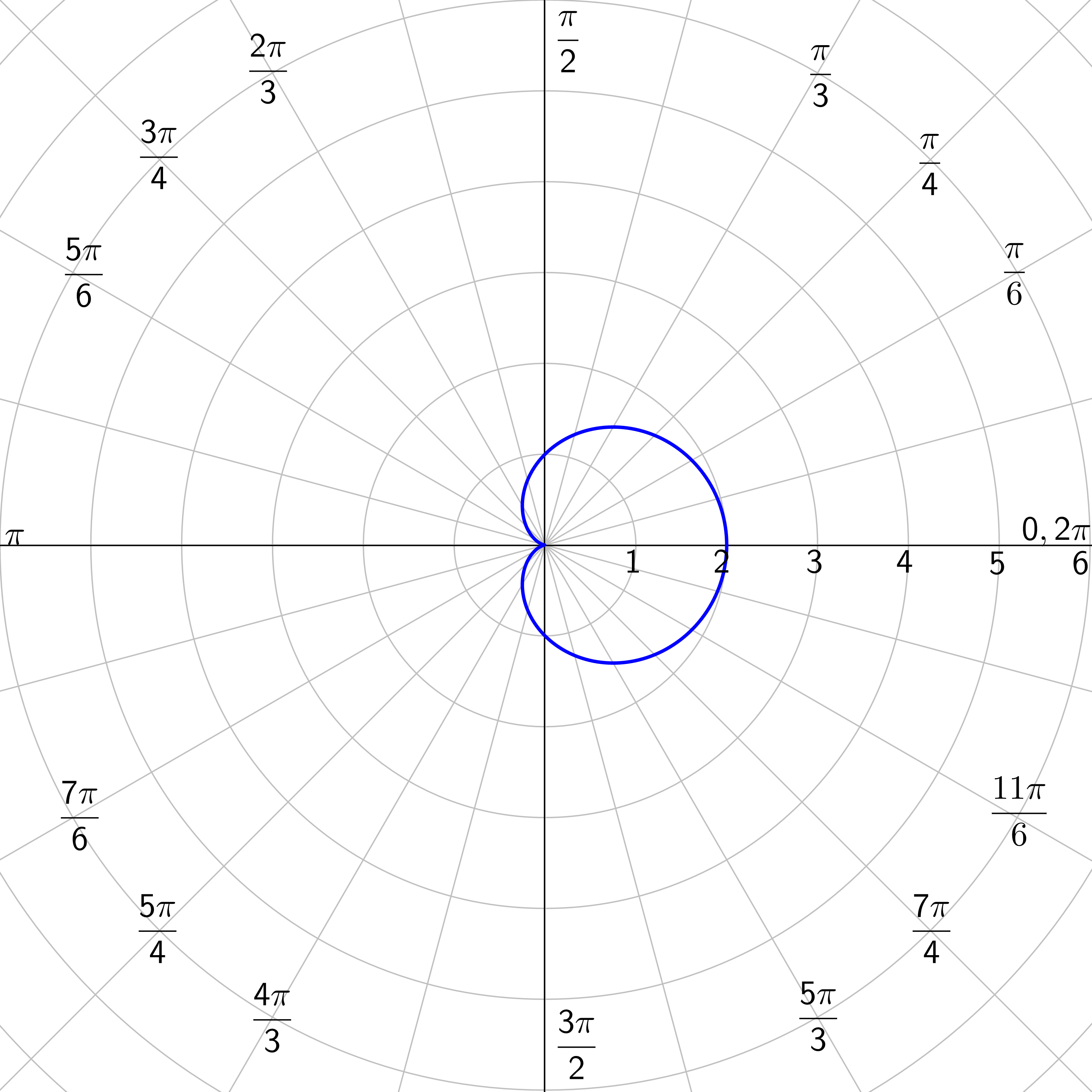
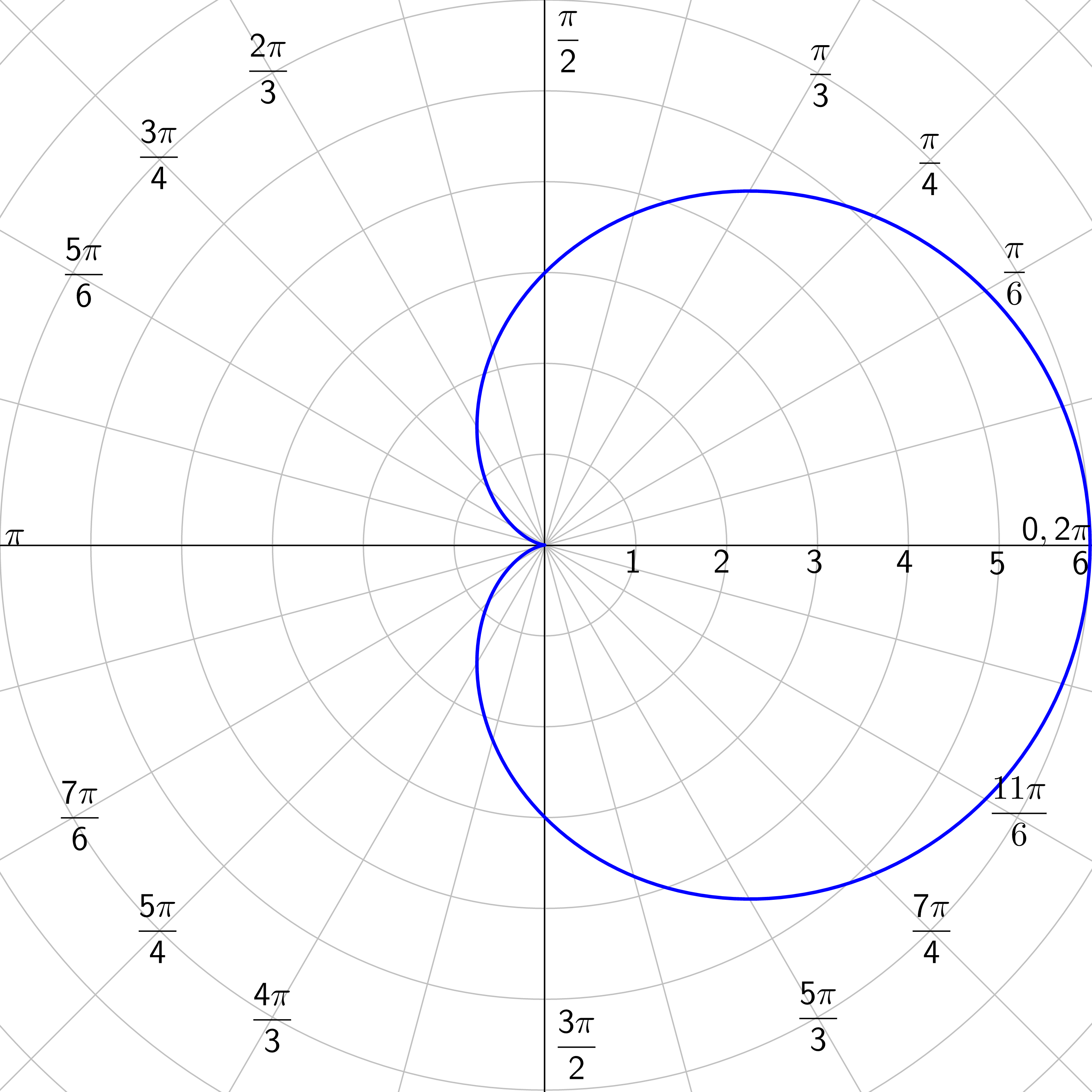
Find the symmetry of r = 3(1 + cos θ).
Solution
Test for symmetry in the line \(θ = \frac{π}{2}\). Substitute (r, π − θ) for (r, θ).
r = 3(1 + cos θ)
r = 3(1 + cos (π − θ))
Use a difference formula (cos(u − v) = cos u cos v + sin u sin v).
r = 3(1 + (cos π cos θ + sin π sin θ))
r = 3(1 + (−cos θ + 0))
r = 3(1 − cos θ)
This is not the same as the original, so it does not have \(θ = \frac{π}{2}\) symmetry.
Test for symmetry in the polar axis. Substitute (r, −θ) for (r, θ).
r = 3(1 + cos θ)
r = 3(1 + cos(−θ))
Use an even/odd identity (cos(−u) = cos u).
r = 3(1 + cos θ)
This is the same as the original, so it does have polar axis symmetry.
Test for symmetry in the pole. Substitute (r, π + θ) for (r, θ).
r = 3(1 + cos θ)
r = 3(1 + cos(π + θ))
Use a sum formula (cos(u + v) = cos u cos v − sin u sin v).
r = 3(1 + (cos π cos θ − sin π sin θ))
r = 3(1 + (−cos θ + 0))
r = 3(1 − cos θ)
This is not the same as the original, so it does not have pole symmetry.
Just because the tests for symmetry do not simplify to the original equation, does not mean that symmetry does not exist. In general, polar equations that are functions of cosine are symmetric over the polar axis and functions of sine are symmetric over the line \(θ = \frac{π}{2}\).
A graph has the following type of symmetry if a given substitution into the equation simplifies to the original equation.
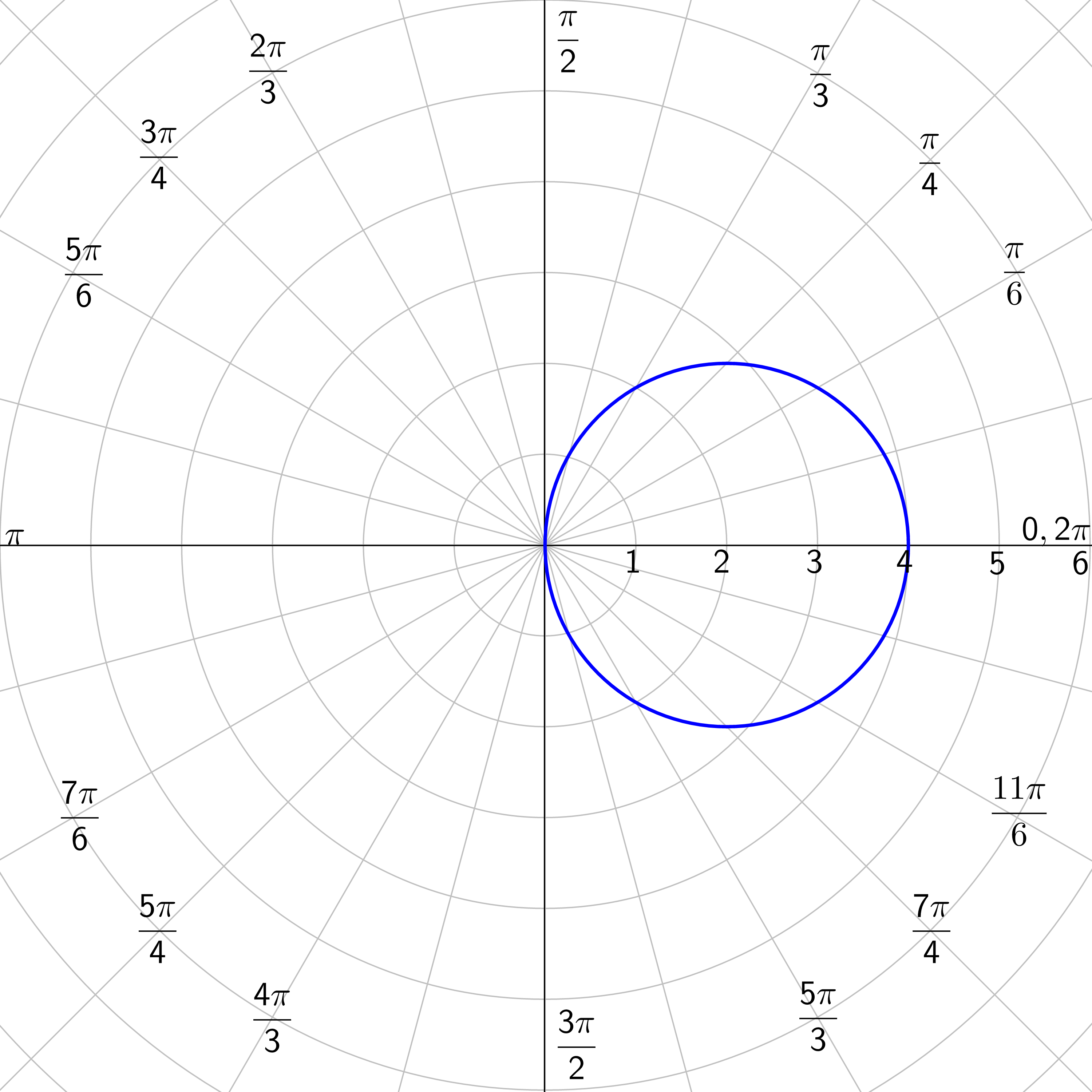
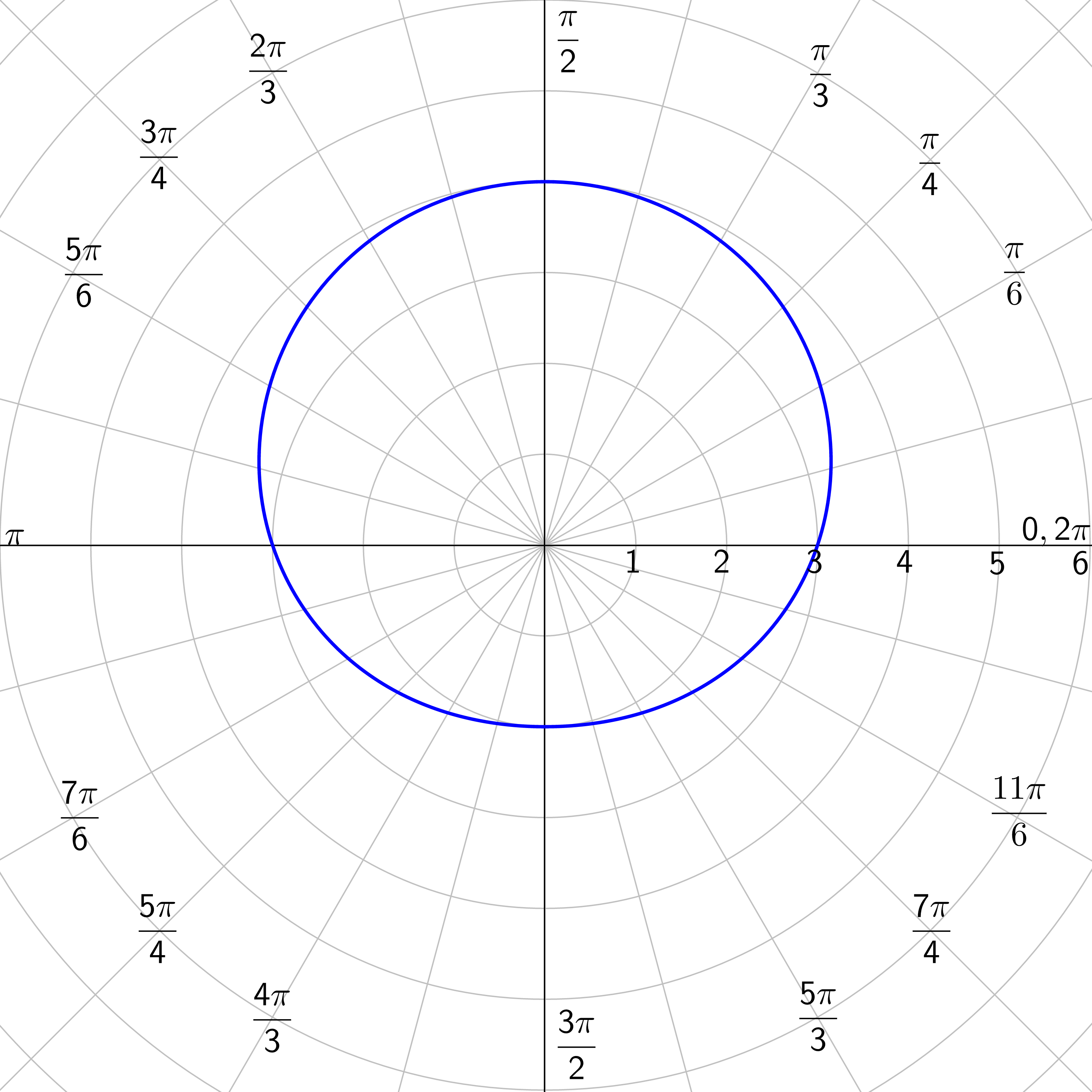
Find the symmetry of r = 3 + sin(θ).
Answer
This is a function of sine, so line \(θ = \frac{π}{2}\). Also, it passes only the symmetry test for the line \(θ = \frac{π}{2}\).
Maximums of polar equations occur when |r| is at its largest. These are locations where the graph is farthest from the pole. Zeros occur when r = 0. These are locations where the graph is at the pole. Both maximums and zeros are found by looking for when the trigonometric portion of the equation is at a maximum or zero.
Find the maximums and zeros of r = 3 sin 2θ.
Solution
Maximums
The trigonometric portion is sin 2θ. Find the angles where it is at a maximum. The largest values of sine is 1 and −1.
sin 2θ = 1 when \(2θ = \frac{π}{2} + 2πn\)
sin 2θ = −1 when \(2θ = \frac{3π}{2} + 2πn\)
Divide both by 2.
$$ θ = \frac{π}{4} + πn\text{ and }\frac{3π}{4} + πn $$
Plug in numbers for n until they reach 2π.
$$ θ = \frac{π}{4}, \frac{3π}{4}, \frac{5π}{4}, \frac{7π}{4} $$
Zeros
Let r = 0 and solve for θ.
0 = 3 sin 2θ
0 = sin 2θ
2θ = 0 + πn
$$ θ = \frac{π}{2}n $$
$$ θ = 0, \frac{π}{2}, π, \frac{3π}{2} $$
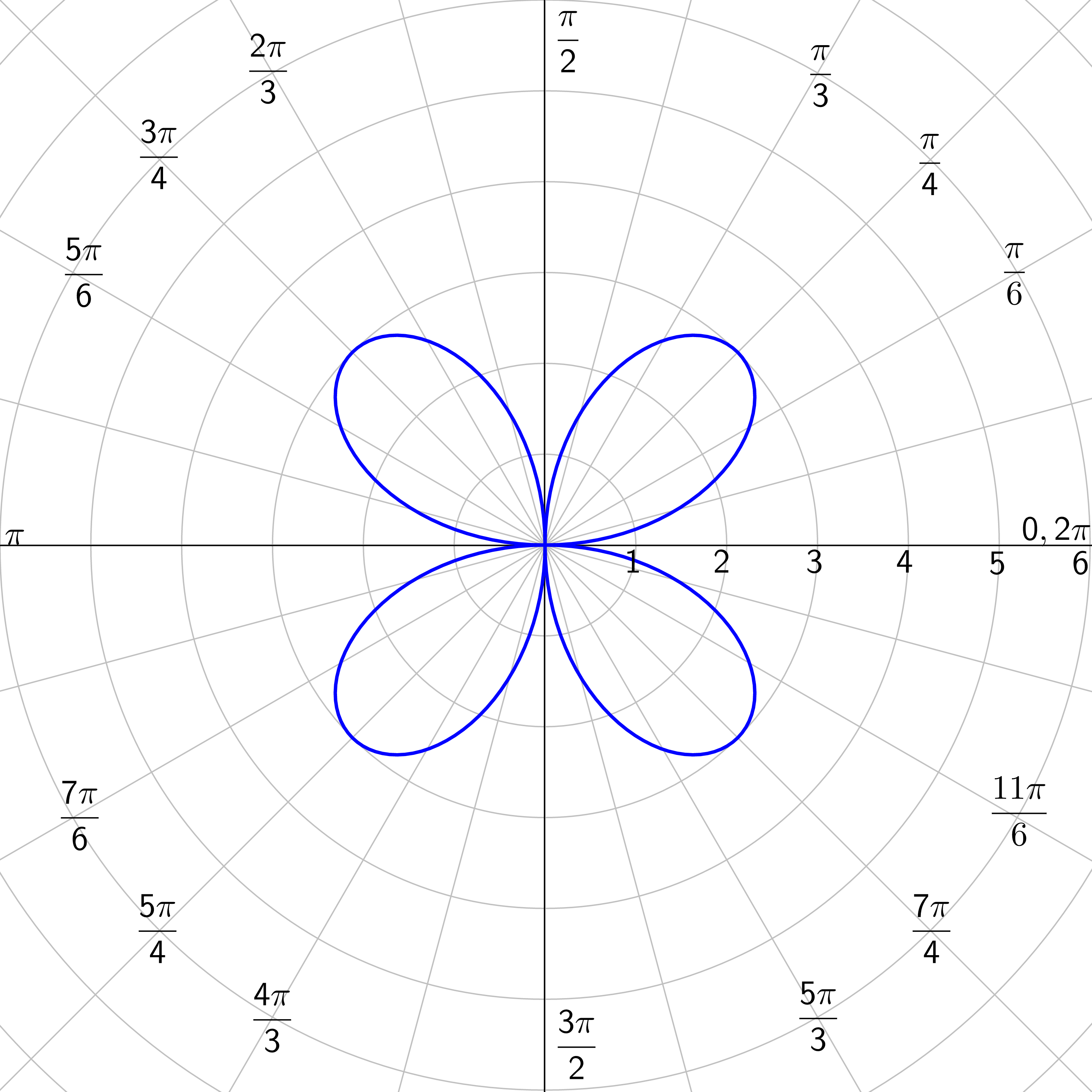
Find the maximums and zeros of r = 5 cos 3θ.
Answer
Maximums: \(θ = 0, \frac{π}{3}, \frac{2π}{3}, π, \frac{4π}{3}, \frac{5π}{3}\); Zeros: \(θ = \frac{π}{6}, \frac{π}{2}, \frac{5π}{6}, \frac{7π}{6}, \frac{3π}{2}, \frac{11π}{6}\)
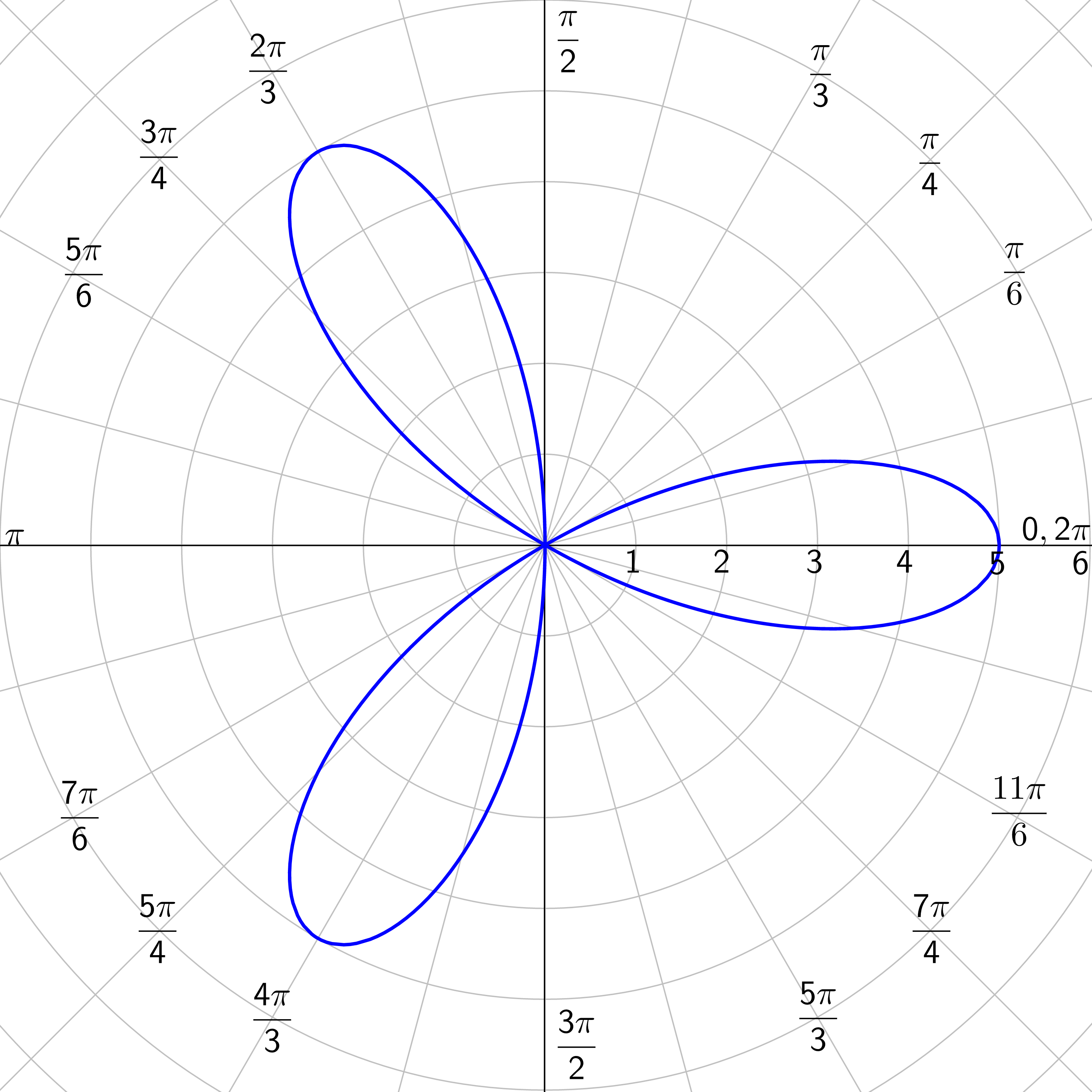
There are several special polar graphs. These are fairly simple in polar form, but very complicated in rectangular form.
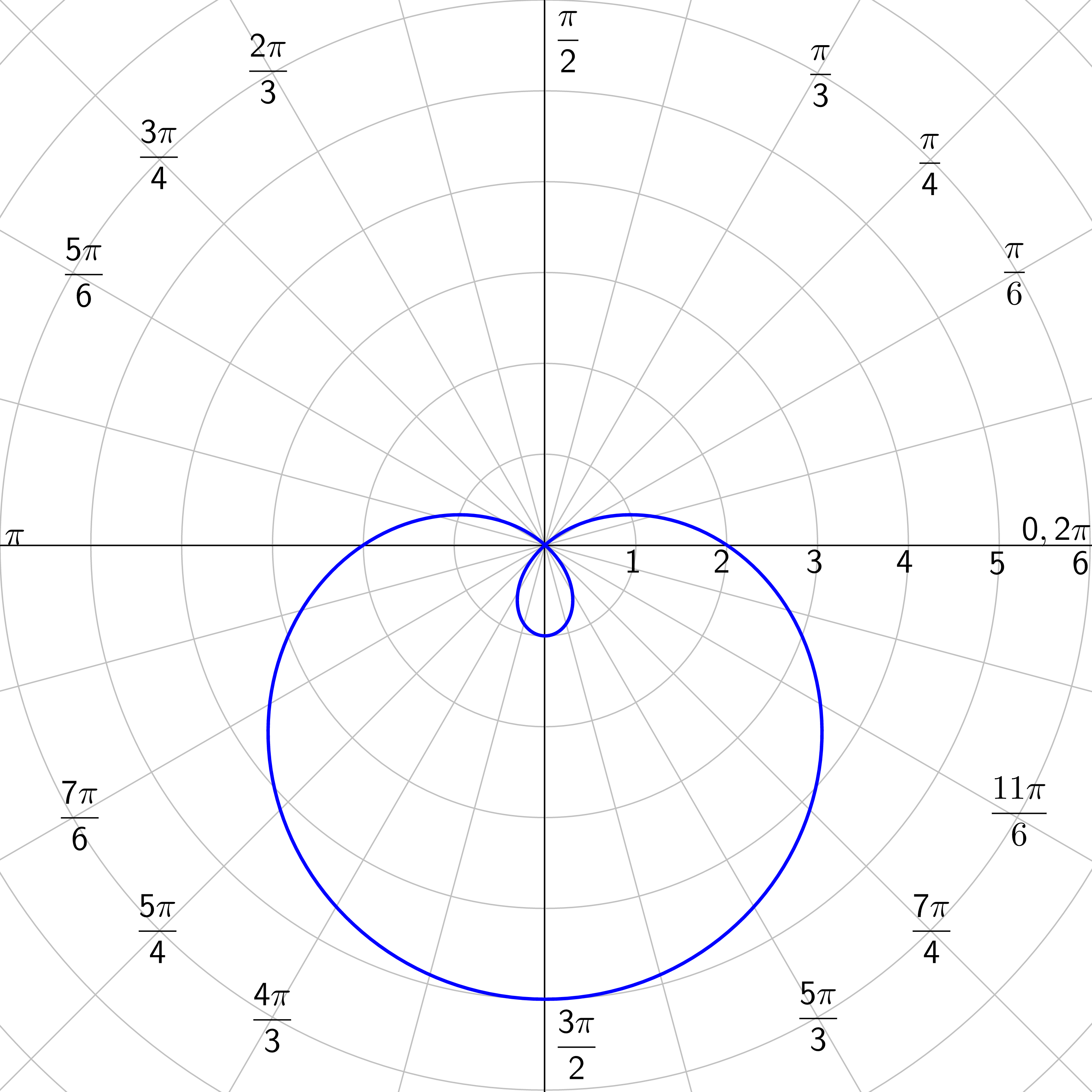
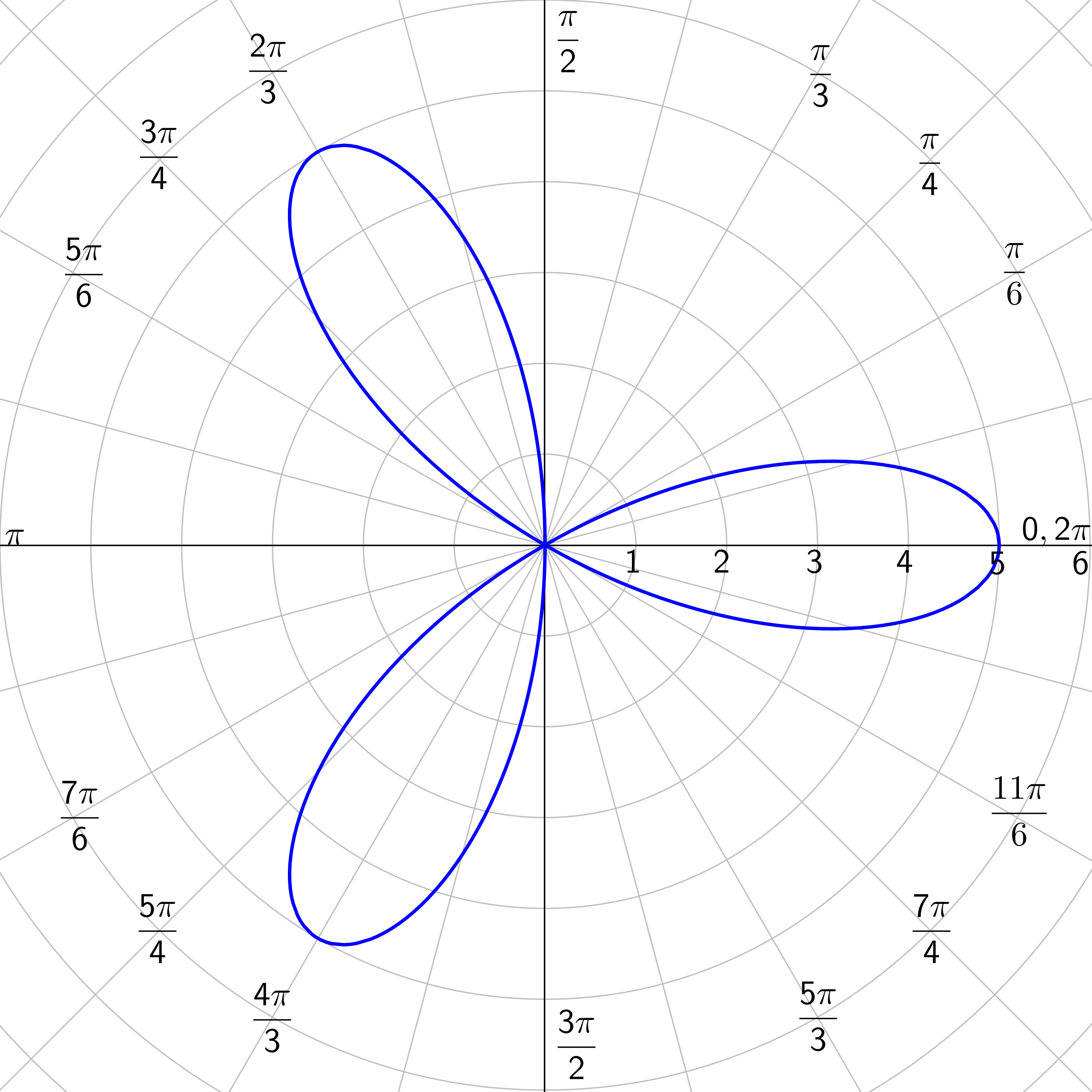
Limaçons: r = a ± b cos θ or r = a ± b sin θ where a > 0 and b > 0.
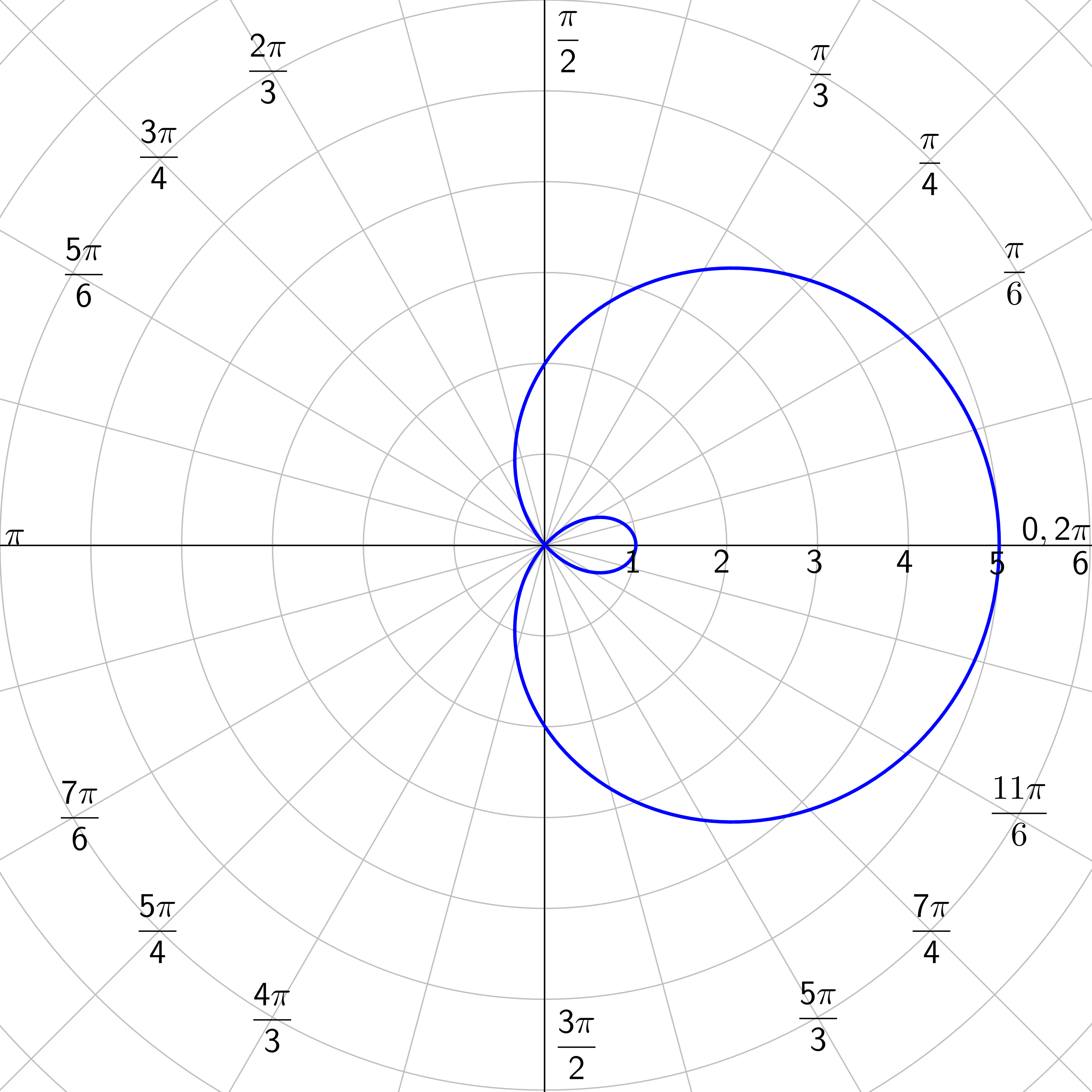
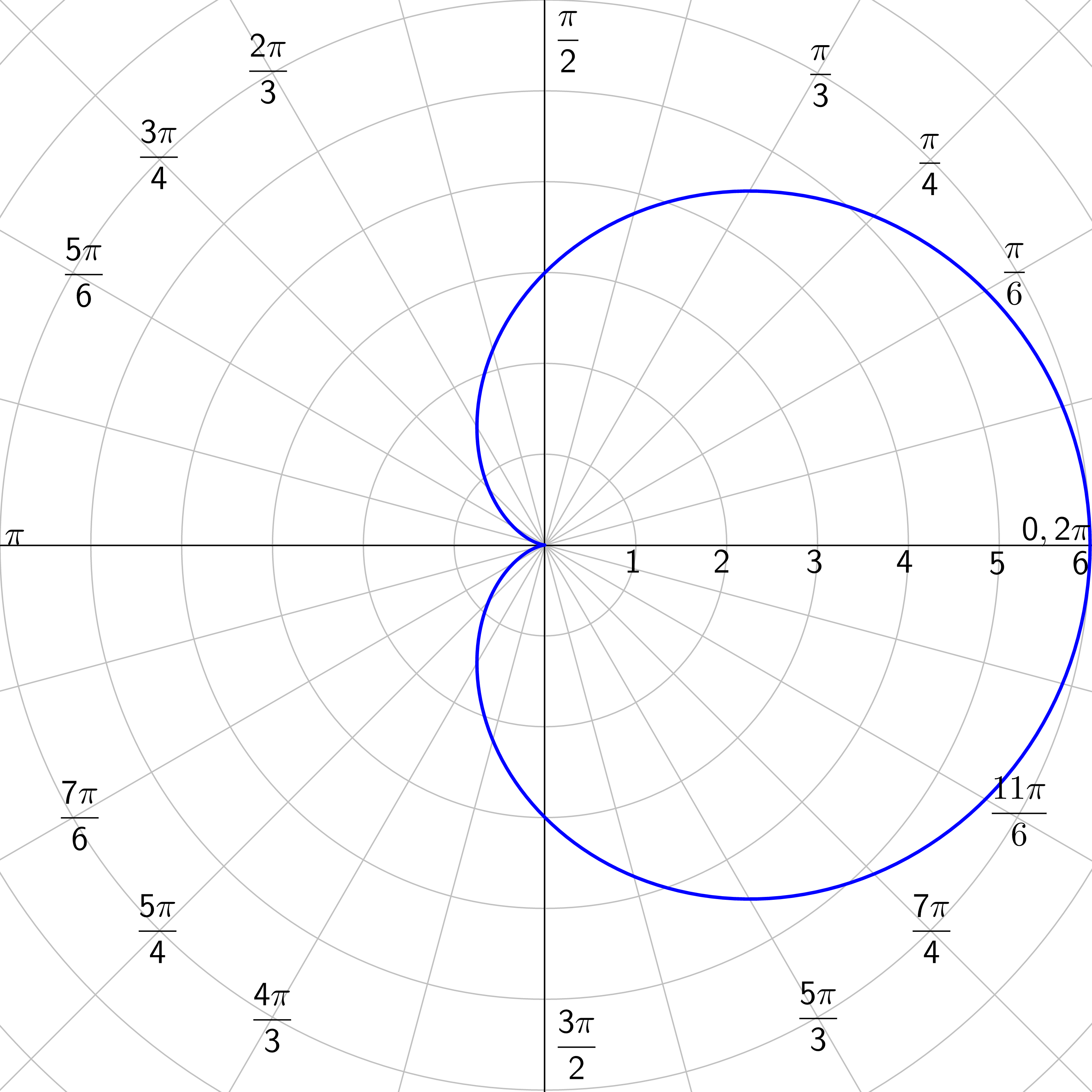
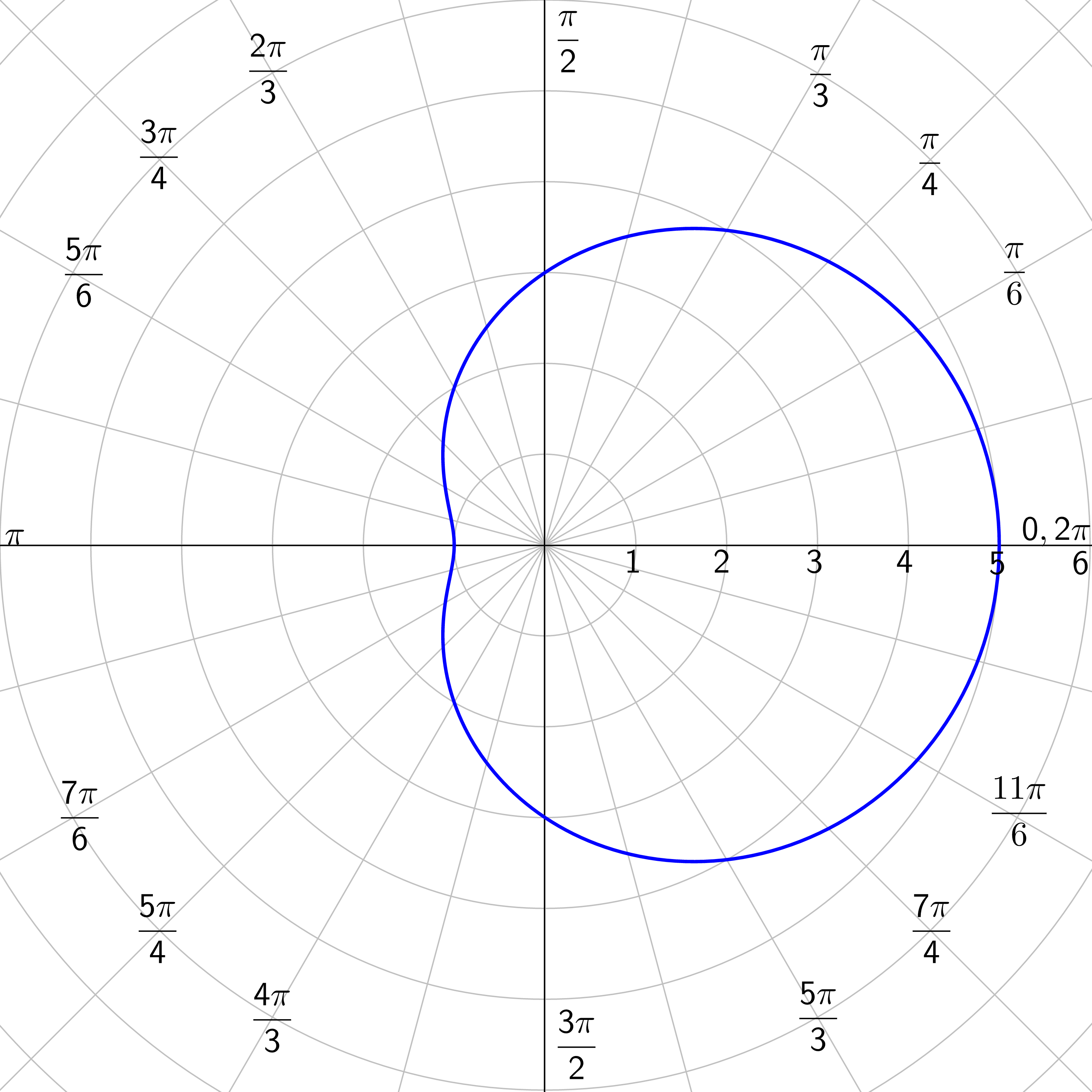
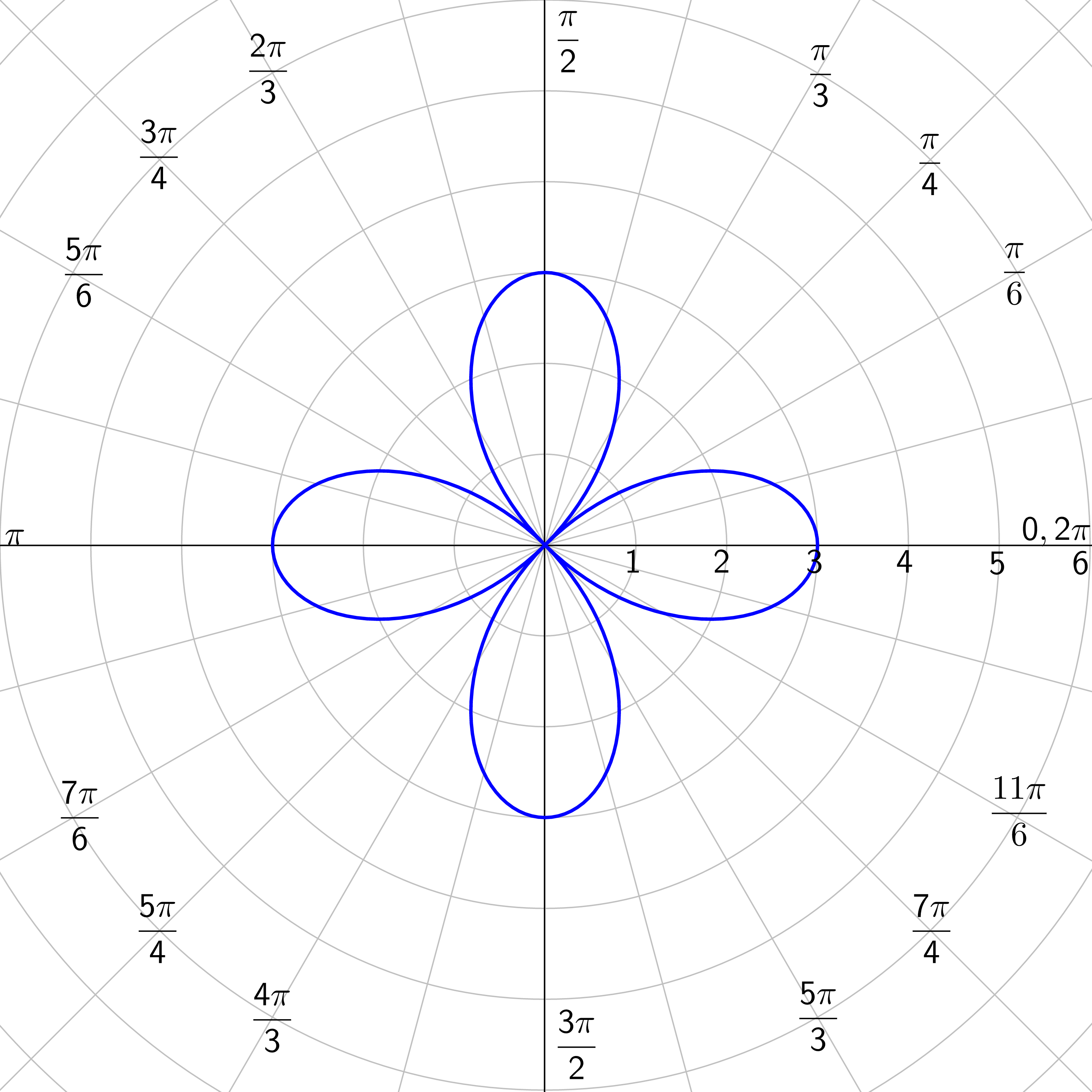
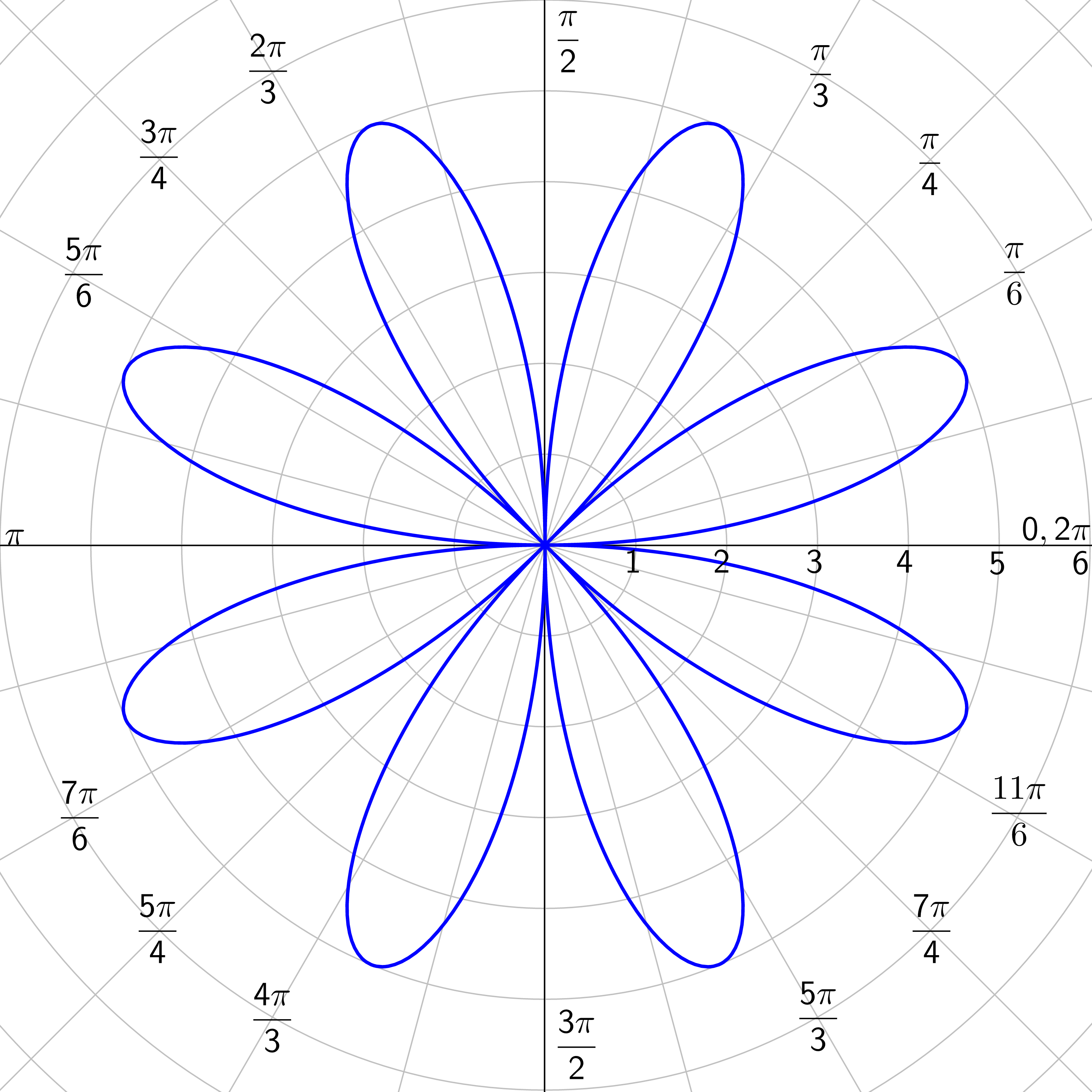
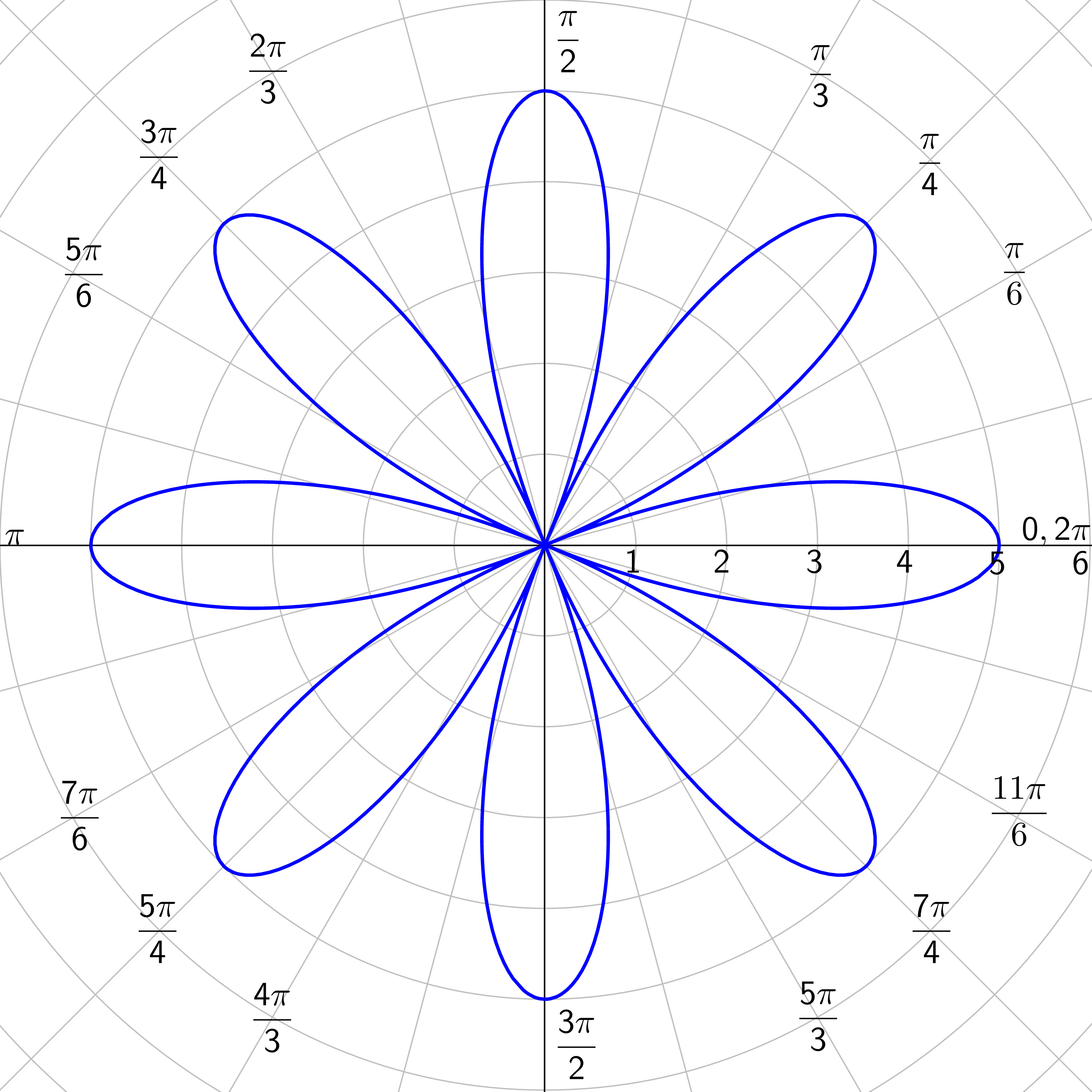
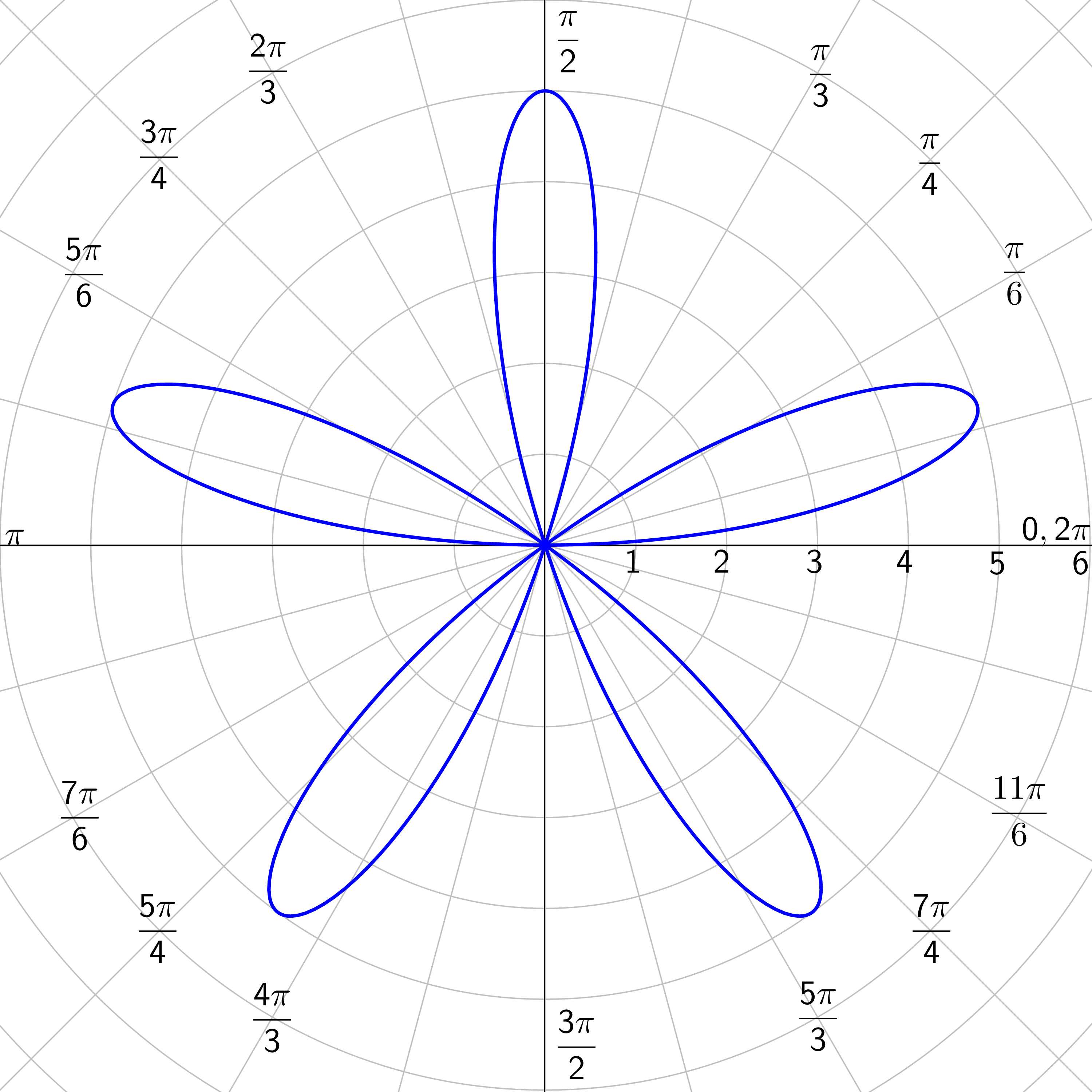
Rose Curves: n petals if n is odd; 2n petals if n is even; n ≥ 2
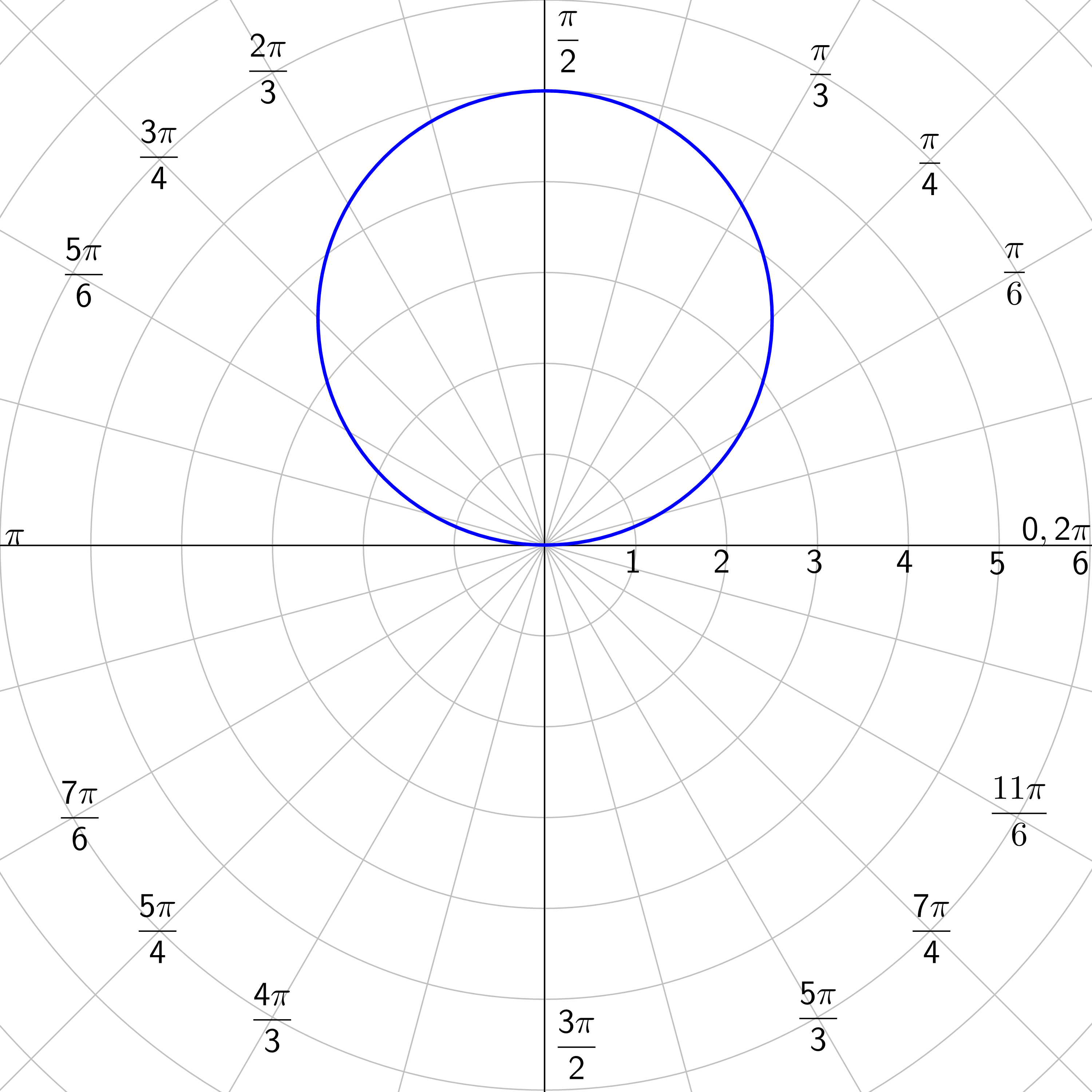
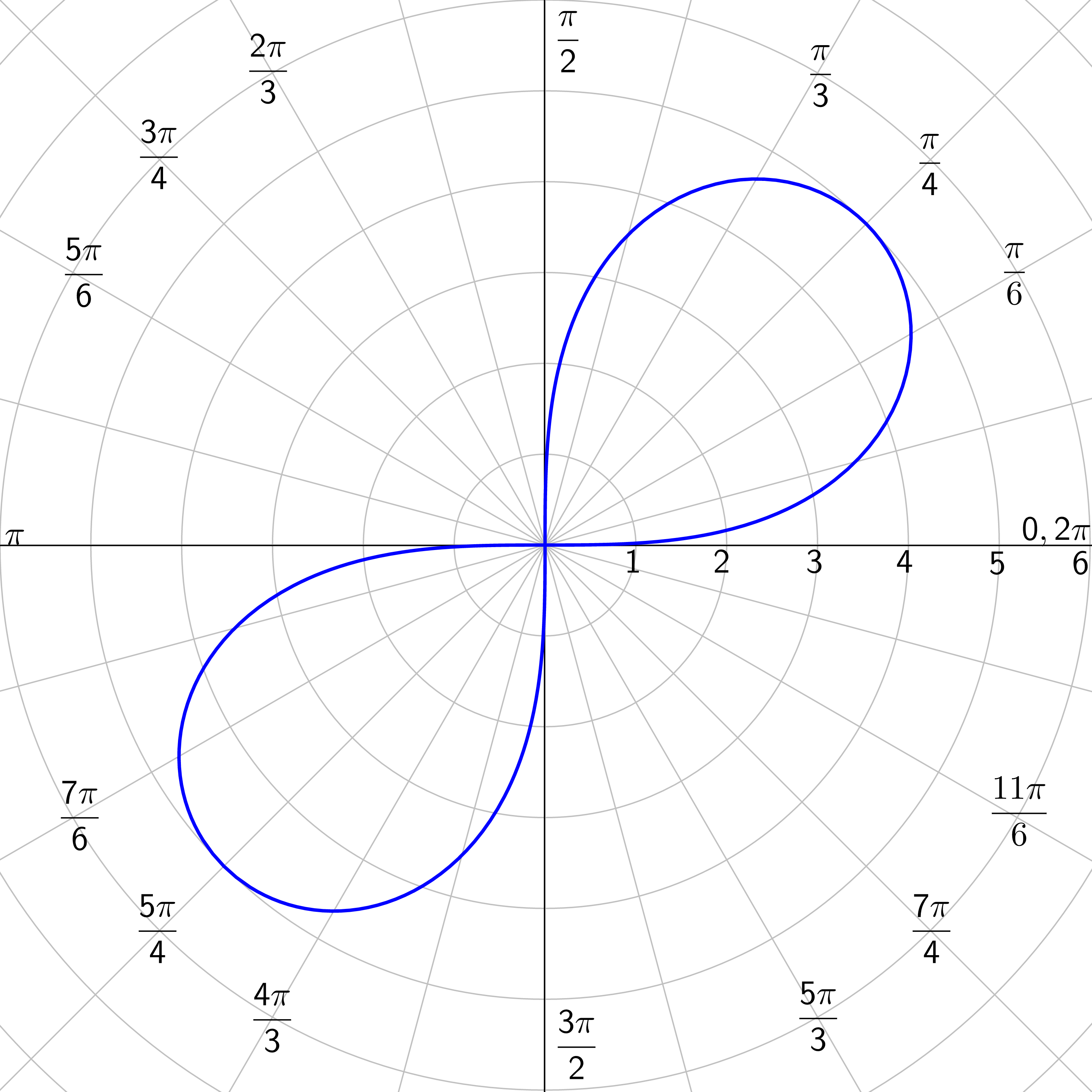
Circles and Lemniscates:
A graph has the following type of symmetry if a given substitution into the equation simplifies to the original equation.
A graph has the following type of symmetry if a given substitution into the equation simplifies to the original equation.
Helpful videos about this lesson.
