Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
I am the vine; you are the branches. If you remain in me and I in you, you will bear much fruit; apart from me you can do nothing. John 15:5 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.5.2
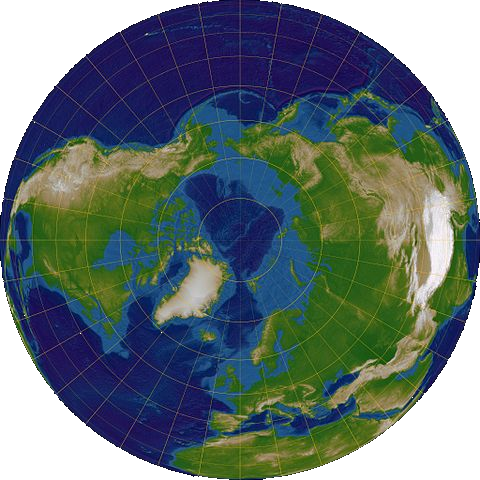
The picture is of the Earth from above the north pole. We are used to seeing the Earth projected as a rectangular map, but it is round. A round map would make more sense. On the figure, the lines of longitude all radiate out from the north pole. Any point in the northern hemisphere can be plotted by knowing which line of longitude the point is on and how far from the north pole the point is.
This chapter is all about conic sections which are constant curves and not straight lines. Rectangular coordinates are convenient and powerful, but why use rectangles to graph curves and circles? It might be more convenient to use circles to graph them. So, this lesson introduces polar coordinates so that circles are used to graph circles.
Polar coordinates give the location of a point as if it was on a circle as (r, θ). The angle variable, θ, tells the angle the a radius through the point is from the polar axis. The polar axis is the same as the positive x-axis in rectangular coordinates. The radius variable, r, tells how far along the radius the point is, or how far the point is from the origin or pole.
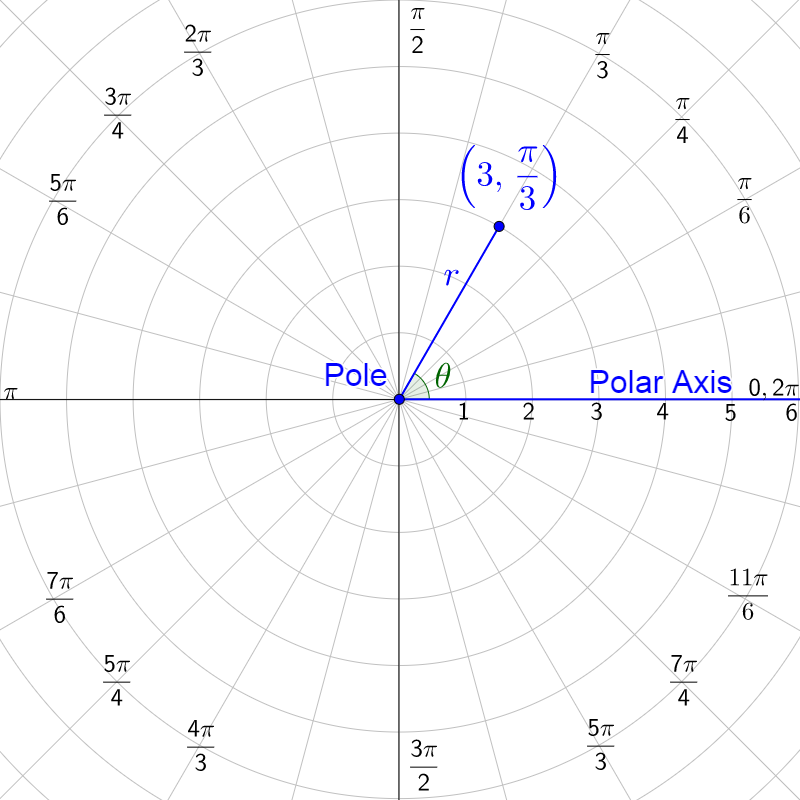
(r, θ)
r = distance from pole
θ = angle counterclockwise from the polar axis
Graph by finding the line for the angle and moving along that line, the distance, r, from the pole.
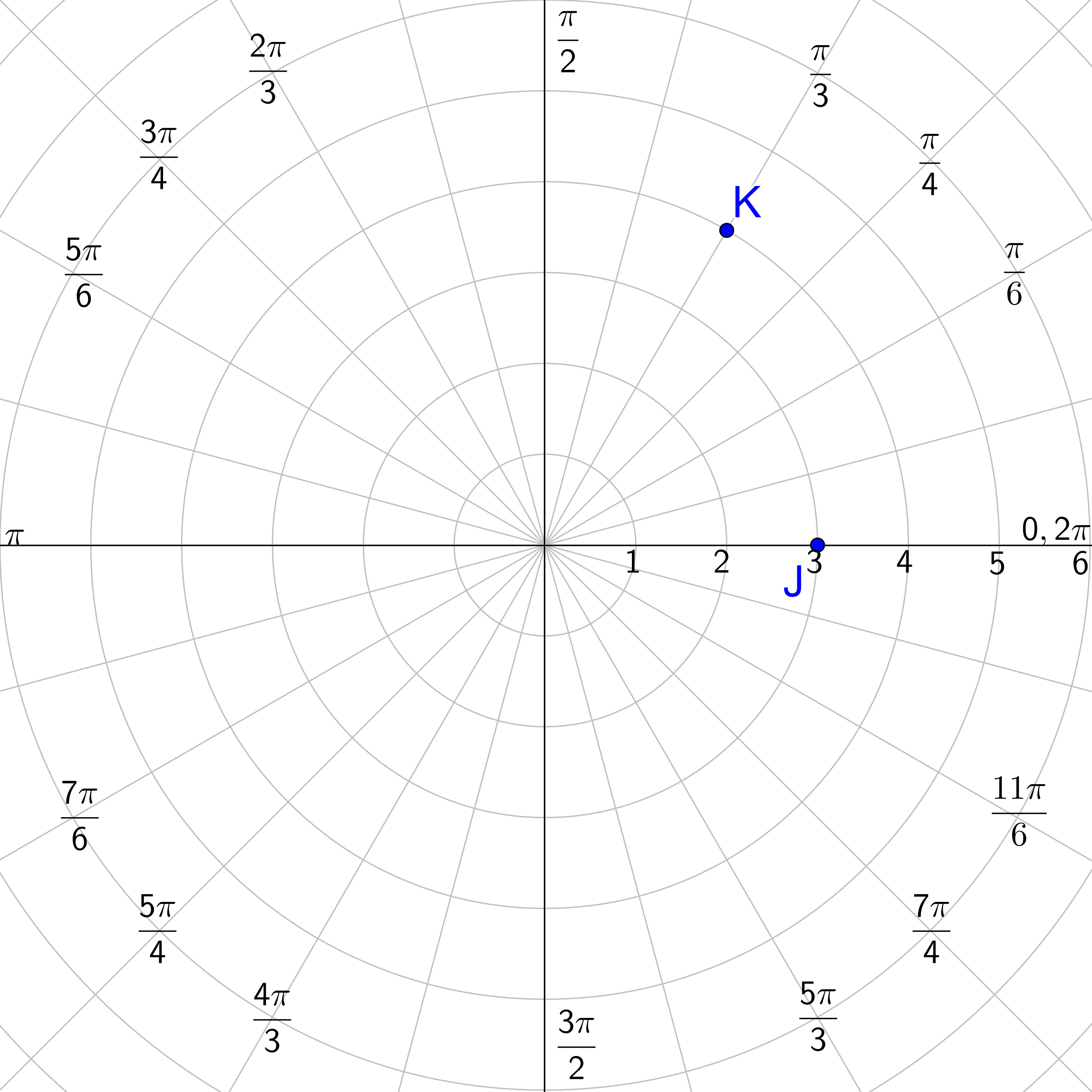
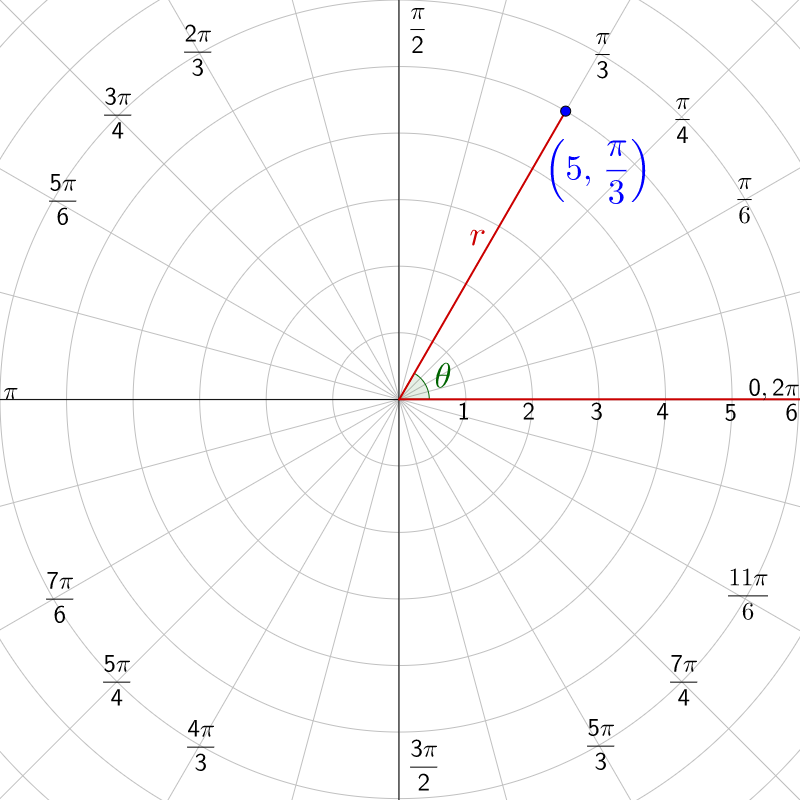
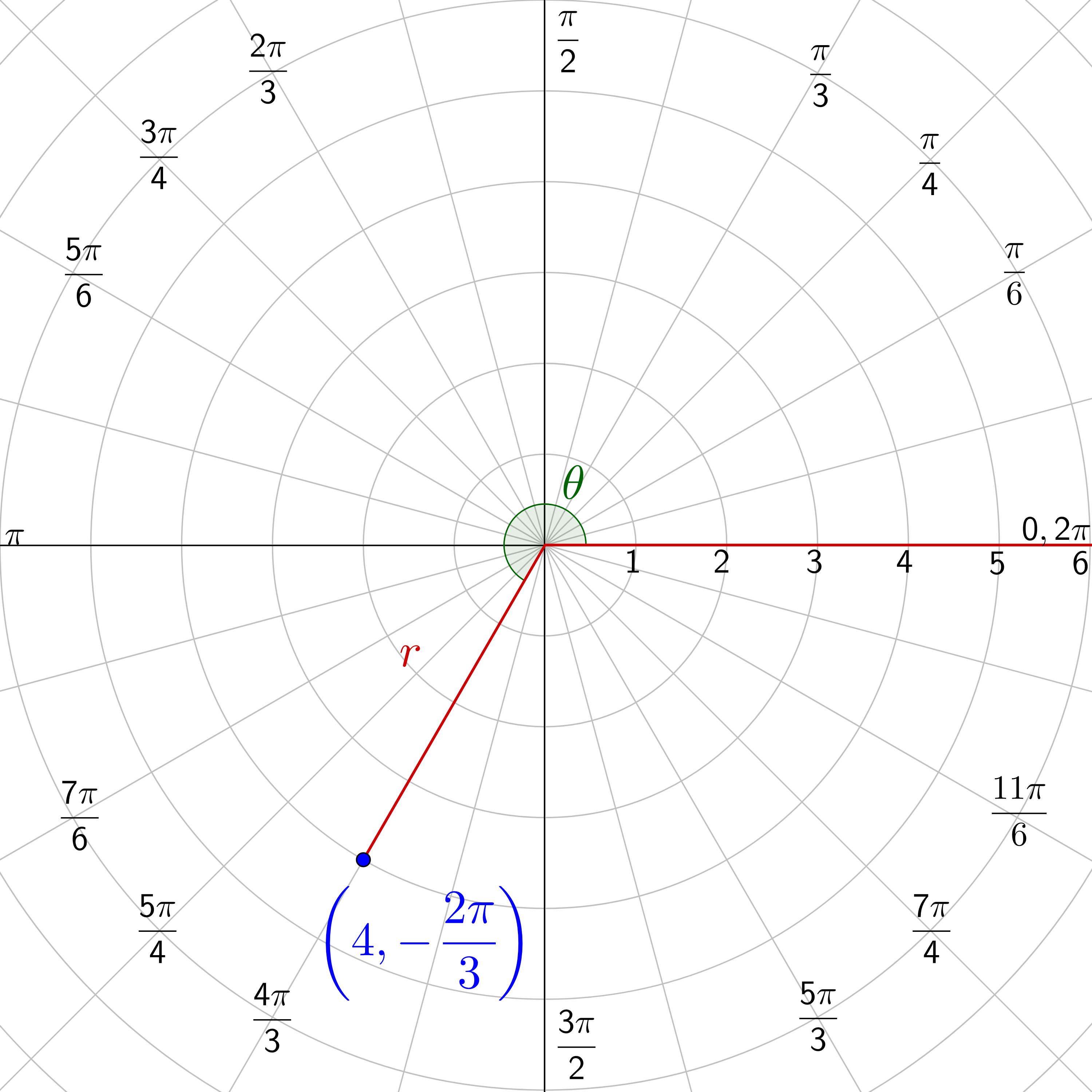
Graph a. \(\left(5, \frac{\pi}{3}\right)\) b. \(\left(-3, \frac{\pi}{2}\right)\) c. \(\left(4, -\frac{2\pi}{3}\right)\).
Solutions
\(\left(5, \frac{\pi}{3}\right)\)
The angle is \(\frac{\pi}{3}\). Find that angle on the graph. The r is 5, so move 5 spaces out from the pole along the \(\frac{\pi}{3}\) line.
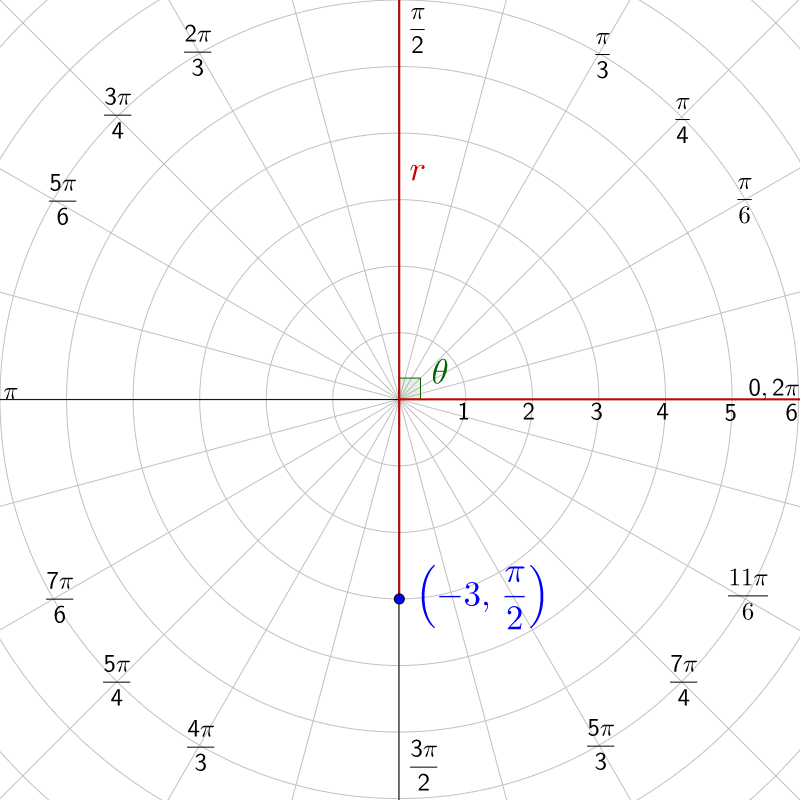
\(\left(-3, \frac{\pi}{2}\right)\)
The angle is \(\frac{\pi}{2}\). Find that angle on the graph. The r is −3, so move 3 spaces backwards from the pole along the \(\frac{\pi}{2}\) line.
\(\left(4, -\frac{2\pi}{3}\right)\)
The angle is \(-\frac{2\pi}{3}\). That is not on the graph, so find a coterminal angle by adding one complete circle, 2π, to the angle.
\(θ = -\frac{2\pi}{3} + 2\pi\)
\(θ = -\frac{2\pi}{3} + \frac{6\pi}{3}\)
\(θ = \frac{4π}{3}\)
Find that angle on the graph. The r is 4, so move 4 spaces out from the pole along the \(\frac{4\pi}{3}\) line.
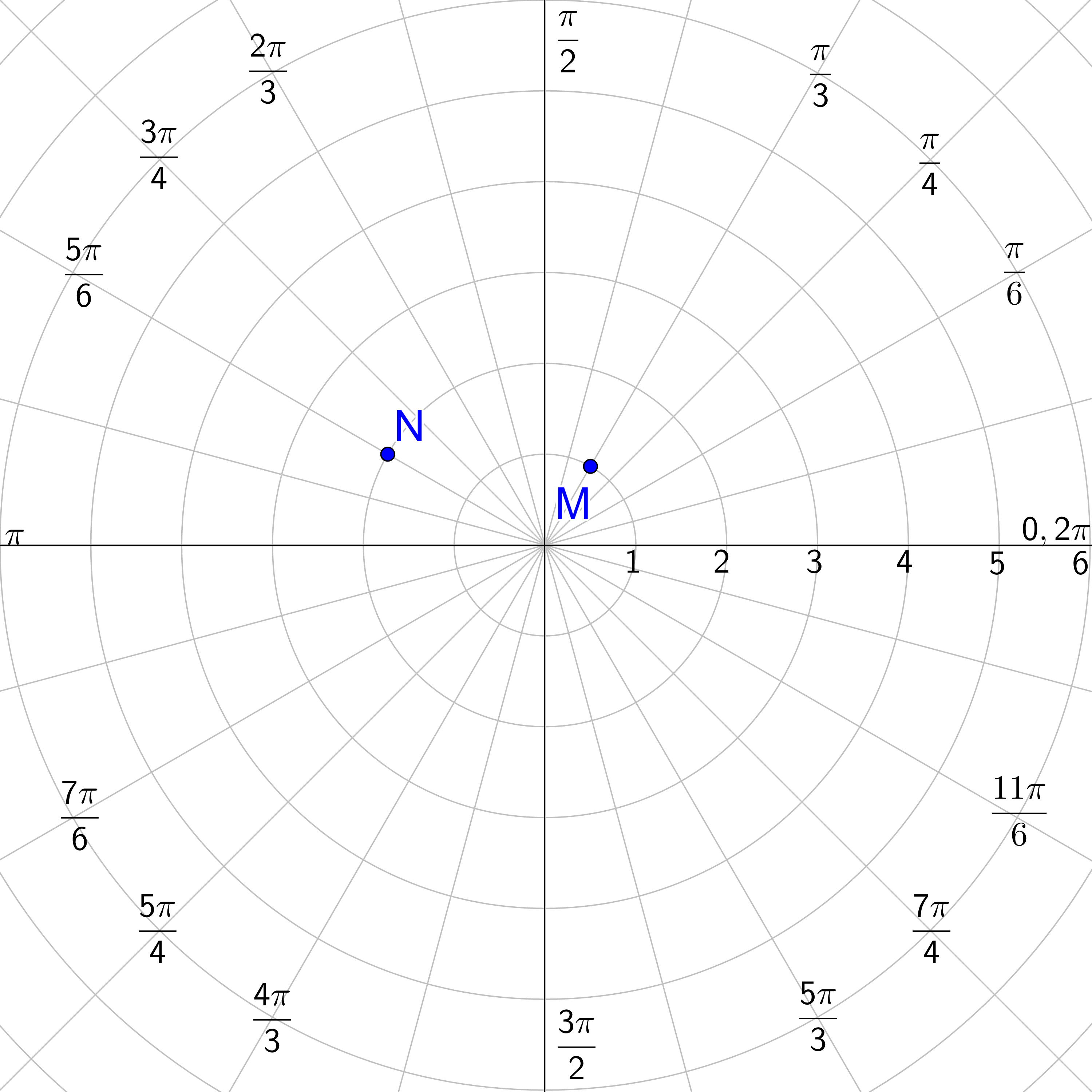
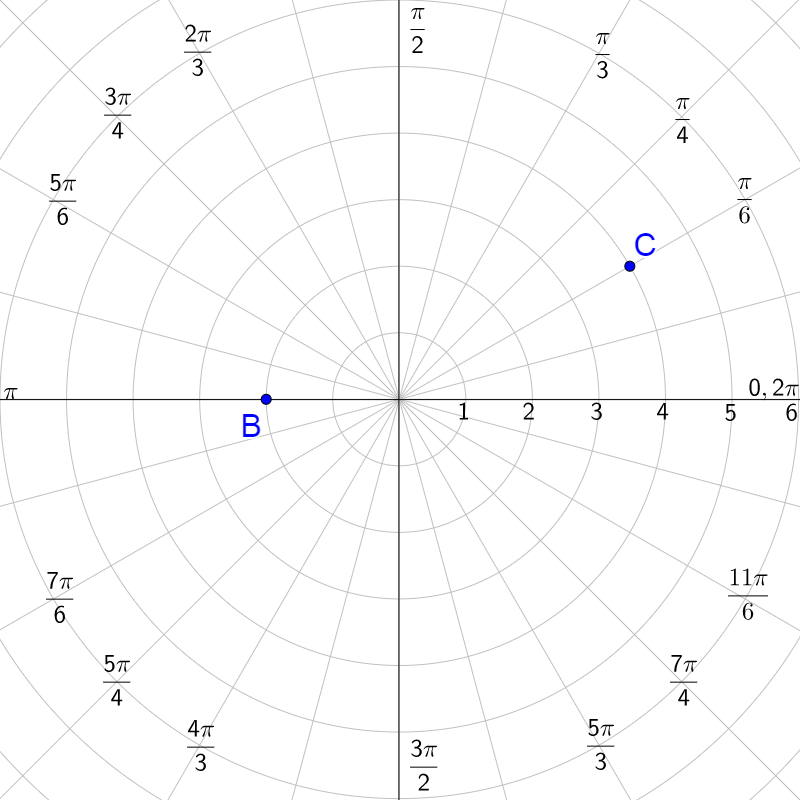
Graph B(2, π) and \(C\left(-4, \frac{7π}{6}\right)\).
Answer
As seen in example 1, there are multiple ways to represent each point in polar coordinates. Different coordinates with the same point when graphed are found simply by adding full circles to the angle. Also, if the r is negative, the point is plotting on the other side of the graph from the given angle. So, by making the r negative and adding π to the angle, the new point would be in the same location as the old point.
Apply one of the following to find a different point that is graphed in the same location.
Add full circles:
\((r, θ) = (r, θ ± 2πn)\)
Add 1/2 circle and go opposite direction:
\((r, θ) = (-r, θ ± (2n + 1)π)\)
Find two other ways to write \(\left(4, \frac{5π}{6}\right)\).
Solution
Add a circle:
$$ \left(4, \frac{5π}{6} + 2π\right) $$
$$ \left(4, \frac{5π}{6} + \frac{12π}{6}\right) $$
$$ \left(4, \frac{17π}{6}\right) $$
Add 1/2 circle and move in the opposite direction:
$$ \left(-4, \frac{5π}{6} + π\right) $$
$$ \left(-4, \frac{5π}{6} + \frac{6π}{6}\right) $$
$$ \left(-4, \frac{11π}{6}\right) $$
Find two other ways to write \(\left(2, \frac{11π}{6}\right)\).
Answer
\(\left(2, \frac{23π}{6}\right)\); \(\left(-2, \frac{17π}{6}\right)\)
Sometimes it is useful to be able to convert between polar and rectangular coordinates. Think of a polar coordinate in the first quadrant. Draw a vertical segment straight down to the x-axis, and then draw a horizontal segment to the pole. Finish by drawing a segment from the pole to the point. This forms a right triangle with the acute angle at the pole being the same measure as the angle in the polar coordinate. See figure 6. The horizontal distance is x-value of the coordinate and the vertical distance is the y-value. If the r and θ are known, the x can be found using cosine and the y can be found using sine.
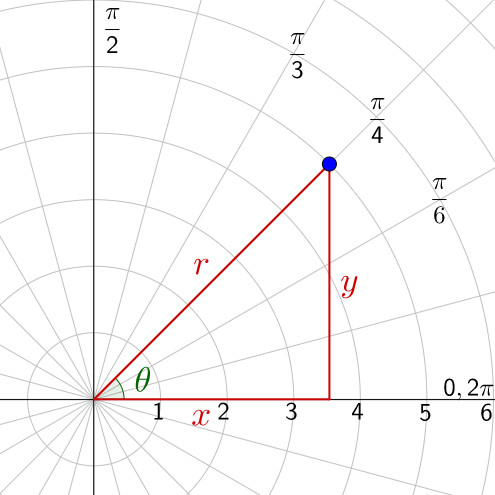
To convert from polar to rectangular coordinates
$$ \begin{align}x &= r \cos θ\\y &= r \sin θ\end{align} $$
To convert from rectangular to polar coordinates
$$ r = \sqrt{x^2 + y^2} $$
$$ \tan θ = \frac{y}{x} $$
Convert \(\left(2, \frac{4π}{3}\right)\) to rectangular coordinates.
Solution
In the polar coordinate \(\left(2, \frac{4π}{3}\right)\), r = 2 and \(θ = \frac{4π}{3}\).
$$ x = r \cos θ $$
$$ x = 2 \cos \frac{4π}{3} $$
$$ x = 2 \left(\frac{1}{2}\right) $$
$$ x = -1 $$
$$ y = r \sin θ $$
$$ y = 2 \sin \frac{4π}{3} $$
$$ y = 2 \left(-\frac{\sqrt{3}}{2}\right) $$
$$ y = -\sqrt{3} $$
The point is \((-1, -\sqrt{3})\).
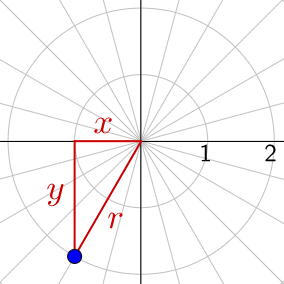
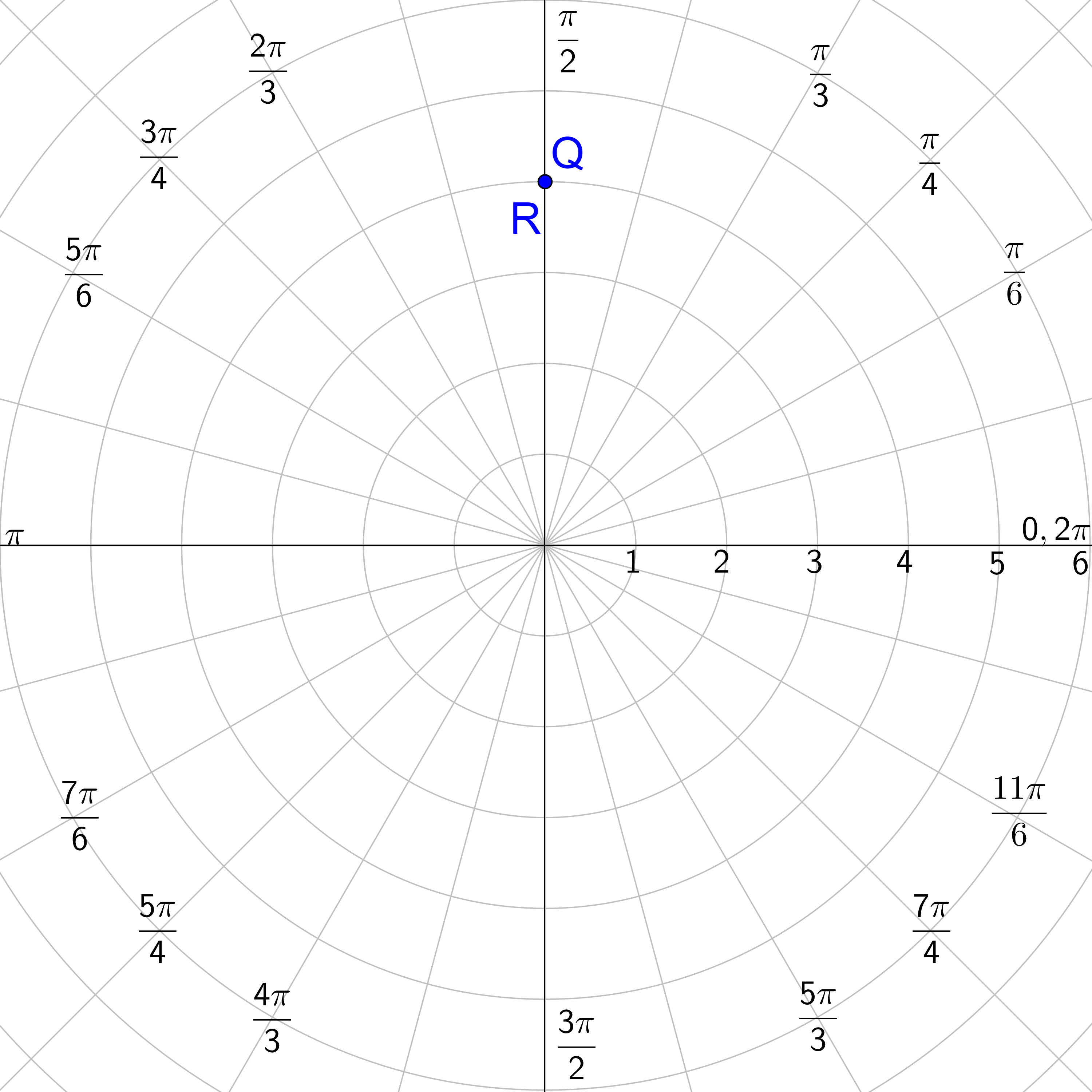
Convert \(\left(0, -4\right)\) to polar coordinates.
Solution
In the rectangular coordinate \(\left(0, -4\right)\), x = 0 and y = −4.
$$ r = \sqrt{x^2 + y^2} $$
$$ r = \sqrt{(0)^2 + (-4)^2} $$
$$ r = \sqrt{16} $$
$$ r = 4 $$
$$ \tan θ = \frac{y}{x} $$
$$ \tan θ = \frac{-4}{0} $$
$$ \tan θ = undefined $$
$$ θ = \frac{π}{2} \text{ or } \frac{3π}{2} $$
The angle in the graph matches \(\frac{3π}{2}\) so use that choice. The point is \(\left(4, \frac{3π}{2}\right)\).
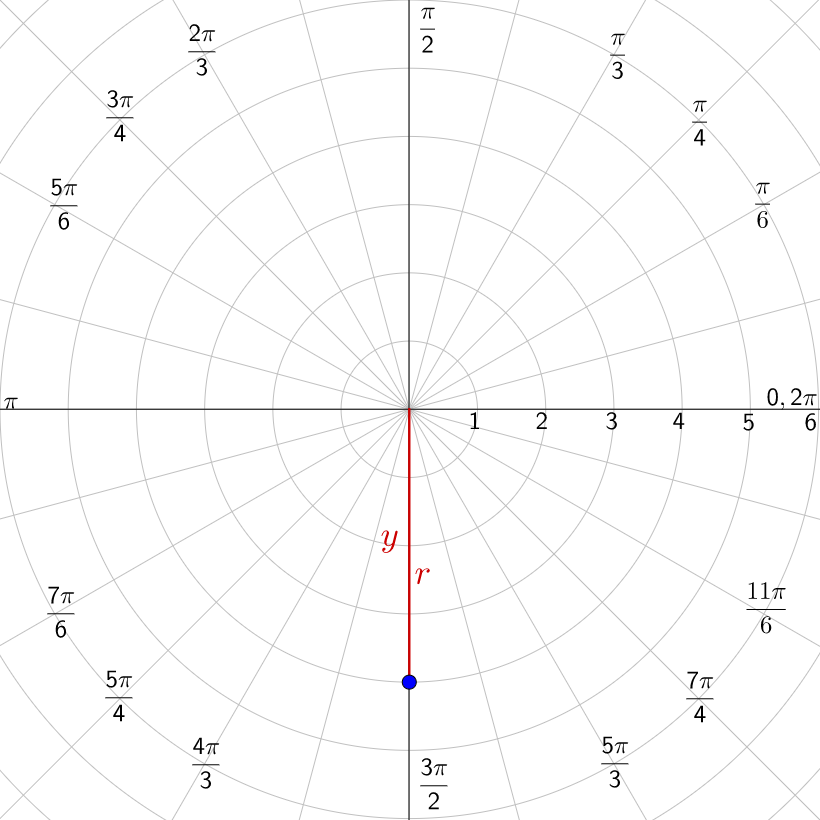
Convert the points to the other coordinate system.
Answer
\(\left(\sqrt{3}, -1\right)\); \(\left(4\sqrt{2}, \frac{7π}{4}\right)\)
To convert equations between polar and rectangular coordinates, use the same substitutions as for the points.
$$ \begin{align}x &= r \cos θ\\y &= r \sin θ\end{align} $$
$$ r = \sqrt{x^2 + y^2} $$
$$ \tan θ = \frac{y}{x} $$
Convert r = 4 to rectangular coordinates.
Solution
Since r is the only variable in the function, substitute \(r = \sqrt{x^2 + y^2}\).
$$ r = 4 $$
$$ \sqrt{x^2 + y^2} = 4 $$
Now square both sides of the equation to get rid of the square root.
$$ x^2 + y^2 = 16 $$
This is a circle centered at (0, 0) with a radius of 4.
Convert \(θ = \frac{2π}{3}\) to rectangular coordinates.
Solution
The only variable is θ. One of the conversion formulas is \(\tan θ = \frac{y}{x}\). To set up the equation for this start by taking the tangent of both sides.
$$ θ = \frac{2π}{3} $$
$$ \tan θ = \tan \frac{2π}{3} $$
Now substitute \(\frac{y}{x}\) for tan θ and evaluate the right-hand side.
$$ \frac{y}{x} = -\sqrt{3} $$
Multiply both sides by x to remove the fraction.
$$ y = -\sqrt{3}x $$
This is a line with y-intercept of 0 and slope of \(-\sqrt{3}\).
Convert r = 3 sec θ to rectangular coordinates.
Solution
None of the conversion formulas have secant, but \(\sec u = \frac{1}{\cos u}\). And cosine is in one of the formulas.
r = 3 sec θ
$$ r = \frac{3}{\cos θ} $$
Multiply both sides by cos θ to get it with the r.
r cos θ = 3
The left-hand side looks like the conversion formula x = r cos θ.
x = 3
This is a vertical line.
Convert r = 2 sin θ to rectangular coordinates.
Solution
This has both r and sin θ, but they are not multiplied with each other. However, they would be if both sides were multiplied by r.
r = 2 sin θ
r2 = 2r sin θ
Now substitute y for r sin θ. Also, since \(r = \sqrt{x^2 + y^2}\), then r2 = x2 + y2.
x2 + y2 = 2y
Gather everything on one side.
x2 + y2 − 2y = 0
Complete the square in y.
x2 + (y2 − 2y + 1) = 0 + 1
x2 + (y − 1)2 = 1
This is a circle centered at (0, 1) with a radius of 1.
Convert r2 = 8r sin θ to rectangular coordinates.
Answer
x2 + (y − 4)2 = 16
(r, θ)
r = distance from pole
θ = angle counterclockwise from the polar axis
Graph by find the line for the angle and moving along that line, the distance, r, from the pole.
Apply one of the following to find a different point that is graphed in the same location.
Add full circles:
\((r, θ) = (r, θ ± 2πn)\)
Add 1/2 circle and go opposite direction:
\((r, θ) = (-r, θ ± (2n + 1)π)\)
To convert from polar to rectangular coordinates
$$ \begin{align}x &= r \cos θ\\y &= r \sin θ\end{align} $$
To convert from rectangular to polar coordinates
$$ r = \sqrt{x^2 + y^2} $$
$$ \tan θ = \frac{y}{x} $$
Helpful videos about this lesson.
