Precalculus by Richard Wright
Precalculus by Richard Wright
For since death came through a man, the resurrection of the dead comes also through a man. 1 Corinthians 15:21 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.5.2, PC.6.7

In physics, projectiles are objects that move only under the influence of gravity. Near the earth, the path of a projectile is a parabola that opens down. While it is possible to write a function to model the motion, it is more useful to have separate functions for the horizontal motion and the vertical motion. Both these functions are based on time.
$$\left\{\begin{align}x &= v_{x0} t\\y &= -9.8 t^2 + v_{y0} t + y_0\end{align}\right.$$
Parametric equations are separate equations for each of the dimensions. The variable in the equations is called the parameter and is often t or θ. To graph parametric equations, make a table of values where you choose values of the parameter and calculate x and y.
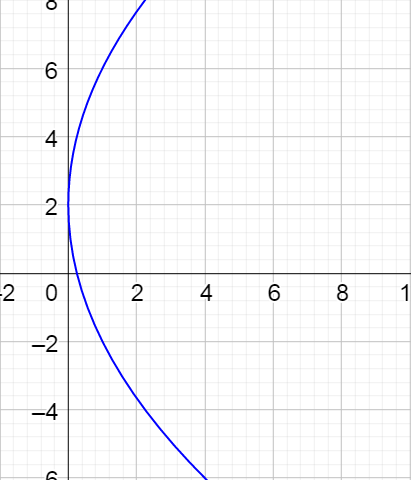
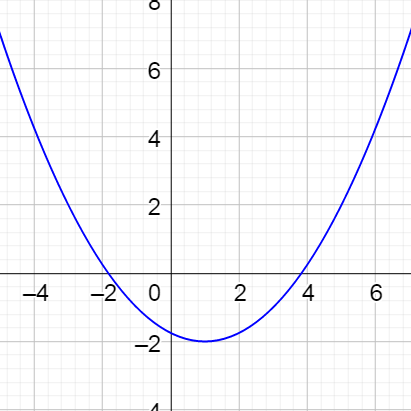
Graph the curve given by
$$\left\{\begin{align}x &= t^2 - 1\\ y &= t - 2\end{align}\right.$$
Solution
Start by making a table by picking values of t and calculating x and y.
| t | −2 | −1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| x | 3 | 0 | −1 | 0 | 3 |
| y | −4 | −3 | −2 | −1 | 0 |
Now graph the points formed from corresponding x and y coordinates.
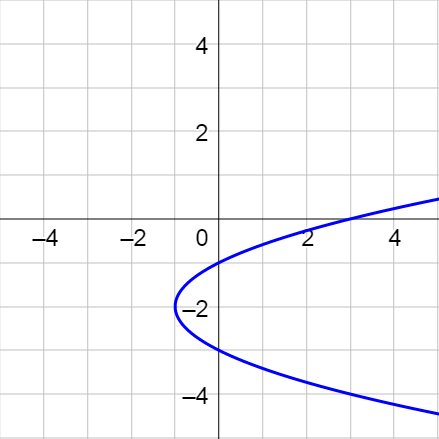
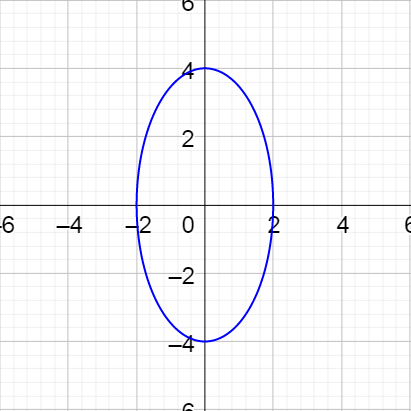
Graph \(\left\{\begin{align}x &= 3\sin θ\\ y &= \cos θ\end{align}\right.\).
Solution
Start by making a table by picking values of θ and calculating x and y.
| θ | 0 | \(\frac{π}{4}\) | \(\frac{π}{2}\) | \(\frac{3π}{4}\) | π | \(\frac{5π}{4}\) | \(\frac{3π}{2}\) | \(\frac{7π}{4}\) | 2π |
|---|---|---|---|---|---|---|---|---|---|
| x | 0 | \(\frac{3\sqrt{2}}{2}\) | 3 | \(\frac{3\sqrt{2}}{2}\) | 0 | \(\frac{-3\sqrt{2}}{2}\) | −3 | \(\frac{-3\sqrt{2}}{2}\) | 0 |
| y | 1 | \(\frac{\sqrt{2}}{2}\) | 0 | \(-\frac{\sqrt{2}}{2}\) | −1 | \(\frac{-\sqrt{2}}{2}\) | 0 | \(-\frac{\sqrt{2}}{2}\) | 1 |
Now graph the points formed from corresponding x and y coordinates.
Graph \(\left\{\begin{align}x &= 2 \sec θ\\y &= \tan θ\end{align}\right.\).
Answer
Parabola
| Horizontal | Vertical |
|---|---|
| \(\left\{\begin{align}x &= pt^2 + h\\y &= 2pt + k\end{align}\right.\) | \(\left\{\begin{align}x &= 2pt + h\\y &= pt^2 + k\end{align}\right.\) |
Ellipse
| Horizontal | Vertical |
|---|---|
| \(\left\{\begin{align}x &= h + a \cos t\\y &= k + b \sin t\end{align}\right.\) | \(\left\{\begin{align}x &= h + b \sin t\\y &= k + a \cos t\end{align}\right.\) |
Hyperbola
| Horizontal | Vertical |
|---|---|
| \(\left\{\begin{align}x &= h + a \sec t\\y &= k + b \tan t\end{align}\right.\) | \(\left\{\begin{align}x &= h + b \tan t\\y &= k + a \sec t\end{align}\right.\) |
Write a set of parametric equations for a vertical ellipse with center (2, 3), major axis length 10, and minor axis length of 8.
Solution
The equations for a vertical ellipse are \(\left\{\begin{align}x &= h + b \sin t\\y &= k + a \cos t\end{align}\right.\). The center is (h, k) = (2, 3) so h = 2 and k = 3. The variable a is half the major axis which is 10, so a = 5. b is half the minor axis length which is 8, so b = 4. Now fill in the equations.
$$\left\{\begin{align}x &= h + b \sin t\\y &= k + a \cos t\end{align}\right.$$
$$\left\{\begin{align}x &= 2 + 4 \sin t\\y &= 3 + 5 \cos t\end{align}\right.$$
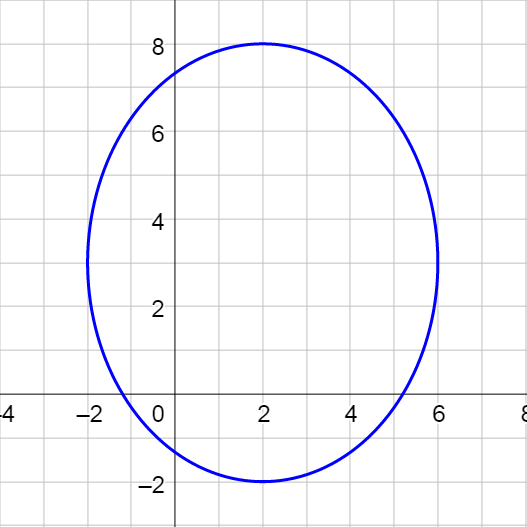
Write a set of parametric equations for y2 = 4x − 4.
Solution
This is a parabola, so use the equation for a horizontal parabola.
$$\left\{\begin{align}x &= pt^2 + h\\y &= 2pt + k\end{align}\right.$$
To use these p, h, and k need to be known, so put the equation in standard form.
$$y^2 = 4x - 4$$
$$y^2 = 4(x - 1)$$
When compared to (y − k)2 = 4p(x − h), we find that p = 1, h = 1, and k = 0. Now fill in the parametric equations.
$$\left\{\begin{align}x &= pt^2 + h\\y &= 2pt + k\end{align}\right.$$
$$\left\{\begin{align}x &= t^2 + 1\\y &= 2t\end{align}\right.$$
Another way is to choose something to equal t. Since to solve y2 = 4(x − 1) for y, the square root would have to be taken, it would be convenient to let t2 = x − 1. Solve this for x to get
$$x = t^2 + 1$$
Substitute this for x in the equation to get
$$y^2 = 4(t^2 + 1 - 1)$$
Then solve for y.
$$y^2 = 4t^2$$
$$y = 2t$$
So the parametric equations are
$$\left\{\begin{align}x &= t^2 + 1\\y &= 2t\end{align}\right.$$
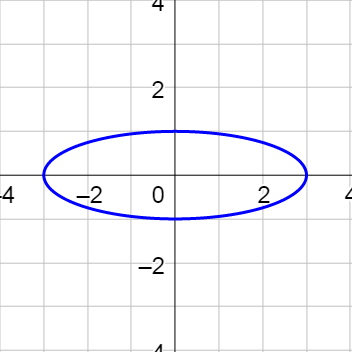
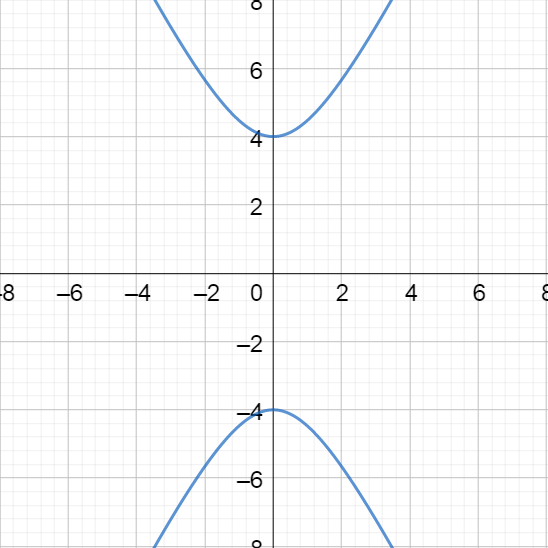
Write a set of parametric equations for \(\frac{x^2}{4} + \frac{y^2}{16} = 1\).
Answer
\(\left\{\begin{align}x &= 2 \sin θ\\y &= 4 \cos θ\end{align}\right.\)
It is possible to change parametric equations into regular functions by eliminating the parameter. To do this, solve one of the parametric equations for t and substitute the expression into the other equation. If the equations contain sine and cosine, or tangent and secant, it might be easier to solve each equation for the trigonometric function and use a Pythagorean Identity such as sin2 θ + cos2 θ = 1 or 1 + tan2 θ = sec2 θ.
If the equations do not have trigonometric functions.
If the equations do have trigonometric functions.
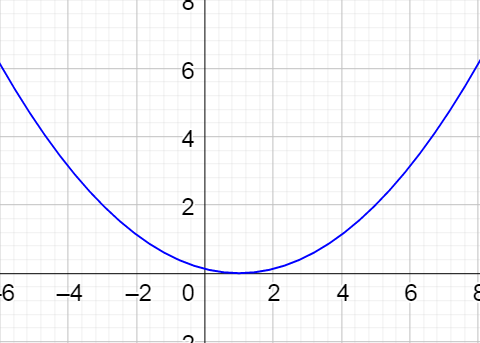
Eliminate the parameter in \(\left\{\begin{align}x &= t^2 - 1\\y &= 3t\end{align}\right.\).
Solution
Since these do not have trigonometric functions, start by solving one equation for t.
$$x = t^2 - 1$$
$$x + 1 = t^2$$
$$±\sqrt{x + 1} = t$$
Now substitute this into the other equation.
$$y = 3t$$
$$y = 3 \left(± \sqrt{x + 1}\right)$$
Eliminate the ± by squaring both sides.
$$y^2 = 9(x + 1)$$
This is a horizontal parabola.
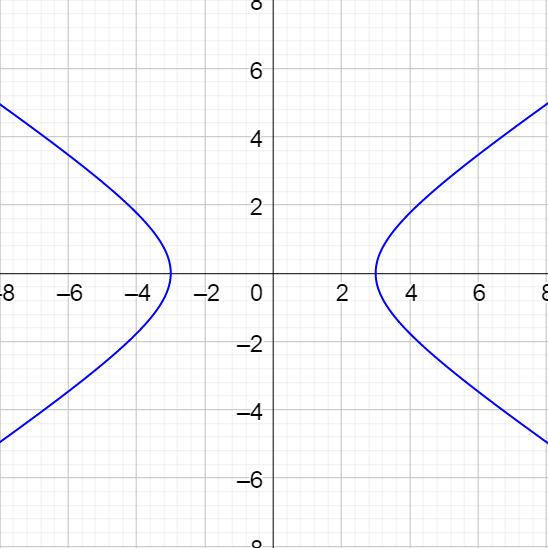
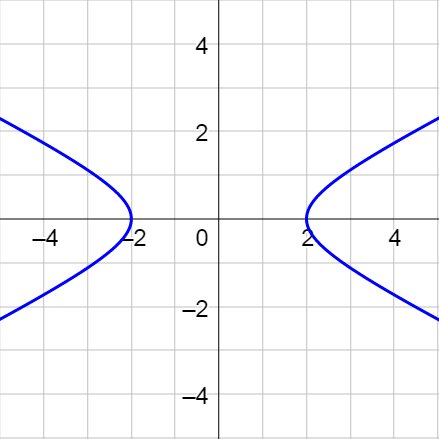
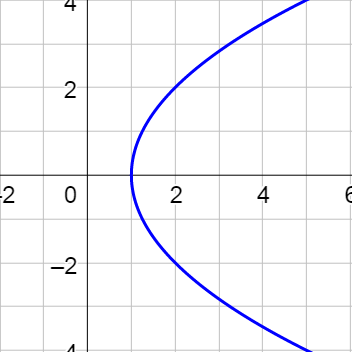
Eliminate the parameter in \(\left\{\begin{align}x &= 2 \tan θ\\y &= 4 \sec θ\end{align}\right.\).
Solution
Since these do have trigonometric functions, it will be easier to solve the equations for the trig functions.
$$\left\{\begin{align}x &= 2 \tan θ\\y &= 4 \sec θ\end{align}\right.$$
$$\left\{\begin{align}\frac{x}{2} &= \tan θ\\ \frac{y}{4} &= \sec θ\end{align}\right.$$
An identity that relates secant and tangent is
$$ 1 + \tan^2 θ = \sec^2 θ $$
$$1 + \left(\frac{x}{2}\right)^2 = \left(\frac{y}{4}\right)^2$$
$$1 + \frac{x^2}{4} = \frac{y^2}{16}$$
Rearrange the equation to put it in standard form.
$$\frac{y^2}{16} - \frac{x^2}{4} = 1$$
This is a vertical hyperbola.
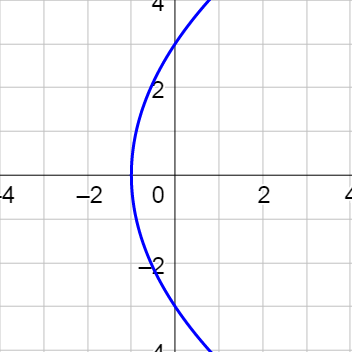
Eliminate the parameter.
Answers
\(y = x^2 - 4x + 4\), \(\frac{x^2}{4} + \frac{y^2}{9} = 1\)
Parabola
| Horizontal | Vertical |
|---|---|
| \(\left\{\begin{align}x &= pt^2 + h\\y &= 2pt + k\end{align}\right.\) | \(\left\{\begin{align}x &= 2pt + h\\y &= pt^2 + k\end{align}\right.\) |
Ellipse
| Horizontal | Vertical |
|---|---|
| \(\left\{\begin{align}x &= h + a \cos t\\y &= k + b \sin t\end{align}\right.\) | \(\left\{\begin{align}x &= h + b \sin t\\y &= k + a \cos t\end{align}\right.\) |
Hyperbola
| Horizontal | Vertical |
|---|---|
| \(\left\{\begin{align}x &= h + a \sec t\\y &= k + b \tan t\end{align}\right.\) | \(\left\{\begin{align}x &= h + b \tan t\\y &= k + a \sec t\end{align}\right.\) |
If the equations do not have trigonometric functions.
If the equations do have trigonometric functions.
Helpful videos about this lesson.